考虑滚珠尺寸误差时滚珠螺旋副的受力和寿命分析

,

(华东理工大学机械与动力工程学院,上海 200237)

考虑滚珠尺寸误差时滚珠螺旋副的受力和寿命分析

甄妮,安琦

(华东理工大学机械与动力工程学院,上海200237)

以外循环式滚珠螺旋副为研究对象,通过力学分析建立了一种考虑滚珠尺寸误差、计算每个滚珠受力及滚珠螺旋副寿命的计算模型。结合一个具体的算例,研究了只存在一个滚珠误差、所有滚珠存在随机性误差两种情况下尺寸误差对滚珠受力情况及疲劳寿命的影响,绘制了滚珠最大接触应力曲线,计算了滚珠螺旋副的疲劳寿命。研究结果表明:提高滚珠加工精度,滚珠螺旋副的寿命也随之增加。

滚珠螺旋副; 尺寸误差; 力学分析; 疲劳寿命

滚珠螺旋副是在螺杆齿槽和螺旋套齿槽之间设置适量滚珠作为中间传动体的螺旋传动方式。与滑动螺旋副相比,滚珠螺旋副具有较高的传动效率和较长的使用寿命。滚珠在加工过程中存在尺寸误差,而目前对滚珠螺旋副进行力学分析及寿命计算中大多没有考虑这一因素。

黄琴等[1]对封闭槽螺母滚动螺旋副的弹性接触变形进行分析与推导,建立的模型忽略螺旋角、载荷分布不均的影响,推导出在轴向载荷作用下,滚珠螺旋副的轴向弹性位移量的计算公式和简化公式。姜洪奎[2]建立了滚珠丝杠副的力学模型,并利用有限元方法验证力学模型,分析了螺旋升角、接触角对滚珠丝杠副力学性能的影响。翁健光等[3]以赫兹接触理论为基础,假设滚珠受力情况相同,建立滚珠丝杆副的接触变形与刚度的数学模型。战小明[4]在Pro-E中建立了滚珠丝杆模型,并导入仿真软件进行动力学分析,得到变形与受力的关系。赵国平等[5]以短时高过载精密滚珠丝杆副为研究对象,结合赫兹接触理论和弹性变形理论,假设轴向载荷均匀地分配给每个滚珠,得到高承载工况下单螺母滚珠丝杆副的接触变形的理论计算方法,结果表明丝杆副塑性变形量远小于弹性变形量。王琦等[6]对滚珠丝杆空间运动过程进行了分析,假设滚珠均匀受载,利用Matlab分析了螺旋升角、接触角、载荷对滚珠螺旋接触变形和接触刚度的影响。张佐营[7]假设滚珠受力相同,得到滚珠螺旋副轴向载荷与变形关系,分析了只有一个滚珠存在误差时的各滚珠受力情况。Mei等[8]研究了误差对滚珠螺旋副载荷分布的影响,认为负误差使滚珠受载减小,当负误差达到某一值时,滚珠与齿槽不接触,不存在接触受力;正误差使滚珠受载增加。Xu等[9]进一步进行研究,提出一种改进计算模型,降低力的突变程度,并分析了螺距对载荷分布的影响。Shimoda[10]分析了载荷分布和制造误差对滚动螺旋副刚度的影响,尺寸误差使各滚珠接触变形发生变化,而滚珠螺旋副的刚度与最大接触变形有关。Bertolaso等[11]通过理论分析、实验、数值分析3种方法研究了滚动螺旋副载荷分布情况,并且分析了接触角对受力的影响。

通过以上文献分析可知,目前研究中构建的力学模型,大多是假设滚珠不存在误差,每个滚珠受力相同,但在实际加工过程中,滚珠一定存在误差,从而使每个滚珠受力不同,这将对使用寿命产生影响。本文通过对滚珠螺旋副的力学分析,在考虑滚珠尺寸误差的基础上,构建能对每一个滚珠进行受力计算的力学模型,利用数值模拟的方法进行计算研究,探寻滚珠尺寸误差对滚珠螺旋副受力及疲劳寿命的影响规律。

1 力学模型的构建

1.1滚珠螺旋副整体受力分析

本文对滚珠螺旋副进行力学建模时首先引入如下假设:

(1) 滚珠螺旋副只受到轴向载荷的作用;

(2) 滚珠直径存在误差,但滚珠只发生尺寸误差,外形仍保持为球形;

(3) 滚珠螺旋副的受力均在弹性变形范围;

(4) 滚珠螺旋副转速较低,忽略离心力和陀螺力矩。

滚珠螺旋副结构如图1(a)所示。工作过程中,螺旋套固定在机座上,螺杆转动,加在螺杆上的轴向力为Fa(包含螺杆自重),滚珠与螺杆及螺旋套发生接触产生弹性变形,螺杆产生轴向位移δa,nj为螺杆旋转速度。对第i个滚珠受力分析如图1(b)所示,滚珠与螺杆的接触力为Pji,滚珠与螺旋套的接触力Poi。

螺杆轴向平衡方程如下:

(1)

其中:z为滚珠数;α为螺旋升角;βi为第i个滚珠的接触角。

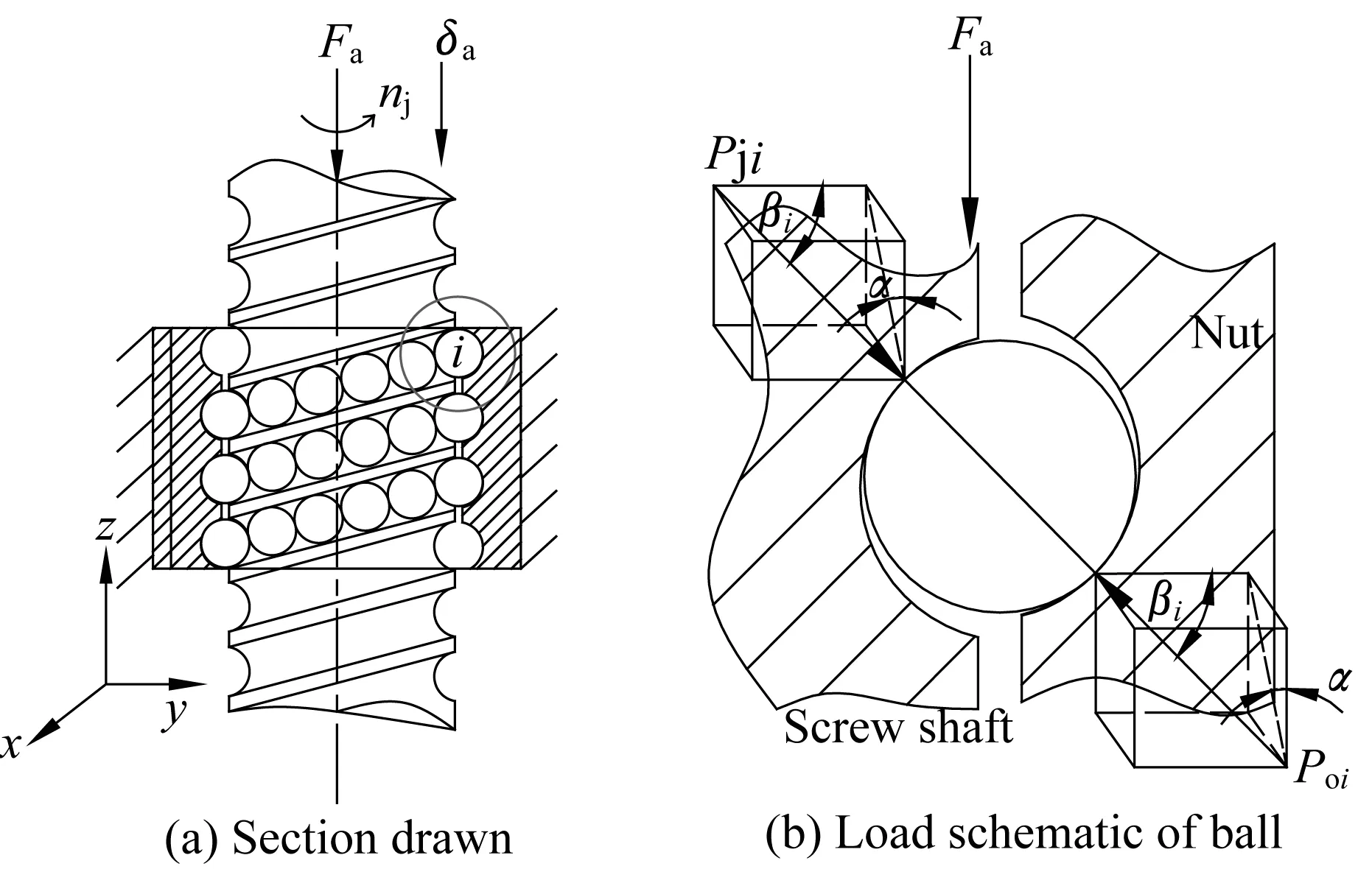
图1 轴向力作用下滚珠螺旋副的受力示意图Fig.1 Ball screw load schematic with axial load

1.2滚珠受力及变形分析

两弹性体接触未发生变形时为点接触(图2实线部分),受力发生赫兹接触,接触点变成一个平面(图2虚线部分),两弹性体均产生趋近量,分别为δ1、δ2。由图2可知,两弹性体间发生赫兹接触产生赫兹接触变形量δ,δ=δ1+δ2。

图2 两弹性体发生赫兹接触Fig.2 Hertz contact deformation

对第i个滚珠进行分析。如图3所示,不考虑滚珠离心力时,滚珠与螺杆齿槽和螺旋套齿槽的接触角相同,螺杆齿槽曲率中心Oj和螺旋套齿槽曲率中心Oo与滚珠球心OD共线,此时接触点为E和F,β0为未变形时的初始接触角,螺旋套齿槽曲率中心和螺杆齿槽曲率中心间距离为A。

A=ro+rj-D

(2)

其中:ro为螺旋套齿槽曲率半径;rj为螺杆齿槽曲率半径;D为滚珠直径。

图3 施加载荷后的变形关系Fig.3 Contact deformation with axial load

(3)

滚珠与齿槽间赫兹接触变形量δni由两部分组成,一部分为滚珠与螺杆齿槽间接触变形量δni,j,另一部分为滚珠与螺旋套齿槽接触变形δni,o。则δni可表示为

(4)

由几何关系可得接触角βi为

(5)

由赫兹接触理论,Pji与δni的关系为

(6)

(7)

其中:a、b为螺杆及螺旋套上的接触椭圆长半轴和短半轴。

将式(4)～(6)带入式(1)得到

(8)

1.3考虑滚珠误差的计算模型

考虑滚珠尺寸误差时,每个滚珠的受力情况发生改变。设Ti表示第i个滚珠的尺寸误差,尺寸误差为正误差时Ti为正值;尺寸误差为负误差时Ti为负值。由于每个滚珠的直径不同,产生的接触变形不同,受力也不同,所以当齿槽与部分滚珠发生接触时,可能有一些滚珠由于尺寸偏小而未与齿槽发生接触,不存在接触载荷。

对第i个滚珠进行分析,如图4所示。

若δni+Ti>0,说明螺杆齿槽与螺旋套齿槽之间趋近量大于滚珠尺寸误差,此时滚珠与螺杆、螺旋套均接触,滚珠受载,但趋近量发生变化,则考虑滚珠尺寸误差时的接触变形量(δni)T可表示为(δni)T=δni+Ti;若δni+Ti<0,说明螺杆齿槽与螺旋套齿槽之间趋近量小于滚珠尺寸误差,此时滚珠与螺杆、螺旋套均不接触,滚珠不受载,(δni)T=0。

考虑滚珠尺寸误差时,相对于不考虑滚珠尺寸误差的求解过程,需对滚珠是否产生接触变形、接触

图4 考虑滚珠尺寸误差的接触变形Fig.4 Contact deformation considering dimension errors

变形为多少进行判断,计算过程如下:

(1) 给定轴向载荷Fa、滚珠螺旋副结构参数、滚珠误差序列Ti、计算精度ERR,迭代数值Δδa;

(2) 给轴向位移δa赋初值;

(3) 利用式(4)和式(5)计算螺杆齿槽与螺旋套齿槽间接触变形δni及接触角βi;

(4) 对滚珠是否产生接触变形进行判断,若δni+Ti<0,则滚珠不受载,(δni)T=0;若δni+Ti>0,则滚珠受载,(δni)T=δni+Ti,将接触变形带入式(6)和式(7)计算Pji和σmax,i;

利用Matlab计算上述过程,程序流程见图5。

1.4疲劳寿命计算方法

材料疲劳曲线的指数方程:

(9)

其中:N为疲劳寿命循环次数;σ为N对应的接触应力;σ0为循环基数;N0为对应的接触疲劳极限。当硬度 HRC=60时,σ0=2 450 N/mm2,N0=108,当钢受接触应力时,m=6。

对第i个滚珠进行运动分析如图6所示,其中D0为滚珠中心圆直径,DF为F点中心圆直径。

螺旋套固定不动,螺杆以转速nj旋转,接触点E为滚珠运动瞬心,vj为接触点F的线速度,vD为滚珠中心线速度,由图6可知速度关系如下:

vD=vj/2

(10)

图5 Matlab计算流程图Fig.5 Matlab calculation flow chart

图6 滚珠运动分析Fig.6 Kinematics analysis of ball

由图6中几何关系及式(10)计算滚珠绕螺杆公转转速nDg为

(11)

滚珠绕螺杆公转的同时自转,设其自转转速为nDz,滚珠与齿槽间无滑动,在接触点F上螺杆和滚珠的相对线速度相同,则滚珠自转转速nDz为

1.2.1 医务工作者职业幸福感调查问卷 该问卷由李桂华等[6]编制，包含5个维度24个条目：身心健康状况(6个条目)；价值/能力体现(6个条目)；社会支持(5个条目)；工作环境(4个条目)；经济收入(3个条目)。采用Likert 5级评分法：1分为完全不符合，2分为基本不符合，3分为不确定，4分为基本符合，5分为完全符合。总分120分，分数越高表示职业幸福感越强。

(12)

滚珠每自转一圈,滚珠上某一定点接触齿槽两次,则通过式(9)可以计算出疲劳寿命对应的循环次

数,进而计算出以小时为单位的疲劳寿命t为

(13)

2 算例分析

2.1参数设置

选用3210-4型滚珠螺旋副进行分析,其尺寸及性能参数见表1,其中c为工作圈数。滚珠材料为轴承钢GCr15。

表1 滚珠螺旋副性能参数

表1中工作圈数存在半圈是因为滚珠螺旋副中有部分滚珠在返回装置中,不参与工作,不承受轴向载荷。本算例中共48个滚珠,工作圈数2.5,则40个滚珠在滚道中,承受轴向载荷,8个滚珠在返回装置中,不承受轴向载荷。以第1个承受轴向载荷的滚珠为1号滚珠,41到48号滚珠不承受轴向载荷。

不考虑滚珠尺寸误差时,各滚珠受力相同,按照第1.4节中式(13)的计算方法,利用Matlab计算各滚珠受力。设轴向载荷为5 kN,计算得到滚珠与螺杆间最大接触应力为1 655 MPa,根据式(13)计算寿命:

t=

2.2只有一个滚珠存在误差

2.2.1 只有一个滚珠存在负误差 设轴向载荷为5 kN,假设只有第3个滚珠出现3.0 μm的负误差,各滚珠与螺杆、螺旋套接触时的最大接触应力如图7所示。由图7可知,当第3个滚珠存在负误差时,这个滚珠受到的应力减小,齿槽中其他滚珠受到的应力随之略微增大,以保证与轴向力平衡。返回装置中滚珠不承受轴向力。

由于一个滚珠存在3.0 μm负误差使正常滚珠受力增大,对寿命产生影响,此时滚珠与螺杆间最大接触应力为1 665 MPa,根据式(13)计算寿命:

t=

当负误差为0～3.0 μm时,齿槽中正常滚珠(齿槽中除3号滚珠以外)和齿槽中误差滚珠(3号滚珠)最大接触应力如图8所示。由图8可知,齿槽中随着一个滚珠负误差的增大,误差滚珠受到的应力减小,而其他正常滚珠受到的应力逐渐增大,而应力增大会导致寿命降低。所以随着负误差的增大,滚珠受到的最大应力增大,寿命降低。

图7 第3个滚珠存在负误差时各滚珠最大接触应力Fig.7 Maximum stress of every ball when No.3 ball has negative error

2.2.2 只有一个滚珠存在正误差 设轴向载荷为5 kN,假设只有第3个滚珠出现3.0 μm的正误差,各滚珠与螺杆、螺旋套接触时的最大接触应力如图9所示。由图9可知,当第3个滚珠存在正误差时,则这个滚珠受到的应力增大,齿槽中其他滚珠受到的应力随之略微减小,以保证与轴向力平衡。返回装置中滚珠不承受轴向力。

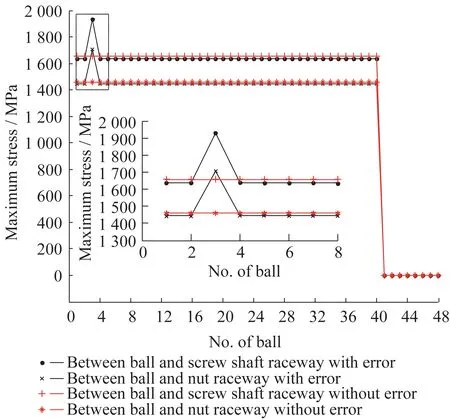
图9 第3个滚珠存在正误差时各滚珠最大接触应力Fig.9 Maximum stress of every ball when No.3 ball has positive error

由于一个滚珠存在3.0 μm正误差使误差滚珠受力增大,对寿命产生影响,此时滚珠与螺杆间最大接触应力为1 931 MPa,根据式(13)计算寿命:

t=

当正误差范围为0～3.0 μm时,齿槽中正常滚珠(齿槽中除3号滚珠以外)和齿槽中误差滚珠(3号滚珠)最大接触应力如图10所示。由图10可知,齿槽中随着一个滚珠正误差的增大,正常滚珠受到的应力逐渐减小,误差滚珠受到的应力增大,而应力增大会导致寿命降低。所以随着正误差的增大,滚珠受到的最大应力增大,寿命降低。综上,齿槽中任意滚珠存在误差时,其接触载荷发生突变,影响接触应力分布,并使齿槽中其他滚珠受力发生变化。存在负误差时,正常滚珠应力增大寿命减小;存在正误差时,误差滚珠应力增大寿命减小,且正误差对寿命的影响较大,返回装置中的滚珠不受载。

图10 正误差与接触应力关系Fig.10 Relationship between positive error and maximum stress

2.3所有滚珠存在随机性误差

实际加工中每个滚珠都可能存在误差,误差具有随机性,本文在分析时利用Matlab中的函数随机生成一组滚珠直径误差,模拟实际滚珠的误差分布。由于各滚珠误差存在随机性,每个滚珠的误差不同,受力和寿命也不同。返回装置中的滚珠不承受轴向载荷。

当滚珠误差范围为±3.0 μm时,随机生成的各滚珠尺寸误差值如图11所示,滚珠不断转动的过程中,参与受载的滚珠不断变化,每个滚珠的受力也不断变化。设轴向载荷为5 kN,图11为滚珠分别转过1、2、3圈时各滚珠与螺杆、螺旋套间最大接触应力。

由图11可知,在齿槽中受力最大的滚珠始终是有最大正误差的滚珠。每个滚珠转动一圈的过程都会经历在齿槽中承受载荷及在返回装置中不承受载荷,22号滚珠存在最大的正误差,工作过程中受力最大。图12示出了22号滚珠完成一个循环的最大接触应力变化。由图12可知,最大接触应力的峰值出现在滚珠转过292.5°,滚珠与螺杆间的最大接触应力为1 945 MPa,根据式(13)计算寿命:

t=

由计算结果可知,相对于无误差情况,考虑滚珠尺寸误差时,疲劳寿命明显降低。

图11 一个循环中各个滚珠最大接触应力Fig.11 Maximum stress of every ball in a cycle

滚珠误差范围为±2.0 μm时,随机生成的各滚珠尺寸误差如图13所示,各滚珠与螺杆齿槽、螺旋套齿槽间最大接触应力如图13所示,与误差范围在±3.0 μm相比,最大接触应力的变化范围缩小。

由图13可知,39号滚珠存在最大正误差,其从初始位置经过一个循环回到初始位置的最大接触应力变化如图14所示。最大接触应力的峰值出现在滚珠转过1 057.5°,滚珠与螺杆间的最大接触应力为1 864 MPa,根据式(13)计算寿命:

t=

计算结果表明,当误差范围在±2.0 μm时,与误差范围在±3.0 μm相比,疲劳寿命增加。

图12 22号滚珠经过一个循环时在各位置的最大接触应力Fig.12 Maximum stress of No.22 ball at each location in a cycle

图13 误差范围为±2.0 μm时各滚珠接触应力Fig.13 Maximum stress of every ball when error range is ±2.0 μm

图14 39号滚珠经过一个循环时在各位置的最大接触应力Fig.14 Maximum stress of No.39 at each location ball in a cycle

根据机械设计手册[13],滚珠加工精度G有10个等级,其对应的误差见表2,按照以上分析过程,计算不同加工精度下滚珠螺旋副寿命如图15所示。

表2 各精度下滚珠尺寸误差

由图15可知,当精度越高时,滚珠尺寸误差范围越小,滚珠螺旋副寿命越长。因此在设计滚珠螺旋副时,可以根据本文的算法思想,由滚珠螺旋副寿命要求来选择精度,然后按照本文的计算方法得到每一个滚珠的接触应力,从而计算出滚珠螺旋副寿命,再与疲劳寿命要求进行对比后确认所选的精度是否可以满足要求,这对实际应用很有意义。

图15 不同加工精度的滚珠螺旋副疲劳寿命Fig.15 Fatigue life of ball screw under different accuracy

3 结 论

(1) 通过对滚珠螺旋副进行力学分析,研究了滚珠在工作过程中受力计算的力学模型,建立了能够在考虑滚珠尺寸误差的情况下计算每一个滚珠受力的计算方法,结合滚珠螺旋副滚珠的运动学分析及疲劳寿命计算方法,实现了在考虑滚珠尺寸误差条件下对滚珠螺旋副滚珠疲劳寿命的计算。

(2) 结合一具体算例,计算研究了只有一个滚珠存在尺寸误差时各滚珠受力及寿命。当只有一个滚珠存在正误差时,该滚珠的受力将会明显增大,并且随误差的增加而增加,其他滚珠的受力将会减小,但由于该滚珠的受力增加,从而使得螺旋副的寿命降低;当只有一个滚珠存在负误差时,该滚珠的受力将会减小,其他滚珠的受力将会增大,也会导致螺旋副疲劳寿命的降低。

(3) 结合算例研究了滚珠存在随机性误差时各个滚珠受力及寿命。随机性误差使每个滚珠受力都不同,同时在滚珠不断转动的过程中,参与受载的滚珠不断变化,每个滚珠的受力也不断变化,但最大接触应力出现在有最大正误差的滚珠上,同时这个滚珠的寿命最短,而这个滚珠的寿命决定滚珠螺旋副的寿命。

(4) 计算了随机误差分别在±3.0 μm和±2.0 μm范围内各个滚珠的受力情况及滚珠螺旋副的寿命,结果表明缩小误差范围可以提高滚珠螺旋副寿命。在此基础上得到滚珠加工精度与滚珠螺旋副寿命的关系曲线,该曲线表明随着加工精度的提高,疲劳寿命增加,为实际工程中保证滚珠螺旋副的寿命提供了有益的参考。

[1] 黄勤,周元康.封闭槽螺母滚动螺旋副弹性变形问题的探讨[J].机械设计,2002,19(12):43-45.

[2] 姜洪奎.大导程滚珠丝杠副动力学性能及加工方法研究[D].济南:山东大学,2007.

[3] 翁健光,袁军堂,汪振华,等.滚珠丝杠副静力学特性分析[J].制造技术与机床,2012(11):127-130.

[4] 战晓明.滚珠丝杆副动态结构分析及其动力学仿真[D].南京:东南大学,2010.

[5] 赵国平,范元勋,罗相银,等.高过载精密滚珠丝杠副弹塑性接触变形研究[J].南京理工大学学报(自然科学版),2014,38(2):192-198.

[6] 王琦,赵飞,张驰,等.滚珠丝杠传动特性与刚度特性研究[J].机械制造,2015,53(9):24-28.

[7] 张佐营.高速滚珠丝杠副动力学性能分析及其实验研究[D].济南:山东大学,2008.

[8] MEI Xuesong,TSUTSUMI M,TAO Tao,etal.Study on the load distribution of ball screws with errors[J].Mechanism and Machine Theory,2003,38(11):1257-1269.

[9] XU Sheng,YAO Zhenqiang,SUN Yaofei,etal.Load distribution of ball screw with consideration of contact angle variation and geometry errors[C]//Proceeding of the ASME International Mechanical Engineering Congress and Exposition.New York,USA:AMER SOC Mechanical Engineers,2014:V02BT02A024.

[10] SHIMODA H.Stiffness analysis of ball screw-Influence of load distribution and manufacturing error[J].International Journal of the Japan Society for Precision Engineering,1999,33(3):168-172.

[11] BERTOLASO R,CHEIKH M,BARRANGER Y,etal.Experimental and numerical study of the load distribution in a ball-screw system[J].Journal of Mechanical Science and Technology [J].2014,28(4):1411-1420.

[12] 程光仁,施祖康,张超鹏.滚珠螺旋传动设计基础[M].北京:机械工业出版社,1987:72-86.

[13] 闻邦椿.机械设计手册-轴承[M].北京:机械工业出版社,2014:307-308.

AnalysisofStressandFatigueLifeofBallScrewwithConsideringDimensionErrorsofBalls

ZHENNi,ANQi

(SchoolofMechanicalandPowerEngineering,EastChinaUniversityofScienceandTechnology,Shanghai200237,China)

Taking ball screw with outer cycling device as the research object,by means of mechanics analysis,a calculation model,which can calculate the contact stress of every ball and the fatigue life of ball screw with considering dimension errors,is put forward.With a concrete example,the influences of the dimension error on the contact stress and fatigue life of two situations,the first one is only one ball has dimension error and the second one is that every ball has random dimension error,are studied.The maximum contact stress of balls is mapped,and the fatigue life of ball screw is calculated.Meanwhile the influences of machining accuracy on the ball screw’s fatigue life have been analyzed.The fatigue life of ball screw increases as the machining accuracy increases.

ball screw; dimension errors; mechanics analysis; fatigue life

TH133.33

A

1006-3080(2017)05-0724-09

10.14135/j.cnki.1006-3080.2017.05.019

2016-12-27

上海市设计学 IV 类高峰学科项目(DA17014)

甄 妮(1992-),女,哈尔滨人,硕士生,研究方向为工程摩擦学。E-mail:1306673980@qq.com

安 琦,E-mail:anqi@ecust.edu.cn