基于模态分离算法的管道焊缝缺陷模拟
,
(华东理工大学承压系统与安全教育部重点实验室,上海 200237)
基于模态分离算法的管道焊缝缺陷模拟
叶梦雅,胡明慧
(华东理工大学承压系统与安全教育部重点实验室,上海200237)
在温度、压力、介质腐蚀、振动等影响下,在役工业管道焊缝内部的小缺陷易发展成裂纹,对管道安全运行产生危害。在模态对称分离算法检测单焊缝管道缺陷的基础上,基于L(0,2)模态导波进行数值模拟,分别以前焊缝缺陷对称面、弯管对称面为纵坐标建立新的笛卡尔直角坐标系,根据对称原理,易于提取缺陷特征。模拟结果表明,非对称幅值与裂纹深度呈指数函数关系,该方法可以实现双焊缝和弯管焊缝缺陷的识别和定量。
超声导波; 焊缝缺陷; 模态分离;L(0,2)模态; 模拟
管道在石油、化工和天然气等领域应用广泛,工业管道大多采用弯管与直管焊接而成,为保证管道的安全运行,需对其定期检测。由于焊缝是焊接管道缺陷产生的高发部位,对管道焊缝区域缺陷检测的研究具有很大的现实意义。
超声导波具有传播距离远、检测效率高等优点,被广泛运用于管道缺陷检测。由于导波的多模态和频散特性,可根据导波在裂纹等缺陷处发生模态转换及其反射波来判断是否存在缺陷。由于焊缝的弹性模量、密度等参数与管道存在差异,因此对于含缺陷的焊缝而言,既有焊缝反射回波,又有缺陷反射回波,且两者波包产生叠加,难以分离,使超声导波应用于焊缝缺陷检测变得困难。目前,使得用超声导波进行焊缝缺陷的检测大多集中在板焊缝的研究,例如Legendre等[1]用电磁超声导波提出小波分析信号处理方法,对板焊缝进行了检测。只有少数针对直管道单焊缝的研究成果。Nishino等[2]基于L(0,1)模态,对焊接管道进行了缺陷检测,总结了回波信号与缺陷大小的关系,但他并未对焊缝处的缺陷进行检测。刘秋阁[3]提出对称与非对称分离算法,实现了焊缝单缺陷的检测及周向定位,但未实现在前焊缝有缺陷的情况下对后焊缝进行缺陷的检测。Demma等[4]采用有限元分析了L(0,2)模态导波经过弯头时的模态转换情况,为本文弯管焊缝缺陷检测的研究奠定了基础。
在前人研究的基础上,本文运用对称与非对称模态分离算法,基于L(0,2)模态导波进行数值模拟,分别以前焊缝缺陷对称面、弯管对称面为纵坐标建立新的笛卡尔直角坐标系,得到横纵坐标方向上管道非对称幅值曲线,实现了双焊缝和弯管焊缝缺陷的识别和定量。
1 基本理论
1.1检测原理
超声导波在管道中的传播方式如图1所示。

图1 超声导波管道传播原理图Fig.1 Principle of ultrasonic guided wave propagation in pipes
超声导波在传播过程中,遇到不均匀材料介质会发生反射和频散。当遇到对称结构时,会产生对称的反射波;当遇到非对称结构时,会产生非对称的反射波。所以,导波遇到无缺陷焊缝,其反射回波是对称的,遇到含有缺陷的焊缝,其反射回波幅值将以缺陷为中心对称分布,缺陷处的反射回波幅值最大,以此来检测及定位焊缝缺陷。
1.2管道激励模态选择
根据弹性波动力学运动方程,管道的频散方程[5]见式(1):
|Cij|=0
(1)
其中,Cij为固体媒介的弹性系数(i,j为1,2,…,6),与管道尺寸、材料、波数有关。
焊缝坡口形状为V型,根据GB/T 31032—2014焊接标准,焊缝宽度为8 mm。超声导波频散现象表明焊缝宽度相对于管道长度影响较小,因此本文研究忽略了管道中焊缝对频散特性的影响。
本文研究对象为碳质量分数小于0.3%,外径100 mm,壁厚5 mm的碳钢管道。现用于检测管道缺陷的导波模态主要有纵波L(0,2)和扭转波T(0,1)模态。相对T(0,1)模态,L(0,2)具有传播速度快、易区分出缺陷波包、对管道周向、径向缺陷敏感、对轴向缺陷不敏感的特点[6]。结合焊缝缺陷一般表现为裂纹和腐蚀、以及轴向尺寸小的特点,本文选择L(0,2)模态导波对管道焊缝缺陷进行模拟。
2 焊缝缺陷数值模拟
2.1模型建立及网格划分
本文采用商业化软件ABAQUS对直管和弯管进行模拟。管道外径100 mm,壁厚5 mm。不考虑焊缝余高的影响。管道、焊缝材料参数如表1所示。
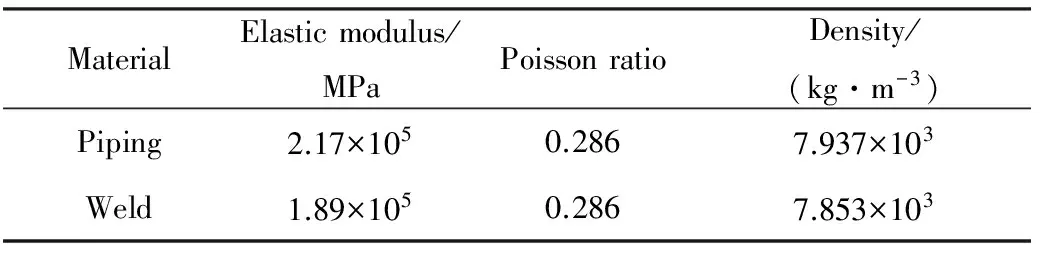
表1 管道与焊缝材料参数
结合对称与非对称分离算法,传感器数量大于该频率存在的非对称模态的最高阶数[7]。在管道端部周向均匀分布36个(4的倍数)节点来激励和接收。为对比不同截面缺损率对回波信号的影响,径向分5等份。根据波传动效应,一个波长方向至少20个单元[8],单元格周向长度a,有限元模拟时间步长h,总的计算时间H[9]应分别满足:
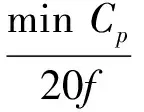
(2)
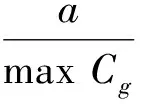
(3)
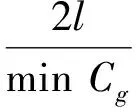
(4)
式中:Cp为导波相速度;Cg为导波群速度;f为激励频率;l为管道的总长度。
2.2双焊缝缺陷模拟
激励频率为70 kHz的L(0,2)模态导波分别对前后焊缝均无缺陷、前焊缝有缺陷后焊缝无缺陷、前焊缝有缺陷后焊缝有缺陷(前后焊缝缺陷对称面位于同一平面内)、前焊缝有缺陷后焊缝有缺陷(前后焊缝缺陷对称面位于不同平面内)的4种情况进行模拟分析。得到回波信号时程曲线如图2(a)~2(d)所示。
当双焊缝中均无缺陷时,从图2(a)时程曲线中依次可得到激励回波、两个焊缝回波及端面回波。当前焊缝存在缺陷时,如图2(b)所示,在两个焊缝回波间出现新模态波。但当前后焊缝均存在缺陷时,如图2(c)、2(d)所示,与图2(b)差异不大,很难辨别后焊缝是否存在缺陷。对比图2(a)~2(d)可以看出,利用L(0,2)模态导波可以有效识别前焊缝缺陷,但当前焊缝存在缺陷时,后焊缝的缺陷识别变得困难。
2.3弯管焊缝缺陷模拟
频率为70 kHz的L(0,2)模态导波分别对无焊缝、无缺陷焊缝、缺陷在弯管焊缝内壁、侧壁以及外壁的弯管进行了模拟,得到回波信号时程曲线如图3、图4所示。
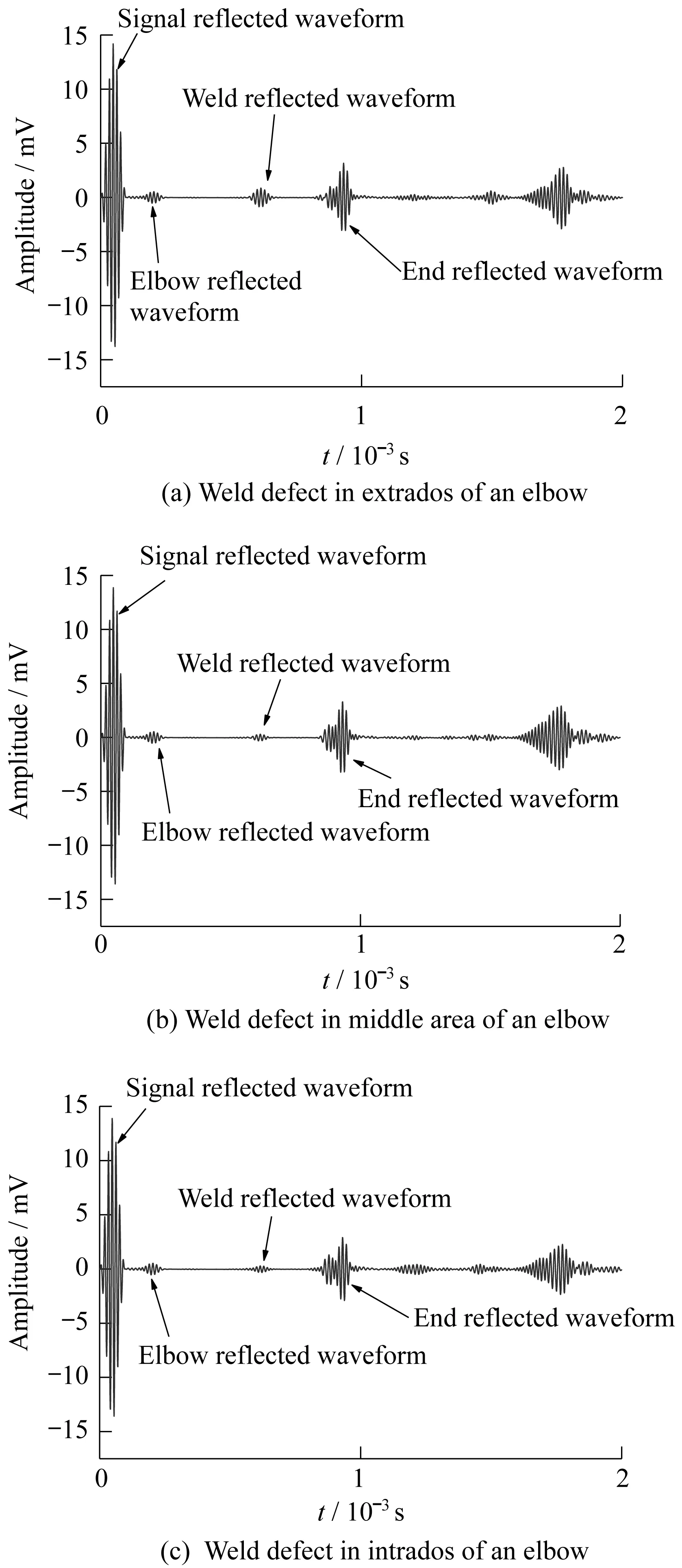
图3 弯管焊缝缺陷分布反射回波对比图Fig.3 Reflected waveform comparison of defect weld in different area of an elbow
对比图3(a)~3(c)可以发现,缺陷分布在弯头外壁的焊缝反射波幅值明显大于缺陷分布在弯头其他位置的反射波幅值。这一现象符合导波穿过弯头,能量由内侧向外侧转移,在弯头外侧聚焦的规律。
从图4(a)可以看出,弯管无焊缝模拟得到的时程曲线中,仅有由弯曲存在产生的新模态波包;图4(b)表明当弯管存在焊缝时,会出现焊缝波包。对比图4(b)和4(c)有缺陷和无缺陷的焊缝波形图,难以辨别焊缝处是否存在缺陷。
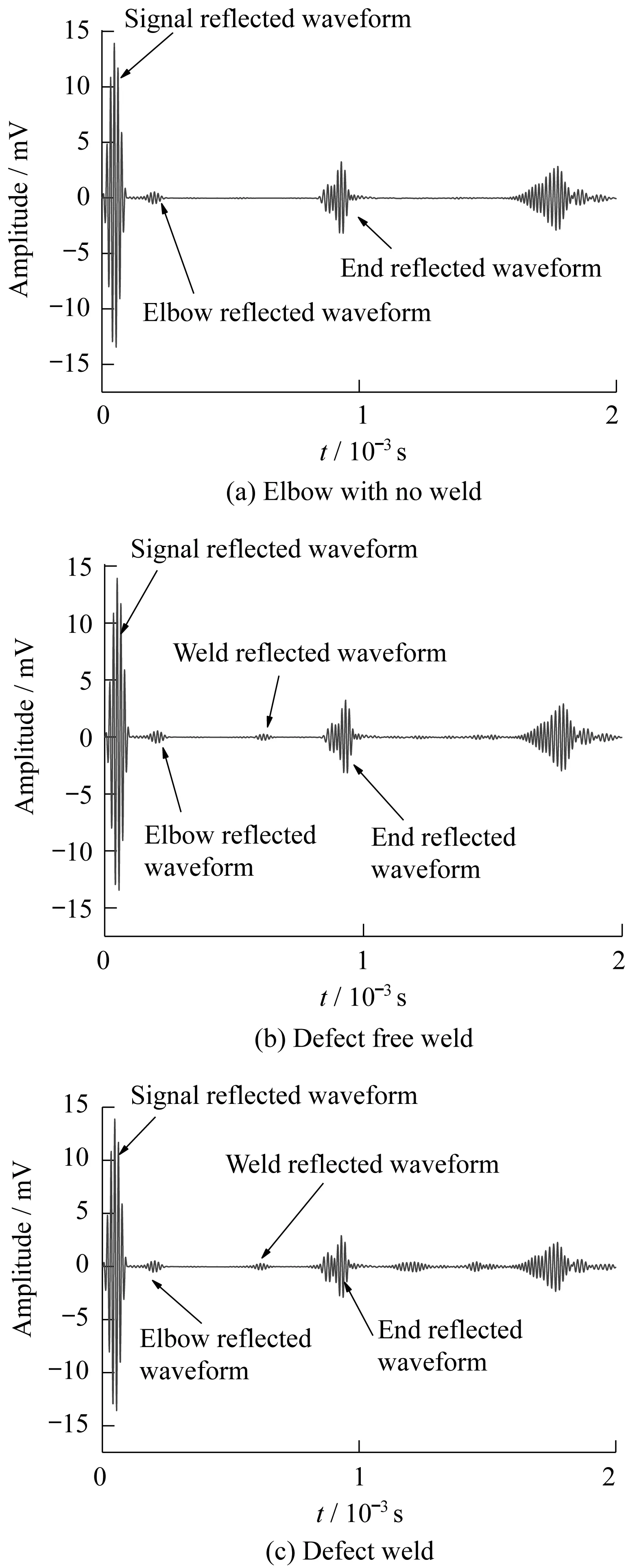
图4 弯管焊缝有无缺陷反射回波对比图
3 信号处理与结果分析
3.1对称与非对称模态分离
根据时程曲线图判断前焊缝反射回波波峰出现的时间,提取该时刻周向36个传感器反射波幅值,绘制成如图5所示雷达图。
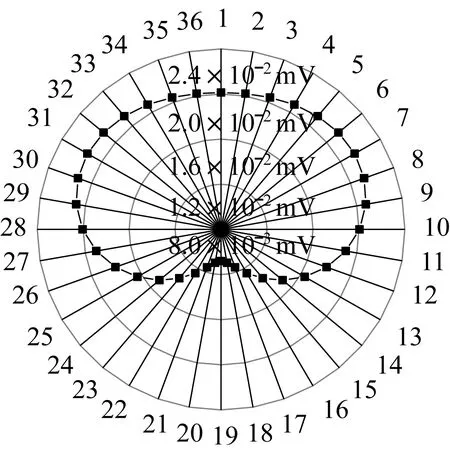
图5 前焊缝周向节点反射波幅值图Fig.5 Circumference amplitude value of the first weld
根据导波检测原理及图5中36个节点幅值分布可直接判断前焊缝缺陷关于1、19节点所在直线对称。基于文献[3]使用的模态分离方法,沿周向均匀布置36个传感器。分别以前焊缝缺陷对称面、弯管对称面为纵坐标建立新的笛卡尔坐标系,设计模态分离方法如下:
S=|S1+S2+…+S35+S36|
(5)
SH=|S2-S18|+|S3-S17|+…+|S9-S11|+
|S36-S20|+|S35-S21|+…+|S29-S27|
(6)
SV=|S2-S36|+|S3-S35|+…+|S18-S20|
(7)
其中:S为36个传感器接收到数值之和的绝对值;SH、SV分别为新的笛卡尔坐标系下以横坐标、纵坐标为对称轴,传感器数值之差的绝对值之和。SH、SV越大,表明非对称程度越大。
3.2双焊缝模态分离
在3.1节的理论基础上,进行双焊缝管道缺陷检测,得到前后焊缝均无缺陷、前焊缝有缺陷后焊缝无缺陷、前焊缝有缺陷后焊缝有缺陷(前后焊缝缺陷对称面位于同一平面内)、前焊缝有缺陷后焊缝有缺陷(前后焊缝缺陷对称面位于不同平面内)4种情况的模态分离图,如图6(a)~6(d)所示。
从图6(a)可以得到,当焊缝均不含缺陷时,SH、SV均为0。对比图6(b)、图6(c)可知,当前焊缝存在缺陷时,两个焊缝波包中,SH仍为0,SV不为0。与后焊缝无缺陷相比,后焊缝存在缺陷时焊缝波包波峰处SV增大。由图6(d)可得,当前后焊缝缺陷对称面位于不同平面时,后焊缝波包处SH、SV均不为0。
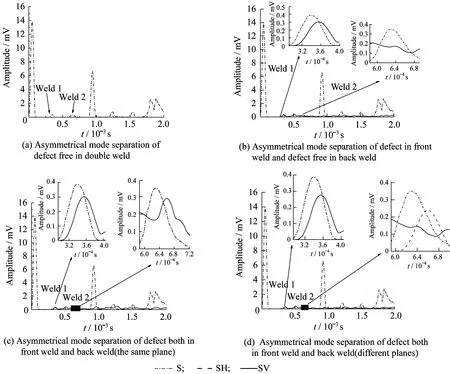
图6 双焊缝非对称模态分离图Fig.6 Asymmetrical mode separation of double weld
3.3弯管焊缝模态分离
以弯管对称面为纵坐标建立笛卡尔直角坐标系,对弯管无焊缝、弯管含无缺陷焊缝、弯管含内壁缺陷焊缝、弯管含侧壁缺陷焊缝以及弯管含外壁缺陷焊缝5种情况将弯管反射回波进行非对称模态分离,如图7所示。
从图7(a)、7(b)可以看出,弯管无焊缝和存在无缺陷焊缝时,在弯头和焊缝回波波包中,SH均为0,SV不为0。对比图7(c)~7(e)可得,当焊缝缺陷位于弯头内壁和外壁时,焊缝回波波包处SH仍为0,焊缝回波波包波峰处SV与图7(b)相比明显增大。当焊缝缺陷位于弯管侧壁时,如图7(d)所示,焊缝回波波包处SH和SV均不为0。
3.4焊缝缺陷定量
图8为焊缝内部缺陷截面示意图。图8中,R为管道外径,r为管道内径,α为缺陷沿圆周管道分布的弧度值,b为管道截面中心到缺陷壁面的距离,r≤b≤R。本文中,R=50 mm,r=45 mm。
因此,完整的圆环截面积A和内部缺陷的截面积Ain分别为
A=π(R2-r2)
(8)
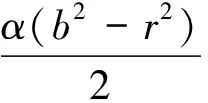
(9)
内部缺陷截面缺陷缺损率为
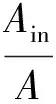
(10)
预制缺陷沿圆周管道分布的弧度α为π/9。分别取b为45、46、47、48、49 mm,根据公式(10)计算出相应的截面缺损率,提取焊缝回波波包与弯头回波波包波峰处的SH、SV,绘制弯管焊缝SH幅值随截面缺损率变化趋势图(图9)及焊缝回波波包与弯头回波波包波峰处SV之比随截面缺损率变化趋势图(图10)。
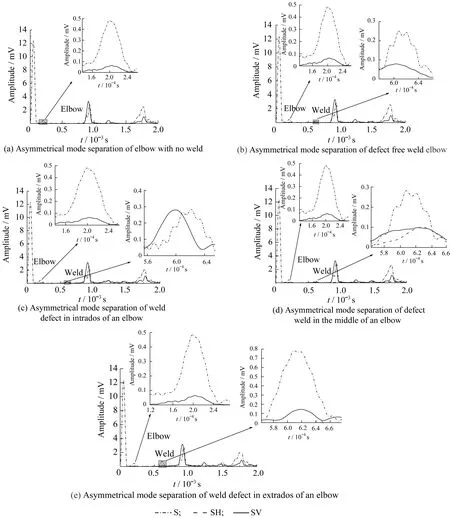
图7 弯管焊缝非对称模态分离图Fig.7 Asymmetrical mode separation of weld elbow
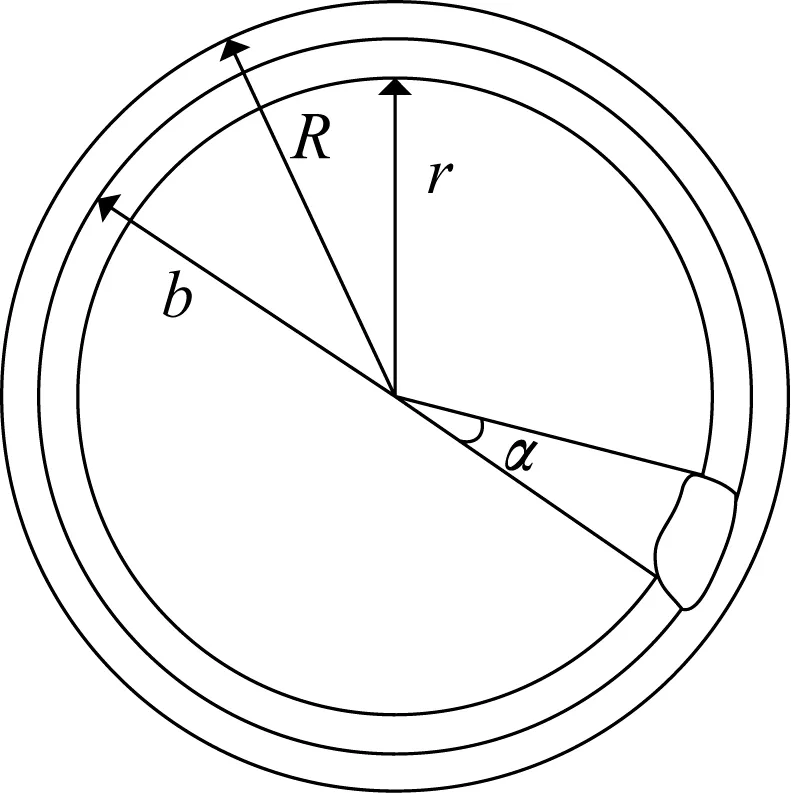
图8 焊缝缺陷示意图Fig.8 Schematic diagram of weld defect

图9 弯管焊缝SH幅值随截面缺损率变化趋势图Fig.9 Variation trend of SH amplitude with section defect rate in bend weld
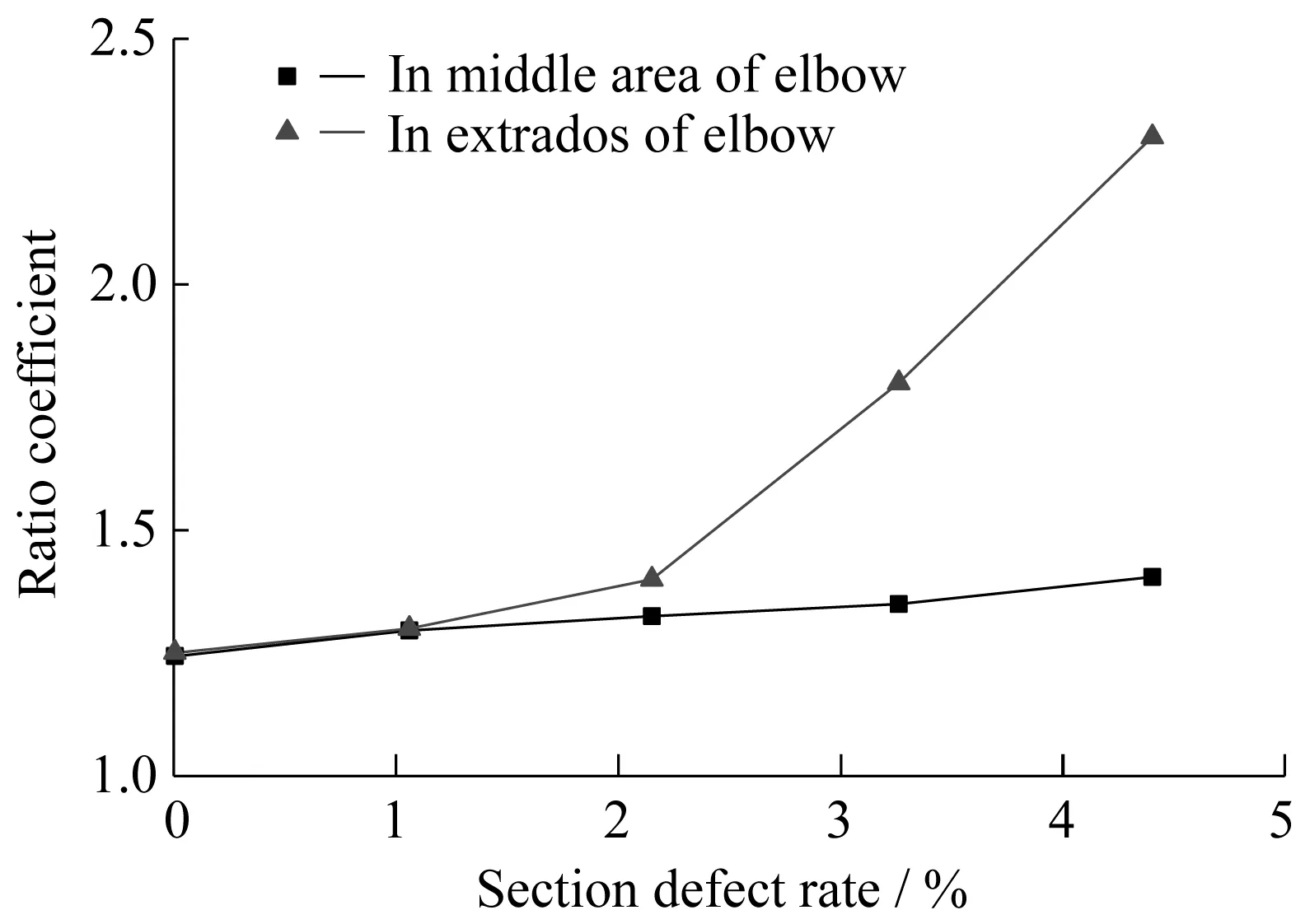
图10 弯管焊缝SV之比随截面缺损率变化趋势图Fig.10 Variation trend of ratio coefficient with section defect rate in bend weld
图9表明,当焊缝缺陷对称面与弯管对称面在同一平面时,SH为0。当焊缝缺陷对称面与弯管对称面不在同一平面时,SH大于0,且随截面缺损率增大而增大。图10表明,当焊缝回波波包与弯头回波波包波峰处SV之比大于1.24即可大致判断弯管焊缝存在缺陷。以弯管外壁缺陷为例,得到焊缝回波波包与弯头回波波包波峰处SV之比关于截面缺损率的拟合函数,实现缺陷定量,见式(11):
y=0.136 05ex/2.016 46+1.073 64
(11)
4 结 论
本文在模态对称分离算法检测单焊缝管道缺陷的基础上,分别以前焊缝缺陷对称面、弯管对称面为纵坐标建立新的笛卡尔坐标系,利用ABAQUS软件,基于L(0,2)模态导波进行数值模拟,给出了双焊缝缺陷及弯管焊缝缺陷识别的定量方法。主要得出了以下结论:
(1) 模拟空管双焊缝缺陷识别时,当时程曲线图出现新模态波包时可判断前焊缝存在缺陷。根据前焊缝周向节点反射波幅值分布雷达图,可确定前焊缝缺陷对称面。
(2) 模拟管道双焊缝缺陷和弯管焊缝缺陷识别时,仅根据时程曲线图难以判断焊缝处是否存在缺陷。进行模态非对称分离后,当后焊缝、弯管焊缝回波波包处SH大于0时即可判定焊缝处存在缺陷;当SH为0时,需根据焊缝回波波包与弯头回波(前焊缝回波)波包波峰处SV之比判断。当焊缝回波波包与弯头回波波包波峰处SV之比大于1.24时,可确定弯管焊缝处存在缺陷。
[1] LEGENDRE S,MASSICOTTE D,GOYETTE J.Neural classification of Lamb wave ultrasonic weld testing signals using wavelet coefficients [J].Instrumentation and Measurement,2001,50(3):672-678.
[2] NISHINO H,MASUDA S,MIZOBUCHI Y,etal.Long-range testing of weld elbow pipe using theT(0,1) mode ultrasonic guided wave [J].Japanese Journal of Applied Physics,2010 ,49(11):1166021-1166026.
[3] 刘秋阁.基于超声导波的管道焊缝区缺陷检测研究[D].江苏:江苏大学,2016.
[4] DEMMA A,CAWLEY P,LOWE M,etal.The effect of bends on the propagation of guided waves in pipes [J].Journal of Pressure Vessel Technology,2005,127:328-335.
[5] 谭冰心,戴波.管道腐蚀缺陷超声导波检测数值模拟 [J].控制工程,2015,22(2):335-341.
[6] ALLEYNE D N,LOWE M J S,CAWLEY P.The reflection of guided waves from circumferential notches in pipes [J].Journal of Applied Mechanics,1998,65(9):635-641.
[7] 程载斌,王志华,张立军,等.管道超声纵向导波裂纹检测数值模拟[J].应用力学学报,2004,21(4):76-79.
[8] SAEED Moaveni.有限元分析:ANSYS理论与应用[M].北京:电子工业出版社,2009:493-499.
[9] FRIEDRICH M,LAURENCE J,QU Jianmin.Modeling elastic wave propagation in waveguides with the finite element method[J].NDT and E International,1998,32:225-234.
SimulationforWeldDefectsinPipeBasedonModalSeparationAlgorithm
YEMeng-ya,HUMing-hui
(KeyLaboratoryofPressurizedSystemandSafety,MinistryofEducation,EastChinaUniversityofScienceandTechnology,Shanghai200237,China)
With the influence of temperature,pressure,medium corrosion and vibration,small defects in the weld can be grown into cracks,which will do harm to the in-service industrial pipelines.Based on the modal symmetry algorithm of defect detection of single weld pipeline,the simulation of modal guided waves inL(0,2) is carried out.According to the symmetry principle,it’s easy to extract the defect features.A new Cartesian coordinate is established by using the symmetry surface of the weld defects and weld elbow as the vertical axis respectively.The simulation results show that the asymmetric amplitude is in exponential function with the crack depth,and the method can realize the identification and quantification of defects in double welds and elbows.
ultrasonic guided wave; weld defect; mode separation; longitudinal modeL(0,2); simulation
TB559
A
1006-3080(2017)05-0717-07
10.14135/j.cnki.1006-3080.2017.05.018
2017-04-24
国家自然科学基金(51205133)
叶梦雅(1991-),女,浙江丽水人,硕士生,研究方向为管道焊缝缺陷导波检测。E-mail:ymyeah122@163.com
胡明慧,E-mail:agile_hu@ecust.edu.cn

