柴油机可变相位参数耦合对气路状态的影响

吴学舜， 杜德峰， 李均同， 韩志强

(西华大学 汽车与交通学院， 四川 成都 610039)

发动机进气门型线对发动机气路状态参数有决定性的影响，在有效组织缸内混合气温度、压力和组分的情况下，影响燃烧过程，从而决定发动机的性能[1].

针对进气门型线对进气状态参数的研究，国内外学者进行了大量研究.H. U. BASARAN等[2]在六缸柴油机上进行了试验，研究了低负荷下，进气门早关或晚关对排气温度的影响，发现进气门早关65°(文中角度为曲轴转角)或者晚关100°都可以将柴油机后处理装置入口温度增加到250 ℃以上，这样能够提高后处理的效率.Y. MURATA等[3]通过仿真发现，随着附加升程产生的延迟，气门关闭角相比原机进气相位滞后，有效压缩比逐渐降低，当进气门延迟关闭60°，有效压缩比下降3.3.J. JUNG等[4]、A. F. M. MAHROUS 等[5]、I. CAMERON等[6]通过数值模拟也得到相似结论.张翔宇等[7]利用ANESIM软件建立电液可变气门机构模型，研究了进回油管直径对气门升程特性的影响，结果表明，进回油管直径对气门落座速度有重大影响，在优化气门落座速度时存在最优值.潘锁柱等[8]、尹胧等[9]建立了柴油机可变气门系统的数值模型，分析了附加升程限位对进气状态参数的影响，研究表明，最大附加升程限位对进气质量流量影响很小，最大附加升程限位对压缩终了温度和压力影响也很小.

然而，以上文献并未就柴油机气门型线关键参数的耦合作用对进气状态参数的影响关系进行深入研究.为此，笔者以DK4A柴油机气门型线为研究对象，通过系统化分析单位附加升程持续角和单位附加升程峰值与原机气门型线峰值间隔角的耦合作用对进气状态参数的影响规律，探讨两者对进气状态参数的影响权重变化规律.

1 模型的建立和验证

1.1 模型的建立

为分析柴油机可变相位参数耦合对气路状态参数的影响规律，建立了热力学模型.仿真模型的热力学方程遵守质量守恒原理、能量守恒原理.具体模型假设与方程详见文献[10].

1.2 输入参数

以DK4A柴油机为对象，建立热力学模型，柴油机主要输入参数如下：发动机进气排量为2 498 mL,行程为94 mm，缸径为92 mm，压缩比为18.5 ∶1，每缸气门数为4个，进气门开启提前角为30°,进气门关闭迟闭角为40°.模型输入进气门型线由原机升程曲线与附加升程曲线叠加而成，排气上止点时刻定义为0°，具体曲线如图1所示，θ1为原机气门开启角，θ2为原机气门关闭角.附加升程曲线对称分布，具体由3个参数确定，即单位附加升程峰值与原机气门型线峰值间隔角β、附加升程高度h和单位附加升程持续角α.

图1 附加升程气门型线与原机气门型线

从图1可以看出：进气门气门型线的气门相位受附加升程参数中β和α的影响，进气门的升程高度受附加升程h影响.

1.3 模型的验证

为确保模型准确，具有可预测性，课题组采用原机气门型线对DK4A柴油机十三工况点(怠速，A25，A50, A75，A100,B25，B50, B75，B100, C25，C50, C75，C100)进行模型验证，进气质量流量q仿真与试验数据对比如图2所示.

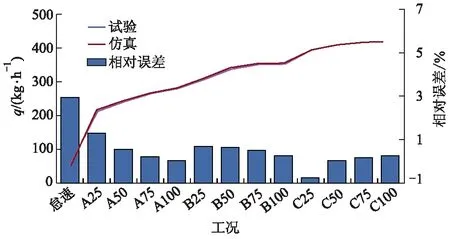
图2 进气质量流量仿真与试验数据对比

从图2可以看出：仅怠速时进气质量流量仿真与试验的相对误差达到了2.7%，其余各工况的质量流量仿真与试验的相对误差均在2.0%以内.

转矩仿真与试验数据对比如图3所示.

图3 转矩仿真与试验数据对比

从图3可以看出，各工况转矩仿真与试验的相对误差控制在2.0% 以内.因此认为所建模型准确，可用于预测柴油机进气门附加升程曲线对缸内进气状态参数的影响规律.

2 评价指标

为有效评价β和α的耦合作用对进气状态参数(进气质量流量q，气缸压缩上止点温度Tc，气缸压缩上止点压力pc)的影响权重，建立如下评价体系：

变化量为

Δχn=χn1-χn2，

(1)

式中：Δχn分别为q，Tc和pc的变化量；n分别为β和α；χn1，χn2分别为不同状态下的q，Tc和pc.

变化率为

γn=Δχn1-n2/(n1-n2),

(2)

式中：γn分别为q，Tc和pc的变化率；n1-n2为变化区间的长度.

3 结果分析

发动机运行在转速为2 800 r·min-1，负荷为50%，h为3.5 mm的条件下，分析β与α的耦合作用对进气状态参数的影响规律.

3.1 β与α的耦合作用对q的影响

β与α的耦合作用对q的影响如图4所示，随着β，α的增大，q均呈现减小的趋势.当β=140°，α=132°时，q达到最小值，仅有182 kg·h-1.

为了分析β与α的耦合作用对q的影响权重，研究了单位附加升程峰值与原机气门型线峰值间隔角变化量Δβ与单位附加升程持续角变化量Δα对进气流量变化量Δq的影响规律.Δq与双参数(α，Δβ)的耦合关系如图5所示.

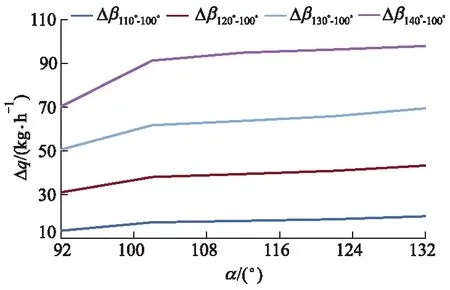
图5 Δq与双参数(α，Δβ)的耦合关系

从图5可以看出：α为92°～132°时，Δq随着Δβ的增加而增大，α越大Δq越大，这是因为在α为定值时，随着Δβ的增加，气门关闭角越远离进气下止点，更多的进气倒流回进气管，所以Δq越大；当Δβ为定值，α为92°～132°时，随着α的增加，Δq增加的速率由快变慢，这是因为，由图1可知，当β≤(θ2-θ1-α)/2=80°时，进气门关闭角与原机关闭角一致，当β>(θ2-θ1-α)/2=80°时，进气门关闭角较θ2延迟；α从 92°变化到132°过程中，β均处于大于临界值80°的状态，进气门关闭角较θ2延迟，气门关闭角处于压缩下至点后，这意味着在压缩冲程，α越大，相同相位时气门流通截面逐渐增加，产生进气回流突增，因此Δq变化率大；随着流通截面增加，流量系数变化梯度逐渐变小，所以Δq变化率减小；α=132°的Δq比α=92°的Δq增加了1.40～1.50倍.因此Δβ的增加可以放大α对Δq的影响.

Δq与双参数(Δα，β)的耦合关系如图6所示.

图6 Δq与双参数(Δα，β)的耦合关系

从图6可以看出：β为 100°～140°时，Δq随着Δα的增加而增加，且β越大，Δq越大，这是由于Δα增加，气门流通截面变化持续期增加，回流量增加，因此Δq越大；当Δα为定值时，随着β增加，进气关闭角离进气下止点逐渐变远，回流的进气逐渐大于流通截面增加而多流入缸内的气体，Δq斜率越大；β为 140°的Δq比β=100°的Δq增加了1.90～2.67倍.由此可知，Δα能放大对β的影响.

α与β对γq的影响权重等量关系分别如图7，8所示.

图7 α对γq的影响权重等量关系

图8 β对 γq的影响权重等量关系

从图7，8可以看出：α=92°～132°，β=100°～130°时，随着α和β的增加，γq逐渐增大，图8中出现γq值相等的交点，即为α和β的耦合作用对γq的影响权重相等的情况，将类似的交点进行统计分析后得到图9.

图9 α和β的耦合作用对γq的影响

从图9可以看出：当α保持不变时，随着β的增加，γq增加，表明α不变时，β增加有利于增加其对进气量的影响权重；当β保持不变时，随着α的增加，γq先减小后增加，即β保持不变，随着α的增加，α对进气量的影响权重先减小后增加，影响权重最小值出现在α=124°～125°范围内，这是因为，附加升程会导致气门型线产生第2个峰值，如图1所示；当β保持不变，随着α的增加，第2个峰值将向原机气门型线峰值靠近，这意味着相比原机，相同进气相位的气门时面值增大，但关闭角延迟，综合2方面因素，当α=124°～125°时，γq最小.

Δβ与Δα对γq的影响如图10所示，当Δβ保持不变时，随着Δα的增加，γq缓慢增加；当Δα保持不变，随着Δβ增加，γq增速更大，这意味着，Δβ比Δα对γq的影响权重更大.

图10 Δβ与Δα对γq的影响

3.2 β与α耦合对压缩上止点温度Tc的影响

β与α耦合作用对Tc的影响如图11所示，随着β，α的增大，Tc均呈现减小的趋势.当β=140°，α=132°时，Tc达到最小值，仅有1 059 K.

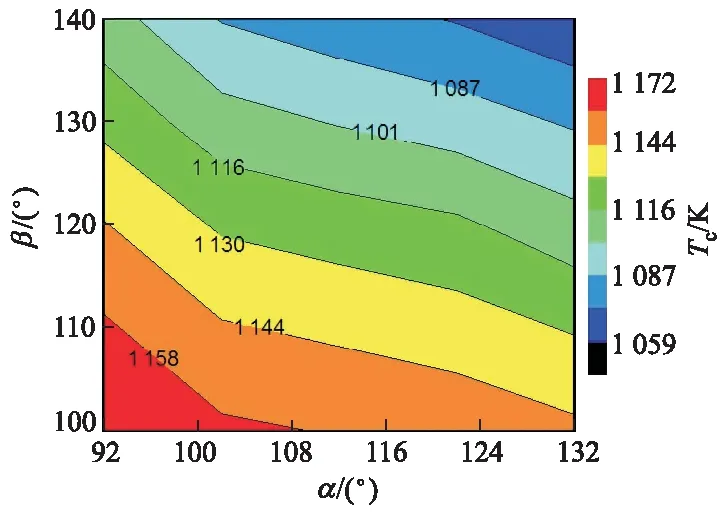
图11 β与α耦合作用对Tc的影响

ΔTc与双参数(α，Δβ)的耦合关系如图12所示，α为92°～132°时，ΔTc随着Δβ增加而增加，且α越大，ΔTc越大.这是因为在α为定值时，随Δβ增加气门关闭角越远离进气下止点，有效压缩比降低，缸内气体在压缩上止点被压缩的程度减弱，所以ΔTc增加.当Δβ为定值时，α为92°～132°，随着α的增加，ΔTc增加的速率由快变慢.这是因为Δβ直接影响气门流通截面的变化，在α较小时，进气流量系数变化梯度很大，回流到进气管的气体突增，所以ΔTc增加速率快.α较大时流量系数变化梯度逐渐变小，ΔTc增加速率变慢.此外，α=132°时的ΔTc比α=92°时的ΔTc增加了1.32～1.58倍.因此，Δβ可以放大α对ΔTc的影响.

图12 ΔTc与双参数(α，Δβ)的耦合关系

ΔTc与双参数(Δα，β)的耦合关系如图13所示，β为100°～140°时，随着Δα的增加而增加，且β越大，ΔTc越大；同时，当Δα为定值时，随着β的增加，进气关闭角离进气下止点逐渐变远，发动机在压缩冲程中回流的进气量增加，这导致了发动机有效压缩比逐渐变小，ΔTc斜率越大；β=140°时的ΔTc比β=100°的增加了1.80～1.90倍.由此可知，Δα能放大β对ΔTc的影响.

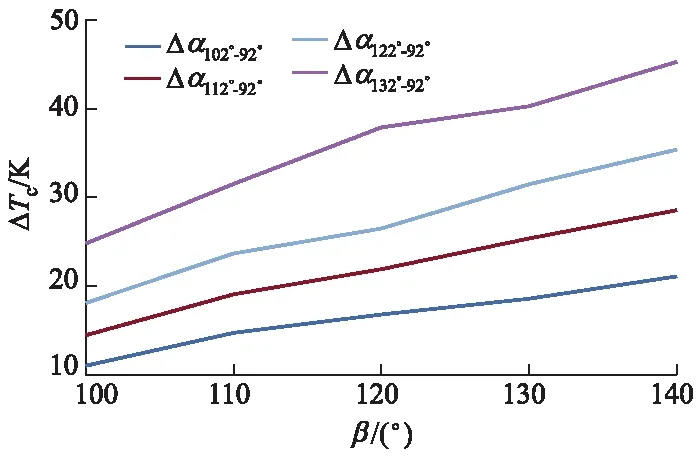
图13 ΔTc与双参数(Δα，β)的耦合关系

α与β对压缩上止点温度变化率γTc的影响权重等量关系分别如图14，15所示，在α=100°～132°，β=100°～132°时，随着α和β的增加，γTc逐渐增大，图15中出现γTc值相等的交点，即为α和β的耦合作用对γTc的影响权重相等的情况.将类似的交点进行统计分析后得到图16.

从图16可以看出：当α保持不变时，随着β的增加，γTc增加，即表明α不变时，β增加有利于增加其对压缩上止点温度的影响权重；而当β保持不变时，随着α的增加，γTc值先减小后增加，即β保持不变，随着α的增加，α对压缩上止点温度的影响权重先减小后增加，影响权重最小值出现在α=123°～124°范围内.这是因为，附加升程会导致气门型线产生第2个峰值，如图1所示.当β保持不变时，随着α的增加，第2个峰值将向原机气门型线峰值靠近，有效压缩比降幅减小，所以在α=124°～125°时，压缩上止点温度变化率最小.

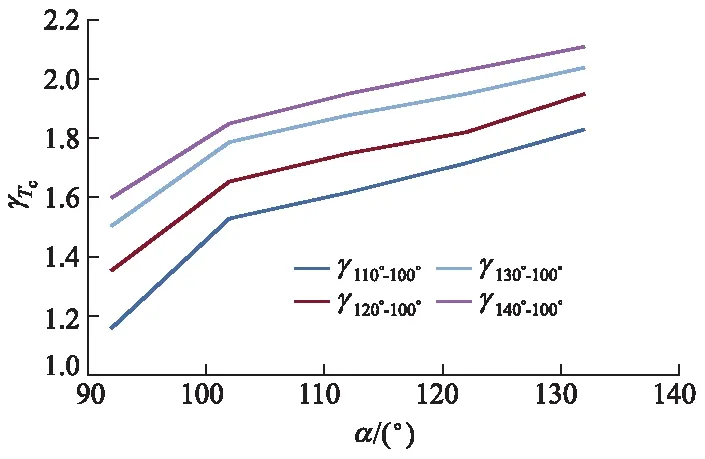
图14 α对γTc的影响权重等量关系

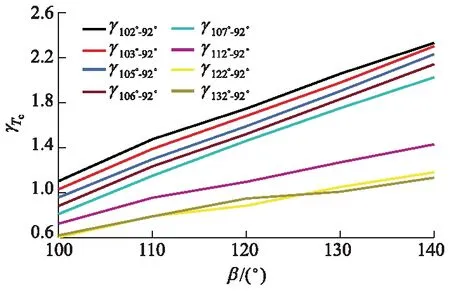
图15 β对γTc的影响权重等量关系

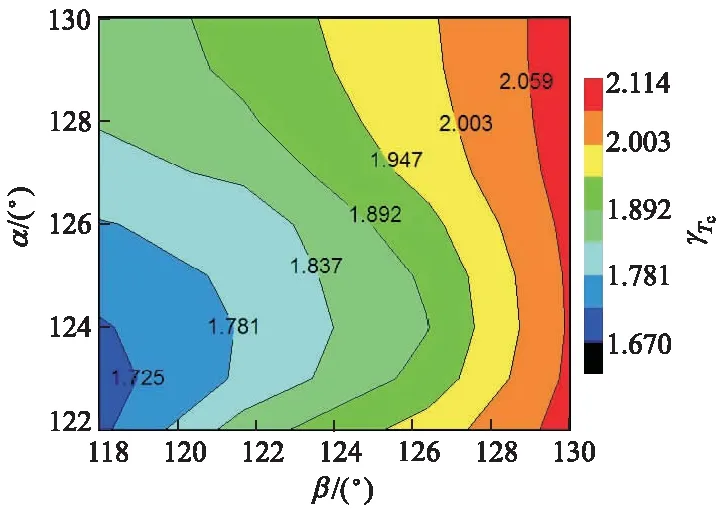
图16 α与β的耦合作用对γTc的影响

Δβ与Δα对γTc的影响如图17所示.

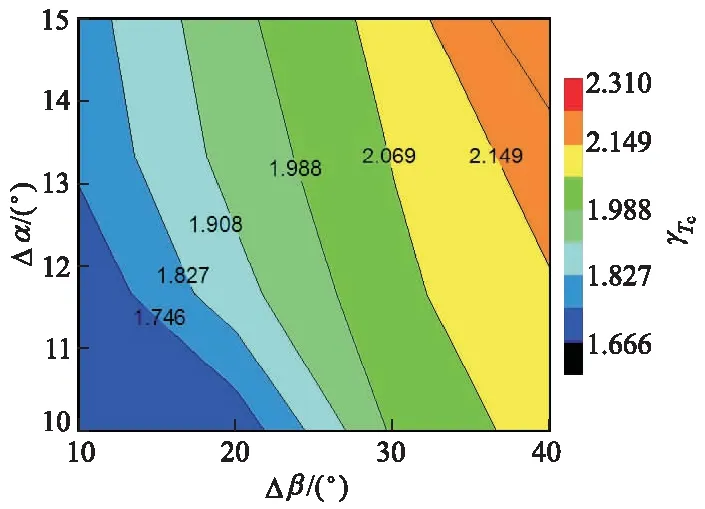
图17 Δβ与Δα对γTc的影响

从图17可以看出： 当Δβ保持不变时，随着Δα增加，γTc缓慢增加；当Δα保持不变时，随着Δβ增加，γTc增速更大，这意味着，有效压缩比的变化，Δβ比Δα对γTc的影响权重更大.

3.3 β与α耦合对压缩上止点压力pc的影响

β与α的耦合作用对pc的影响如图18所示，随着β，α的增大，pc均呈现减小的趋势.当β=140°，α=132°时，pc达到最小值，仅有4.990 MPa.

图18 β与α的耦合作用对pc的影响

Δpc与双参数(α，Δβ)的耦合关系如图19所示，当α=92°～132°时，Δpc随着Δβ的增大而增大，Δβ越大，Δpc越大.这是因为在α为定值时，随Δβ的增大，气门关闭角越远离进气下止点，发动机压缩冲程中回流的充量就越多，活塞到达压缩上止点时的有效压缩比越小，所以Δpc越大.当Δβ为定值时，α=92°～132°，随着α的增加，Δpc增加的速率由快逐渐变慢.此外，α=132°时的Δpc比α=92°的Δpc增加了1.30～1.44倍.

图19 Δpc与双参数(α，Δβ)的耦合关系

Δpc与双参数(Δα，β)的耦合关系如图20所示，当β=100°～140°时，Δpc随着Δα的增加而增加，且β越大，Δpc越大.这是由于Δα增加，相比原机进气相位的气门流通截面积增加，因此Δpc越大；当Δα为定值时，随着β的增加，进气门的关闭角逐步延迟到压缩下止点后，随着活塞上行，气门处于开启状态，被推出的气体增多，发动机有效压缩比降低，压缩上止点压力减小，Δpc斜率增加.Δα能放大β对Δpc的影响.并且，在α=132°时的Δpc比α=92°的增加了1.95～2.07倍.

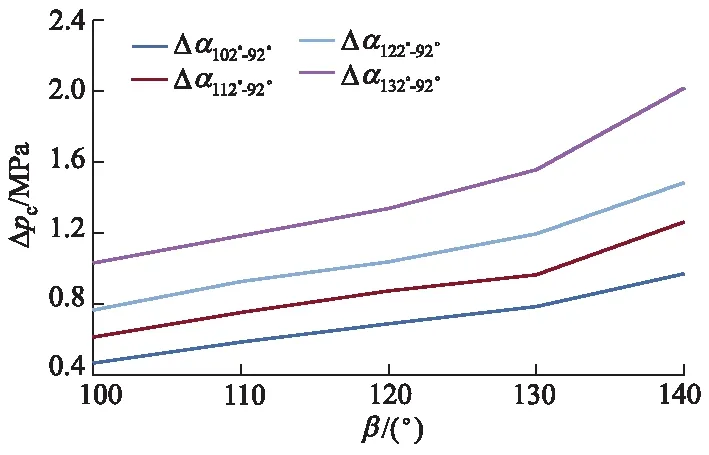
图20 Δpc与双参数(Δα，β)的耦合关系

α与β对压缩上止点压力变化率γpc的影响权重等量关系分别如图21，22所示，当α=132°，β=132°时，随着α和β的增加，γpc逐渐增大，图22中出现γpc值相等的交点，即为α和β的耦合作用对γpc的影响权重相等的情况.将类似的交点进行统计分析后得到图23，24，当α保持不变时，随着β增加，γpc增加，即α不变时，β增加有利于增加其对压缩上止点压力的影响权重；而当β保持不变时，随着α的增加，γpc值先减小后增加.即β保持不变时，随着α的增加，α对压缩上止点压力的影响权重先减小后增加，影响权重最小值出现在α=124°～125°范围内，这是由于在此区间有效压缩比降幅减小.

图21 α对γpc的影响权重等量关系

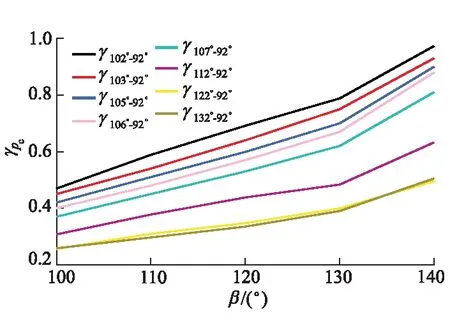
图22 β对γpc的影响权重等量关系

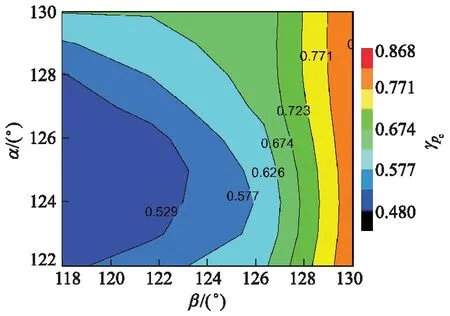
图23 α与β的耦合作用对γpc的影响

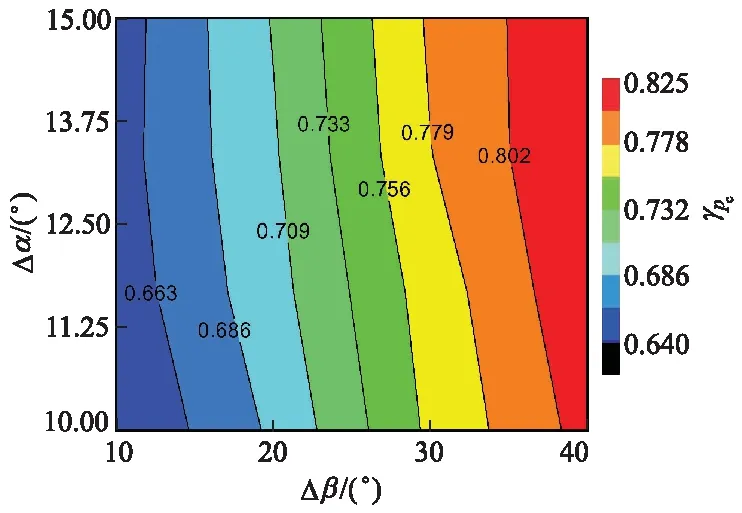
图24 Δβ与Δα对γpc的影响

4 结 论

β与α的耦合作用对进气状态参数变化率的影响存在权重相等的情况，且Δβ对Δα的影响权重大；当α保持不变时，β的增加有利于增加其对进气状态参数的影响权重；当β保持不变时，α存在临界区间，使得其对进气状态参数变化率的影响最小；Δα的增加能放大β对进气状态参数变化量的影响；Δβ的增加能放大α对进气状态参数变化量的影响；随着β和α的增大，进气状态参数值呈现出减小的趋势.当α保持不变时，Δβ对进气状态参数的影响会存在一个临界值使得进气状态参数的变化量突增.