混合分数布朗运动下分离交易可转债的定价*
陈飞跃,陈 煜,杨 蓉,龚海文
(1.保险职业学院 金融系,湖南 长沙 410114;2.长沙理工大学 数学与计算科学学院,湖南 长沙 410114)
1 引 言
分离交易可转债(Separable and Convertible Bonds)是上市公司公开发行的 “认股权”和“债券”分离交易的可转换公司债券[1].分离交易可转债赋予持有人在债券到期前规定的时间内按照约定的执行价格和行权比例购买上市公司股票的权利.当然,到期前若股票市价低于行权价格,则投资者将放弃认股权.当分离交易可转债的持有人行使了期权后,依旧持有债券,仍可定期获取利息,到期收回本金,故分离交易可转债具有一次发行两次融资的优点.投资者最初购买分离交易可转债,对发行人来说属于“债权融资”,若投资者后来行使了期权,缴纳认股款则属于“股权融资”.而普通可转债的持有人在债券到期前一旦执行转换,则其债权就不复存在了.因此,人们通常认为分离交易可转债是一种“买债券送权证”的新型衍生金融工具.
20世纪70年代美国证券市场通过金融创新,率先提出了分离交易可转债概念,经过40多年的发展,目前分离交易可转债已成为美国证券市场比较成熟的一种新型衍生证券.Ingersoll[2,3]最早将Black-Sholes 期权定价公式用于可转债定价,通过分析投资者的最优转换策略以及发行人的最优赎回策略,得到了可转债定价的显示表达式.Finnerty[4]通过对机构投资者进行调查发现,分离交易可转附带权证带来的折价发行会增加投资者的税收负担,从而会使投资者望而却步.近年来,国内一些学者也积极探讨了可转债的定价问题.李争华[5]以宝钢分离交易可转债为例,利用稀释效应的期权定价模型详细研究了其定价问题,得出结论:宝钢分离交易可转债的“债券”定价比较合理,但“权证”定价稍许偏高于其实际价格.骆桦、沈红梅[6]基于国内可转债市场的实际情况,应用Black-Shocles模型推导出分离交易可转债定价的表达式,并分析了分离交易可转债带来的股权稀释效应.我国学者江良、林鸿熙等[7]探讨了基于随机利率模型下可转换债券的定价问题,研究表明:常数利率和随机利率对可转换债券价格的影响不存在显著的差异.
以上可转债定价问题研究均以股票市价服从标准布朗运动为假设前提.Peter[8]首先提出分形市场假说,通过分析股票价格和外汇汇率等金融资产的波动,发现金融市场存在分形结构和非周期循环的特点.同时,行为金融学的大量实证研究也表明:股票、外汇、基金等金融资产的价格过程具有自相似性、长期依赖性、长记忆性等特征,并不是随机波动的,金融资产的对数收益率并不服从正态分布,而是呈现出“尖峰厚尾”的特点.由于分数布朗运动是一种高斯过程,具有自相似性、厚尾性、长期相关性以及加法不变性等性质,这些性质使得分数布朗运动能较好地拟合股票、外汇、基金等金融资产的变化过程.Duncan等[9]、Hu和Øksendal[10]、Elliott和Van等[11]在这方面做了一些开创性贡献,他们利用Malliavin随机分析理论和Wick积的概念,把分数布朗运动的积分定义为FWIS随机积分(Fractional Wick ItSkorohold integral,FWIS integral),并证明了基于FWIS积分框架和Wick自融资策略的分数B-S金融市场模型中无强套利机会,并且金融市场是完备的,随后,Necula[12]在FWIS积分框架下,分别利用拟条件期望和delta对冲法推导出分数B-S公式.陈飞跃[1]构建了股票价格遵循分数布朗运动下分离交易可转债的定价模型,并推导出了其风险中性定价公式.
然而,Hurst参数H>1/2的分数布朗运动既不是马尔科夫过程,也不是半鞅,不能用通常定义的随机积分进行分析,从而分数布朗运动在金融上的应用并非易事.Björk和Hurt[13]的研究表明Wick资产组合导致无套利,但定义自融资交易策略受到严格的限制.因此,尽管基于Wick积分的分形市场被认为一个完美的数学结构,但其在金融中的适用性受到限制.当Hurst参数H>1/2时,混合分数布朗运动是一个特殊的长记忆过程.为了克服用分数布朗运动描述金融资产价格变化时存在的缺陷,同时考虑金融资产价格过程所具有的长记忆性特征,使用混合分数布朗运动能更好地来刻画金融资产的价格变化过程.Sun[14]关于混合分数布朗运动下的欧式汇率期权定价研究结果支持了以上结论.
目前,国内外还很少有文献研究混合分数布朗运动下分离交易可转债的定价问题.本文假定股票价格变动由混合分数布朗运动驱动和市场利率服从Vasicek过程的条件下,建立了分离交易可转债定价的金融市场偏微分方程.通过求解偏微分方程、并利用无套利定价原理得到了分离交易可转债定价的显示解,从而为研究分形市场中金融衍生品估值方法提供参考.用混合分数布朗运动驱动的随机偏微分方程刻画股价变化,其中表征收益率长程自相关性的Hurst参数H满足1/2 分离交易可转债通常包括:标的股票、票面利率、行权价格、附权证比例、行权比例、行权期限等要素. 1)标的股票:即分离交易可转债发行公司发行的股票,如“江西铜业可转债”的标的股票就是江西铜业股票. 2)票面利率:就是分离交易可转债发行时规定的债券部分的利率,由于分离交易可转债包含了认股权证,故其票面利率通常低于普通债券利率和银行利率. 3)执行价格:即行权价格,是投资者在行使认购权时购买标的股票的协议价格. 4)附权证比例:是指发行人给投资者购买的每份分离交易可转债免费派送的股票权证的数量. 5)行权比例:是指每份股票权证可以认购发行公司股票的数量. 6)行权期限:通常是指分离交易可转债发行之后,发行人规定的从某时点开始至债券到期日之间持有人可以行使认股权的这段时间. 分离交易可转债的价值等于“债券”价值与“股票看涨期权”价值之和,其到期时的价值为 其中,M表示分离交易可转债的票面价值,Pb=MeiT表示按票面利率i连续复利计息得到的债券到期时的价值,Cv表示执行价格,T表示到期时间,ST表示T时刻的标的股票的价格,α表示附权证比例,β表示行权比例. 1)定义 设(Ω,F,P)是一完备概率空间,混合分数布朗运动是由相互独立的标准布朗运动和分数布朗运动组成的一个线性组合,由下式给出(t∈R+): 证明见参考文献[15]. 1)金融市场无摩擦,即税收和交易费可以忽略不计; 2)所有证券可以无限制的细分,证券交易是连续进行的,且交易头寸和交易方向都不受限制,无最大持有定额限制; 3)所有投资者可以及时免费获得充分的市场信息,市场不存在无风险套利机会; 4)暂不考虑分离交易可转债的违约风险. 1)由于可转债不是短期衍生证券,从而不将市场利率设为常数,假定市场利率服从Vasicek过程,即 dr(t)=k(θ-r(t))dt+δdB2(t). (1) 其中k为均值回复率,θ为利率均值,k,θ,δ均为正常数,B2(t)是一标准布朗运动; 2)假定标的股票的价格{S(t)或St,t≥0}满足如下随机微分方程(SDE): (2) (3) 根据Nualart和Taqqu[16]中的Wick It公式: 从而对∀T>t>0,有 (4) 证明由方程(1)可得:dr(t)+k·r(t)dt=kθdt+δ·dB2(t),等式两边同时乘以ek·t,则有 ek·tdr(t)+k·r(t)·ek·tdt=ek·tkθdt+ek·tδ·dB2(t). 对t≤u≤T,上述等式两边在[t,u]积分,得到 将上式右边最后一个二重积分交换积分次序可得 (5) 由文献[17]可知 即,Z(t,T)~N(0,σ2(t,T)). 4.1 引理2设Z1~N(0,1),Z2~N(0,1),Cov(Z1,Z2)=ρ,则对任意实数a,b,c,d,s,有下式成立: 4.2 定理假定股票价格变动由混合分数布朗运动驱动,且市场利率遵循Vasicek过程,则分离交易可转债在到期前任意时刻t的理论价值为 (6) 证明由无套利定价原理(风险中性定价原理)可知, 记上式中的第一项为V1,第二项为V2,先计算第一项V1, 注意到:Z(t,T)~N(0,σ2(t,T)),B1(T)-B1(t)~N(0,T-t), 于是,由引理1得 (7) 再计算V2, (8) 将式(8)中的两项分别记为V21,V22,则V21与V1的计算方法相同,可得: (9) 由式(5)可得 (10) 将V1,V21,V22分别代入V(t,T,r(t),St)中,得 V(t,T,r(t),St)=2 预备知识
2.1 分离交易可转债的构成要素
2.2 分离交易可转债的价值
2.3 混合分数布朗运动的定义
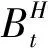
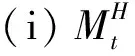
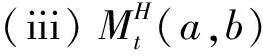
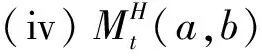
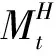
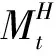
3 混合分数布朗运动下分离交易可转债定价的金融市场模型
3.1 模型假设
3.2 金融市场模型
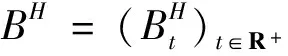
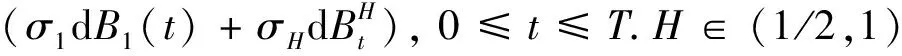
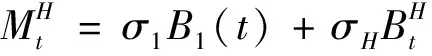
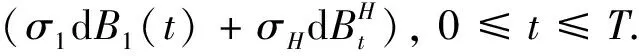

3.3 引理1 随机微分方程(1)的解为:对t≤u≤T,有
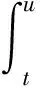
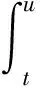
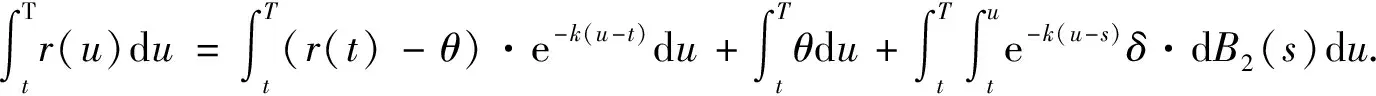
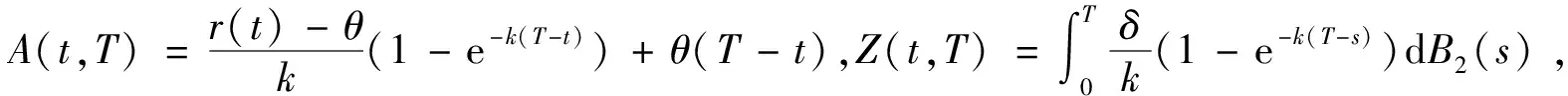
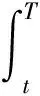
4 分离交易可转债价值的主要结论
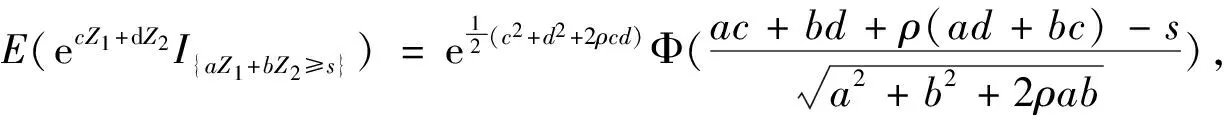

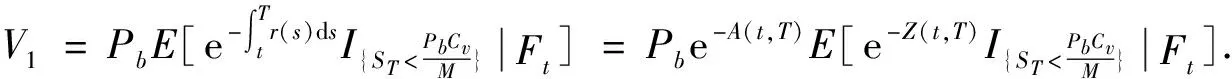
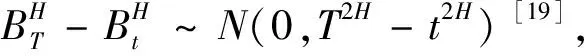
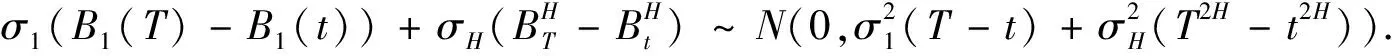
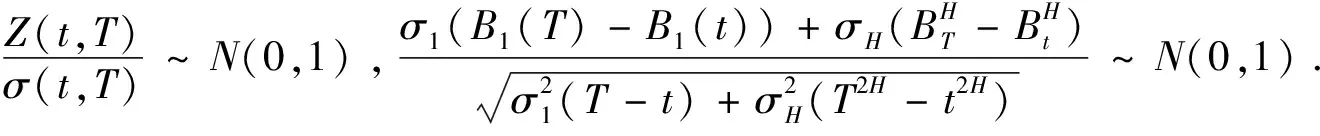
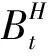
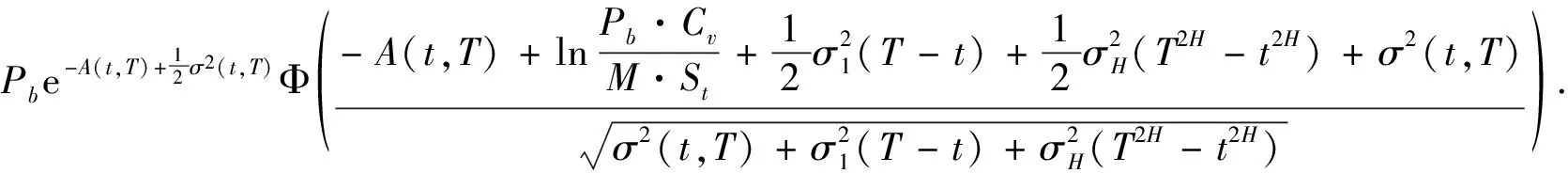
——基于SZH的案例研究

