Kopel寡头博弈模型的演化分析*
李 波,何启志
(安徽财经大学 金融学院,安徽 蚌埠 233030)
1 引 言
一般而言,市场结构可分为寡占、多寡头以及完全竞争三种形式.目前常见的产业结构存在方式多为多寡头形式,尤其是双寡头市场结构,比如饮料产业中的百事和可口、航空制造业的波音和空客等.大量的研究表明简单预期假设下的企业竞争演化路径具有相当高的复杂性,为了在公司管理层面进行竞争策略的优化,经济学家在简单预期假设基础上提出了适应性预期,即通过对历史产量进行加权平均得出当期的产量预期.进一步,假设处于竞争状态的两家企业总成本变化对彼此影响程度不对称可以构造更符合人类决策行为特点的双寡头模型,这一模型更符合认知心理学相关领域对经济实践中企业竞争现象的研究成果.研究者借助于非线性动力系统理论考察均衡状态下企业竞争行为的可能性,比如均衡点的周期性及其彼此之间的演化路径等问题.比如Zhang和Gao(2019)[1]基于外推预测技术构造了非线性Cournot寡头模型并发现弱预测技术下富有理性的调整机制意味着更倾向于收敛非对称平衡点.常建伟等(2017)[2]研究了在企业环境行为监管中,利用演化博弈理论建立了一个带有不同诉求的主体的动态模型,结果发现动态惩罚控制方法将有利于排污企业做出污染物处理的最优策略选择.
当前利用非线性动力学理论和动态博弈研究寡头竞争的模型主要集中在管理授权、预期假设和市场信息获取及分析能力等方面.随着职业经理人的出现,公司的所有权和管理权出现分离,此时公司发展的动力将不完全是利润最大化.Wu和Ma(2015)[3]研究了部分私有化与交叉持股状态下混合双寡头博弈情形下的复杂动力学行为,尤其是涉及管理授权中的委托代理理论.Gori等(2017)[4]构造了一类基于市场收益奖励机制下产品差异化对于竞争状态影响的Cournot寡头竞争模型,研究表明一般均衡点可能会不存在,需要引入更复杂的均衡结构.通常假设公司可以获知完全信息从而做出合理预期,显然这在真实的经济环境中是不可能存在的.即使公司能获知完全信息,而要做出最优预期也需要有强大的分析和计算能力以及巨大的成本耗费.基于可变成本的信息,Ma和Ren(2018)[5]研究了两阶段决策的双寡头博弈的动力学性质,尤其是可变成本对寡头竞争中主从关系这一竞争模式的影响.在理性预期选择方面,Wei和Yu(2014)[6]研究了有界理性条件下双寡头模型的动力学行为,讨论了均衡的存在性和稳定性问题,由此得到了周期倍增演化轨道和多均衡状态.相关研究结果说明竞争者对产品总量的调整速度会影响均衡的稳定性,并且证明双寡头竞争者各自的预期对寡头模型的动力学行为有重要影响.更多关于企业竞争策略选择中预期管理方面的研究结果表明理性预期选择并无简单的好坏之分,具体情况与处于竞争状态的其他企业预期选择密切相关,两者之间的策略互动情况将决定企业竞争行为的具体演化过程.Andaluz 和Jame(2016)[7]考虑了有界理性下Cournot-Bertrand类模型的动力学行为,尤其是研究了倍周期诱导出混沌这一现象.
离散Kopel双寡头模型是一类比较重要的寡头垄断模型.Canovas和Munoz(2018)[8]重点探究了系统在一维不变子集上的拓扑混沌行为,并通过拓扑熵和最大李雅普诺夫指数的计算进行了验证.
这里将重点探究模型平衡点失稳情形下的动态性质,从而讨论对称Kopel双寡头模型的复杂动力学及其演化现象.首先借助稳定性理论给出稳定性分析的结果,其次通过构造(广义)特征向量和伴随特征向量计算临界规范型及其对应的系数并在此基础上讨论1∶4共振的存在性与相关结果,最后借助数值模拟手段演示理论分析结果所蕴含的复杂的动力学性质.
2 Kopel双寡头模型及其稳定性
考虑式(1)所示的离散Kopel双寡头模型.
(1)
其中x,y分别为市场中两个寡头企业的产量,ρ,μ均为正常数,分别用来衡量市场上产量变化的权重和竞争对手产量变化对生产成本函数影响的程度.
注:模型(1)中所有变量均已做无量纲化处理.
具体而言,模型(1)中的两个寡头企业是基于有限信息做出产量调整的决策,其中产量调整是对自身产量和竞争对手产量的函数加权后求和的.这里采用非线性logistic函数估计竞争对手产量对自身的影响,更进一步的推导和解释见Canovas和Munoz(2018)[8].
对于模型(1),当参数(ρ,μ)变化时映射(1)的不动点的个数和稳定性都会发生变化.显然平凡不动点(0,0)会一直存在,但该点因没有经济学意义而不被分析.
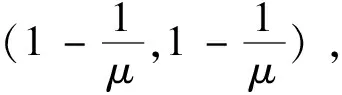
当μ≥3,映射(1)存在一组对称不动点E1(x1,y1)和E2(x2,y2),其中
关于以上不动点的稳定性分析可见文献(Puu,2018).当映射(1)的不动点处的Jacobian矩阵特征值的模等于1时,映射(1)在不动点处可能出现叉式分支、flip分支、Neimark-Sacker分支这三类单参数分支.与此对应的将出现不动点的湮灭、倍周期、拟周期和混沌现象.在已有叉式分支、flip分支和Neimark-Sacker分支定性分析的基础上研究双参数分支中的1∶4共振分支.针对Neimark-Sacker分支退化情形进行分析,可以得到1∶1,1∶2,1∶3和1∶4共振四类情形.而1∶1,1∶2,1∶3共振三类情形过于平凡不予分析,1∶4共振发生时满足的条件和其共振点邻域内的复杂动力学性质成为重点分析的对象.
3 Neimark-Sacker分支分析及其广义情形1∶4共振
第一步特征值分析给出分支存在的可能性
映射(1)在不动点E1(x1,y1)处的Jacobian矩阵为
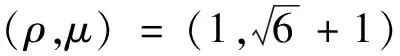
映射(1)可以通过如下方式平移不动点到原点,(x,y)=(u+x1,v+y1),此时映射(1)转变为映射(2).
(u,v)T→Δ(x1,y1,ρ,μ)(u,v)T+H(u,v),
(2)
其中H(u,v)=-ρμ(v2,u2)T.
第二步构造特征向量及其伴随特征向量并在此基础上求解其规范型
选取p,q∈2作为Δ(x1,y1,ρ,μ)的(广义)特征向量和(广义)伴随特征向量.此时,可以对整个状态空间进行特征子空间分解并计算一定条件下的临界特征子空间及其临界分支参数.在2空间,选取
其中
并且有
此时存在ω∈2,使得映射(2)在新坐标下可以表示为映射(3).
(3)
其中
第三步计算其临界系数并论证1:4共振分支存在的条件
此时可以构造坐标变换零子化映射(3)中的部分二次项和三次项,最终系统可变为如下形式(这里仍用ω作为坐标变量),
其中
以上分析说明映射(1)在不动点E1(x1,y1)处可能出现1∶4共振现象.
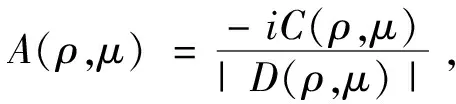
(1)对映射(1)的一组非平凡四周期不动点而言,存在一条fold分支曲线.当参数在分支曲线邻域内变化时,不动点将消失或出现倍增的情形;
(2)映射(1)在情形(1)中的不动点处出现Neimark-Sacker分支.
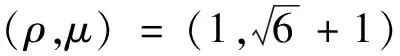
4 数值模拟
基于有限信息下相似竞争行为假说的理论,使用MATLAB软件对双寡头企业竞争行为进行仿真模拟,分别考虑三种竞争情形下的博弈结果及其相关演化性质.
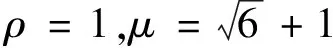
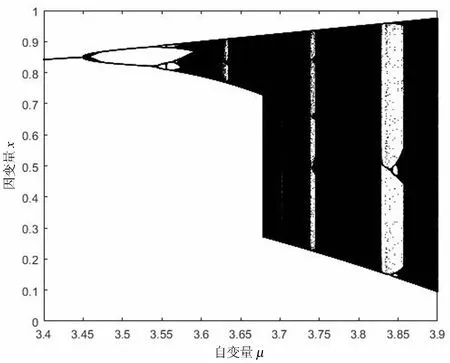
图1 固定时的分支图
由图2可知竞争对手企业的影响因素越大,双方企业的动力学行为越倾向于复杂,其动力学由严格收敛于平衡点到收敛于固定轨道,直至最后处于混沌状态.
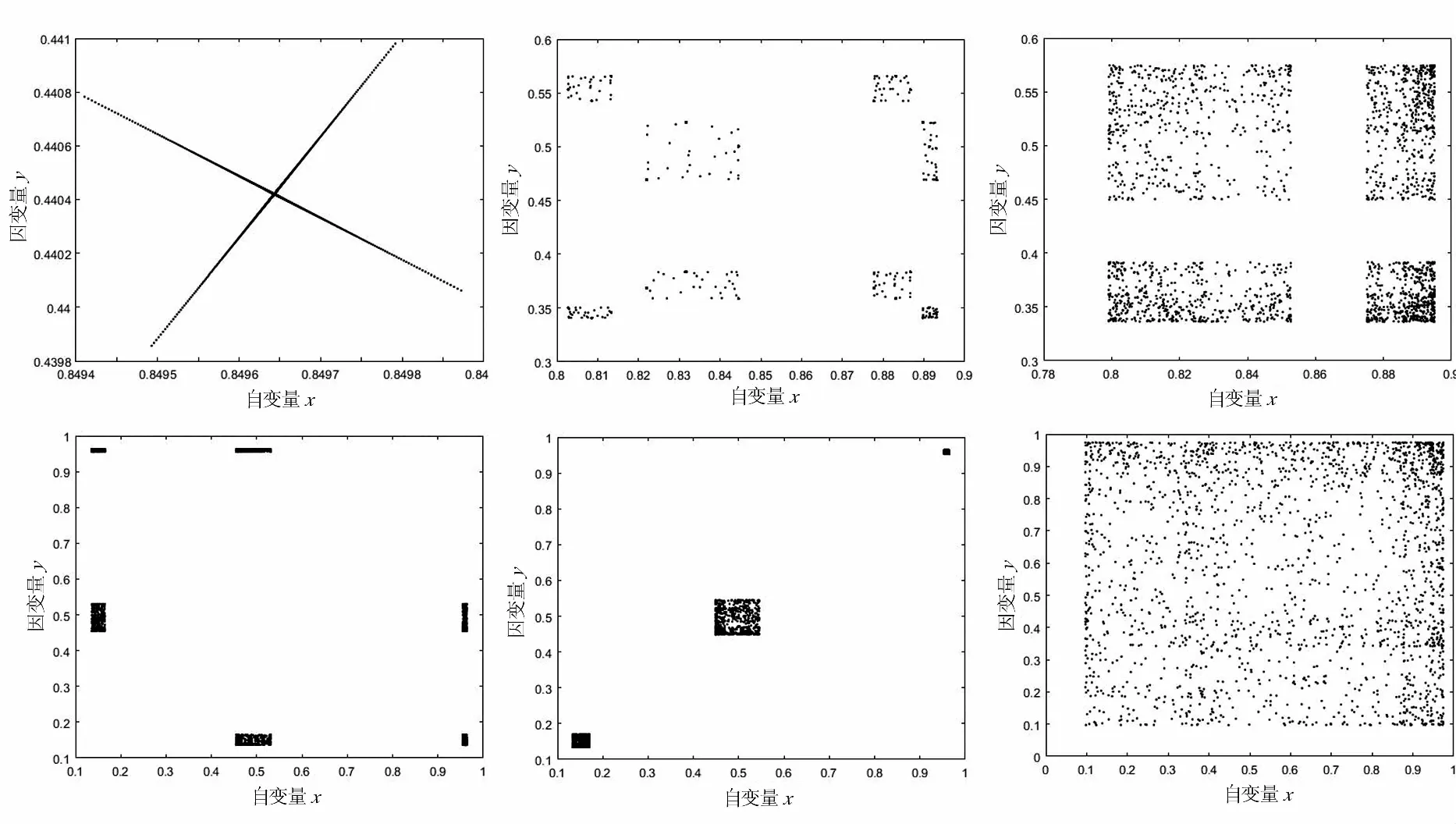
图2 映射(1)在ρ=1,μ∈[3.4,4]情形数组合下的相图
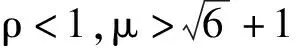
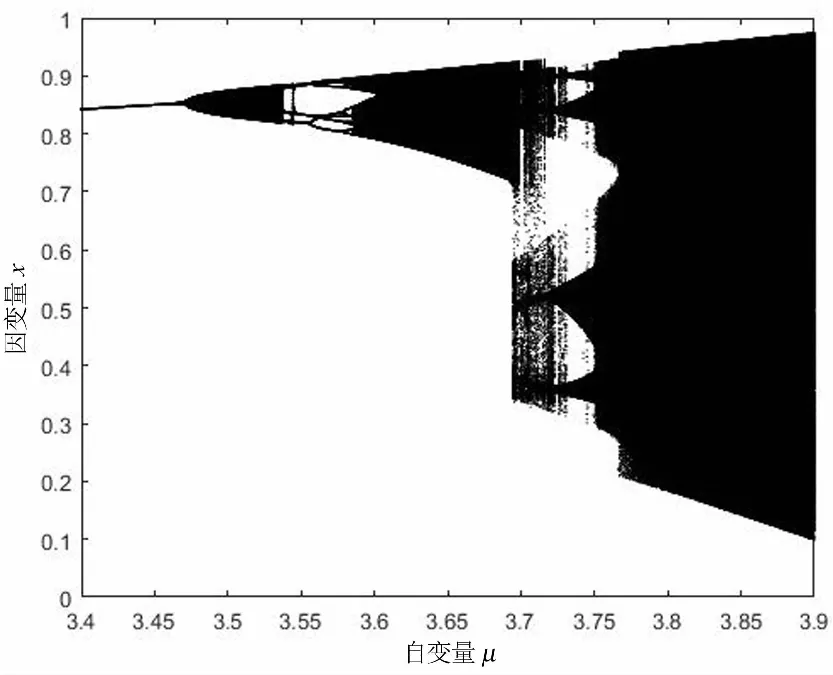
图3 固定时的分支图
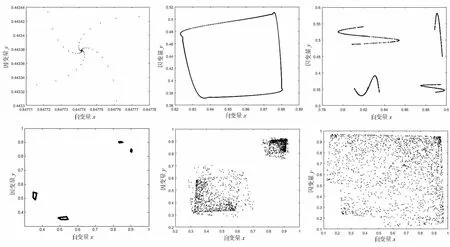
图4 映射(1)在情形数组合下的相图
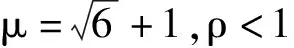
图6表明在一定参数条件下映射(1)存在一个内发散外收敛的不变闭轨道,并且随着ρ的变化闭轨道破裂称为11个具有类似性质的闭轨道,最后闭轨道全部破裂生成一个“靴子”形状的混沌吸引子.
在讨论以上三类动力学性质时都涉及了混沌现象.通过计算最大李雅普诺夫指数的方法进行验证.图7的三个指数图分别为对应图1、图3和图5的最大李雅普诺夫指数图.
对比图7和图1、图3和图5可以发现三类动力学行为都存在稳定区域、准周期区域以及混沌区域.
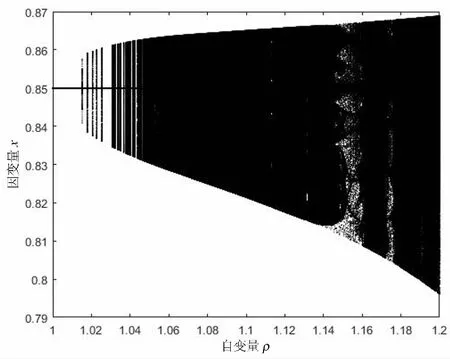
图5 固定时的分支图
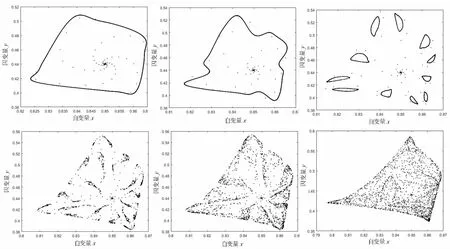
图6 映射(1)在情形数组合下的相图
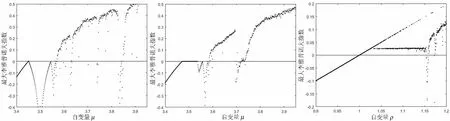
图7 最大李雅普诺夫指数图
5 结 论
在已有Kopel模型的分支结果的基础上对Neimark-Sacker分支的广义情形1∶4共振问题开展了研究.研究结果表明,当(ρ,μ)满足定理1所给条件时,Kopel模型将在一类非平凡不动点处出现1∶4共振现象.该现象的出现意味着fold分支、Neimark-Sacker分支及同宿轨道的出现.
数值分析说明一定程度上映射(1)的相图可以做90°旋转而不变,即出现4对称,这也是1∶4共振所蕴含的特有性质之一.当ρ=0.95(<1)时,企业综合考虑历史产量对当期产量的预期并赋予自身历史产量更大比重.当ρ=1时,即企业完全不考虑自身历史产量所产生的影响,仅仅调整竞争对手对自身未来预期产生的影响程度.在这两种情形下对于处于竞争中的两个企业而言存在产量上的多重均衡点,但始终在一个可预测的轨道之中.甚至在一定参数区间内当任何一方企图打破平衡时,均衡点也始终处于一个可预测的轨道之中.当ρ>1时,映射(1)出现了不同于此前的现象,即产量的不同调整方向趋向于同一类均衡状态,出现同宿现象.此时意味着同时存在多个均衡状态,企业竞争策略的调整仅仅在不同状态之间转移,竞争双方极有可能呈现出事实上的共谋情形.此外,与初始状态无关,映射(1)始终存在参数区间使双方的竞争处于混沌状态,这是一种不利于双方企业获取可能的最优利润情形.

