基于ARMA模型的共享单车的投放预测与管理*
何郁波,曾 桢,兰燕鸿,黄遵杰
(怀化学院 数学与计算科学学院,湖南 怀化 418008)
1 引 言
在移动互联网和智能手机APP等创新技术的驱动下,城市慢行交通领域作为一种新型事物逐渐出现.在城市居民的出行领域,打车类应用软件的发展逐渐趋于稳定,但民众在短途的出行中“最后一公里”出行的问题始终没有得到解决.近年来,共享单车的出现,让民众多了一种绿色的出行方式可以选择[1].共享单车的最大价值在于民众出行的“最后3公里”,其无桩借还的模式相比于政府公共租赁自行车,使民众借还单车更加快速和便捷.同时,共享单车引导政府部门重视慢行交通系统的建设,倡导民众更多选择绿色出行的方式,这些方面能在一定程度上缓解城市交通拥堵、改善城市环境.然而,共享单车作为新兴事物,随着共享单车平台企业在各大城市开始大量投放单车,共享单车的停放、安全出行等问题引起了社会的关注[1].
2 模型的基本知识
基于时间序列分析的方法,本文将对某一个定点对于共享交通工具的使用情况进行分析预测,从而为相关部门提供共享交通工具的投放与管理提供依据.所谓时间序列,就是按照时间的顺序将某种现象的某一个统计指标的数值排列而形成的序列.对时间序列进行观察、研究,寻找它变化发展的规律,预测它将来的走势.常见的预测方法有利用回归的方式建立相应的模型预测,如利用支持向量机回归、线性回归等预测方法[2];有采用径向基函数(RBF)神经网络模型对时间序列进行拟合及预测[3].
在时序分析中,求和自回归移动平均(autoregressive integrated moving average, ARIMA)模型是时间序列预测方法最为经典的模型.将具有如下结构的模型称为ARIMA(p,d,q)模型:
(1)
利用ARIMA模型对一些重要时序进行预测和应用目前已取得了大量非常重要的结果.文[4]针对工控系统现场控制层数据进行分析,利用数据的时序性,通过ARIMA模型预测出后续时刻系统数据的信息.李勃旭等运用研发的数据采集系统对新上线地铁门的夹紧力进行实时采集,对于采集后的时序数据利用ARIMA模型与EMD-ARIMA模型对夹紧力峰值的均值和标准差随累计运行时间的变化趋势进行预测,获得了非常有用的结论[5].针对烟草行业的供给,文[6]利用ARMA模型对烟草的供给和配送进行了预测.关于ARIMA模型与其他模型相结合的方法,也有诸多的文献进行了研究.王涛采用ARIMA模型、BP神经网络模型和Holt指数平滑模型对1995-2017年上海电力需求数据进行建模分析,构建了组合模型,并依据组合模型预测了未来五年的上海市电力需求量趋势[7],拟合的效果较好,有利于电力供应单位稳定电力供应,促进经济社会发展.同时,结合ARMA和GARCH建立预测模型的成果表明:在拟合效果上,ARMA-GARCH模型较优;在预测效果方面,ARMA模型最优[8].其他一些相关的成果可参阅以上所列的文献及其中所介绍的相关参考文献.
3 数据预处理
数据预处理及相应分析的流程图如图1所示.以湖南省怀化市第一人民医院为观测点,对2018年6月27日—2018年9月15日的观测统计,以7:30—18:30为观测时间段,共获得81天的共享单车日使用台·次,结果见表1.
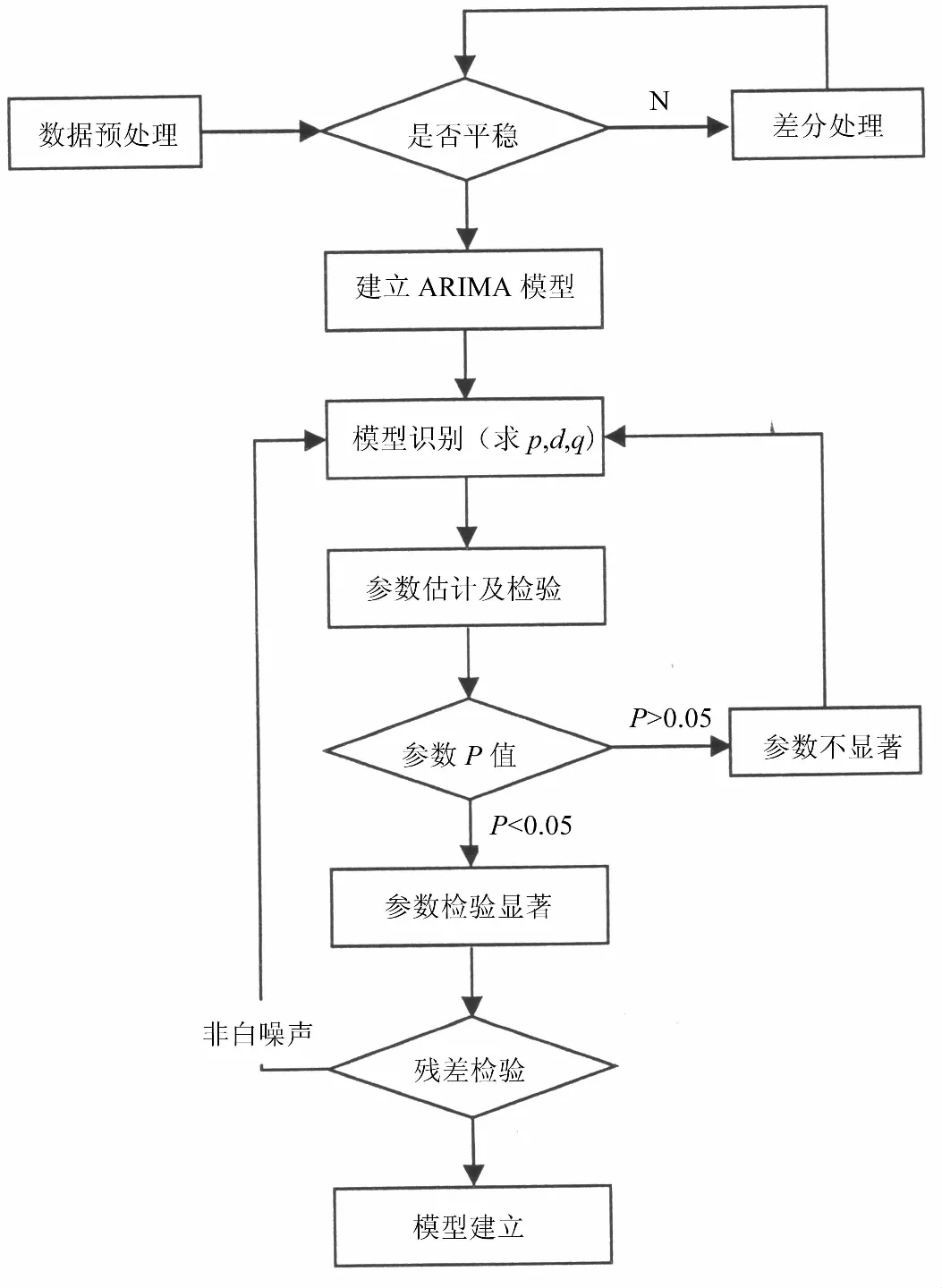
图1 确定时间序列模型流程图
将原始序列记为X-user,对序列X-user进行纯随机性检验,即白噪声检验.利用SAS软件对序列X-User进行白噪声检验结果如表2所示.表2的白噪声检验结果表明,延迟6,12和18期的χ2统计量的相伴概率都小于显著性水平5%,因此原序列X-user属于非白噪声序列,具有相关性.

表2 白噪声检验结果
序列X-user的时序图见图2,由时序图可知该序列是平稳序列,均值为52.6667,标准差18.3397.
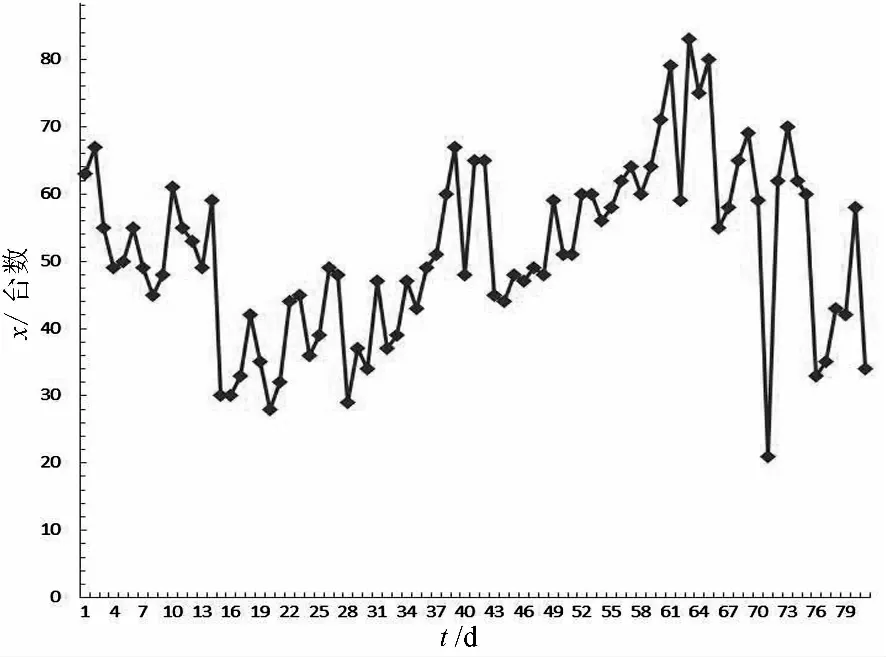
图2 原始序列的时序图
4 模型的建立与预测
为了对模型进行识别并定阶,采取对序列的自相关以及偏自相关的拖尾或截尾的性质来进行判别.利用SAS对X-user序列进行分析,自相关和偏自相关系数图3.

图3 序列X-user的自相关图
由自相关图可知序列X-user的自相关图延迟1期以后虽然在2倍标准差的范围之内,但是一直到延迟12期自相关系数保持一定的拖尾性.图4序列X-user的偏自相关系数在延迟1期以后出现截尾性,因此尝试拟合AR(1)模型.

图4 序列X-user的偏自相关图
使用条件最小二乘估计方法,确定AR(1)模型的口径为
(2)
且Var(εt)=299.6057.
残差的白噪声检验显示延迟6阶、12阶、18阶、24阶所对应的LB检验统计量的P值均显著大于0.05,所以该AR(1)模型是显著有效的.

表3 残差的白噪声检验结果
对参数的显著性进行检验,结果显示两参数t统计量的P值都小于0.05,因此两个参数都显著.因此AR(1)模型是序列的有效拟合模型.

表4 条件最小二乘估计结果
为了更好地拟合原始序列,搜索最优的模型.通过序列自相关图2显示,该序列自相关系在5阶以后表现一定的截尾性,另外偏自相关系数带一定的拖尾性,因此考虑用MA(5)模型进行拟合.同样采用条件最小二乘法对相关参数进行估计,得到MA(5)模型口径为
X-usert=52.71613+(1+0.35179B+0.07076B2+0.06588B3+0.16252B4+0.18323B5)εt且Var(εt)=300.9124.
残差的白噪声检验结果显示拟合的模型显著有效,另外对于参数进行显著性检验结果为所有待估的参数均显著.
为了比较两个模型的优劣性,引入AIC和SBC信息准则.检验结果如表5.

表5 拟合模型的AIC和SBC信息准则结果
最小信息量的检验显示,AR(1)模型无论使用AIC准则还是SBC准则均优于MA(5)模型.为了避免漏掉最优的模型,我们采用在IDENTIFY命令中增加一个可选命令MINICp=(0:5),q=(0:5),获得原始序列中所有自相关延迟阶数小于等于5,移动平均延迟阶数也小于等于5的ARMA(p,q)模型.
由表6的最小信息准则结果可知,在自相关延迟阶数和移动平均延迟阶数小于等于5的所有ARMA(p,q)模型中,BIC信息量相对最小的是BIC(1,3)=5.720673,即ARMA(1,3)模型.采用条件最小二乘估计,各参数的估计值结果见表7.估计结果显示,所有的参数均显著(t检验统计量的P值均小于0.05).

表6 最小信息准则结果

表7 ARMA(1,3)模型参数的条件最小二乘估计结果
新模型ARMA(1,3)的残差自相关检验结果表8显示,由于延迟各阶的LB统计量的P值均显著大于α(α=0.05),所以该拟合模型显著有效.

表8 ARMA(1,3)模型的残差自相关检验结果
拟合模型为
(3)
根据上述所得模型,利用SAS软件对第82,83,84,85,86期共5期怀化市第一人民医院共享单车的使用进行预测,预测结果和实际的观察结果如表9所示.

表9 共享单车的短期预测结果
从表9的预测结果与实际值的比较可知,模型对于短期的预测具有较高的吻合度,共享单车日使用台数预测95%的置信区间很好的包含了实际值.具体的预测结果见图5.图中实线所显示的为预测值,虚线所夹部分为置信水平为95%的置信区间.

图5 共享单车日使用台数预测的95%置信区间结果
4 结 论
采用ARMA模型对2018年6月27日—2018年9月15日期间某一固定地点共享单车的使用数据进行建模分析,利用SAS软件对所建立模型的有效性、参数的显著性进行了检验,从而获得了共享单车使用所满足的模型口径.利用训练样本和检验样本对所建立的模型进行了检验,结果表明所建立的模型拟合效果较好,短期预测精度较高,从而对管理部门的投放和管理工作提供了可靠的依据.

