初中数学复习中“概念图
——题组教学”模式——以三角形的内角平分线定理的证法为例
福建省石狮市华侨中学 郑惠容
2017 年泉州中考模拟卷3 的第22 题是一道证明三角形内角平分线定理的题目,考完之后,发现很多学生都不会证明。学生不会证明的原因在于没有熟练掌握成比例线段的基本方法,不懂得把它转化为相似三角形的基本模型进行解决。其实只要学生懂得转化,要解决这样的问题就易如反掌了。那么,证明成比例线段有哪些最基本的模型呢?
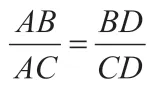
。
分析:要证明四条线段成比例,常用的方法是证明三角形相似,但在本题中我们发现,以线段AB、BD、AC、CD 为边所构成的两个三角形△ABD 与△ACD 是不相似的。那么如何证明这四条线段成比例呢?下面将对本题的解法做以分析。
思路一:转移线段法
由于这四条线段所在的三角形不相似,可都考虑“移”其中的一条线段,达到构造两个相似三角形的目的。
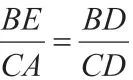
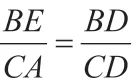
证法1 和证法2 是通过作平行线来“移”线段AB 和线段AC。其实,也可以把它们“移”到射线BA、CA 上来,构成熟悉的“A”型或“X”型相似。我们也可以考虑“移”线段BD 或线段CD。
以上两种证法的思路都是“移”四条线段中的一条线段,从而转化为相似三角形的基本模型“A”型、“X”型相似。
思路二:寻找“中间比”
除了上述的“移”法外,寻找“中间比”也是常见的证明线段成比例的方法之一。
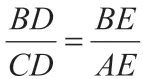
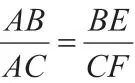
思路三:利用割补法
与三角形的全等类似,我们也可以采用“以大割小”或“以小补大”的思想来构造三角形相似。而“移”线段其实也是一种“割补”的思想,那么还有其他“割补”的方法吗?
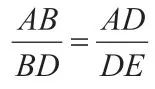
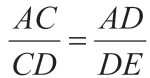
【思考】如图8,想一想:如果AD 是△ABC 的外角平分线,与BC 的延长线交于点D,那么是否还可以得出与内角平分线类似的结论?如果有,如何证明?你是否可以用类比三角形内角平分线定理的证明方法的思想中得出某些启发?
你可以动手试试看,就会发现,证明三角形内角平分线定理的几种方法均可用于证明三角形外角平分线定理,在这里,就不再重复叙述。
本文只涉及一道题目,但复习了证明比例式的基本思想与方法,构造基本的相似三角形:“A 型”或“X 型”(两角对应相等,两三角形相似);平行线分线段成比例定理;通过寻找中间比进行证明。诱发一题多解的方法很多,教师应根据问题的特点,结合学生的实际,遵循学生的认知规律,适时加以点拨与引导,促使学生运用不同的解题思路去解决问题。

