Singularity radius gradient-based rapid singularity-escape steering law for SGCMGs

Tao YI, Yunhai GENG, Baolin WU

Research Center of Satellite Technology, Harbin Institute of Technology, Harbin 150080, China

KEYWORDS Gaussian curvature;Rapid singularity escape;Single gimbal control moment gyroscope;Singularity-escape steering law;Singularity parameter;Singularity type

Abstract In order to visualize singularity of SGCMGs in gimbal angle space, a novel continuous bounded singularity parameter--Singularity Radius,whose sign can distinctly determine singularity type, is proposed. Then a rapid singularity-escape steering law is proposed basing on gradient of Singularity Radius and residual base vector to drive the SGCMG system to neighboring singular boundary, and quickly escape elliptic singularities. Finally, simulation results on Pyramid-type and skew-type configuration demonstrate the effectiveness and rapidness of the proposed steering law.

1. Introduction

Owing to a remarkable advantage of torque amplification capability, Single Gimbal Control Moment Gyroscope(SGCMG) is considered as an efficient actuator for longtime running of spacecraft. However, singularity, as an inherent problem of SGCMG, seriously affects the performance of SGCMG system and hampers its application in attitude control1,2of spacecraft. In the past four decades, substantial progress has been made in singularity theory and steering law.

In the field of singularity theory, Magulies and Aubrun3calculated angular momentum of SGCMGs based on singular direction to visualize singular surfaces in angular momentum space, introduced the concept of null motion and analyzed the passability of singular states. Kurokawa4studied the relationship between tangent space of singular surface and null motion space in depth, and demonstrated that base vector of singular surface and null motion can fill up the whole gimbal angle space in nondegenerate states. In addition, Kurokawa derived the expression of Gaussian curvature and provided corresponding rules to distinguish singularity type. Wie5presented another singularity analysis method based on Binet-Cauchy identity which can also visualize singular surfaces,and further derived two fundamental forms of differential geometric theory in singular surface. Yamada and Jikuya6introduced a concept of directional passability, and analyzed its property in singular surfaces through comparison with passability. Kojima7gave the necessary and sufficient condition of boundary of elliptic and hyperbolic singularity, calculated the specific gimbal angles of boundaries and applied curve fitting method to gain practical expression of boundaries. Geng et al.8proved that degenerate states correspond to boundaries of different singularity types and introduced mean curvature of singular surface to improve the Gaussian curvature-based singularity discrimination method.

To realize attitude control of spacecraft,steering law which allocates commanded torque to each SGCMG has been extensively studied.In general,steering laws can be divided into two types: singularity-avoidance steering law and singularityescape steering law.Singularity avoidance steering law usually employs optimization algorithms to realize singularity avoidance, while singularity-escape steering law attempts to escape hyperbolic and elliptic singularity under the guide of singularity parameters. In the field of singularity-avoidance steering law, Vadali et al.9gained appropriate initial gimbal angles through back integration from desired momentum to zero momentum for specific directions,and guaranteed a nonsingular maneuver. Paradiso10applied a guided depth-first search method to optimize coefficient of null motion to avoid singularities. Kurokawa11,12restricted the whole angular momentum envelope of pyramid-type configuration by adding a constraint equation to gain a nonsingular angular momentum space. Takada et al.13presented a surface cost function through off-line calculation of singular surfaces to realize semi-global singularity avoidance. Kusuda and Takahashi14applied Fourier series to fit torque command to optimize the trajectory of gimbal angles. Zhang et al.15utilized dual-mode model predictive control and Gauss pseudospectral method to acquire adequate gimbal rate vector. Geng et al.16derived an analytical expression of nonsingular gimbal angular velocity trajectory under the condition that the trajectory of commanded torque is given. In these methods, the singularity avoidance is realized at the cost of requiring large amount of calculation and memory capacity or sacrificing partial angular momentum space which limits their practical applications.

As to singularity-escape steering law, Bedrossian et al.17,18classified gimbal angles with sign of Jacobian minors, and introduced singular robust inverse steering law which balances torque error and gimbal rates in singular states and gradient steering law to escape hyperbolic singularity by null motion.To further reduce torque error, Ford and Hall19introduced singular value decomposition method and proposed a singular direction avoidance steering law.Wie et al.20revised the singular robust inverse steering law to be Generalized Singularity Robust Inverse (GSRI) steering law that perturbs the output of gimbal rate when the system comes across‘gimbal lock’situation, and proposed an off-diagonal steering law21to solve the problem of escaping from saturation singularity. Leeghim et al.22proposed a singularity measurement parameter,namely inner product, a predicted singular robust steering law with one-step ahead singularity index, and further applied it in a hardware-in-the-loop simulation.Wu et al.23introduced space expansion method to expand Jacobian matrix into ndimensional square matrix, analyzed the corresponding singularity and further proposed a hybrid steering strategy. Valk et al.24analyzed the difference between internal elliptic singularity and saturation singularity, and proposed a singularity escape and avoidance steering law on the basis of a series of parameters which describe angular momentum capacity in direction of commanded torque.Besides,to escape elliptic singularity rapidly, Geng et al.8introduced an idea that escapes singularity by driving the SGCMG system to the nearest boundary in angular momentum space and designed an elliptic singularity-escape steering law. Guo et al.25generalized the strategy of Geng et al.8to avoid the discontinuity problem of singular surface in angular momentum space,and proposed a steering law that would drive the system to the closest boundary in gimbal angle space. Although the singularity-escape steering law proposed in Refs.8,25 can drive the SGCMG system to quickly escape from elliptic singularity,data of angular momentum or gimbal angles in singular boundaries needs to be stored in advance and additional calculation is required to search the nearest point of boundary.

Since elliptic singularity is impassable by null motion, the quickest way to escape elliptic singularity is sliding on singular surface in gimbal angle space and heading for neighboring singular boundary. Thus, singularity parameter in singular states is needed to guide the process of escape. As the only known parameter that can determine singularity types, Gaussian curvature may have the same sign in different types of singularity and its value goes to infinity in singular boundary,7which make Gaussian curvature cannot be an appropriate singularity parameter to describe the nature of singular states. To deal with this problem, this paper proposes a novel continuous bounded geometric parameter-singularity radius, which can visualize the singular degree of singularities for all SGCMG systems. The geometric expression of singularity radius is derived to further understand its difference from Gaussian curvature, and the corresponding singularity discrimination method is proposed. According to its geometric expression, it is easily known that singularity radius has the same sign in the same type of singularity for all singular states. Then, to realize a rapid escape from singularity, the steepest gimbal angle velocity which makes singularity radius decrease fastest in singular surface is derived based on gradient of singularity radius and singularity analysis method.However,the SGCMG system may fall into an infinite loop of escaping singularity and entering singularity when the escape strategy is chosen as driving the SGCMGs to directly escape from hyperbolic singularity. Hence, the residual vector in singular boundary is employed to steer the system to escape elliptic singularity from the boundary. Combining the steepest gimbal angle velocity with the residual vector, an analytical singularity radius gradient-based steering law is designed to realize a rapid escape from elliptic singularity. Finally, simulations on pyramid-type configuration and skew-type configuration with five SGCMGs have been carried out to demonstrate that the proposed steering law can quickly steer the SGCMG system to singular boundary, and it costs less time in escaping elliptic singularity than several typical steering laws.

2. Singularity theory of SGCMG system

This section reviews the basic theory about SGCMG system including the definitions of singularity,singular surface,elliptic singularity and hyperbolic singularity, and then introduces geometric parameters-Gaussian curvature and mean curvature, and a singularity analysis method proposed by Wie.5

2.1. Singularity and singularity type of SGCMG

For an SGCMG system,the whole angular momentum can be described as where Hcmgis the total angular momentum of all SGCMG,h0is the angular momentum amplitude of each SGCMG,hiis the angular momentum vector of the ith SGCMG, and n is the number of SGCMGs.

Taking the derivative of Hcmg, torque generated by SGCMGs can be expressed as

where δ=[δ1, δ2,......, δn]T, δiand ˙δirepresent the gimbal angle and gimbal angular velocity of the ith SGCMG respectively,A=[t1,t2,......,tn]is the Jacobian matrix,tiis the unit torque vector of the ith SGCMG, and Tcmgdenotes the total torque generated by SGCMGs.

When rank(A)=3,the SGCMG system can precisely provide three-dimensional real-time commanded torque. However, when rank(A)=2, it loses the ability to generate torque in one direction - the so-called singular direction u,and these situations are called singularity. Curved surfaces formed by the total angular momentum Hcmgof all singular states in angular momentum space are named as singular surfaces.

To distinguish different types of singularity,null motion δNis introduced. It is defined as certain gimbal angular velocity vectors that would not change the whole momentum of SGCMGs.For a theoretical continuous SGCMG system,null motion δcNshould satisfy the following constraint:

where ΔHcmg=Hcmg(δ+dδ)-Hcmg(δ) represents the variation of angular momentum during a sampling period,H(δ)=[h1, h2,......, hn] is the angular momentum matrix, cos dδ=[cos dδ1, cos dδ2,......, cos dδn]T, sin dδ=[sin dδ1, sin dδ2,......, sin dδn]T, and 1=[1, 1,......, 1]T.

Analytical solution to Eq. (5) is not available and it is difficult to analyze the properties of corresponding null motion.To simplify solving process, Taylor series expansion method has been employed,high order terms has been omitted and null motion δdNis restricted to satisfy Eq. (3). Then, the projection of ΔHcmgonto u,u·ΔHcmg,which determines the type of singularities, is expressed as

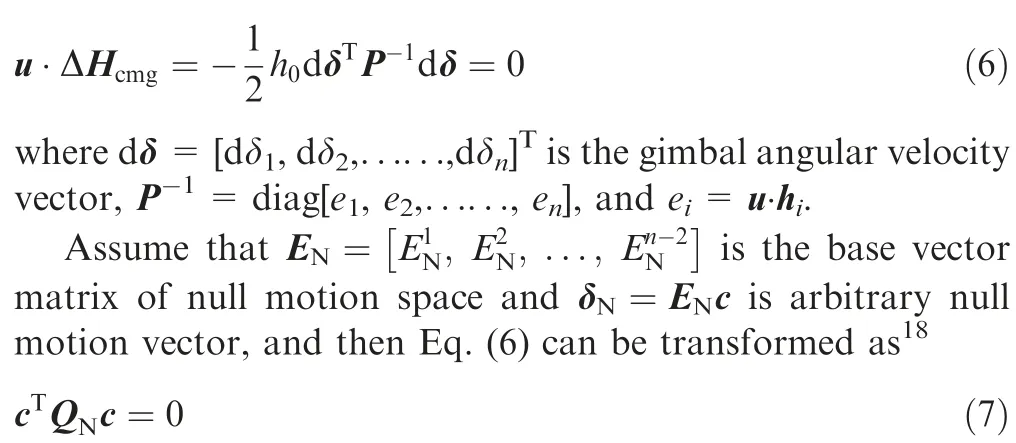
where QN=ETNP-1EN, c is the coefficient vector of null motion.

If QNis sign-definite, the unique solution of Eq. (7) is c=0, and thus no nonzero null motion vector make Eq. (7)equal. The corresponding singularity cannot be escaped by nullspace vector of A, and it is called elliptic singularity. If QNis indefinite, the corresponding singularity is called hyperbolic singularity.In this case,null motion is an effective way to steer SGCMGs away from singularity except for degenerated situations.

Another way to distinguish the types of singularity is based on differential geometric parameters-Gaussian curvature κ introduced in Ref. 3) and mean curvature υ referred in Ref.8, which can be expressed as

where |titju| represents determinant of the matrix formed by vector ti, tjand u.

It is assumed that ε is the sign vector of e, and its elements satisfy εi=sign(ei). Since sign vector ε does not change with the transformation of base vector in tangent space,4the sign of eigenvalue of matrix QNcan be derived by combing ε with sign of Gaussian curvature and mean curvature. Then, singularity type can be easily determined by whether matrix QNis sign-definite or not.

2.2. Singularity analysis in gimbal angle space

To find new method to visualize singular surface in angular momentum space, Wie5proposed a singularity analysis method based on Binet-Cauchy identity for pyramid-type SGCMG system through which singular surface can be calculated by two chosen gimbal angles.As a commonly used singularity measurement parameter, D can determine whether SGCMG system is in singular state or not. It is defined as

where Miis the ith three-order compliment minor of Jacobian matrix A.

For SGCMG systems, singularity condition can be expressed as D=0 which is equivalent to Mi=0.Then,constraint equation among arbitrary three gimbal angles can be obtained,5which is

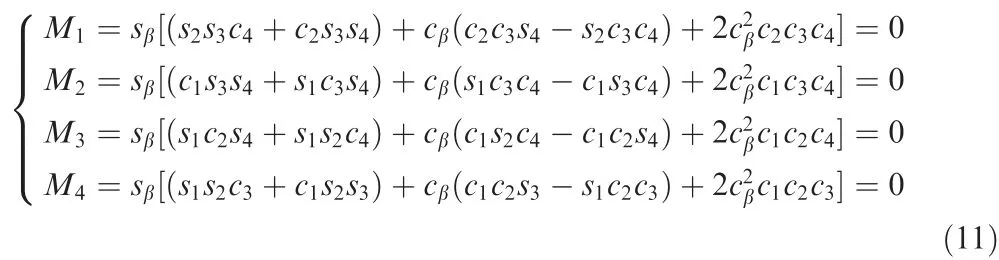
where si=sin δi, ci=cos δi, and β is the skew angle of pyramid configuration.

Hence,by combing any two equations,gimbal angle vector δ and the whole angular momentum Hcmgof SGCMG system can be denoted as functions of arbitrary two gimbal angles.These chosen two gimbal angles are also called as independent variables. Without loss of generality, δ1and δ3are chosen as the independent variables,and then δ2and δ4can be expressed as

There are four kinds of combinations as shown above due to the property of arc tangent function; nevertheless, when both numerator and denominator of arc tangent function equal zero, values of δ2and δ4obtained by Eqs. (12)-(15)are not correct. The corresponding cases are listed as

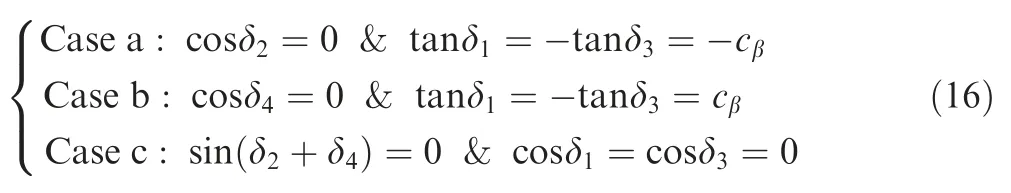
The calculated result of δ4is wrong in Case a which corresponds to the special situation u//g4,while the calculated result of δ2is wrong in Case b which corresponds to the special situation u//g2.In these situations,the singular direction u parallels to gimbal vector of the 2th or 4th SGCMG, which is actually the boundary of singular surfaces with different sign vector ε. As to Case c, the calculated results of both δ2and δ4are wrong.

Therefore, only one pair of gimbal angle is inadequate to compute the total angular momentum for all singular states.Here we give an effective strategy: firstly, find three SGCMGs whose gimbal vectors are linearly independent in angular momentum space; secondly, select two SGCMGs, whose gimbal angles can correctly calculate other gimbal angles,from the three SGCMGs. For instance, a list of feasible independent variables is (δ1, δ3), (δ1, δ2), (δ2, δ3), and the proper independent variables for current gimbal angle vector can be found by checking the list one by one.In fact,if the linearly independent gimbal vectors can be found, the applicable pair of independent variables always exists.

However,singularity condition is satisfied for any SGCMG system with any number of SGCMGs. Thus, in general, the singularity analysis method can be implemented by two steps:

Firstly, find two adequate gimbal angles, like δpand δq, as independent variables;

Secondly, express arbitrary gimbal angle δias functions of independent variables by computing constraint equation|titptq| =0.

In addition, the resulting functions δi(δp, δq) by the singularity analysis method explicitly explain the relationships of all gimbal angles in singular states, which makes it an important basis of further singularity study in gimbal angle space.

3. Singularity radius

To quantify and visualize how singularity types distribute and vary inside singular surfaces, a novel bounded parameter in gimbal angle space is proposed and analyzed in this section.

3.1. Singularity parameter

Through studies for almost half a century, several important singularity parameters have been proposed to investigate the singularity problem of SGCMG system. These parameters can be divided into two types:singularity measurement parameter and singularity description parameter. Singularity measurement parameter reflects how far the current SGCMG system is away from singularity, while singularity description parameter describes the singular degree of SGCMG system in singular states.

Up to now, only two singularity description parameters have been introduced,which are Gaussian curvature and mean curvature, and mean curvature is just used as an auxiliary parameter to distinguish singularity type. As pointed out in Ref. 7 and demonstrated in Ref. 8, the following equation is satisfied and only satisfied in the boundary of elliptic and hyperbolic singularity.

where κ denotes Gaussian curvature of singular surface in angular momentum space.

The existence of infinity makes Gaussian curvature be not suitable to visualize by figures,and the fact that Gaussian curvature may have different signs for the same type of singularity as presented in Ref. 4 makes it vague to describe elliptic and hyperbolic singularities in all singular states.

To solve these problems, a novel singularity description parameter-singularity radius Rsis proposed as

According to Eq.(18),it is obvious that singularity radius is a continuous bounded parameter in all singular states since ek,tiand u are continuous bounded variables.Although the value of singularity radius could be easily calculated and corresponding partial derivatives could be derived by Eq. (18), the basic difference between Rsand Gaussian curvature and whether Rscan be similarly used to discriminate singularity type are still not clear. Thus, a geometric expression of singularity radius is derived in the following content of this section.

In Ref. 8, Geng et al. derived the geometric expression of Gaussian curvature, which can be simplified as

where ESrepresents the base vector of tangent space of singular surface, QS=ETSP-1ES. Meanwhile, let E=［ES， EN］.Thus, E is an orthogonal matrix in nondegenerate states.

In addition,the degenerate states correspond to the boundary of elliptic and hyperbolic singularity.8As a result, in nondegenerate states, the determinant of P-1meets

while in degenerate states, Rsequals zero according to Eqs.(17) and (18), and det(QN) and det（ETSATAES） also equal zero as analyzed in Ref.8.Therefore,Eq.(21)holds for all singular states. Since QNis the fundamental theoretical matrix which describes the singularity of SGCMGs, Rsis also a geometric parameter like Gaussian curvature.

According to Eq. (21), Rsand det(QN) have the same sign since det（ETSATAES） is positive definite in nondegenerate states. Therefore, singularity radius can be used to distinguish the types of singular state just like Gaussian curvature. When n ＞4, the discrimination method is summarized in Table 1,where singular direction is chosen to satisfy the condition that ε has more 1 s than -1 s, and nεdenotes the number of -1 in sign vector ε.

As shown in Table 1,when nε=2 and the sign of Rsis positive, the type of singularity could be elliptic or hyperbolic.Under this circumstance, mean curvature is needed to assist the determination of singularity type.

When n=4, the discrimination method can be simplified as

Therefore, in 4-SGCMG system, singularity type can be easily determined by sign of singularity radius.Besides, unlike the fact that Gaussian curvature of elliptic or hyperbolic singularity changes sign in adjacent singular surfaces, singularity radius keeps the same sign for the same type of singularity which makes singularity radius a concise parameter to distinguish singularity type in all singular states.

3.2.Property of singularity radius in pyramid-type configuration

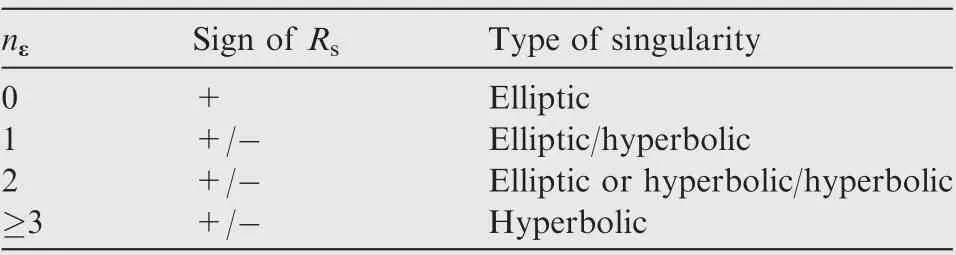
Table 1 Singularity discrimination by singularity radius.

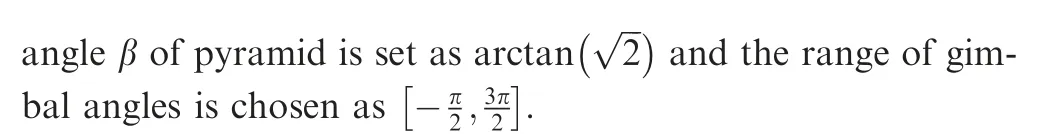
The curved surface of Rsin singular states is shown in Fig. 1. The four subfigures of Fig. 1 correspond to cases described by Eqs. (12)-(15). As illustrated in Fig. 1, Rsspans a smooth surface in all singular states. The blue contour line remarks the boundaries between elliptic and hyperbolic singularities. In Case A and D, the surface corresponds to singular states in 0H and 2H, while in Case B and C, singular states from 0H, 2H and 4H singular surfaces can be found. All singular states of pyramid-type system are shown in this figure.

According to Fig. 1, it is clear that singularity radius is a bounded parameter. The value of Rscan be obtained through mathematical computation. It ranges from 4/3 to 8/3, in 4H singularity, ranges between -4/3 and 4/3 in 2H singularity,and reaches its minimum value -8/3 in 0H singularity.Although these extreme values vary with the change of skew angle β, singularity radius still differentiates singularities with different sign vectors ε clearly. Considering the value of Rsas singular degree of singular states, it can be easily known how far the current singularity is away from boundary. Thus,through plotting curved surface of singularity, singularity radius visualizes the singular state of SGCMG system and makes the distribution of singular degree clear.

Remark 1. In Case B and C, the value of Rsbecomes a line that parallels to Z-axis in some points in Fig.1.That is caused by the incorrect case of arctangent function in Eq. (16), and these mistakes could be corrected by replacing the independent variables (δ1, δ3) with other pair of variables.

4. Gradient-based singularity-escape steering law

Since hyperbolic singularity can be escaped by null motion,escaping internal elliptic singularity becomes the most critical issue for steering laws to solve. According to the above analysis for singularity and singularity radius, the steepest gimbal angle velocity along which singularity radius decreases fastest is derived.Then a redundant vector in boundary is introduced,and a Singularity Radius Gradient(SRG)-based steering law is proposed to drive the SGCMG system to slide on singular states from elliptic singularity to the closest boundary and eventually leave singular states from the boundary.

4.1. Steepest gimbal angle velocity of singularity radius

As indicated in Ref. 4, singular surface of internal elliptic singularity is impassable. When SGCMG system happens to encounter internal elliptic singularity,the fastest way to escape from elliptic singularity is sliding on singular surface and heading for the boundary.Therefore,according to the discussion in Section 3, singularity radius could be used to guide SGCMGs toward the singular boundary.

In the view of Rs,the quickest way to leave singularity corresponds to reducing the value of Rsas fast as possible. To realize this, the gradient of Rsis required to design a rapid singularity-escape steering law. However, there is no theoretical expression of singular direction u which limits the calculation of Rsand its gradient.A simple expression of u is given for practical computation on the basis of relationship between the

where ˙δsis the time derivative of δs.

The unit vector of gimbal angle velocity ˙δ which makes Rsdecrease fastest in singular states, named as steepest gimbal angle velocity,could be obtained by seeking the corresponding ˙δsfirstly. Since ˙δspand ˙δsqform a skew coordinate system in the tangent space of singular surface, according to Eq. (26),the desired ˙δsshould be

Therefore, the desired steepest gimbal angle velocity,expressed as ˙δE, should satisfy

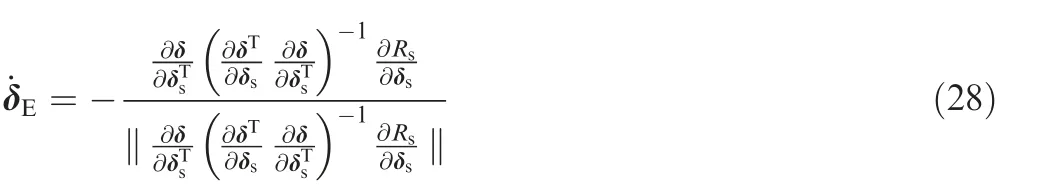
4.2. Escape strategy and steering law

A natural idea to escape singularity is steering SGCMGs under the guidance of Rs, driving the system to neighboring hyperbolic singularity and finally escaping singularity by null motion. However, due to the fact that elliptic singularity has larger angular momentum than hyperbolic singularity in the same piece of singular surface,this strategy might trap the system in a loop of falling into elliptic singularity, sliding to hyperbolic singularity,escaping singularity and again reaching elliptic singularity. Therefore, a strategy that drives the SGCMG system to directly escape from the boundary of elliptic and hyperbolic singularity is proposed.

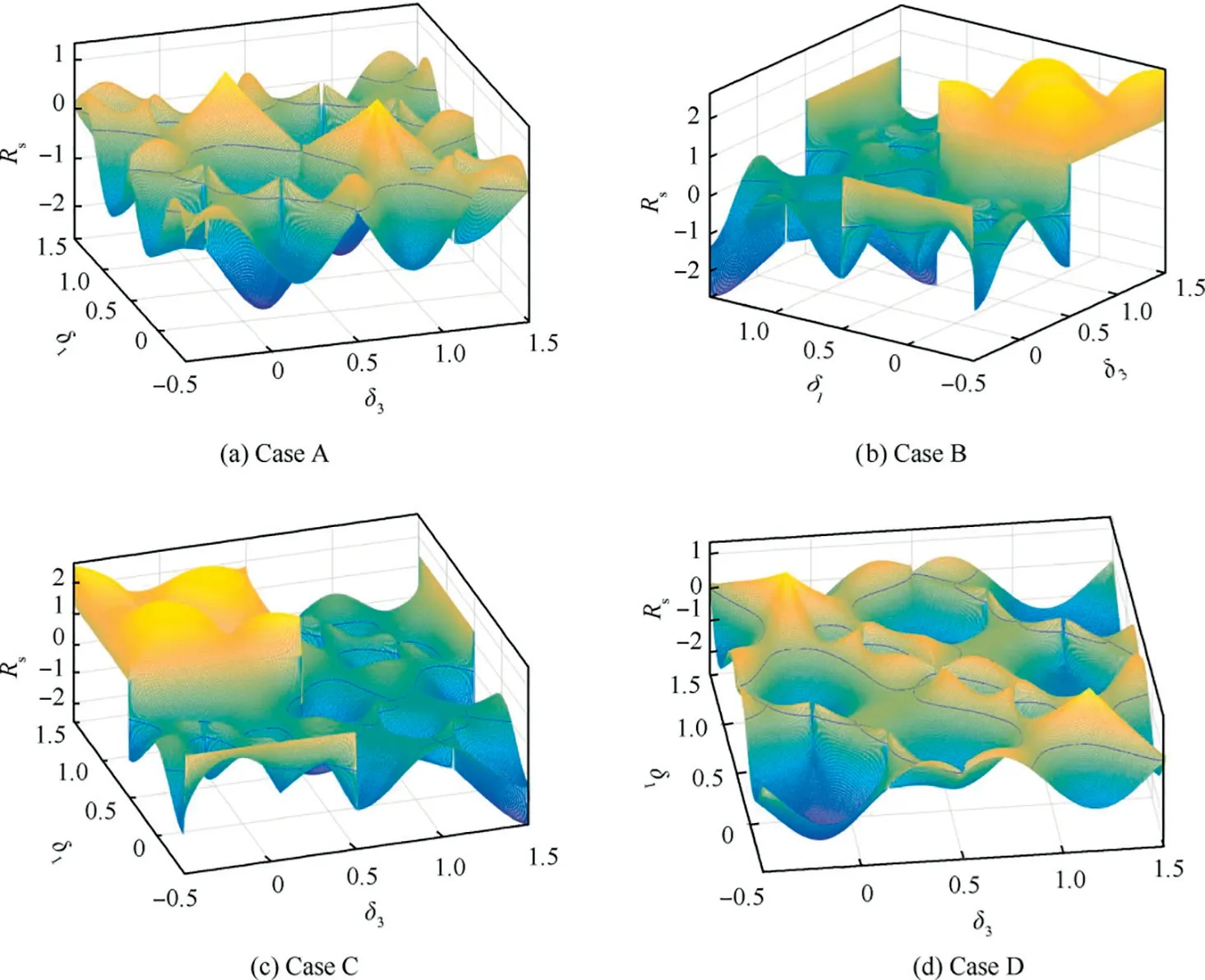
Fig. 1 Curved surface of Rs in singular states.

As demonstrated in Ref.8,one base vector of singular gimbal angle space degenerates to be a null vector of Jacobi matrix A in degenerate states which actually correspond to boundaries of different singularity types. Therefore, in the boundary, the total dimension of the space spanned by null space of matrix A and singular gimbal angle space is n-1,which is equivalent to）

Adopting singular value decomposition on E,the basic vector of the remaining dimension, denoted as ˙δb, could be acquired since it corresponds to the minimum singular value of E. It would generate additional torque and change gimbal angles since ˙δbdoes not belong to tangent space of singular surfaces and null space. Hence, it could be utilized to drive the system away from singularity. Through appropriately selecting sign of ˙δbto ensure that the additional torque caused by ˙δbwould increase rather than decrease angular velocity of spacecraft, ˙δBis set to satisfy

Then, to employ moderate degree of ˙δBin boundaries, the singularity radius gradient-based singularity-escape steering law is proposed as

where k1and k2are positive scalars to be properly selected.The exponential term is added to quickly increase the weight of vector ˙δBin steering law when the SGCMG system gradually approaches the boundary.

Remark 2. In the SRG steering law, the first item ˙δEwould quickly steer the SGCMG system to neighboring singular boundary, while the second item would drive the system to directly leave singularity from the boundary.

To make full use of SGCMG’s performance and escape singularity faster, the SRG steering law can be modified as

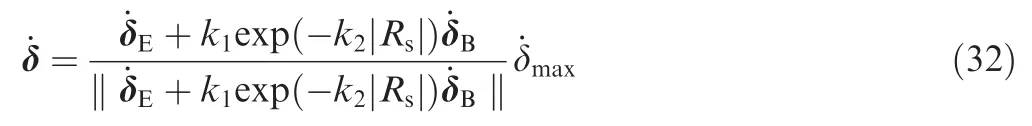
where ˙δmaxis the maximum gimbal angular velocity of the SGCMG system.

The above steering law only works when the system encounters an internal elliptic singularity.In nonsingular states and hyperbolic singularities,the system is steered by a singular direction avoidance steering law19with null motion,as follows:

where γ1=k3exp(-k4D), γ2=k5exp(-k6D), k3, k4, k5and k6are positive scalars to be appropriately selected, and u3is the vector that corresponds to minimum singular value of matrix A. When the SGCMG system falls into singularity, u3turns into singular direction u.

5. Simulation and analysis

This section first derives the expression of the proposed SRG steering law for pyramid-type configuration,and then presents the attitude control law and parameters used in the simulation.Finally, for comparison, three cases of simulations have been conducted to verify the effectiveness of the proposed steering law and its advantages over other steering laws.

5.1. SRG steering law for pyramid-type and skew-type system

where αi=72°(i-1), and β1represents the skew angle of the 5-SGCMG skew-type configuration.

The corresponding expression of SRG steering law can be acquired similarly following the above derivation of pyramid-type configuration and is omitted in consideration of length of article.

5.2. Spacecraft dynamics and control strategy

The attitude error dynamic model of rigid body spacecraft with SGCMGs is

where J is the inertia matrix; ωb, ωdand ωe=ωb-ωdare angular velocity, desired angular velocity and angular velocity error of spacecraft respectively; Tcdenotes the control torque.

where ωmaxis the maximum angular velocity and ˙ωmaxis the maximum angular velocity acceleration when spacecraft rotates around Euler axis; ΘEis the target value of rotation angle Θ.

The following PD-like controller26is employed for attitude maneuver control in simulations:

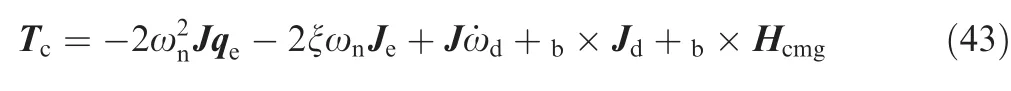
where ωnis the undamped frequency of oscillation,and ξ is the damping ratio.

The values of parameters of spacecraft dynamics and attitude control are given in Table 2. According to Eqs. (40)-(42), the values of t1, t2and t3can be calculated as t1=10 s,t2=20 s and t3=30 s.

To illustrate the benefits of the proposed steering law,three cases of simulations have been conducted. Moore-Penrose pseudoinverse steering law is applied before the SGCMG system runs into elliptic singularity to ensure that the same elliptic singular state is encountered in these cases.In Case 1 and Case 2,GSRI steering law20and the proposed SRG steering law are applied to manipulate a pyramid-type SGCMG system, while in Case 3,the proposed steering law is adopted to steer a skewtype configuration with five SGCMGs.

5.3. Simulation results of Case 1

As proposed in Ref. 20, the expression of GSRI is denoted as

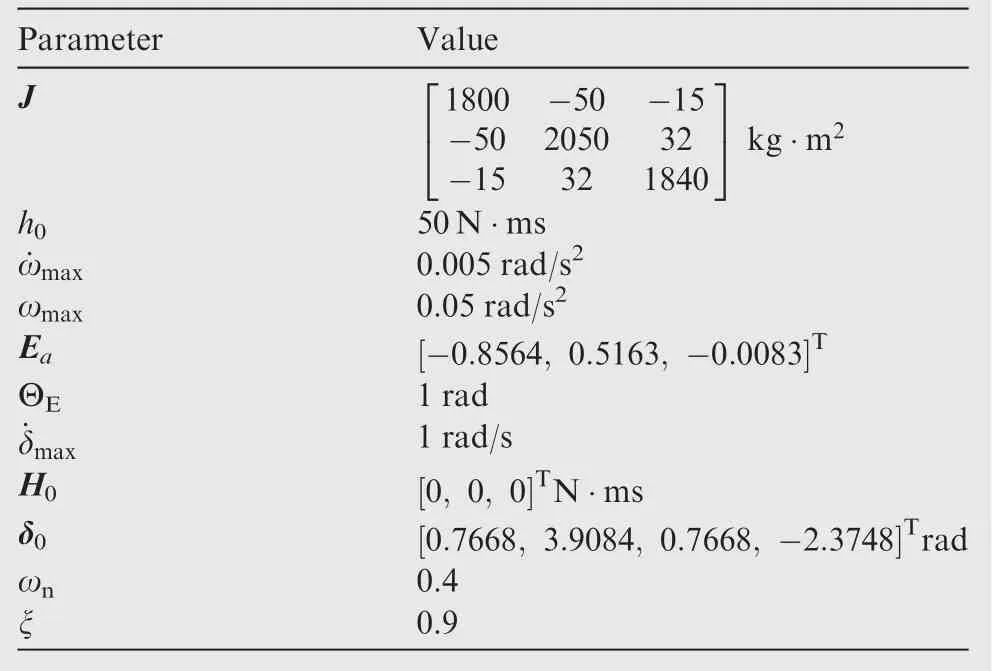
Table 2 Simulation parameters.

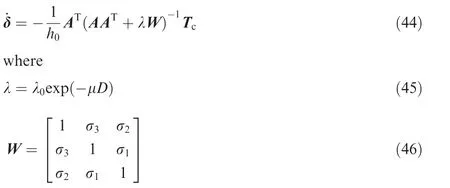
where σi=σ0sin(ω0t+ψi); λ0, μ, σ0, ω0and i are constant parameters to be chosen. The values of parameters of two cases are given in Table 3.

Simulation results of GSRI steering pyramid configuration are mainly shown in Figs. 3-6. Fig. 3 presents the attitude information including quaternion and angular velocity.Fig. 4 shows the detailed information about SGCMGs, suchas gimbal angles in Fig.4(a),gimbal angular velocity in Fig.4(b), output torque in Fig. 4(c) and torque error in Fig. 4(d).

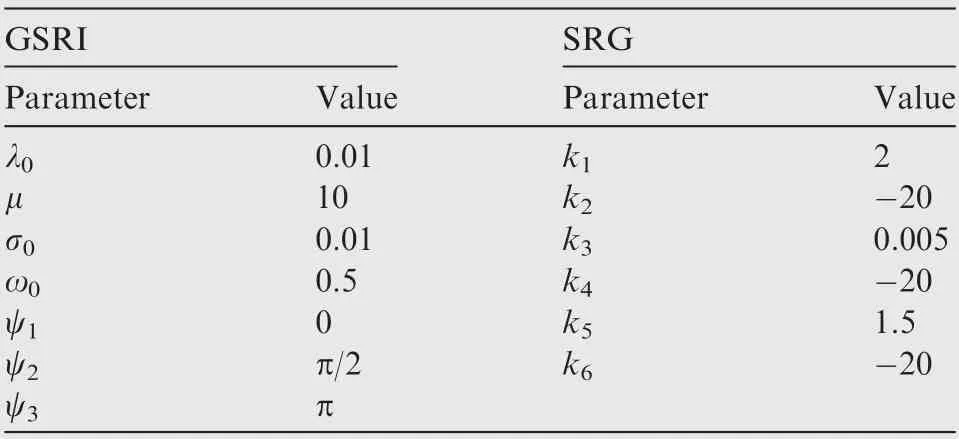
Table 3 Steering law parameters.

In Fig. 5(a), how the value of singularity radius changes when the system falls into elliptic singularity is illustrated,while in Fig. 5(b), the curve of singularity measurement D is presented. The GSRI steering law starts to work at 7.69 s which corresponds to Point A, and drives SGCMGs to reach Point E which is the boundary of elliptic and hyperbolic singularity at 10.18 s.Then at 10.41 s which corresponds to Point F,the value of D increases to 0.02.Note that singularity is considered to be escaped when D increases to 0.02 in the simulation.The value of singularity radius slowly increases at first and then goes down to zero during the phase when SGCMGs slide on elliptic surface.In Fig.6,the global graph shows part of 2H singular surface of pyramid-type configuration and the trajectory of Hcmg, while the partial graph distinctly shows the part of trajectory that the SGCMG system encounters and escapes from elliptic singularity.Fig.6 gives a clear view of how angular momentum of SGCMGs changes in angular momentum space. The phase when SGCMGs slide on elliptic singularity is highlighted by red line with arrows in Fig.6,and it is in fact hidden by the elliptic singular surface.

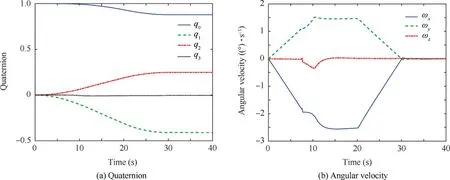
Fig. 3 Attitude information of Case 1.

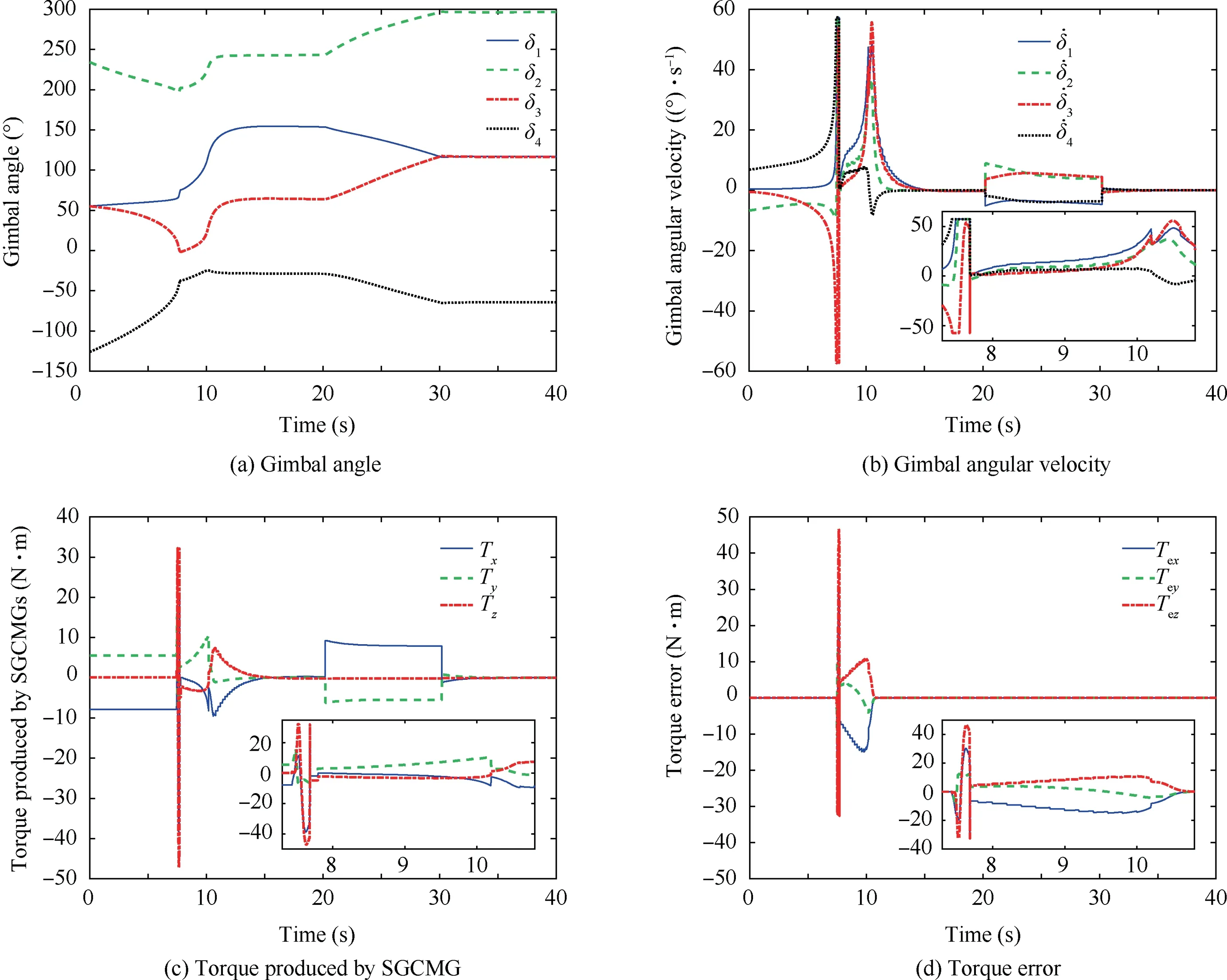
Fig. 4 SGCMG information of Case 1.

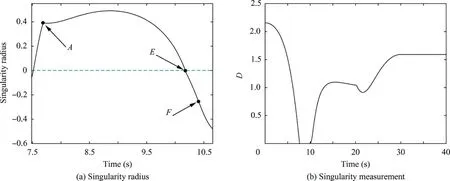
Fig. 5 Singular information of Case 1.

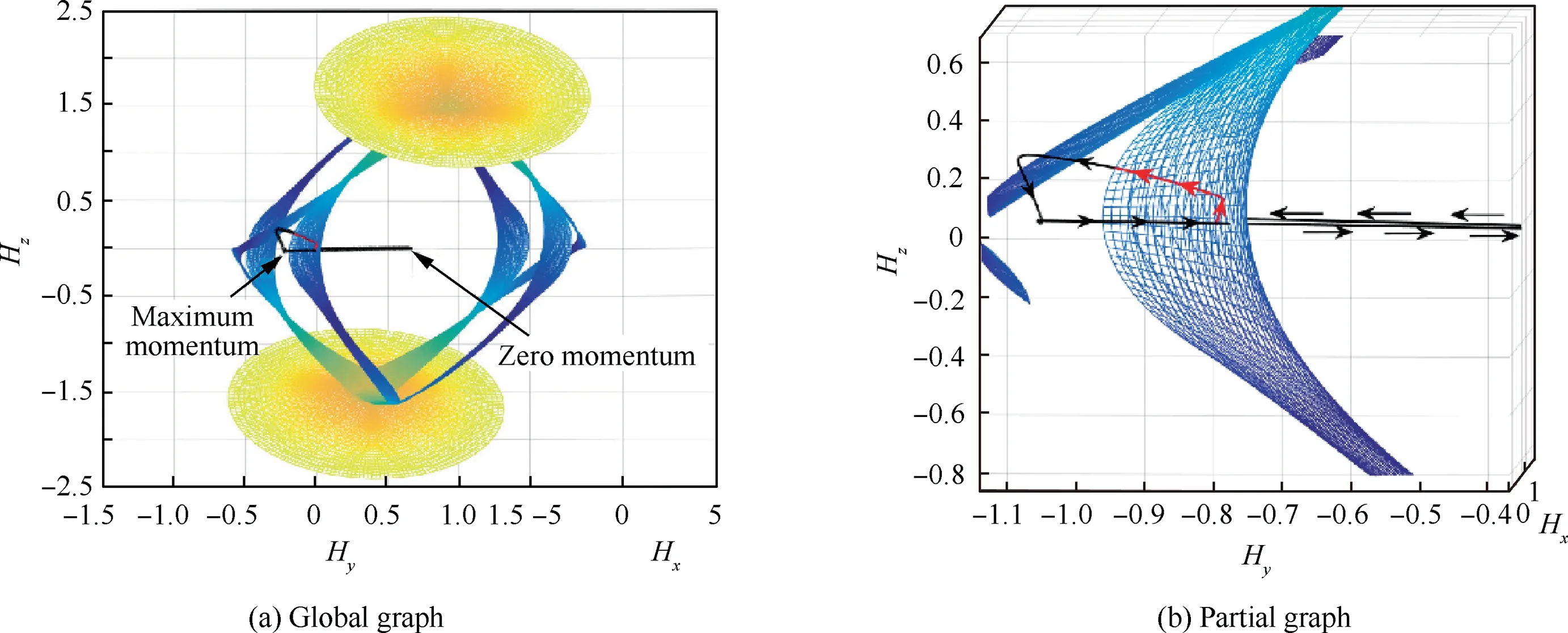
Fig. 6 Trajectory of Hcmg in Case 1.

As shown in Figs. 3-6, it is clear that GSRI steering law works well in nonsingular states since the SGCMGs realize torque command without error.But,in elliptic singular states,it takes 2.49 s to drive the SGCMG system to reach the singular boundary.

5.4. Simulation results of Case 2

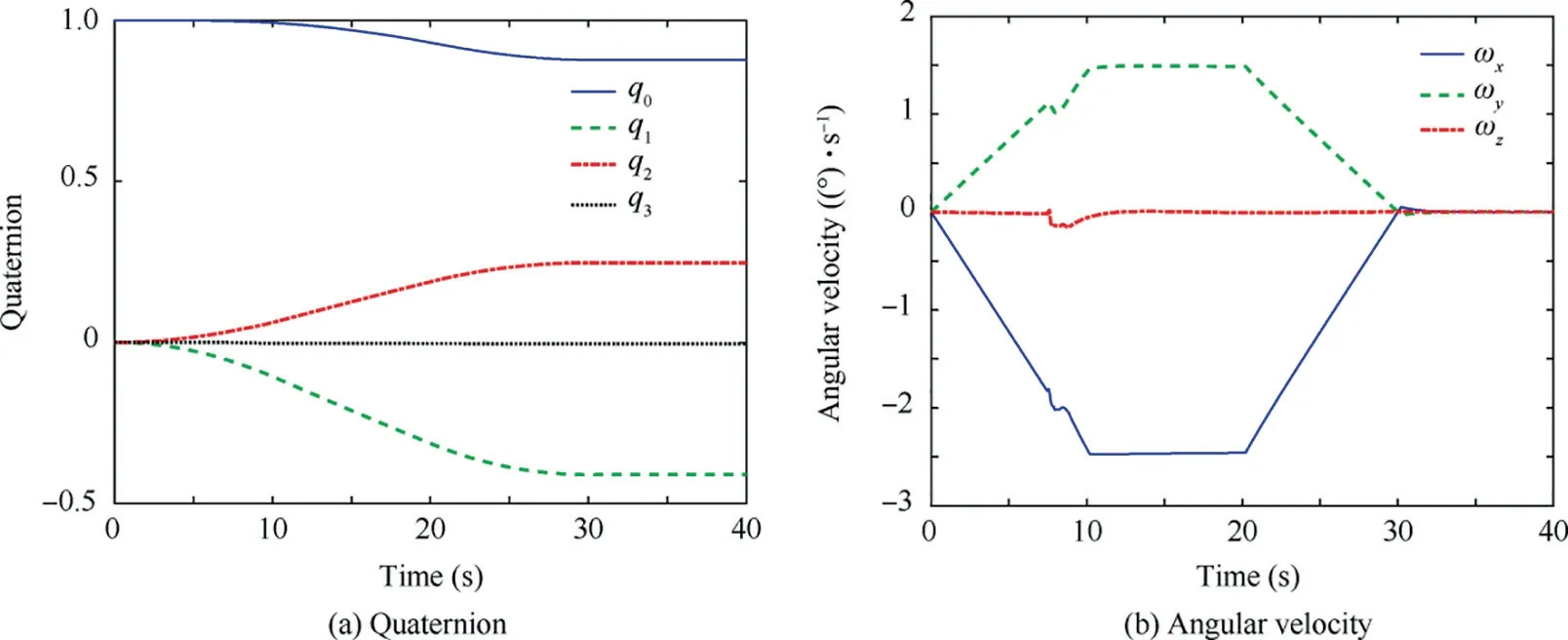
Fig. 7 Attitude information of Case 2.

The simulation results of SRG steering law manipulating pyramid configuration are shown in Figs.7-11.Figs.7-10 show the trajectories of the same variables as Case 1. As observed from Figs.7 and 8,the SRG steering law generates the same amplitude of maximum torque error in singular states as GSRI,but takes much shorter time to escape elliptic singularity.

In Fig. 9(a), it is observed that the SRG steering law starts to work at the same point A and the same time, and then rapidly leads the system to the boundary. When the value of singularity radius approaches to zero, the singularity-escape strategy comes into effect and arises an obvious turning Point B at 7.90 s. Then, the SGCMG system reaches Point C at 7.93 s in which the value of Rsequals zero. After that, the steering law switches to singular direction avoidance steering law with null motion in Eq.(33).At 8.39 s,the system reaches Point D where singularity measurement meets D=0.02 and singularity is escaped. Thus, only 0.24 s has been taken for SRG to realize escape from the elliptic singularity, which is approximately one-tenth that time of GSRI.

Comparing Figs. 5(b) with 9(b), we can see that the SGCMG system stays in singularity much shorter in Case 2 than in Case 1.Fig.10 similarly presents the trajectory of Hcmgin angular momentum space. It is explicitly shown that Hcmggoes nearly opposite direction to leave singularity, as compared to Fig. 6 in Case 1. In view of singularity radius,Fig. 11 presents how the two steering laws drive the system to move on singularities. Fig. 11(a) shows the trajectory of Rsof two cases when the SGCMG system stays in singularity and the curved surface corresponds to Case B shown in Fig.1(b),while Fig.11(b)shows the details with enlarged scale.The red line represents the trajectory of GSRI and the black line indicates the trajectory of SRG.The important points of steering process marked in Figs.5(a)and 9(a)are similarly marked in Fig.11b.In the trajectory of GSRI,due to the fact that the value of Rsis slightly smaller than that of singular surface,the beginning part shown by red dashed line is covered by the curved surface. The starting Point A is actually in hillside of the local curved surface,and Rsgoes straightly down the slope under the guide of SRG in Case 2, while the trajectory of GSRI in Case 1 climbs to the top and goes downhill in another side,which makes the system take more time to escape elliptic singularity.

5.5. Simulation results of Case 3

Since the chosen internal 3H elliptic singularity in this case has larger angular momentum than that in Cases 1 and 2,the maximum angular velocity of spacecraft will accordingly become larger. Thus, as shown in Table 4,the value of several simulation parameters are properly modified and other parameters remain the same as in Tables 2 and 3. Similar to the above two cases, the simulation results of five-SGCMG skew-type system are shown in Figs. 12-14. As observed from Figs. 12 and 13, the SRG steering law can steer the skew-type configuration away from singularity in quite a short time.

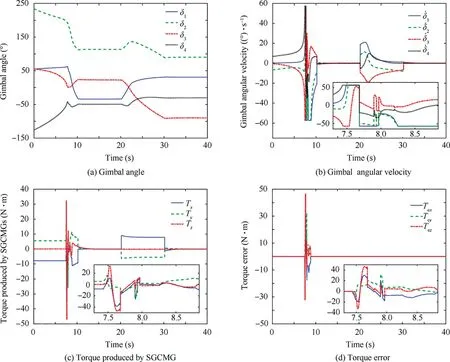
Fig. 8 SGCMG information of Case 2.

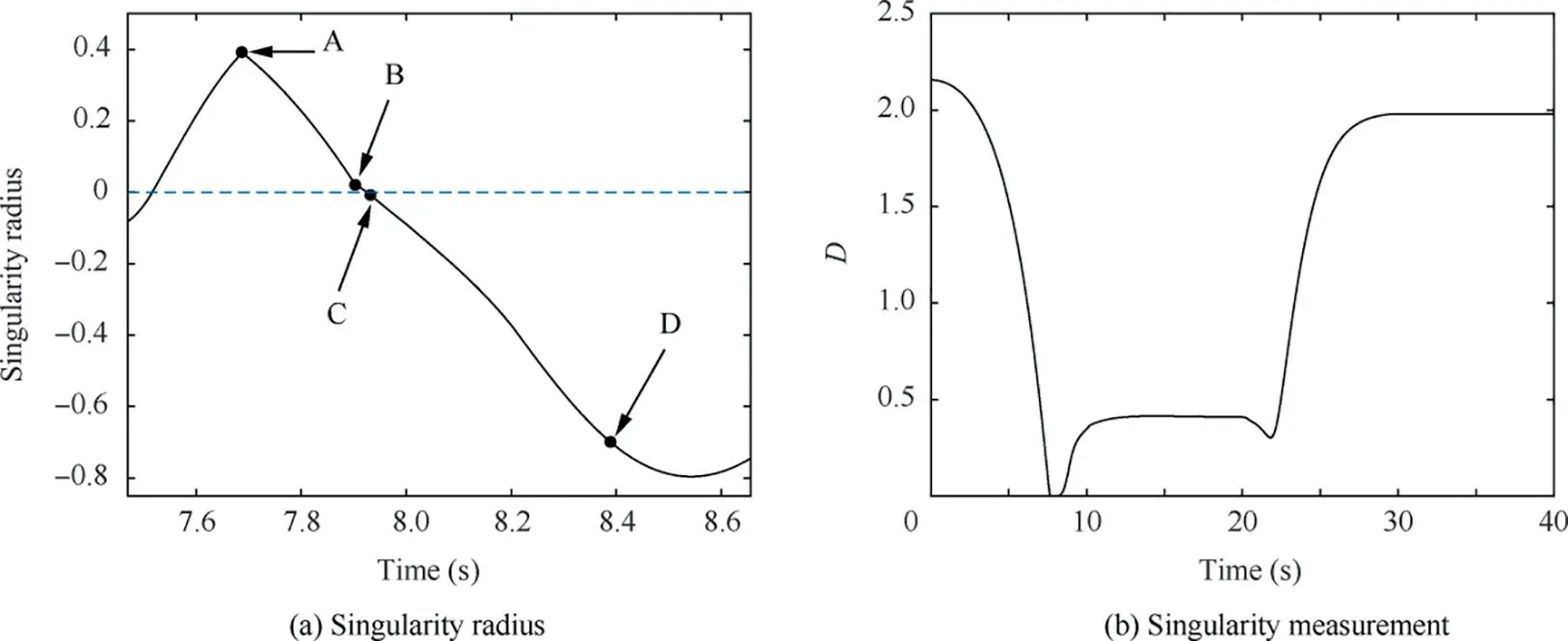
Fig. 9 Singular information of Case 2.

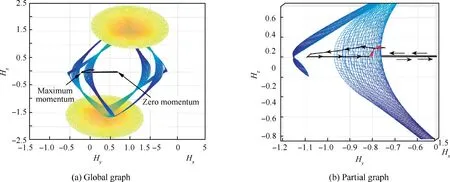
Fig. 10 Trajectory of Hcmg in Case 2.

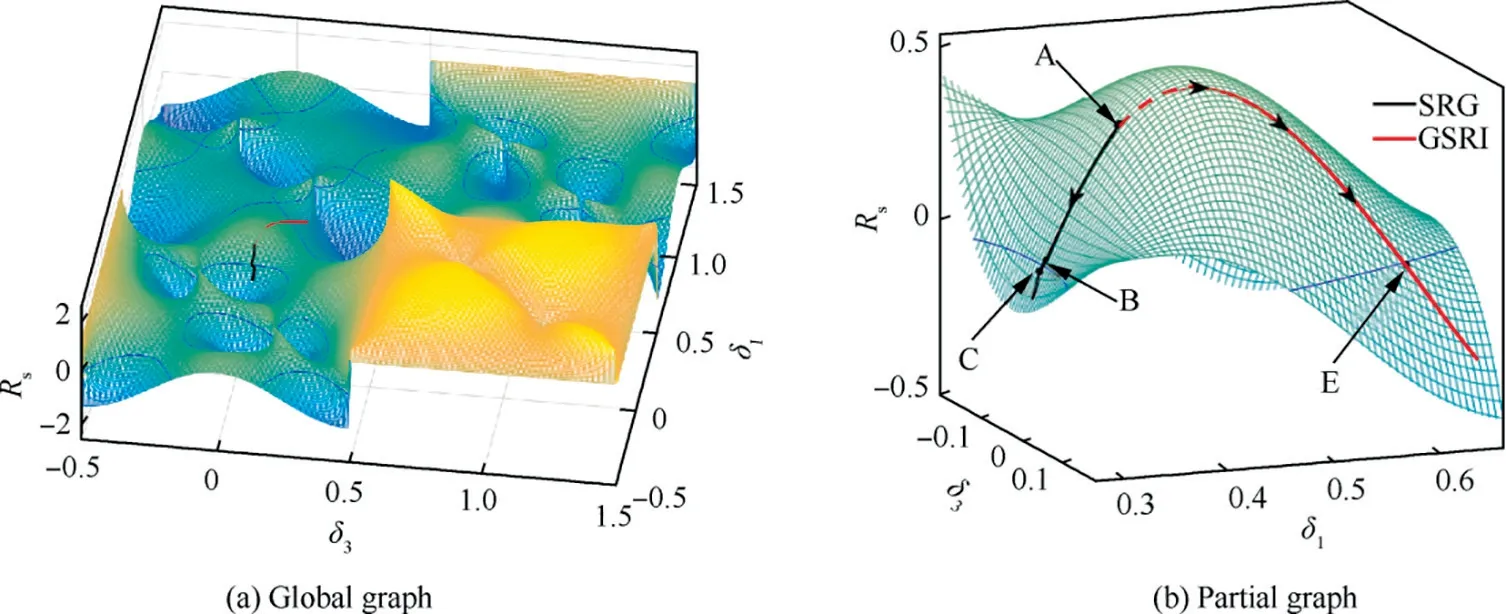
Fig. 11 Trajectory of Rs in Cases 1 and 2.

In Fig. 14(a), the steering process of SRG steering law which is similar to that in Case 2 is clearly shown. The proposed steering law starts to manipulate the system at 8.60 s which corresponds to Point G,and leads the system to slide on elliptic singularity. As the system approaches singular boundary, the singularity-escape strategy comes into effect at Point H. Then, the SGCMG system reaches Point L whose value almost equals zero at 8.74 s and the steering law switches to singular direction avoidance steering law.At 8.90 s which corresponds to point M, the value of D increases to 0.02 and the system is considered as realizing escape from singularity.Thus,the SRG steering law only takes 0.14 s to drive the skew-type system out of elliptic singularity and it is valid for all SGCMG systems.

Besides, to clarify the advantage of SRG steering law, simulations of the revised singular direction avoidance steering law expressed in Eq. (33) and the rapid singularity-escapesteering law developed in Ref. 25, which are abbreviated as rSDA and RSE respectively, have been conducted. The SGCMG system is chosen as pyramid configuration and simulation results are given in Table 5, where Tsrepresents the time duration of the system sliding on elliptic singularity,‖Φe‖mdescribes the maximum amplitude of error Euler angles Φeduring maneuver. As shown in Table 5, rSDA and GSRI have approximately the same performance index during steering the SGCMGs, and the other two rapid singularityescape steering laws take much shorter time to escape elliptic singularity during which RSE and SRG generate smaller attitude errors. Compared to RSE, the SRG steering law escapes the elliptic singularity slightly faster, and it requires no extra storage data of singular boundaries.

Table 4 Simulation parameters of Case 3.

Fig. 12 Attitude information of Case 3.

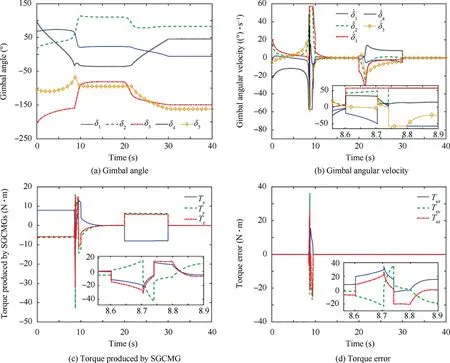
Fig. 13 SGCMG information of Case 3.

Fig. 14 Singular information of Case 3.

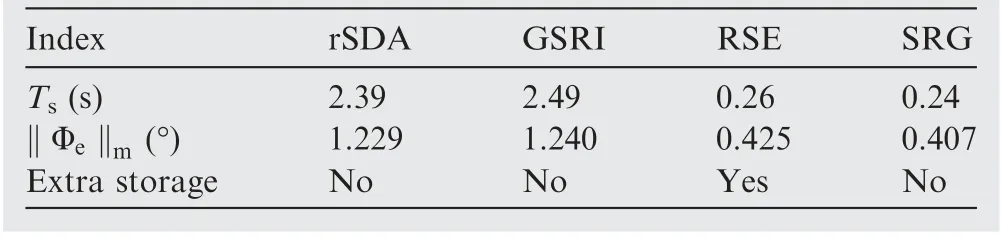
Table 5 Simulation results of four typical steering laws

6. Conclusions

This paper proposes a novel singularity description parametersingularity radius based on Gaussian curvature to describe singular degree of singularities.Then,the physical meaning of singularity radius is discussed on the basis of its geometric expression, and it is applied to distinguish singularity type.The singular states of pyramid-type configuration are visualized clearly by using singularity radius and singularity analysis method. Afterwards, an analytical singularity radius gradientbased steering law is proposed to solve the elliptic singularity escape problem.The residual base vector of degenerated singular states is utilized to drive the SGCMG system to leave singularity in boundary. The advantages of SRG are that it can realize a rapid singularity escape,and it requires no knowledge of other singularities and little computation since SRG is a local steering law with analytical expression. In addition, simulations of bang-off-bang maneuver on pyramid-type and skew-type configuration illustrate the effectiveness of SRG steering law and that it is able to find a closer way than GSRI to escape elliptic singularity.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

This study was funded under the National Natural Science Foundation of China (No. 61873312).