A user-friendly yield criterion for metals exhibiting tension-compression asymmetry

Lei CHEN, Weidong WEN, Hongjian ZHANG

a Faculty of Civil Engineering & Mechanics, Jiangsu University, Zhenjiang 212013, China

b College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

KEYWORDS Ni3Al based alloy;Plastic anisotropy;Plastic deformation;Tension-compression asymmetry;Yield criterion;Yield stress

Abstract The aim of this paper is to model the yielding asymmetry of pressure-insensitive metals,including but not limited to Ni3Al alloys. The main focuses are put on the flexibility and manipulative convenience. The parameters of theory are kept to a minimum and can be determined by as few tests as possible.These requirements are fulfilled by constructing a yield function using the second and third-invariants of a linearly transformed stress tensor.The proposed yield criterion has a simple mathematical form and has only seven parameters when used in three-dimensional stresses.Compared with existing theories,the new yield criterion has much fewer parameters,which makes it very convenient for practical applications.The coefficients of the criterion are identified by an error minimization procedure. Applications to a Ni3Al based intermetallic alloy as well as a Cu-Al-Be shape memory alloy and comparison to other criteria show that the proposed criterion has nearly the same predictive ability and flexibility with other criteria. The proposed yield criterion can estimate the coefficients by using less data, which is a big advantage compared with other similar theories, especially when there is a limited number of experimental data.

1. Introduction

Due to the positive temperature dependence of the flow stress in a finite temperature domain, known as a ‘‘stress anomaly”,Ni3Al exhibits excellent high temperature properties. In general, Ni3Al has good tensile and compressive yield stresses in the temperatures range 650-1100°C. Besides, Ni3Al has the good properties of superior creep and fatigue resistance, superior oxidation and hot corrosion resistance.1,2Ni3Al is one of the most extensively studied intermetallic compounds from both fundamental and practical points of view. After more than half a century of research, Ni3Al-based alloys are expected to be excellent materials in aeronautics and astronautics fields.3

However, the application of Ni3Al alloys in the aviation industry is limited presently due to the lack of knowledge about their complex mechanical behaviors, and the inherent conservatism of the aerospace industry.Few studies have been done on the cost-effective manufacturing of cast and wrought Ni3Al alloys. It is generally known that the plastic analysis of metal forming processes depends on the yield criterion and associated plastic flow rules employed. In order to improve the accuracy of numerical plastic forming simulations, it is essential to develop appropriate yield criteria involved.4Given their importance to plastic forming analysis, tremendous yield criteria have been proposed for both isotropic materials5-9and anisotropic materials.10-16For reviews concerning yield criteria of metals one may refer to Refs. 17,18. And for latest research concerning yielding behavior of metals,one may refer to Refs. 19-24.

For Ll2-long-range ordered intermetallic alloys, such as Ni3Al, remarkable Strength Differential (SD) effects are observed for their violation of Schmid’s law25. To model the strength differential effects of pressure insensitive metals,yield criteria that can describe SD effects of metals have been proposed in recent years.26-29Those criteria have gained a lot of attention and some have been used to describe the SD effects of engineering materials.30-34

Compared to the tremendous anisotropic yield functions proposed for materials with equal tension and compression,criteria that can model both plastic anisotropy and yielding asymmetry are still lacking.In order to model the complicated plastic behaviors of metals with SD effects, additional parameters are needed. However, over many parameters need more experiment data to calibrate the theory, which has resulted in difficulties in practical applications. For example, in order to calibrate Cazacu and Barlat’s 2004 criterion,26beside experimental yield stresses, experimental Lankford coefficients (rvalues)along different orientations are also needed.Sometimes accurate r-values of metals are difficult to obtain.For example,due to the plastic localization bands in specimen when subjected to uniaxial tension, the r-values of a directionally solidified Ni3Al based alloy are difficult to precisely evaluated (see Fig.1).Thus,yield functions with fewer parameters are highly necessary to model the plastic behaviors of those materials.In the next section, a new anisotropic yield criterion with fewer parameters that can model the SD effects of pressure insensitive metals, including but not limited to Ni3Al alloys, will be suggested.

2. A new orthotropic yield criterion

2.1.Development of an orthotropic yield criterion for describing the asymmetry in yielding of metals

In the following we will propose an orthotropic yield criterion that can describe both plastic anisotropy and yield asymmetry of pressure insensitive metals.There are several ways available to extend an isotropic criterion to anisotropy,such as the‘‘Isotropy Plasticity Equivalent’’ (IPE) method introduced by Karafillis and Boyce35and the methodology based on the use of linearly transformed stress tensors.15

For the linear transformation methodology, the transformed stress tensor ～S is defined as36:

where C is a fourth-order anisotropic tensor charactering the anisotropy of materials,while K is the fourth-order symmetric deviatoric unit tensor by which the Cauchy stress tensor σ is transformed to its deviator s, and L=CK is a fourth-order symmetric tensor. Specially, in any Cartesian coordinate system:

Fig. 1 Plastic localization bands in specimens cutting from different directions θ with respect to solidification direction of Ni3Al based alloy IC10 when subjected to uniaxial tension.

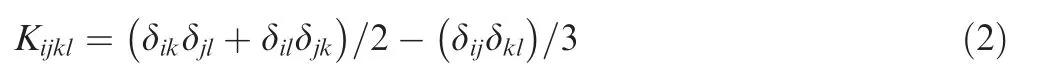
where δijrepresents the Kronecker delta and i,j,k,l=1,2,3.

By using the second and third invariants of the transformed stress tensor ～S, one can extend any isotropic yield criterion presented by the traditional stress invariants J2and J3to orthotropy.If x,y,and z coincide with the three principal axes of anisotropy and if the stress tensor is represented by the 6-dimensional vector σ=[σxxσyyσzzτyzτzxτxy],the symmetric tensor L can be expressed by the 6×6 matrix37:

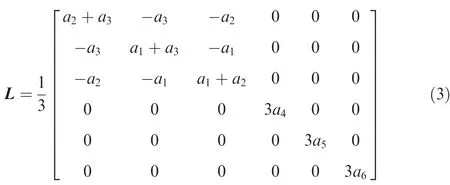
where a1, a2, a3, a4, a5, a6are independent parameters charactering the anisotropy of materials. For isotropic condition, all the coefficients ak(k=1,2,...,6)are equal to unity, ～S reduces to the stress tensor deviator s.The second and third invariants of the transformed stress tensor ～S, denoted by ～J2and ～J3, can be expressed in terms of the components of the Cauchy stress as37:

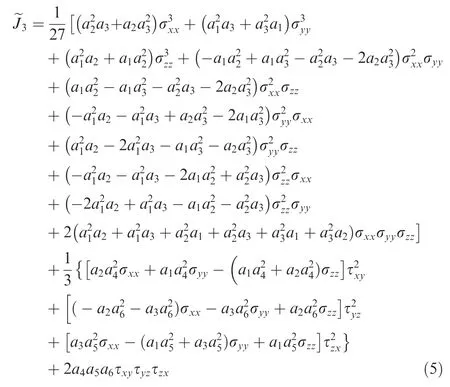
when all the coefficients are equal to unity, ～J2and ～J3reduce to the isotropic invariants J2and J3. A lot of yield functions in literature can be expressed in terms of the second and third invariants of the transformed tensor ～S. For example, the Yld91 yield function14for Body Centered Cubic(BCC)metals and Face Centered Cubic (FCC) metals, expressed as Yld91BCCand Yld91FCCcan be expressed in terms of ～J2and～J3as36:

which implies that ～J2and ～J3are insensitive to hydrostatic pressure. Also ～J2and ～J3are invariants to any transformation belonging to the symmetry group of the material. If all the coefficients ak(k=1,2, ... ,6) are set to unity, ～J2reduces to J2and ～J3reduces to J3.

Obviously, the proposed orthotropic criterion is insensitive to hydrostatic pressure,which is consistent with the hypothesis that hydrostatic pressure does not cause plastic deformation of metals.

For a thin sheet perpendicular to the z axis and in a condition of plane stress (σxx, σyy, τxy)

where σ1, σ2are principal stresses. As mentioned earlier,manipulative convenience and keeping parameters of theory to a minimum are the main focuses of this paper. Table 1 shows the number of parameters for different yield criteria which can describe the SD effects of metals, namely, Cazacu and Barlat(2004)26,Chen et al.(2013)39and the proposed criterion.Obviously,the proposed criterion has much less parameters compared to other similar existing yield criteria in literature.

Suppose a uniaxial tension σθdirected at an angle θ with the x axis then

If σTθand σCθare the yield stresses of the tensile and compressive testing specimens under uniaxial loading.Substituting(17)-(15), it follows that

In condition of equibiaxial tension, yielding occurs when σ11=σ22=σTb, thus

Table 1 Number of parameters for different yield criteria.

Further,let rθbe Lankford coefficients,namely,the ratio of transverse to through thickness increment of the logarithmic strain in condition of uniaxial loading directed at angle θ with x axis, then

Substituting θ=0°, 45°, 90° in both tension and compression conditions to the above equation, we can get additional six equations containing the coefficients of the yield criterion.

2.2. Numerical calculation of the anisotropy parameters

For a state of plane stress, the proposed yield criterion (Eq.(15))contains 5 adjustable parameters a1,a2,a3,a4and α.Particularly, when τxy=0, the proposed criterion (Eq. (16)) have only 4 adjustable parameters(a1,a2,a3and α).In order to calibrate the anisotropy parameters in condition of plane stress,the following experimental data could be adopted: σT0, σC0,σT45, σC45, σT90, σC90, σTb, σCb, rT0, rC0, rT45, rC45rT90, rC90. The choice of the reference yield stress is arbitrary. As a result, we may get the following set of 14 equations:

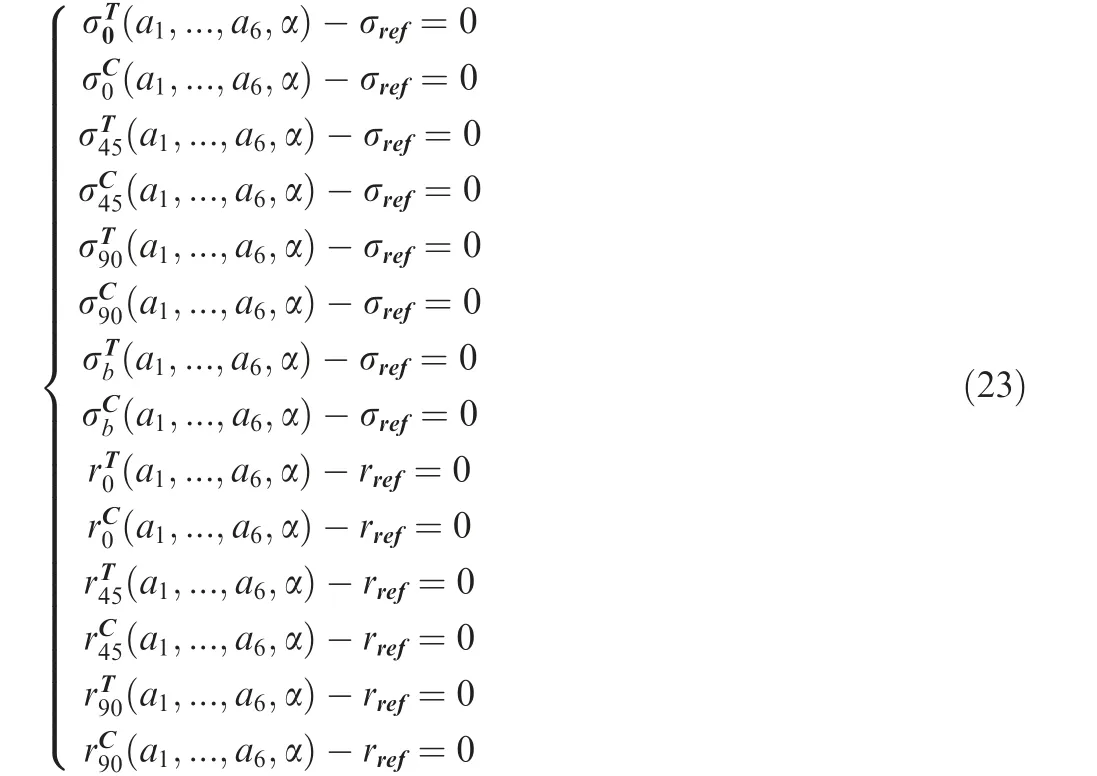
Here, ‘‘n” and ‘‘m” represent the number of yield stresses and r-values, respectively for different orientations θ, the superscript indicates whether the respective value is experimental data or calculated theoretical results according to the proposed criterion while λi, ηi, μ and γ are weight factors.

The next work is to optimize the anisotropy parameters a1,a2...,a6and α,respectively,so as to get a minimum of the error function. There are different mathematical methods to solve such a problem. The method of steepest descent is one of the most convenient methods, which will be adopted in this paper.40

It is believed that the error minimization procedure discussed above is a great engineering method to examine a yield criterion’s flexibility:a yield function is flexible enough for general purpose only if it can ‘‘pass” the error minimization procedure test.41In the following the new yield function will be applied to different materials to illustrate its predictive capability.

3. Applications

In order to check the proposed yield criterion’s predictive ability and flexibility, in the following we will apply it to two different metallic materials:a Ni3Al based intermetallic alloy and a shape memory alloy Cu-Al-Be. An important reason for choosing those materials is that their yield loci exhibit widely different shapes, which is preferred to check a yield function’s flexibility.

3.1. Testing material Ni3Al based intermetallic alloy IC10

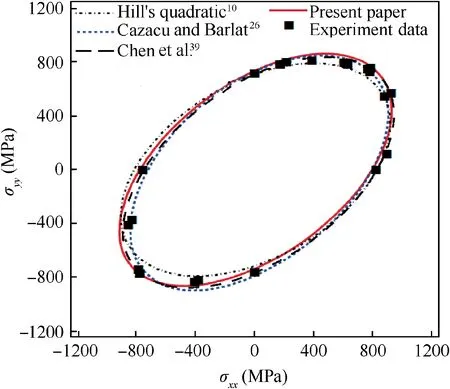
Fig. 2 Yield loci of Ni3Al based alloy IC10 predicted by Hill’s quadratic criterion, Cazacu and Barlat26, Chen et al.39 and proposed criterion.

Table 2 Experimental material data of Ni3Al based alloy IC10.

Table 3 Calculated parameters in different yield functions for Ni3Al alloy IC10.

Table 4 Calculated parameters of Hill’s quadratic yield function for IC10.

Table 5 Experimental material data of shape memory alloy Cu-Al-Be.45

Next, we consider the experimental series of the Ni3Al based super-alloy IC10, which was developed as blade materials in advanced aero-engines.42Due to the preferred<0 0 1 ＞crystallographic orientation and tension-compression asymmetry of the Ll2-long-range ordered Ni3Al,25the directionally solidified alloy exhibits both plastic anisotropy and yielding asymmetry between tension and compression. The authors of the present paper43,44have studied the plastic behavior of alloy IC10, the yield locus according to 0.2% plastic strain of the largest principal strain was obtained by biaxial tensile tests on cruciform specimens and bi-compression tests on cubes.The experimental material data for alloy IC10 is given in Table 2.and Barlat (2004) and Chen et al. (2013), additional experiment data of r-values are needed. As the accurate r-values are not available, rT0, rC0, rT90and rC90are assumed all equal to one and used as additional input data. In order to reduce the errors brought by the assumption of r-values, the weight factors of the r-values (i.e., ηi) are set much smaller than other weight factors when performing the error minimization procedure. The calculated parameters for yield functions of Cazacu and Barlat(2004)and Chen et al.(2013)are given in Table 3.It can be seen that the yield loci of Cazacu and Barlat (2004),Chen et al. (2013) and the proposed yield criterion are very close and all can describe the asymmetric yield behavior of alloy IC10 well. The results illustrate that the proposed yield function, with much fewer parameters, has nearly the same predictive ability and flexibility as Cazacu and Barlat (2004)and Chen et al. (2013).

3.2. Testing material Cu-Al-Be shape memory alloy

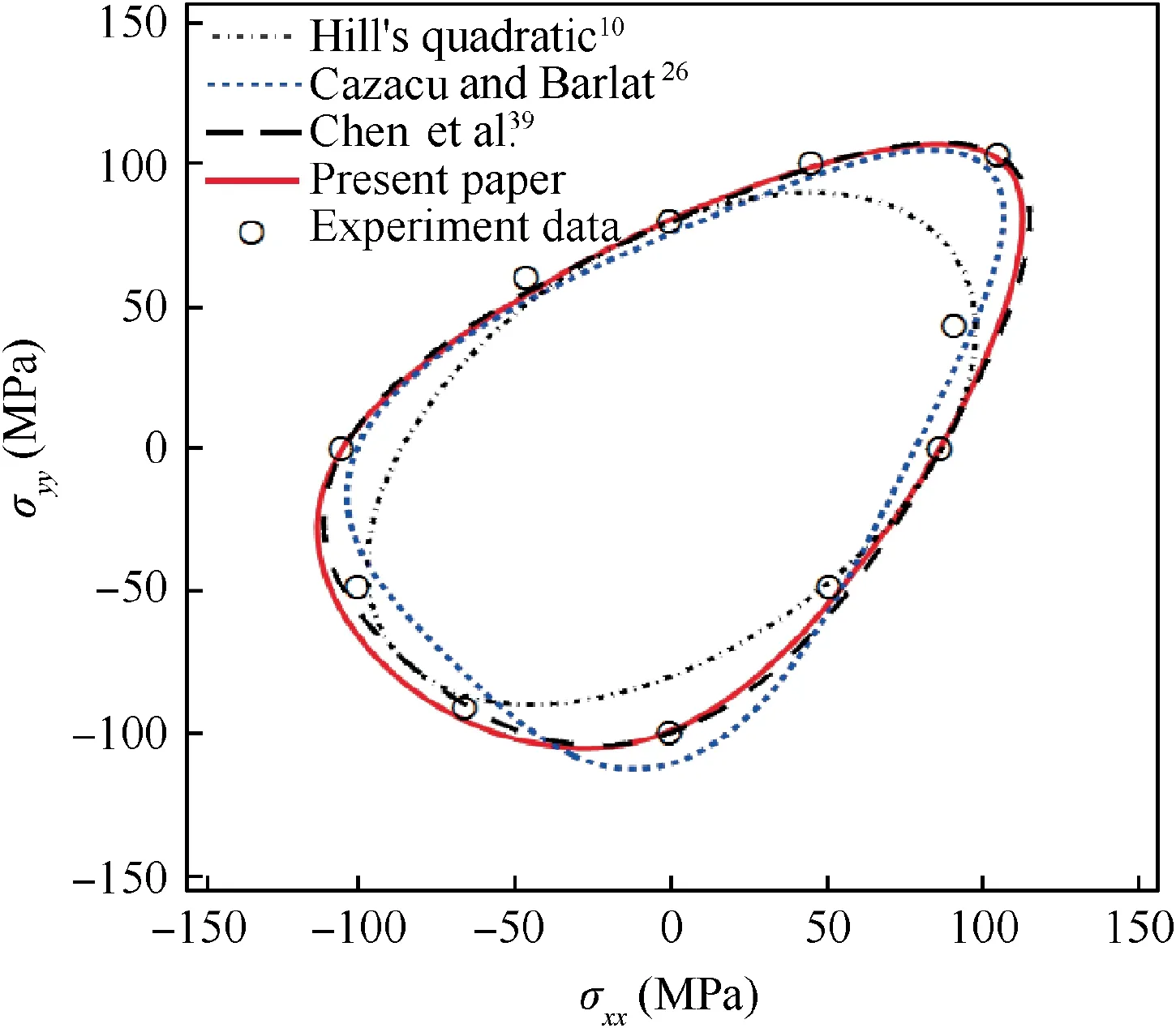
Fig.3 Yield loci of Cu-Al-Be SMA predicted by Hill’s quadratic criterion, Cazacu and Barlat26, Chen et al.39 and proposed criterion (experiment data after Bouvet45).

For the sake of comparison,yield loci predicted by Cazacu and Barlat (2004)26and Chen et al. (2013)39, which can describe the SD effects of metals, are also presented in Fig. 2. In order to calibrate the yield functions of Cazacu Shape Memory Alloy (SMA) often exhibits an asymmetric behavior between tension and compression. Bouvet et al.45have conducted experimental studies on the anisotropy of a Cu-Al-Be SMA. The initial yield locus was obtained by bicompression tests on cubes and tension (compression)-internal pressure on tubes. The experimental material data for Cu-Al-Be is given in Table 5.Fig.3 shows the experimental yield locus of Cu-Al-Be SMA corresponding to 0.2% plastic strain of the largest principal strain(experiment data is plotted by symbols).Note that the yield locus of Cu-Al-Be SMA has a significant asymmetrical shape, the yield stress in compression is 20% larger than in tension.

Fig.3 also shows the theoretical yield locus of the proposed criterion given by Eq.(16).The experiment data σT0,σC0,σT90,σC90andare selected as input data to calibrate the yield criterion. The parameters for the proposed criterion, calculated using the error minimization procedure described in Section 2.2, are listed in Table 6.

The theoretical predictions fit the experimental data well,the proposed criterion can describe well the anisotropy and SD effects in yielding of Cu-Al-Be SMA. The yield locus of Hill’s quadratic criterion10is also potted in Fig.3 for comparison. The calculated parameters for Hill’s quadratic criterion are given in Table 7. For Hill’s quadratic criterion, significantdiscrepancies are found for some stress states, especially for equi-biaxial tension and uniaxial compression states.It should be mentioned that tensile yield stresses are used here to calibrate the parameters of Hill’s theory, therefore the theoretical uniaxial compressive yield stresses do not coincide with experiment data. As Hill’s quadratic criterion is based on the hypothesis of tension-compression symmetry, therefore failed to reproduce the asymmetry shape of the experimental yield locus of alloy Cu-Al-Be. From Fig. 3 we can also see that,modeling the plastic behavior of metals with remarkable tension-compression asymmetry by symmetric yield functions will cause significant errors.

Table 6 Calculated parameters in different yield functions for shape memory alloy Cu-Al-Be.

Table 7 Calculated parameters of Hill’s quadratic yield function for Cu-Al-Be.

In order to compare the predictive ability of the proposed theory with existing asymmetric yield criteria, the theoretical yield loci of Cazacu and Barlat (2004)26as well as Chen et al. (2013)39are also plotted in Fig. 3. In order to calibrate the yield criteria of Cazacu and Barlat (2004) and Chen et al. (2013), additional experiment data such as r-values are needed. As the r-values are not available, rT0, rC0, rT90and rC90are assumed all equal to one and used as additional input data.In order to reduce the errors brought by the assumption of rvalues,the weight factors of the r-values ηiare set much smaller than other weight factors when performing the error minimization procedure. The calculated parameters for yield functions of Cazacu and Barlat (2004) and Chen et al. (2013)are given in Table 6. In general, the yield loci of Chen et al.(2013) and the proposed yield criterion are very close and all can describe the asymmetric yield behavior of Cu-Al-Be SMA well. However, the predicted yield locus of Cazacu and Barlat (2004) departures from the other two yield functions in some regions,especially near equibiaxial compression region and uniaxial transverse compression region. Compared to other asymmetric yield criteria, Cazacu and Barlat (2004) criterion undervalues the yield stresses near equi-biaxial compression region and overvalues the transverse compressive yield stress a little bit. That may be caused by the input data of the hypothetical r-values, rather than experimental values. If the hypothetical r-values are closer to the real ones, we may get better predictions. It should be noted that the proposed yield function overvalues the yield stresses near the equibiaxial compression state slightly. Overall, the proposed yield function has nearly the same predictive ability and flexibility as existing theories, but with much fewer parameters.

4. Conclusions

The aim of this paper is to model the yielding asymmetry of pressure-insensitive metals, mainly for but not limited to Ni3-Al alloys. The yield criterion proposed in this paper is phenomenological, so the application range and limitations of the model should be checked by experiments. If the proposed yield criterion is adaptive to other materials except for Ni3Al and Cu-Al-Be shape memory alloys is still need further research. For now, we can reach the following conclusions:

(1) Experimental results show that the anisotropic yield criterion proposed in this paper can describe well both plastic anisotropy and yielding asymmetry of Ni3Al based intermetallic alloys as well as Cu-Al-Be shape memory alloys.

(2) Comparison with existing theories illustrates that the proposed yield criterion has nearly the same predictive ability and flexibility like other similar criteria in literature, but with much fewer parameters.

(3) The proposed yield criterion can estimate the coefficients by using less data, which is a big advantage compared with other similar theories, especially when there is a limited number of experimental data.

Acknowledgements

The authors are grateful for the financial support for this work by Natural Science Foundation of Jiangsu Province, China(No.BK20160486)and the National Natural Science Foundation of China (No. 91860111).