A novel surrogate modeling strategy of the mechanical properties of 3D braided composites

Zeyi LIU, Yuliang HOU, Qiaoli ZHAO, Cheng LI

KEYWORDS Braided composites;Diffuse approximation;Elastic properties;Multiscale model;Surrogate model

Abstract In this paper, a surrogate-based modeling methodology is developed and presented to predict the elastic properties of three dimensional (3D) four-directional braided composites. Using this approach, the prediction process becomes feasible with only a limited number of training points. The surrogate models constructed using Finite Element (FE) method and Diffuse Approximation, reduce the computational time and cost for preparing experimental samples. In the FE model, multiscale method is applied to couple the computations of elastic properties at microscale and mesoscale. Subsequently, a parametric study is performed to analyze the effects of the three design parameters on the elastic properties. Satisfactory results are obtained via the surrogatebased modeling predictions, which are compared with the experimental measurements. Moreover,the predictions obtained from surrogate models concur well with the FE predictions.This study orients a new direction for predicting the mechanical properties based on surrogate models which can effectively reduce the sample preparation cost and computational efforts.

1. Introduction

Three dimensional braided composites have been widely used as structural components in aviation, aerospace and other types of advanced structures due to their excellent mechanical performances, such as high transverse strength, high shear stiffness and high damage tolerance.1-5As an anisotropic material, investigations on the mechanical properties of 3D braided composites have caught the attention of scholars over the last few decades. However, the experimental procedures are quite complex and expensive to characterize the mechanical stiffness and the effects of technical parameters on the mechanical properties of 3D braided composites, such as braiding angle, fiber volume fraction etc. Therefore, a reliable prediction method needs to be developed to accurately evaluate the mechanical properties of 3D four-directional braided composites, while pursuing lower specimen preparation expense and computational cost.

Numerous theoretical methods have been developed to estimate the mechanical constants of 3D four-directional composites6-8based on the homogenization method proposed by Oleinik et al.9These theoretical methods provide us convenient tools to predict the mechanical behaviors of 3D fourdirectional braided composites under various loading scenarios. However, the theoretical methods have inherent limitations in accurately predicting the stiffness and stress-strain distribution because of the complex microstructures for 3D braided composites. On the contrary, Finite Element (FE)method possesses obvious advantages over these theoretical methods in terms of investigating the overall and local behaviors of 3D braided composites.10-15The development of FE method is based on a reasonable assumption that the multiscale structure of 3D braided composites exhibits clear periodicity.16,17Therefore, it is possible to develop the numerical modeling strategies using the Representative Volume Elements(RVEs),which are constructed from the microstructures of 3D braided composites.Zeng et al.13developed a numerical model to predict the stiffness and the local stress distribution under longitudinal stress within 3D braided composites. In their study, the prediction of elastic constants was consistent with the experimental results. This numerical modeling method set the foundation for future works, but the proposed model was too simple to represent the real structure of 3D fourdirectional braided composites. A novel parameterized model was developed by Li et al.14to represent the spatial configuration of the braiding yarns and to reflect the real deformation of cross section during the braiding process. Nonetheless, the parameterized model was incredibly time-consuming. Xu et al.15predicted the elastic properties of 3D braided composites via two-scale method (i.e.mesoscale and macroscale), and the obtained results exhibited good agreement with the experimental measurements.Based on the meso-macro scale modeling strategy,several FE models were established to investigate the effects of the braiding parameters on the mechanical properties. Because of the limited number of the data points, the analysis of the effects was rough and localized. Aforementioned studies indicate that the FE method is an effective tool to predict the mechanical properties of 3D four-directional braided composites.

With the increasing application of 3D braided composites in aeronautic structures,18-22more kinds of microstructurebased models with various technical parameters are used to characterize their mechanical properties. Thus, the demand for a database of the elastic constants for 3D braided composites is growing. Unfortunately, for this purpose, FE method requires a huge quantity of multi-scale models to be constructed and computed, which will cost enormous amount of computational expense and time.Therefore,there is a necessity to further develop a Reduced-Order Modeling (ROM)approach to predict the mechanical properties for 3D braided composites.

For aforementioned reasons, a surrogate-based model is proposed as an accurate and computationally inexpensive alternative to predict the mechanical properties of 3D braided composites. In the recent literature,23-28surrogate model was successfully used to reduce computing time and experimental cost. Hou et al.24provided a bi-level reduced surrogate model to identify the material parameters of ductile fracture criterion combining Diffuse Approximation and successive DOE. By introducing the identified material parameters into the numerical simulation, the predicted load-displacement curves concurred the measured results. Thus, the method was confirmed to be computationally robust and affordable. Xia and Breitkopf25constructed a surrogate model to alleviate the heavy computational demand in solving the microscopic boundary value problems.Said and Hallett26developed a multiscale modelling approach which employed a surrogate model considering the mesoscale defects and features in a macro-scale simulation of thick composite structures. A good agreement was obtained between the multi-scale approach and the more computationally expensive high-fidelity models. It indicates that the surrogate-based-modeling approach shows great accuracy in these numerical applications.In order to construct surrogate model properly, the Diffuse Approximation method29,30is widely used. And, its specialized features highlight its validity in a range of numerical applications.31,32Consequently, in this study, a surrogate model based on Diffuse Approximation is proposed to estimate the mechanical properties of 3D four-directional braided composites. This study focuses on deriving the training data using multiscale modeling strategy and the construction procedure of the surrogate model. Furthermore, with the knowledge of the surrogate model, the effects of the technical parameters on the elastic properties are discussed in detail.

2. Multiscale models to predict mechanical properties of 3D braided composites

2.1. Multiscale models

2.1.1. Microscopic model

Commonly, in micro scale, each yarn within braided composites consists of several individual fibers embedded into epoxy resin. To predict the mechanical properties of a given impregnated yarn,an ideal microscopic model is constructed,according to the assumption that the cross-section of a fiber is a circle, and fibers are hexagonally arranged,33as illustrated in Figs.1(a) and(b).Moreover, as shown in Fig. 1(c),the geometry parameters(the length of the microscopic model l and the thickness of the microscopic model t) and the yarn packing factor ε are given by34:

where w is the width of the microscopic model and r is the radius of the fiber’s cross-section.

The carbon fibers and matrix are discretized by the tetrahedral elements(C3D4),as shown in Fig.2.The FE model of the microscopic RVE contains 8799 elements and 599 nodes. To ensure the periodicity of the microstructure, the mesh nodes at two paired boundary surfaces must correspond to each other. The material properties of T300 and epoxy matrix are listed in Table 1.15Exand Eyare the elastic moduli in x and y directions, Gxyand Gxzare the shear moduli in xy and xz directions, respectively.

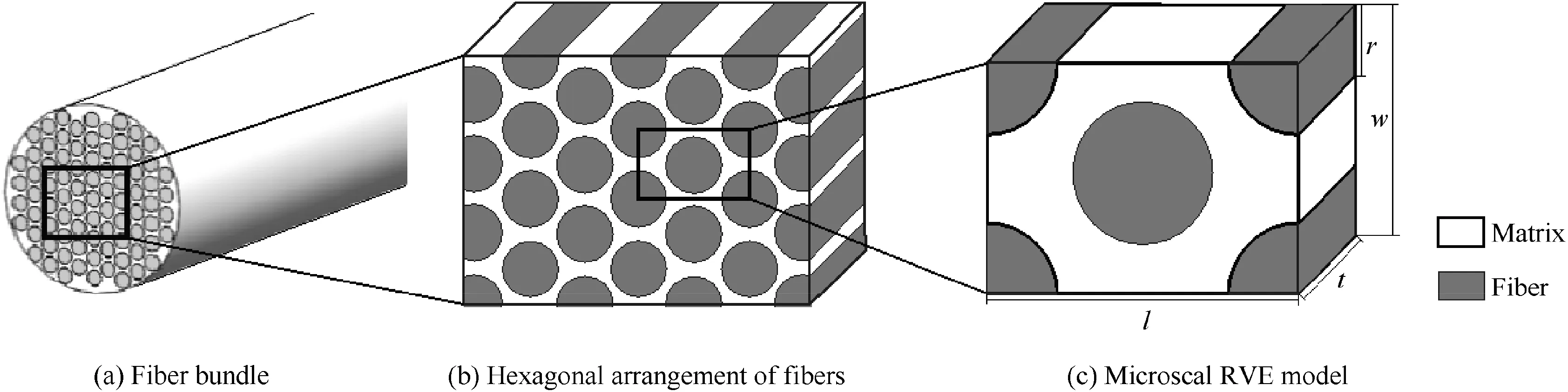
Fig. 1 Geometrical illustration of microscale RVE construction for a fiber yarn.

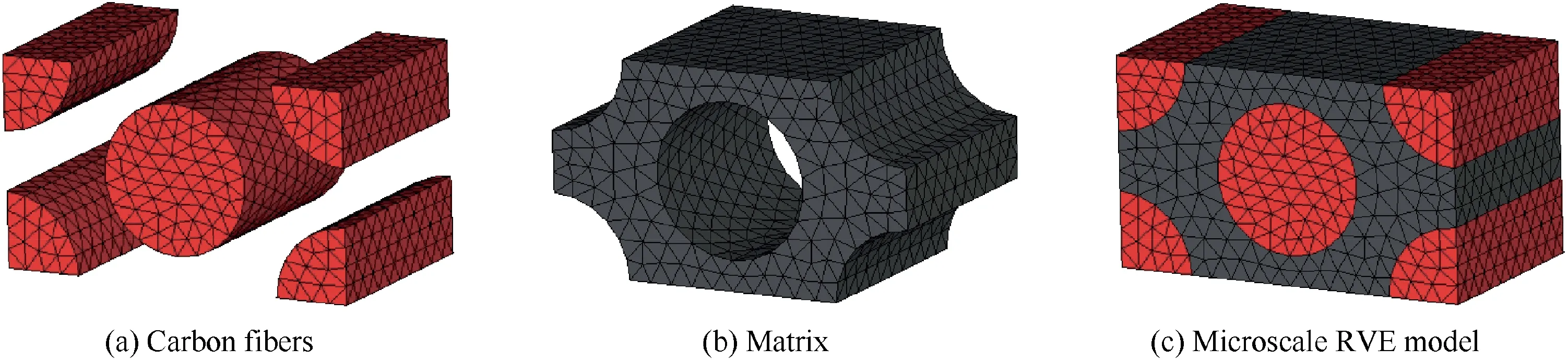
Fig. 2 FE model of RVE for fiber bundle.

Table 1 Mechanical properties for carbon fiber and matrix resin.15

2.1.2. Mesoscopic model

In terms of the 4-step braiding procedure, the macroscopic structure of 3D braided composites can be considered as a topology structure of mesoscopic RVE due to the periodic arrangement of yarns. Moreover, the microscopic structures can be divided into three kinds of RVEs, i.e. the interior, the surface and the corner ones.35However,the corner and surface regions can be ignored because of their small proportion in the macroscopic structure. Fig. 3(a) demonstrates the schematic illustration of the construction process for the interior RVE model. The interior braiding angle γ, the width W and the height h can be measured from experimental observation.Based on the geometric analysis, the relations between these technique parameters are given by12:

where α is the braiding angle of the 3D braided composites,and 2b is the width of the yarn’s cross-section.

Accordingto the braidingprocedure,35the yarns are straightened and deformed during the tightening process.Thus,the following assumptions are used to establish RVEs of 3D braided composites:(A)the braiding procedure keeps relatively steady so that the braided structure is uniform; (B) the cross-section of fiber bundle is assumed to be an octagon with an inscribed ellipse, as shown in Fig. 3(b); (C) the fiber is considered to be transversely isotropic,and the matrix is isotropic.On the basis of mesoscopic observations of the yarn’s cross-section,the relationships between braided parameters and cross-section parameters(the maximum height of the octagon Lm,two sides of the cross-section Laand Lb)are given by12:

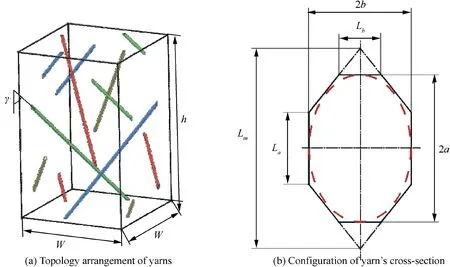
Fig. 3 Illustration of mesoscale RVE model (the red dashed line in (b) represents the inscibed ellipse).

Fig. 4 FE model of 3D four-directional braided composites.

Due to the complex structure, the fiber bundles and matrix are discretized by the tetrahedral elements (C3D4) as illustrated in Fig. 4. The dimension of the mesoscopic RVE for 3D four-directional braided composites is set as 2.21 mm× 2.21 mm× 3.83 mm which is consistent with the No. 2 specimen in Section 4.2.1. Because the predictions of the elastic constants are affected by the mesh size, different mesh size are utilized in HyperMesh and employed in ABAQUS to verify the mesh size convergence.And,the results indicate that the effect can be neglected when the mesh size reaches less than 0.02 mm. For the purpose of reducing computational cost and ensuring the computation quality, the mesh size of mesoscopic model is finally set to approximately 0.02 mm. The FE model contains 31909 elements and 6481 nodes.In the mesoscopic model,the mesh nodes at two paired surfaces are corresponding to each other to ensure the continuity and periodicity of the meso-structures.

2.2. Prediction of elastic properties of 3D four-directional braided composites

In order to ensure the continuity of the displacement and traction at boundary surfaces of the microscopic and mesoscopic RVEs, the Periodic Boundary Conditions (PBCs) are used to perform the different loads on RVEs. Based on the formulas from Xia et al.,36a Python script is written to apply the PBCs at symmetrical mesh nodes between the parallel planes.

To predict the effective elastic properties of 3D braided composites, a homogenization-based approach is developed to compute the overall stress components of the microscale and mesoscale RVEs, given by15:

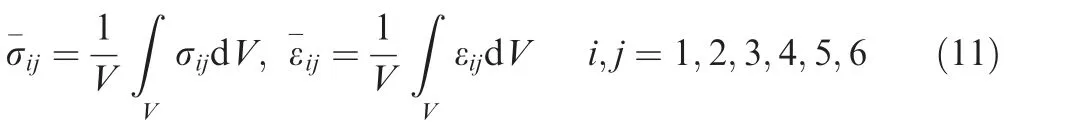
where V is the volume of the microscopic or mesoscopic RVE,σ-ijand εijare overall average stress and strain components,respectively.Generally,the microscopic and mesoscopic RVEs are considered as anisotropic materials, and then the stressstrain relationship can be given by:

where Sijis the compliance coefficient.

Based on the relationship between the compliance coefficients and the engineering elastic constants, the elastic constants of 3D four directional braided composites can be calculated by:

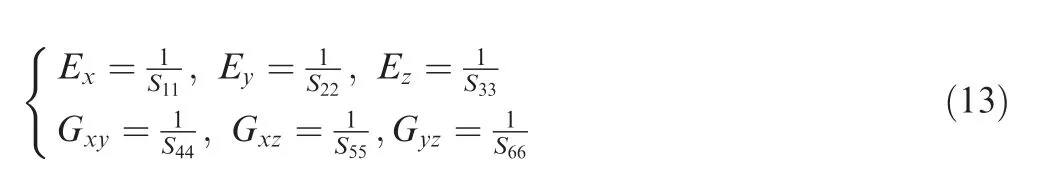
3. Surrogate modeling for elastic properties of 3D four-directional braided composites

In this section, a surrogate-based modeling strategy is developed using the Diffuse Approximation approach37to approximate the mechanical properties of 3D four-directional braided composites.

3.1. Mesostructure design parameters of 3D four-directional braided composites

For the purpose of establishing surrogate models of elastic properties for the 3D four-directional braided composites,the mesostructure design parameters have to be selected. As presented in Section 2.1.2, the interior braiding angle γ (given in Eq. (4)) and the half width of the octagon cross-section b(given in Eq. (5)) play indispensable roles in the construction process of the mesoscopic RVE model. Furthermore, Vfis a key design parameter that significantly impacts the mechanical properties of composites.15In consequence,these three parameters (γ, b and Vf) are considered as the design parameters to construct the surrogate models of elastic properties for 3D braided composites.

After deriving these design parameters of mesoscopic RVE,a feasible region is required to be defined for each parameter to create the DOE space for the surrogate models of elastic constants. Limited by the current manufacturing conditions, the interior braided angle γ is difficult to exceed 54.7°.38Thus,considering the convenience of modeling, the range of α is finally determined as [15°,45°]. Moreover, in order to consistent with the parameter of the specimens in our future works, the varying range of parameter b is finally defined as [0.3, 0.8] (unit:mm). The boundaries of the design parameters are not only determined by the current manufacturing conditions, but also the mesoscopic model in Section 2.1.2. In this model, the fiber volume fraction(Vf)is determined by the yarn packing factor ε in Eq. (3) and the height of the yarn’s cross-section 2a in Eq.(9). Once the yarn packing factor is determined, the range of Vfis finally determined as[0.42,0.51]according to the calculation.Within the varying ranges of these design parameters,the Latin Hypercube Sampling (LHS) approach is used to populate the training points to construct the surrogate models.Fig. 5 shows the design space boundaries and the training points.

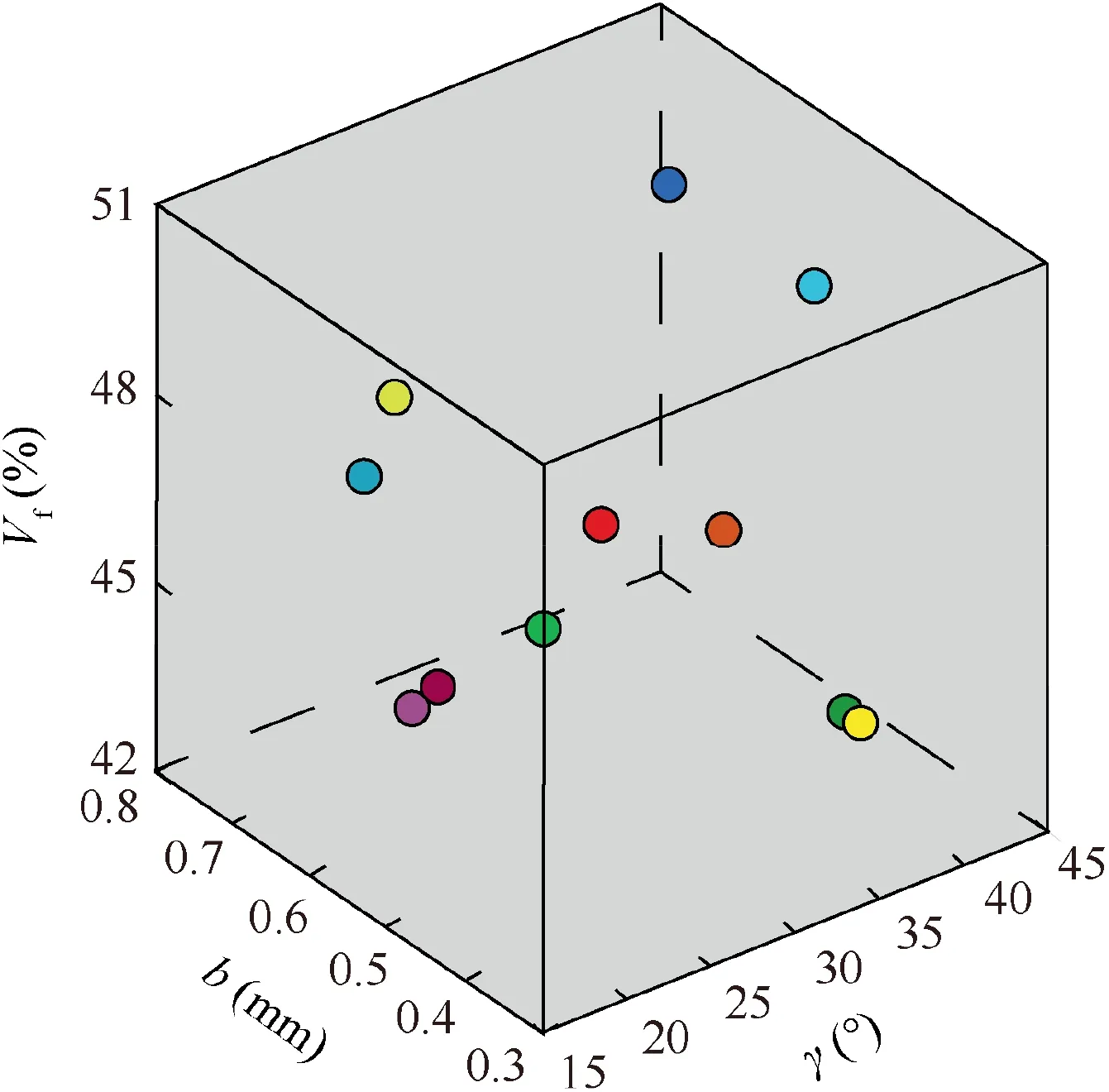
Fig. 5 DOE space of three design parameters and the training points selected using LHS approach.

3.2. Reconstruction of surrogate models using Diffusion Approximation

The elastic properties of the mesoscopic RVEs which correspond to these training points chosen in design space, are predicted using the FE models presented in Section 2.Subsequently, the surrogate models of the elastic properties have been reconstructed using Diffuse Approximation29in this work. The surrogate models can be written as follows:

where ‖x-xc‖ is the Euclidean distance between the estimated point x and the training point xc. And σ is a fixed parameter reflecting the anticipated spacing between the training points.

An illustrative diagram of this interpolaion approach is given in Fig.6.The value of each training point is derived from the prediction of the FE model. It can be seen that the estimated values for the whole design space are locally interpolated using Diffuse Approximation. Once the surrogate models have been constructed, the corresponding elastic constants can be interpolated for any given admissible value of x-x*.Therefore,we reconstruct surrogate models of mechanical properties for 3D four-directional braided composites within the whole design space.

4. Results and discussion

4.1. Surrogate models of mechanical properties of 3D braided composites

Based on the methodologies proposed in previous section, a quadric polynomial basis given in Eq.(15)is used to construct the surrogate models. Moreover, 11 training points generated by LHS approach are chosen from the design space to ensure the accuracy of the models.It is worth to mention that an extra training point (the 11th training point) is selected to prevent the existence of outliers in these training points, which may result in no solution to the problem. The elastic constants of these 11 training points are calculated and listed in Table 2.As a result of the geometrical symmetry of the mesoscopic models, Eyand Gyzare roughly equal to Exand Gxz,respectively.

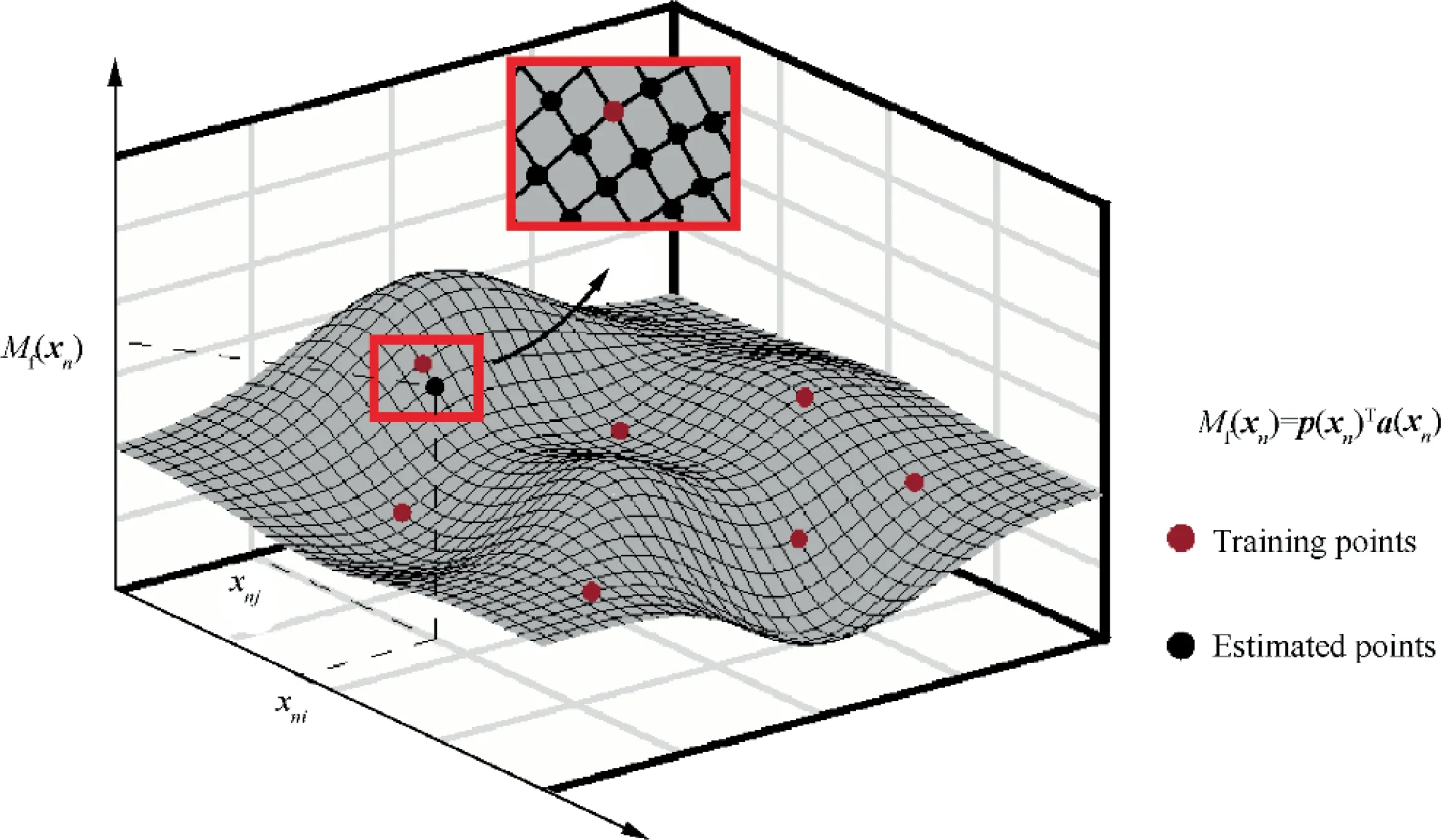
Fig. 6 Illustration of Diffuse Approximation approach used to build surrogate model of elastic properties prediction.

Using the approach mentioned in Section 3.2,the surrogate models of the elastic constants for 3D braided composites are constructed within the design space of various technique parameters as shown in Fig. 7. For the samples with the identical γ and b, transverse stiffnesses increase with the rise of Vfas shown in Fig. 7(a). From Fig. 7(b), the color of the dots changes along the γ axis,it indicates that γ has a greater influence on longitudinal stiffnesses. The longitudinal stiffness of samples reaches maximum when γ is about 15°.As γ continues increasing,the longitudinal stiffness of 3D braided composites tends to the stiffness of matrix and reaches minimum in the cases that γ is about 15°. Obviously, as shown in Figs. 7(c)and (d), the opposite situation has occurred. The increasing tendency of shear stiffness remains for the whole growth process of γ.Detailed analysis of the effects of three parameters on the elastic constants is discussed in Section 4.3.

4.2. Validation of the robustness

The constructed surrogate models, deriving from FE data points, aim to predict the stiffness of the 3D braided composites in an efficient and accurate manner. In order to study the reliability of this proposed method, the inaccuracy of the FE models and surrogate models are examined.

4.2.1. Inaccuracy of FE model

For the purpose of validation, it is necessary to compare the elastic properties acquired from the FE predictions and experiments. Three typical specimens are selected from the study of Chen et al.39The geometry information of these specimens is 250 mm× 20 mm× 6 mm. The technique parameters of specimens are listed in Table 3. Three multiscale models are established according to the numerical modeling strategy mentioned in Section 2.1.Taking the specimen No.2 as an example,the von Mises stress distributions under six different loads are obtained, as shown in Fig. 8.

The prediction of the elastic constants is obtained using the approach mentioned in Section 2.2. Table 4 gives the comparison of Ez, μxzand μyzbetween the experimental measurements39and the predicted results. For the longitudinal stiffness Ez, the maximum deviation between the experiment result and FE method result is 9.86%,and the minimum deviation is only 1.29%. In all specimens, the predicted Poison’s ratios μxzand μyzare smaller than the experimental results.One primary reason is that the study focuses on the interior RVE, while the surface and corner ones are not considered.

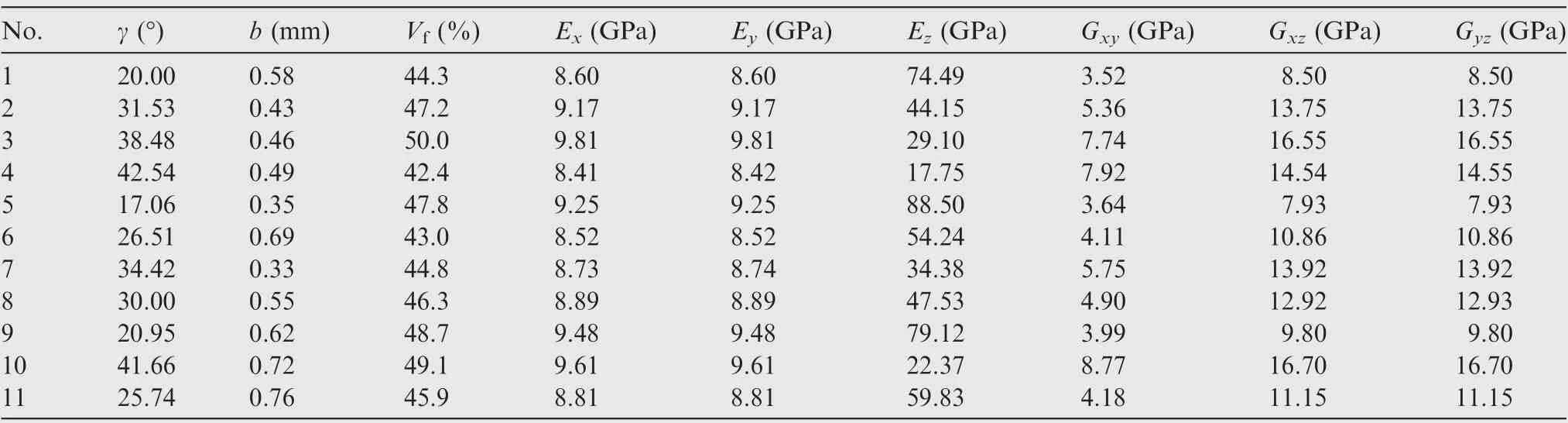
Table 2 Predicted results of training points.

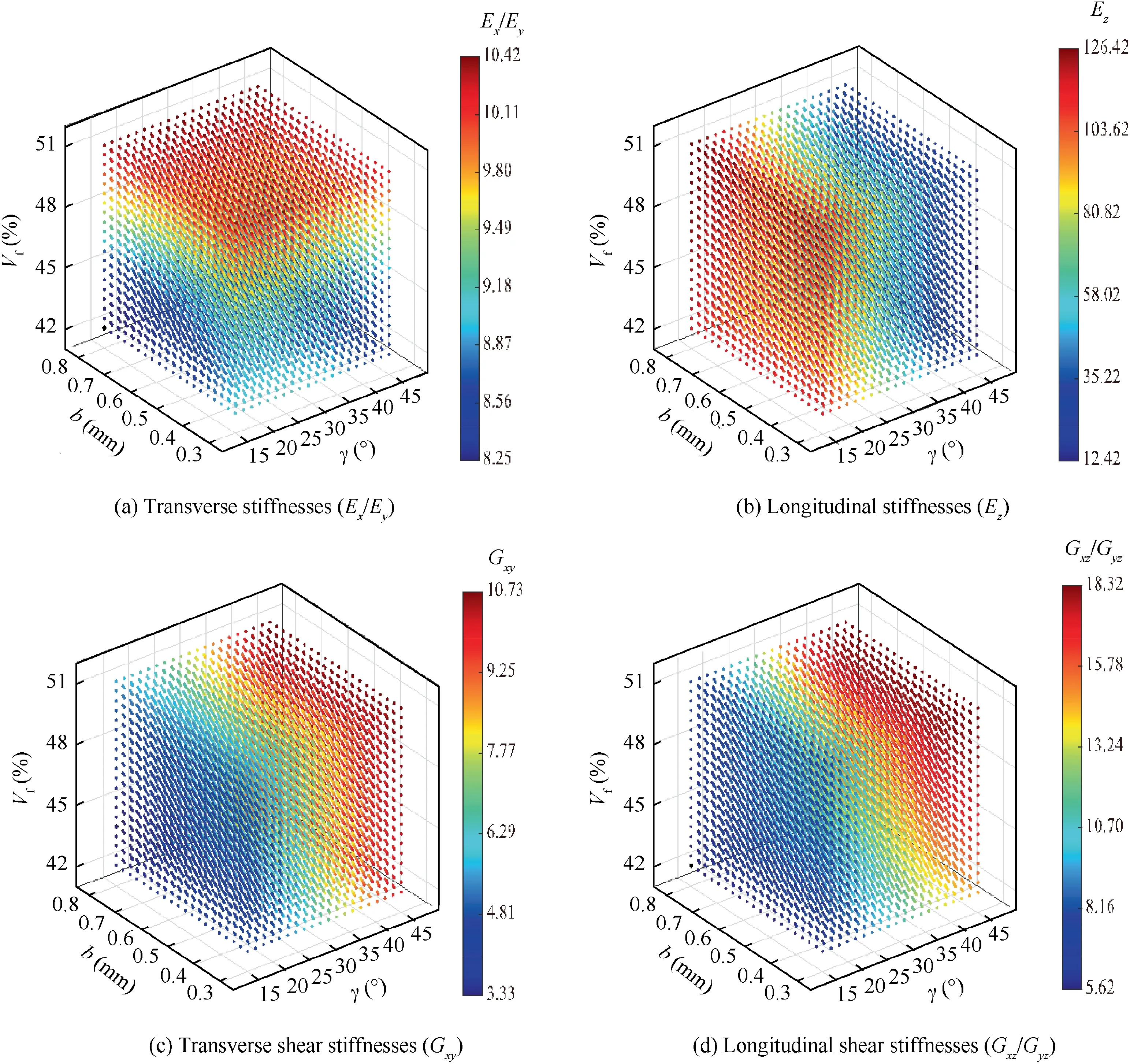
Fig. 7 Surrogate models of elastic properties of 3D four-directional braided composites within design space of various technique parameters.

Table 3 Technique parameters of specimens.

In order to further validate the FE model,two uniaxial tensile specimens of 3D four-directional braided composites are tested. The dimension information of the specimens is 250 mm× 20 mm× 5 mm. The materials used for fabricating the specimens are 12 K T700 carbon fiber tows and TDE-86 epoxy resin. And the technique parameters of the samples are: γ=30.5°, Vf=50.2% and b=0.453 mm. The quasi-static tensile tests, under the room temperature, are carried out at a speed of 1 mm/min.Therefore,two load-displacement curves are obtained as shown in Fig.9.It can be seen that the curves are linear at the beginning, and with the accumulation of damage,the samples finally lose their loading capacities at the load of 109 kN.The average experimental result of longitudinal stiffness is 26.78 GPa. And, the corresponding prediction of the longitudinal stiffness using FE method is 29.13 GPa. The deviation between two results is 8.77%, which indicates the FE method is an effective and accurate way to predict the mechanical properties of 3D four-directional braided composites.

4.2.2. Inaccuracy of surrogate model

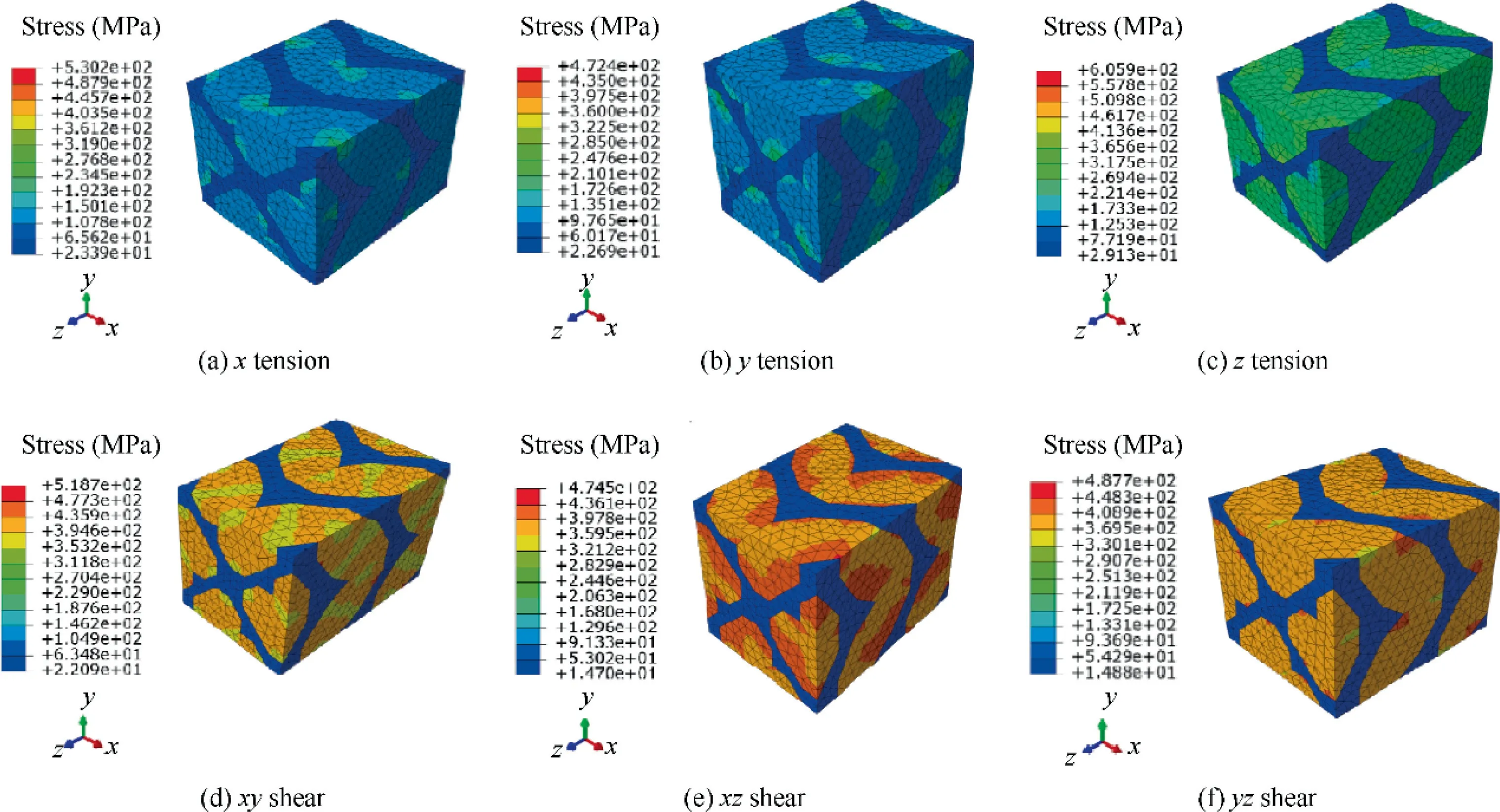
Fig. 8 Von Mises stress distributions within RVE model of No.2 specimen under various loading scenarios.

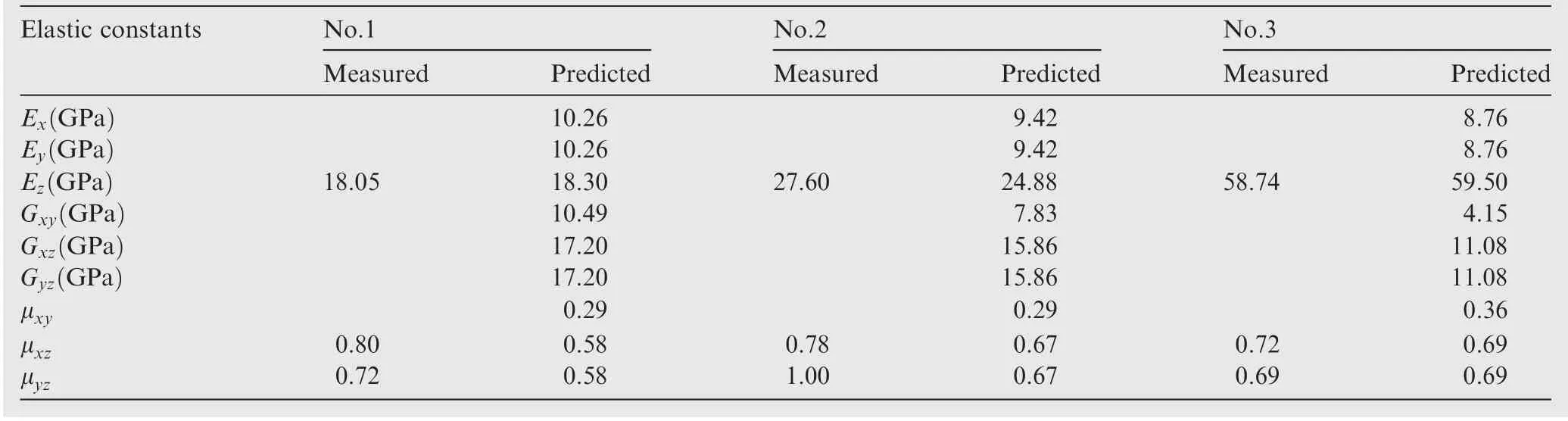
Table 4 Comparison between predicted results and the experimental measurements[39].

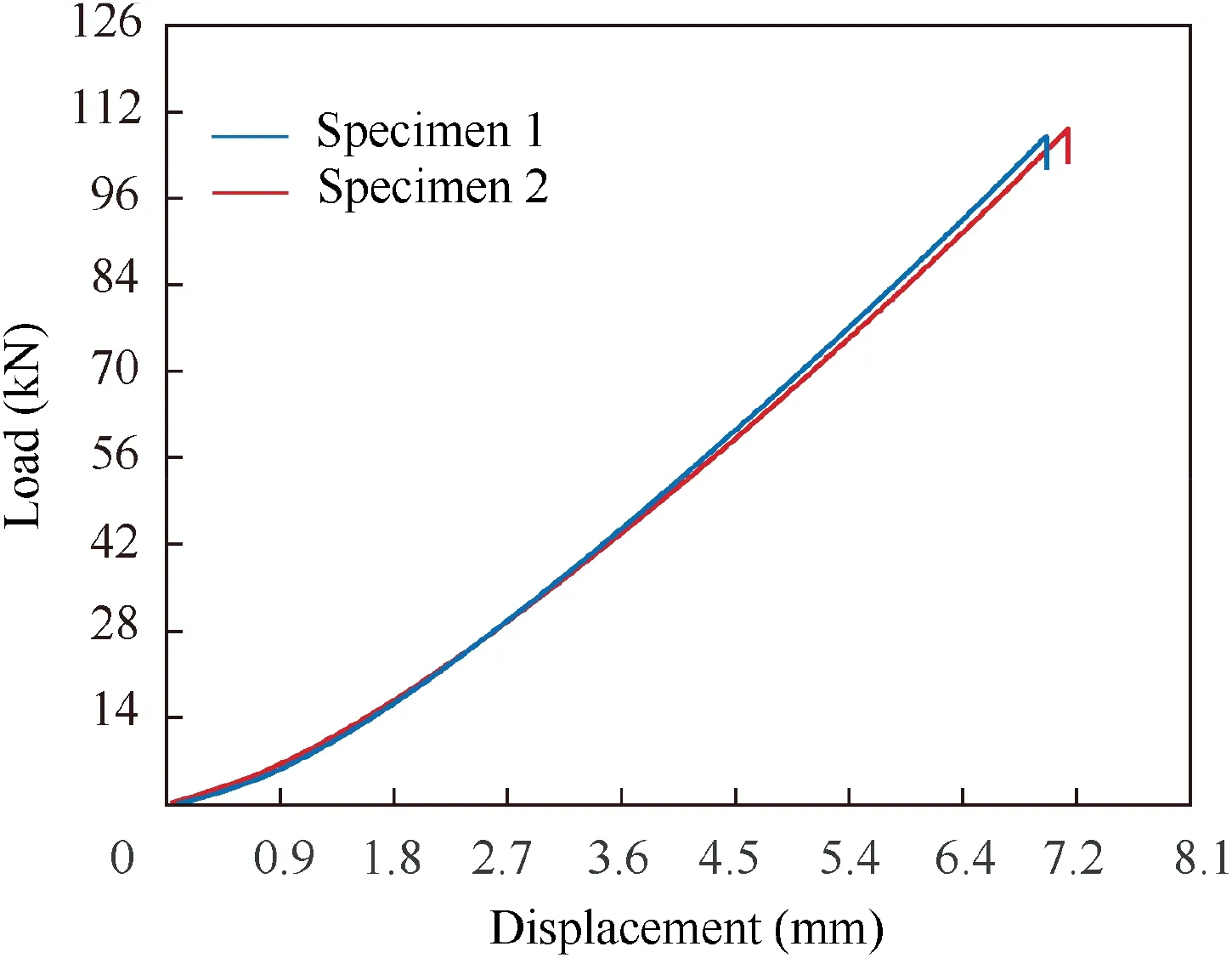
Fig. 9 Load-displacement curves of two specimens in longitudinal direction.

In this study,surrogate models of elastic properties of 3D fourdirectional braided composites are constructed using Diffusion Approximation. Thus, the inaccuracy of the reconstruction approach needs to be discussed. The error estimation procedure consists of following steps: (A) derive testing points in surrogate model randomly; (B) construct multiscale models using the design parameters at the testing points; (C)compare the elastic constants obtained from the surrogate models and FE models.

Based on the aforementioned procedure,four testing points are selected as listed in Table 5.Subsequently,the corresponding FE models are constructed by using the numerical modeling strategy. The relative errors between the surrogate models and FE predictions are expressed as:

where riand ri*denote the approximations from the surrogate model and FE model prediction, respectively. Finally, theresults of relative errors are shown in Fig. 10. In Fig. 10, only slight relative errors (no more than 4.0%) are observed for elastic properties of four testing points.

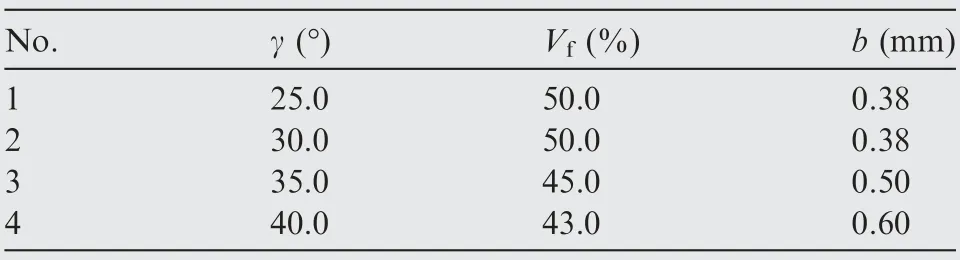
Table 5 Technics parameters of testing points.

Moreover,for a more detailed analysis of the inaccuracy of the surrogate model, the results obtaining from the surrogate model whose technique parameters are consistent with the No.2 and No.3 specimens in Section 4.2.1 are listed in Table 6.The deviation between experiment measurements39and predicted results for two samples are 6.12% and 0.6%, respectively. The above results exhibit that the surrogate models are validated for the prediction of elastic constants of 3D four-directional braided composites.

4.3. Effects of design parameters on the elastic properties

Since each surrogate model is four-dimensional, a series of projected gradient vector maps are depicted in Figs. 11 and 12 to illustrate the effects of three parameters (b, γ and Vf)on the elastic properties. In these gradient vector maps, the arrow points are in the direction of the greatest increasing rate of the elastic constants and the length of arrow represents the relative value of gradients.

Figs. 11(a) and (b) present the variation of transverse stiffness within the varying ranges of b and Vf, γ and Vf, respectively. All the vectors in both figures are obviously parallel to the Vfaxis,which means Vfhas a greater influence on transverse stiffness than parameters b and γ.Due to the impact of Vfis too enormous to observe the effect of the other two parameters,variation of transverse stiffness within the varying ranges of γ and b is shown in Fig.11(c).The direction of the arrows in Fig. 11(c) is downward, it indicates that transverse stiffness decreases steadily with the increase of parameter b. For the specimens with the identical b, when γ is between 15° to 25°,transverse stiffness increases as γ becomes larger. However,in the case that γ exceeds 25°, transverse stiffness decreasesrapidly. The red arrows in the blue box in Fig. 11(c) indicate the solutions for the interior braided angle which makes the transverse stiffness reach the highest value. The arrows distribute on both sides of γ=25°as parameter b increases from 0.3 mm to 0.55 mm,which means the optimal solution changes as parameter b increasing.

Table 6 Comparison of results obtained by experiments39 and surrogate model.

As shown in Fig. 11(d), the angle between the arrows and the b axis is almost 45°. The interesting observation reveals whether b or Vfincreases, longitudinal stiffness increases steadily. It should be noted that with the raising of Vf, the arrows are stretched. The phenomenon demonstrates that the influence of Vfon longitudinal stiffness becomes more significant.The arrows in Figs. 11(e)-(f) are roughly parallel to the γ axis.It indicates that comparing with b and Vf,γ has a more noticeable impact on longitudinal stiffness.

The relationship between shear moduli and these three parameters of 3D four directional braided composites are presented in Fig. 12. Fig. 12(a) shows transverse shear stiffness and Vfare positively correlated. Furthermore, the change of transverse shear stiffness caused by the increment of Vfbecomes significant as the length of arrow increases with the raising of Vf. As shown in Figs. 12(b)-(c), the increasing tendency of transverse shear stiffness remains for the whole growth process of γ. Fig. 12(d) demonstrates the influence of b and Vfon longitudinal shear stiffness.It should be noted that longitudinal shear stiffness increases steadily with the decrease of parameter b. On the contrary, for the specimens with the identical b, longitudinal shear stiffness increases obviously as the rise of Vf. Figs. 12(e)-(f) show that as γ increases, longitudinal shear stiffness increases considerably.Comparing with Vfand b, the effect of γ on longitudinal shear stiffness is more significant.

From the aforementioned analysis, it can be found that these three key parameters γ,b and Vfhave effects on the elastic properties of 3D four-directional braided composites.Therefore, the knowledge of the influence of three design parameters provides designers an efficient and accurate way to optimize the structure of 3D four-directional braided composites.

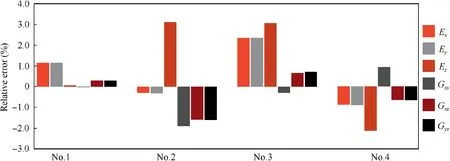
Fig. 10 Relative errors between FE predictions and approximations of surrogate models at four testing points.

Fig. 11 Effect of three design parameters on transverse stiffnesses and longitudinal stiffnesses.

5. Conclusion and perspectives

In this paper,surrogate models derived from a limited number of FE data points have been proposed to predict the elastic constants of 3D braided composites. The main conclusions are as fellow:

(1) The methodologies combined FE method and Diffuse Approximation to construct the surrogate models of various elastic constants of 3D braided composites are developed. Good agreements are obtained between the FE results and experimental measurements. Furthermore, the predictions obtained from surrogate models results concur well with the FE predictions and experimental results. Thus, the proposed surrogate-based modeling strategy ensures the accuracy of the models as well as reduces the computational cost and time.

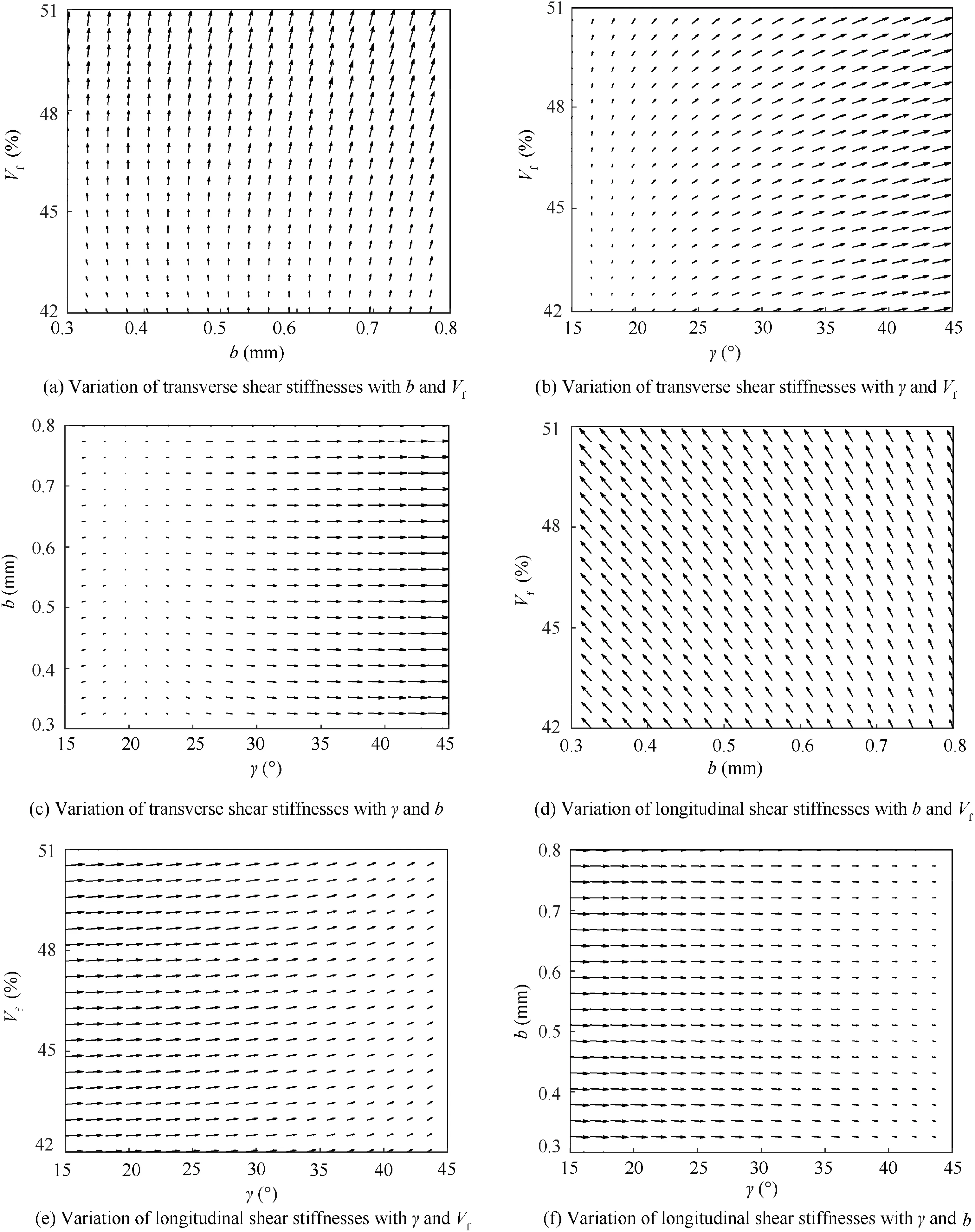
Fig. 12 Effect of three design parameters on transverse shear stiffnesses and longitudinal shear stiffnesses.

(2) The proposed surrogate models provide a database of the whole design space which helps us to analyze the effect of three technique parameters on the elastic constants of 3D four-directional braided composites. In the parametric analysis of parameter Vf,it is found that,Vfhas a greater influence on transverse stiffness than the other parameters.The raising of Vfresults in the increase of transverse stiffness of 3D braided composites.

(3) Comparing with parameters b and Vf,the effects of γ on longitudinal stiffness and shear stiffness are more significant. The increasing tendency of transverse shear stiffness has grown at a phenomenal rate with the increasing of γ. Conversely, the growth in longitudinal shear stiffness decelerates significantly as γ becomes larger. In addition, the effect of parameter b are slight but non-negligible.

More comparisons of the other elastic constants between the experimentalmeasurementsandthepredictedresultswillbeconsidered in our future investigation.Moreover,surrogate modeling techniques lead to a more efficient way to compute FE models,such as multiscale RVE models of 3D four-directional braided composites containing internal defects and features.

Acknowledgements

Authors acknowledge the financial support from National Natural Science Foundation of China (No. U1833116), and the China Postdoctoral Science Foundation Funded Project(No. 2018M642775). This study is also supported by Key Scientific Research Project of Colleges and Universities in Henan Province (No.20A460003).