Light weight optimization of stratospheric airship envelope based on reliability analysis

Yunce ZHANG, Yafei WANG, Changguo WANG,*

a National Key Laboratory of Science and Technology for National Defence on Advanced Composites in Special Environments, Harbin Institute of Technology, Harbin 150001, China

b Center for Composite Materials, Harbin Institute of Technology, Harbin 150001, China

KEYWORDS Failure modes;Mass optimization;Optimal design;Reliability analysis;Stratospheric airship

Abstract A stratospheric airship is an essential flight vehicle in the aviation field. In this paper,optimal design approach of stratospheric airships is developed to optimize envelope shape considering three failure modes and multidisciplinary analysis models,and could also reduce the mass of a stratospheric airship to be deployed at a specific location.Based on a theoretical analysis,three failure modes of airships including bending wrinkling failure, hoop tearing failure and bending kink failure, are given to describe and illustrate the failure mechanism of stratospheric airships. The results show that the location,length and size of the local uniform load and the large fineness ratio are easier to lead to bending wrinkling failure and bending kink failure.The small fineness ratio and the increasing differential pressure are more prone to cause hoop tearing failure for an airship hull.The failure probability is sensitive to the wind field. From an optimization design, the reliability analysis is essential to be carried out based on the safety of the airship. The solution in this study can provide economical design recommendations.

1. Introduction

Stratospheric airships are lighter-than-air vehicles that provide lift by floating gas. Stratospheric airships deployed at the height of approximately 20 km can achieve higher observation resolutions than satellites and this altitude has exceeded the scope of air attacks. In recent years, considering the stable working environment and special working height, the stratospheric airship has become an important stationary platform besides satellites and then many countries have paid attention to the development of stratospheric airships. However, many essential issues related to the reliability of a stratospheric airship still remain unsolved.

In general,stratospheric airships work at the bottom of the stratosphere for a long time. The meteorological condition in this altitude range is relatively stable and there is no complicated weather phenomenon such as rain, snow and fog. Wind load is a major external load for a working stratospheric airship. Zhang and Yang1established the lateral three degrees of freedom dynamic model to consider wind interference. In order to improve reliability, the aerodynamic performance under wind load should be considered for a stratospheric airship which is in working condition for a long time. From energy fuels of a stratospheric airship, nearly 70% of energy fuels are used to overcome aerodynamic drag. Thus, if the aerodynamic drag is reduced, more energy fuels will be used to increase the working hours or improve the extra payload capacity. Compared with other aerospace vehicles, the gravity of a stratospheric airship is more prone to fluctuation with the variation of payload.For a general stratospheric airship,a 5%increase in gravity represents a loss of 20-25%of its payload.2Therefore, it is important to consider the weight reduction of the stratospheric airship.

Over the past ten years,much research has been focused on optimization and design.Several advances3-5performed shape optimizations of airship hulls considering different Reynolds number regimes, while the structural constraints are not considered.In addition,there are many studies on algorithm optimizations of an airship.6-9Kanikdale et al.10carried out optimization for an airship hull using the simulated annealing optimization algorithm, in which optimization variables are the shape parameters of an airship hull.The conceptual design of airships was proposed using basic operating and performance parameters11and concurrent subsystem optimization.12Based on the conceptual design, aerodynamic and geometry parameters were obtained.13Many multidisciplinary design methods were described for determining the optimal envelope shape of an airship, such as environment model, geometry model,aerodynamic model and energy model.14-17Most previous studies have optimization for aerodynamic and geometry parameters. However, when an airship is in working or recycling conditions, the failure status will emerge (such as tear and wrinkle). With regard to the light weight design of an airship, it is illogical to only consider safety without reliability.Furthermore, various failure modes of airships are fundamental in the reliability analysis of airships, whereas the failure mechanism of airships is not involved in previous studies.Despite the extensive study efforts at multi-objective optimization and structural design of a stratospheric airship (e.g. Ref.10) and despite recent advances in design models and optimized models (e.g. Ref. 14), the failure mechanism of airships has still not been elucidated by researchers and some essential issues in regard to reliability based on the failure mechanism of airships in the optimization process remain unsolved. It is significant to consider reliability which is related to many factors and modes of failure based on safety.

In this study,light weight, safety and reliability are considered in the process of analysis, design and optimization of a stratospheric airship. Based on theoretical analysis, three failure modes of airships, i.e., bending wrinkling failure, hoop tearing failure and bending kink failure, are given to describe and illustrate the failure mechanism of airships. Furthermore,a complete and comprehensive solution of optimal design is constructed to reduce the weight of a stratospheric airship in an optimization model. Moreover, considering the probabilistic approach,the proposed solution is demonstrated by means of the specific environmental factor and a real stratospheric airship. The results of this study can promote the systematic development of optimal design against failures of airships and provide design recommendations considering the reliability of airships.

2. Methodology

2.1. Optimal design approach

The optimization problem is formulated as

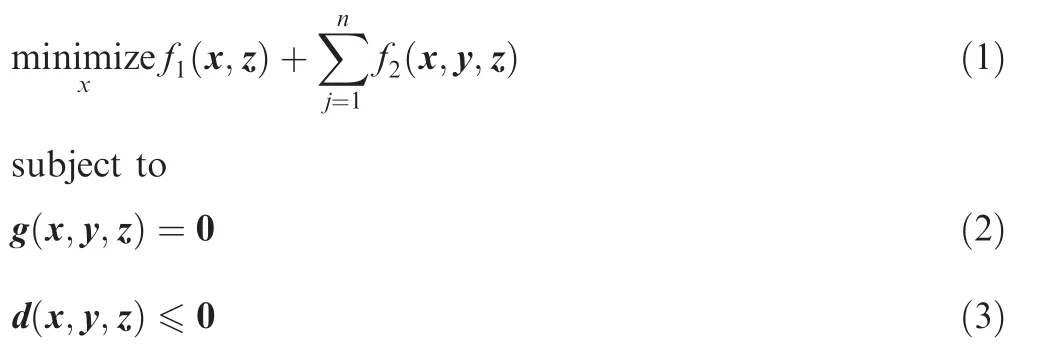
where f1（x，z） represents the structural mass and f2（x，y，z） is the extra mass for failure modes. g（x，y，z） and d（x，y，z） are both equality and inequality constraints. Variables x, y and z are design variables, random variables and auxiliary parameters, respectively. In the extra mass, the process of the probabilistic method of structural reliability analysis related to the rate of failure in one mode of failure is illustrated.18. In the structural mass, the change of structural sizes occurs with a variety of constraints. Each failure mode is determined by a corresponding limit state equation.19

In general,stratospheric airships work at the bottom of the stratosphere for a long time. The meteorological condition is relatively stable and the wind load is the major external load for a working stratospheric airship in this altitude range. The wind is assumed as a static form,and then the maximum wind speed is obtained to carry out calculation and design. Nevertheless, in fact, the wind should be considered as a dynamic process, which can be substituted with statistically significant wind data. Wind occurs randomly and is defined by wind speed, period and height. The statistics are effective for the wind field model.20Previous studies have indicated that the Weibull distribution is more useful for natural winds over longer time periods.21Then the Weibull probability density function can be written as

where vwis the wind speed, and k and c are the shape factor and the scale factor for the distribution, respectively.

Based on the reliability theory,the reliability index and the failure probability are obtained under the condition that the variable follows the normal distribution. Then it is necessary to substitute or approximate the variable from Weibull distribution to normal distribution. Both k and c22are obtained as

2.2. Failure modes

The stratospheric airship has various failure modes to be considered, which include structural instability, envelope tear,propulsion system failure and failures of several other components of a stratospheric airship. However, considering the effect of structural integrity and the simplicity of failure,three failure modes of a stratospheric airship are classified into the optimal design solution: bending wrinkling failure, hoop tearing failure and bending kink failure.

In the failure mode,a discriminant function exists and indicates whether a failure mode has occurred. Nonetheless, it is noted that the threshold criterion only gives a quantitative indicator for the appearance of a failure mode in theory and structural failures do not necessarily lead to the complete destruction of an airship but irreversible structural damage.Failure and damage will affect the working condition of an airship and cause a significant decline in the performance of an airship.

2.2.1. Bending wrinkling failure

In this subsection, the bending wrinkling failure of the main body of an airship(taking Hisentinel80 as an example)is studied. The capsule structure of an airship is a typical thin-film structure. Due to a lack of out-of-plane stiffness, the soft film of an airship is easily deformed by an external load to form a wide range of wrinkles.The wrinkles with stress concentration characteristics change the load path on the surface of the structure, which greatly affects the configuration and vibration characteristics of the structure. In severe cases, the wrinkles may even cause the film surface to rupture until it cannot work. The local uniform load is considered to apply on the hull,where the envelope can be wrinkled easily.The main body model of an airship is shown in Fig. 1. It is assumed that the model is simply supported on the head and tail. For a stratospheric airship, there are some indispensable parameters to be given in the method, such as a1and a2are the lengths of the semi-major axis of the two ellipsoids, respectively, and s is the length of the cylindrical center section, the local uniform load q,the radius of the central cylinder r,the length of an airship L,and the boundary of the applied local uniform load L1and L2.

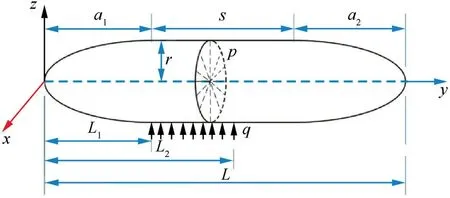
Fig. 1 Main body model of stratospheric airship.

According to the influence of the external load and boundaries, the structural moment M23is expressed as

2.2.2. Hoop tearing failure

Generally,the envelope material of a stratospheric airship is a multilayer film laminate. Under the influence of the internal pressure, the capsule structure of an airship can be deformed and the envelope can be seen as being in the planar stress state.Therefore, the envelope is subjected to axial stress and hoop stress. The axial stress σpxand the hoop stress σpθprovided by Ref. 23 are as follows:

Obviously,the hoop stress can preferentially reach the yield strength σs. Hence, the limit state equation is expressed as

2.2.3. Bending kink failure

When the uniform load increases to a critical value, a large deformation appears in the body of a stratospheric airship.Meanwhile, two adjacent wrinkling peaks are close to each other and the surface tensile stress on the opposite side of the wrinkled area occurs and reaches its limit. At this point,the structure can be seen as a plastic hinge,and kink is considered to appear on the airship. Noted that if the moment is increased,the membrane entering the plastic stage will be torn and the structure will be invalid completely.

2.3. Description of design models

2.3.1. Wind field model

There are many different types of airships used in various environments to realize different functions. The environment is complicated and susceptible to height and location. However,compared with the troposphere and the ground, the stratospheric environment is relatively stable, where the wind is the major environmental factor. The direction and magnitude of ambient winds can play an important role in wind field analysis.

Ambient wind speed in the stratosphere is related to altitude,location and time,and it maybe has a different value with the changes of altitude, location and time. In general, the working altitude range of stratosphere airships is 17 km to 25 km and wind direction is the zonal wind along east-west direction without taking the meridional wind along a northsouth direction into account at the operating altitude. In this study, the wind field model is assumed as a random process.As we can see from Fig. 2, the wind field fitting surface based on the change of zonal wind components for the period at various altitudes is illustrated.16

2.3.2. Geometry model

At present,the rotating hull shape is widely used in the design of a stratospheric airship. The traditional shape is a double ellipsoidal hull composed of two semi-ellipsoids.In this paper,as shown in Fig.1,HiSentinel8024in the HiSentinel program is used as the original geometry model.Compared with the traditional hull, the cylindrical shape is added at the maximum thickness location between two semi-ellipsoids.

2.3.3. Aerodynamic model

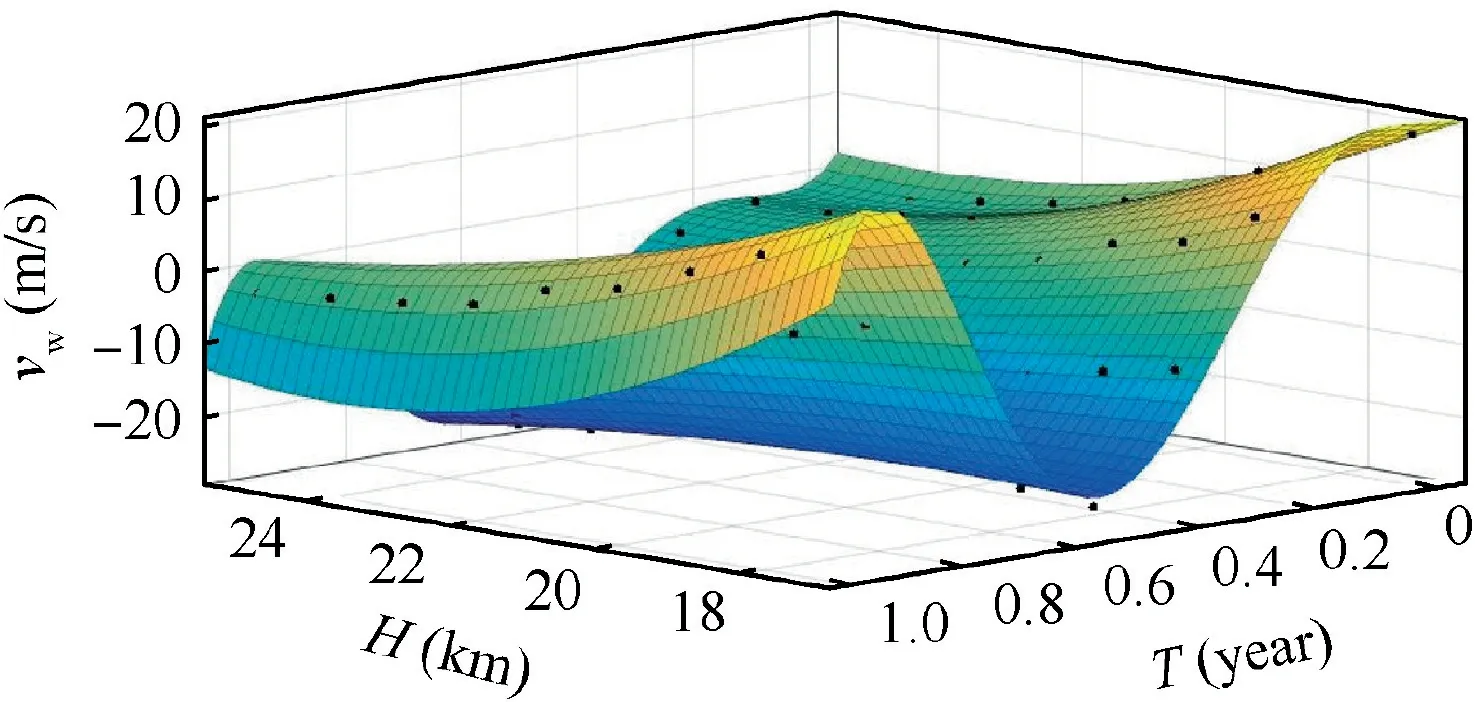
Fig. 2 Fitting surface of wind at various altitude.

In the design of a stratospheric airship, the aerodynamic drag is evaluated by the aerodynamic drag coefficient and the control system is initially selected. Based on wind tunnel test data and theoretical analysis results, the aerodynamic drag coefficient is calculated using an estimation formula2which can be expressed as

where ρ is air density,vais airspeed,μ is the dynamic viscosity coefficient, R0is earth radius 6378.5 km, and h is airship height.

Based on the results of theoretical analysis and wind tunnel test data, Yang and Liu14suggested that the drag coefficient(Cd) of the airship body is 55% of the total drag coefficient.The total drag coefficient (CD) can be written as

It should be noted that the stratospheric airship is imaged to adopt a fixed-point wind resistance strategy. The strategy is that the head of the airship faces the wind and both the airspeed and wind speed are equal.14

2.3.4. Mass model

For a stratospheric airship, the envelope mass and the helium gas mass are the majority of the total mass.2For simplicity,only envelope mass and helium gas mass are considered in the mass model, and the volume of a stratospheric airship can be approximated as a combination of two semi-ellipsoids and one cylinder.

The helium gas mass can be expressed as

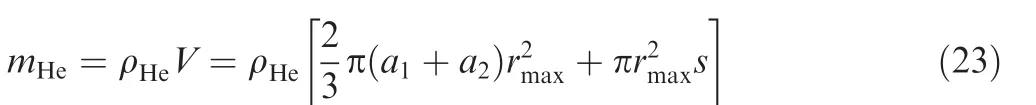
where V is the volume of the stratospheric airship, ρHeis the density of the helium gas, rmaxis the maximum radius of the airship, and s is the length of the cylindrical center section.

Considering the actual manufacturing process and the size level of the stratospheric airship to design,14the envelope mass can be expressed as

where ρenvis the density of the envelope and S is the surface area of the airship.

Therefore,the main mass of the stratospheric airship can be written as

3. Analysis and discussion of probability effect

To reduce the structural mass of the stratospheric airship without any failure, three failure modes of a stratospheric airship were considered.The modes of failure were bending wrinkling failure, bending kink failure and hoop tearing failure. The aforementioned equations were used and the optimal design solution was verified with a formulation of the stratospheric airship using a numerical study. In this section, four subsections are involved to illustrate the results and analyses using the optimal design solution for the stratospheric airship.

3.1. Typical failure of stratospheric airship

The failure probability plays an important role in the reliability analysis of a stratospheric airship and the reliability index is related to the failure probability closely. Three typical failure probabilities are given without the remaining parameters changed.From a series of calculations,the following values of reliability indexes and failure probabilities are obtained:βw=0.7193, βh=2.2276, βk=5.2841, Pw=4.7239×10-5,Ph=6.8621×10-4and Pk=4.3071×10-6.The failure probabilities from the different failure modes are useful for the subsequent analysis and discussion.

3.2. Load distribution of airship hull

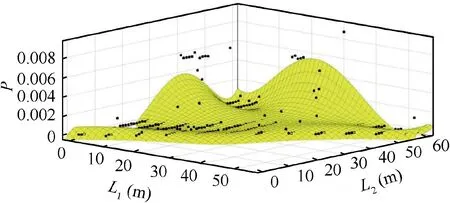
Fig. 3 Failure probability effects for various load distributions.

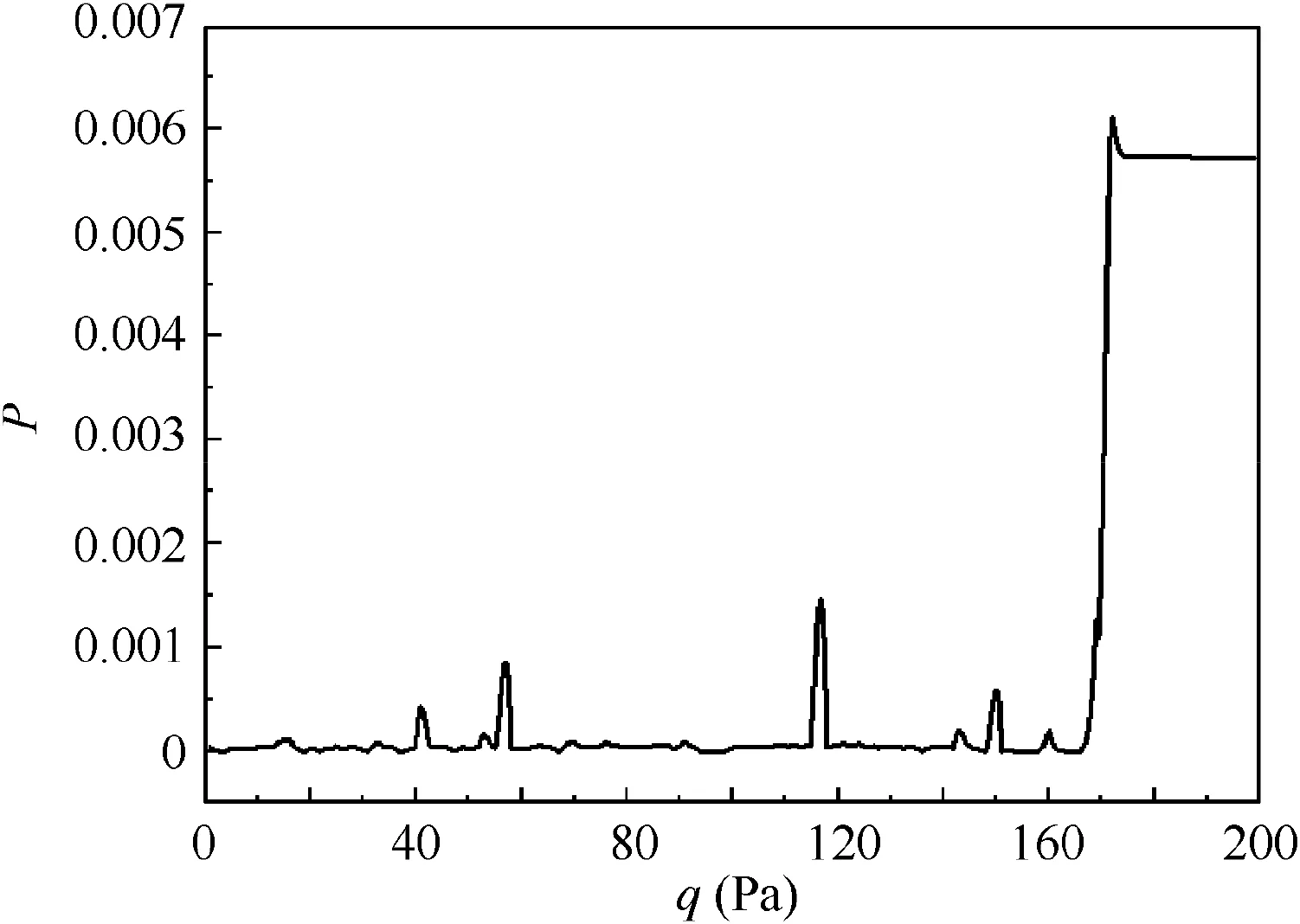
Fig.4 Failure probability effects for various local uniform load.

The external load is an essential factor for the stratospheric airship to cause the occurrence of a failure. As shown in the Fig. 3, when one end of the local uniform load is at the head or the tail of the airship and the other end is closer to the middle cylindrical section, the total failure probability of the airship is larger, that is, the airship is easier to lead to failure.That is because when the aforementioned load distribution situation occurs,the moment M rises gradually with the increase of the length of the load distribution, which leads to the local wrinkles on the surface of the stratospheric airship. As shown in Fig.4,when the local uniform load q reaches a critical value,the failure probability has changed drastically from almost 0 to nearly 0.006. Due to the increasing uniform load q, the whole deflection and potential energy of the airship hull rise.In order to release the energy, local wrinkles appear on the hull of the airship, which leads to an increase in the probability of bending wrinkling failure.

3.3. Wind field characteristics

The wind field is an indispensable factor in the stratosphere,but the variety of the wind field is complicated and uncertain.Generally, the Weibull model is a good approximate distribution for the description of the wind field.19The Weibull distribution can be described using two parameters k and c,where k represents a shape factor and c represents a scale factor in the Weibull distribution. As long as the two parameters are determined, the corresponding distribution can be determined.Thus, with the Weibull distribution determined, a year’s data can approximately simulate the actual wind field to predict yearly or monthly values for other years.

As shown in Fig.5,the failure probability has changed with the change of the parameters. The failure probability is sensitive to the value of c and only a tiny change appears in the failure probability with the change of k value.

3.4. Parameters and service time of stratospheric airship

For the stratospheric airship,the fineness ratio(f)is an important indicator that can affect the aerodynamic characteristics of airships. As shown in Fig. 6, there are many large failure probabilities for the most fineness ratios,and the failure probability is small only when the fineness ratio is in the range of 4.5-4.7. When the fineness ratio is small, it is more prone to cause hoop tearing failure for the airship hull. With the fineness ratio increasing, it is more prone to lead to bending kink failure. Therefore, the reliability of the stratospheric airship is good when the fineness ratio is about 4.5.The differential pressure has an influence on the structural stability, and the shape of the hull is maintained by the differential pressure.The stiffness of the stratospheric airship is completely provided by the inflatable hull,and the load is completely borne by the body of the inflatable hull.With the increasing differential pressure,the change of the failure probability is shown in Fig. 7. With the differential pressure of the airship hull being small, the local wrinkles are easier to appear and bring on bending wrinkling failure and even bending kink failure.With the increase of differential pressure, it tends to cause hoop tearing failure.

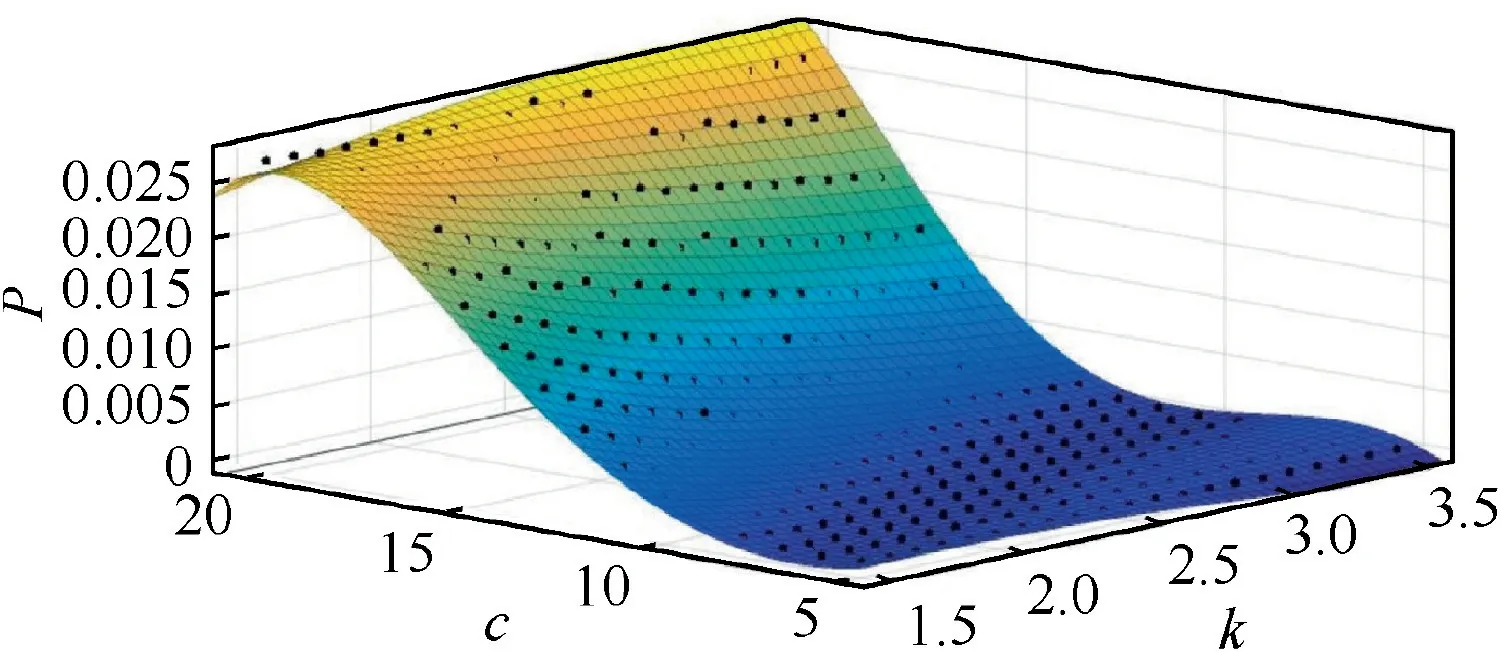
Fig. 5 Failure probability effects for various wind field characteristics.

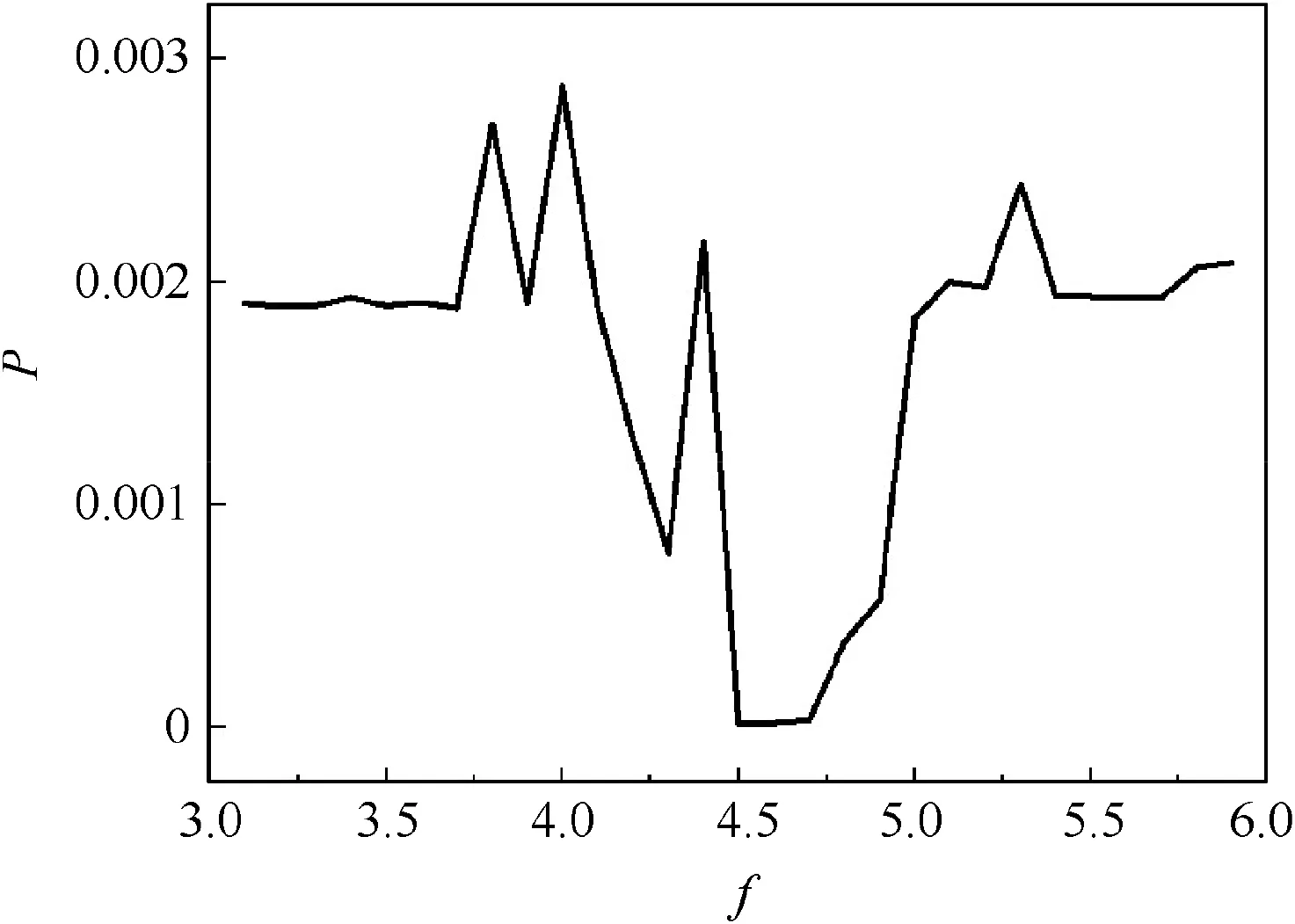
Fig. 6 Failure probability effects for various fineness ratios.

The reliability of the airship can be affected by the mean period of the wind field and the service time of the stratospheric airship directly. As shown in Fig. 8, when the mean period is about 18 months, the linear approximation is established between the failure probability and the service time.With the decrease of the mean period and increase of the value of service time, the failure probability has a small jump.

Fig. 7 Failure probability effects for various pressures.

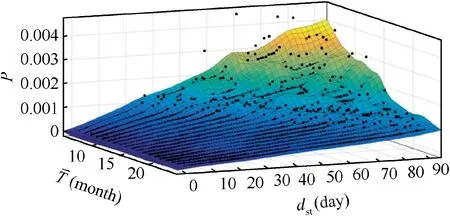
Fig. 8 Failure probability effects for different wind mean periods and service time.

4. Illustration of optimal design

For the sake of generality, the design variables are composed of environmental parameters and structural parameters, such as the local uniform load q and the maximum radius of the airship rmax. The auxiliary parameters mainly include some constants. A detailed description of the parameters is illustrated subsequently.

4.1. Description of variables

4.1.1. Design variables and random variables

In order to illustrate design variables clearly, several design variables for the stratospheric airship with the definition of variables, initial values, lower boundary and upper boundary are shown in Table 1. The initial values of variables represent the design values in the actual project.Considering the limit of structural sizes and actual needs in the engineering project,lower boundary and upper boundary of variables are assumed in a reasonable range.These design variables affecting the reliability of the stratospheric airship can be optimized to reduce the total mass of the airship.

In this study,k and c both selected from the actual situation are 1.5 and 9.4, respectively.19In Table 2, the mean and standard deviation of each distribution are presented.

4.1.2. Auxiliary parameters in formulas

In addition to the important parameters including design variables and random variables, some auxiliary parameters are considered in equations of the optimal design solution. The value and meaning of auxiliary parameters for equations are presented in Table 3.

4.2. Solution of optimal design

Based on the reliability analysis,the optimal design solution is proposed to be applied to the stratospheric airship. The purpose of optimal design is to achieve a balance between performance and mass,which ensures adequate performance to resist winds and has a minimization of the total mass of a stratospheric airship. In the optimal design method, bending wrinkling failure, hoop tearing failure and bending kink failure are included.

Under all these considerations,the optimal design problem can be obtained

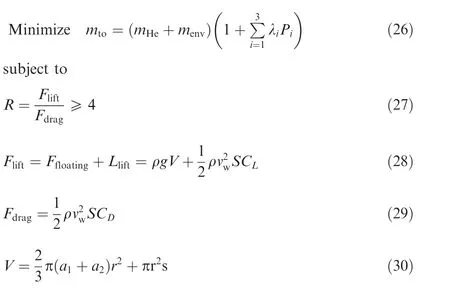
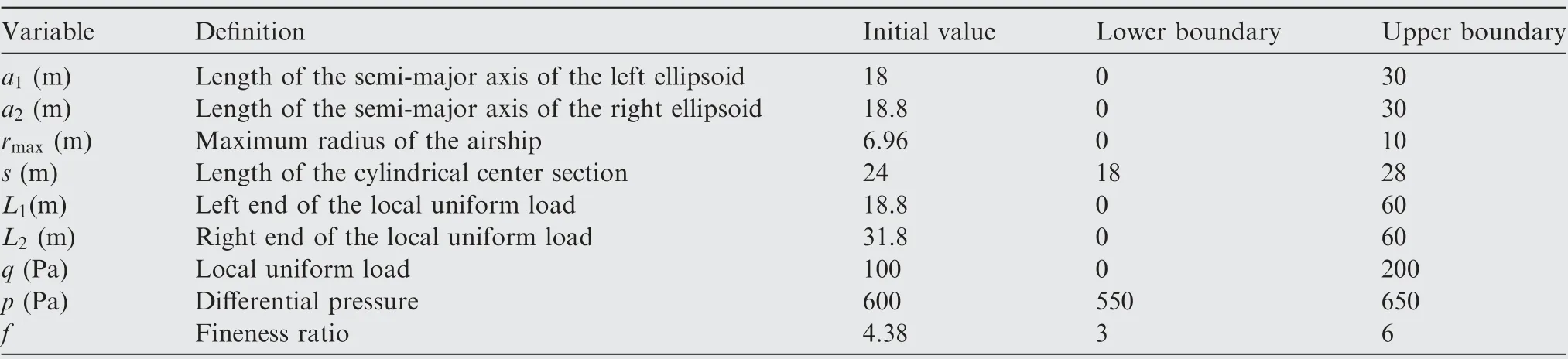
Table 1 Values and meanings of design variables.

Table 2 Values and meanings of random variables.

Table 3 Value and meaning of auxiliary parameters.

where λiis the partial coefficient affecting mass for the different failure modes,Piis the failure probability,i=1，2，3 represent three modes of failure,i.e.bending wrinkling failure,hoop tearing failure and bending kink failure, R is the lift to drag ratio, Fliftis the lift of the airship, Fdragis the drag of the airship, CLis the lift coefficient of the airship, f is the fineness ratio, and vmaxis maximum relative wind speed of the airship.

Considering the aforementioned equations and parameters,the optimal design problem for a stratospheric airship can be equivalent to a multidimensional constrained nonlinear optimization problem,which can be solved using the mathematical software MATLAB.The solver fmincon is used and functions consisting of an objective function, constraint functions and linear functions, values including initial values, the lower boundary and the upper boundary, and options involving the algorithm, largescale, tolerance and so on are considered.Design variables are optimized from initial values,and random variables satisfy normal distribution. Then the optimization can be executed by the optimization toolbox.

4.3. Design results and analyses

With design variables varying continually, the optimal design solution has been obtained, and the iterative procedure of the final mass and the design variables are listed in Table 4,which gives the optimization process and demonstrates the evolution of the convergence process in 18 iterations. In the optimization process, the admissible tolerance of convergence method is ε=1×10-6. Then the total expected mass using optimal design solution is mto=518.7kg. For the sake of simplification, Table 4 only shows the results of the first several iterations and the last iteration.The result of geometry modeling after optimization can be shown in Fig.9,which is plotted through the comparison of captured shapes of the stratospheric airship. In this study, it is noticed that the structural parameters are set based on the HiSentinel80 and the value of optimal total mass is larger than the HiSentinel80. In fact,it shows that the traditional optimization method is not able to meet the reliability requirement of the stratospheric airship,and the reliability analysis should be considered based on the safety of the airship.

4.4. Sensitivity analyses

In Table 5, mass sensitivities ∂m/∂x denoting the relationship between the total mass and variables of airship are provided.With one unit increase, the corresponding increase for total mass is showcased in the last column of the form.For example,when the length of the semi-major axis of the left ellipsoid isincreased by 1 m and the remaining parameters are kept unchanged, the total mass is reduced by 4.5 kg based on the original state. It should be noted that Δm only provides the average value of the mass sensitivity because of the complicated relation of different parameters. The increase of some variables, such as a1and a2, can result in a reduction of the total mass. However, there are limits to these variables to reduce mass. This is because, though the total mass has decreased, the cylindrical center section should be lengthened to increase the volume for the increased payload mass.23As shown in Table 5, the increase in mass caused by the variable f has more increments than other variables.Therefore,in order to reduce the mass as much as possible,the variable f should be decreased with no failure.

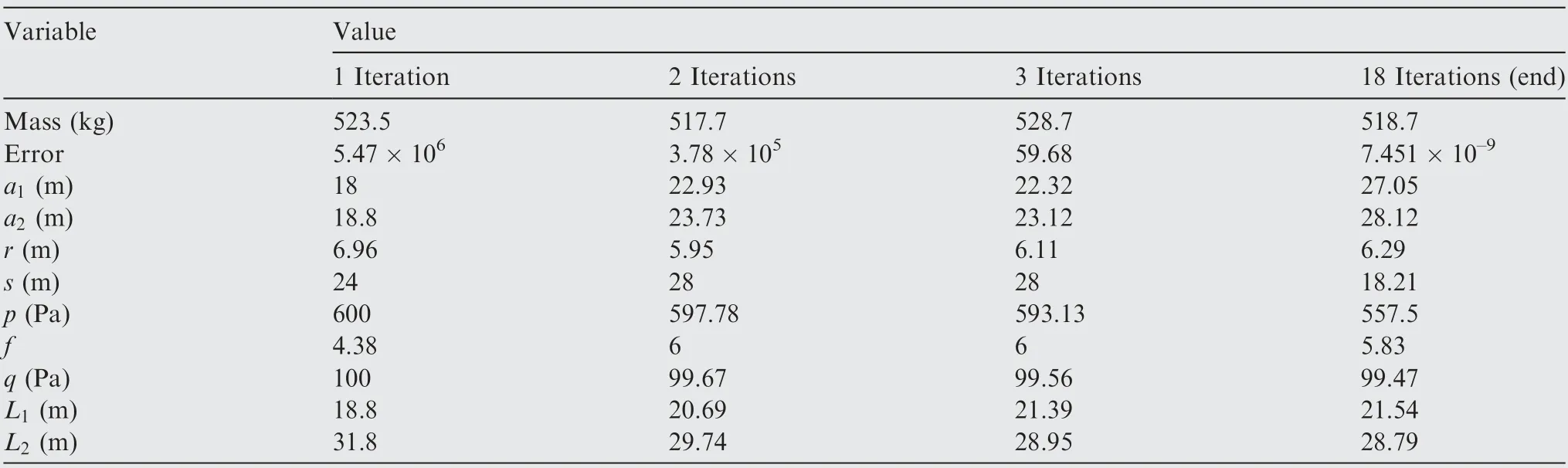
Table 4 Illustration of iterative procedure.

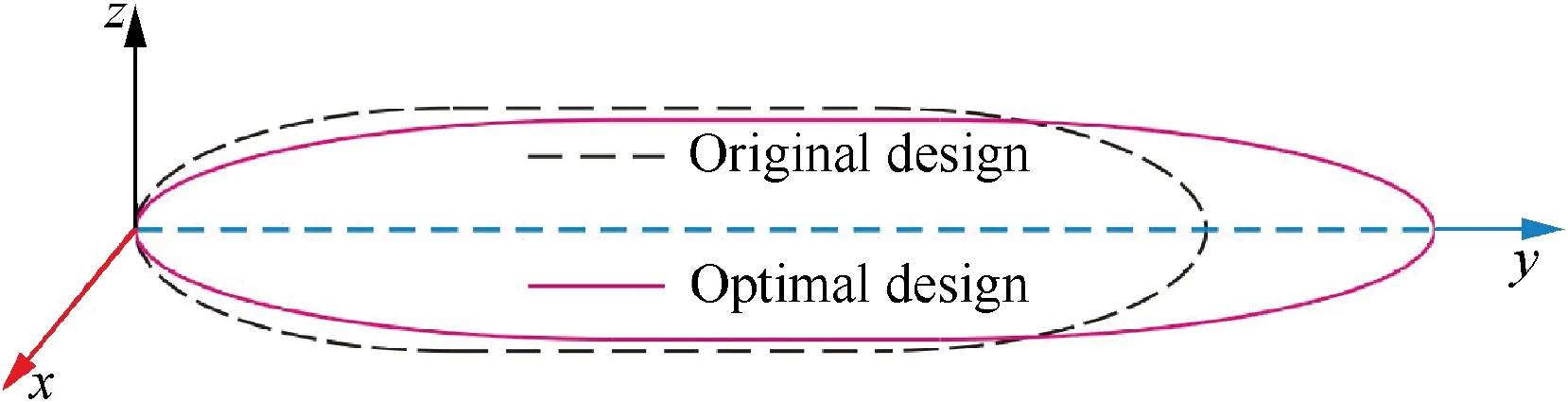
Fig. 9 Comparison of captured shapes of stratospheric airship.

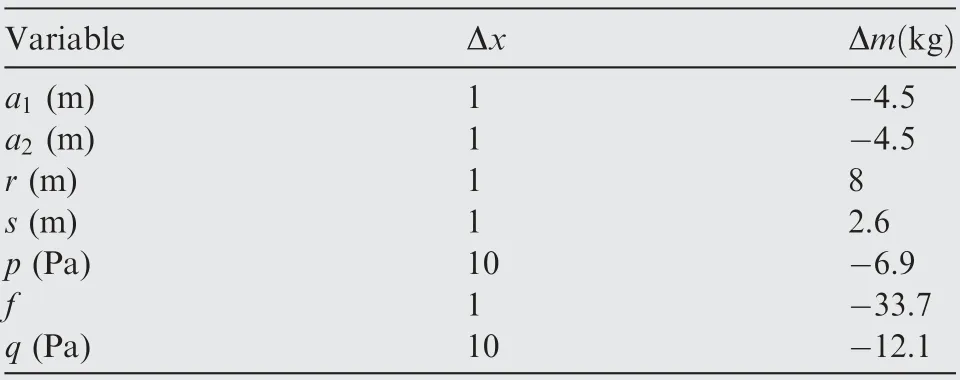
Table 5 Mass sensitivities ∂m/∂x about variables of airship.

5. Conclusions

In this paper, a complete and effective approach for the optimal design of the stratospheric airship envelope based on the reliability analysis is proposed. The ambient wind field is a significant environmental factor for the design of the stratospheric airship envelope, and the wind field based on the change of wind for the period at various altitudes is fitted.The modes of failure in this approach for stratospheric airships provide a route to illustrate the failure mechanism and calculate the total mass clearly. Then, through the establishment of multidisciplinary analysis models,the optimization solution using the optimal design approach is analyzed,interpreted and verified.

Three typical failure probabilities are given with the remaining parameters unchanged. Failure probabilities are Pw=4.7239×10-5, Ph=6.8621×10-4and Pk=4.3071×10-6, respectively. For the local uniform load, when one end is at the head or the tail of the airship and the other end is at the middle cylindrical section, the total failure probability is the highest,reaching nearly 0.006.For the wind field,the failure probability is sensitive to the scale factor c. With c=20, the failure probability reaches its maximum of 0.025.For the parameters of the airship, the failure probability reaches its minimum value when the fineness ratio is about 4.5, the differential pressure is about 400 Pa, the mean period of the wind field is reduced, and the service time of the stratospheric airship is extended.

The location,length and size of the local uniform load and the large fineness ratio are major factors to lead to bending wrinkling failure and bending kink failure. The small fineness ratio and the increasing differential pressure are more prone to cause hoop tearing failure for the airship hull.For the wind field, the failure probability is sensitive to the value of c and only a tiny change appears with the increase of k. From the example of optimization design,it is shown that the traditional optimization method cannot satisfy the reliability requirement of the stratospheric airship,and the reliability analysis must be considered based on the safety of the airship. The sensitivity analysis demonstrates that the fineness ratio f should be decreased for the reduction of the mass as much as possible without any failure.

Acknowledgements

The authors gratefully acknowledge the financial support from the National Natural Science Foundation of China (Nos.11872160 and 11572099).