Motion equations of hemispherical resonator and analysis of frequency split caused by slight mass non-uniformity

Yan HUO, Shunqing REN, Guoxing YI, Changhong WANG

Space Control and Inertial Technology Research Centre, Harbin Institute of Technology, Harbin 150080, China

KEYWORDS Hemispherical resonator;Lagrange mechanics principle;Theory of elastic thin shell;Motion equations;Mass non-uniformity;Frequency split

Abstract The mass non-uniformity of hemispherical resonator is one of reasons for frequency split, and frequency split can cause gyroscope to drift. Therefore, it is of great significance to analyze the relationship between mass non-uniformity and frequency split, which can provide a theoretical basis for mass balance of imperfect resonator.The starting point of error mechanism analysis for gyroscope is the motion equations of resonator.Firstly,based on the Kirchhoff-Love hypothesis in the elastic thin shell theory,the geometric deformation equations of resonator are deduced.Secondly,the deformation energy equation of resonator is derived according to the vibration mode and relationship between the stress and strain of hemispherical thin shell. Thirdly, the kinetic energy equation of resonator is deduced by the Coriolis theorem. Finally, the motion equations of resonator are established by the Lagrange mechanics principle. The theoretical values of precession factor and natural frequency are calculated by the motion equations, which are substantially consistent with the ones by the finite element method and practical measurement,the errors are within a reasonable range. Simultaneously, the varying trend of natural frequency with respect to the geometrical and physical parameters of resonator by the motion equations is consistent with that by the finite element analysis. The above conclusions prove the correctness and rationality of motion equations. Similarly, the motion equations of resonator with mass non-uniformity are established by the same modeling method in case of ignoring the input angular rate and damping,and the state equations with respect to the velocity and displacement of vibration system are derived, then two natural frequencies are solved by the characteristic equation.It is concluded that one of reasons for frequency split is the 4th harmonic of mass non-uniformity,and thus much attention should be paid to minimizing the 4th harmonic of mass non-uniformity in the course of mass balancing for imperfect resonator.

1. Introduction

Hemispherical Resonator Gyroscope1-4(HRG)is an all-solidstate high-precision vibratory gyro, which has the advantages of small volume,high precision,low power consumption,high reliability, short start-up time, simple mechanical structure,wide operating temperature range and strong resistance to ionizing radiation. In addition, hemispherical resonator gyro has a long service life,and the relevant data show that it can work continuously for 15 years,which is the distinct advantage over mechanical gyro, laser gyro and fiber optic gyro. In order to analyze the error mechanism of HRG, the motion equations of hemispherical resonator are established, which can be used to analyze the machining process errors,environmental-related errors, control system errors and pick-off system errors, and thus it is of extreme importance to improve the accuracy of gyroscope. Zhuravlev5introduced the fundamental principle of resonator gyros using Foucault pendulum model. Saunders and Paslay6analyzed the inextensional vibration of a spherecone shell and compared the theoretical calculation value with the experimental value of natural frequency. Chang et al.7investigated the precession of standing wave in the hemispherical shell and considered the influence of Coriolis force and centrifugal force on the precession of standing wave, and the conclusion that centrifugal force affects the natural frequency of standing wave while it does not affect the precession factor was drawn. Wang et al.8established a temperature compensation model by the natural frequency of resonator and made compensation for the temperature drift of gyroscope.The generalized Coriolis Vibration Gyroscope motion equations deduced by Lynch,9in which the misalignment of inherent frequency axis and inherent damping axis were taken into account, are the most widely used motion equations included in IEEE Standards.10Ref. 11 deduced the motion equations of hemispherical resonator by the Bubnov-Galerkin method.However, the natural frequency obtained by this model is severely distorted due to the errors in the derivation process.Zhao et al.12rederived the equations of motion of hemispherical resonator and corrected the errors,and then the theoretical value of natural frequency of resonator is consistent with the measured one on the order of magnitude, but the error is still very large.The modeling method introduced in Ref.13 is basically the same as that in Ref. 11. The differences are that the motion differential equations of hemispherical resonator are not limited to the lip edge, but the whole resonator, and the strains in the mid-surface of resonator are neglected.However,the calculated natural frequency is always 0,which indicates a fundamental flaw in modeling method. Wang et al.14established the dynamic model of procession of standing wave of hemispherical resonator based on the virtual work theorem.However,the theoretical values of precession factor and natural frequency do not match the measured results. Li15simplified the hemispherical thin shell into a thin elastic ring, and the motion equations of resonator were obtained by the Bubnov-Galerkin method. However, the theoretical value of precession factor is seriously inconsistent with the measured one.15Yu et al.16analyzed the natural frequency of hemispherical resonator under the second-order vibration mode by the finite element method, and compared them with the measured results, which proved the correctness of modal analysis. Loveday and Rogers17demonstrated the ability of control system to suppress the effects of the first order of resonator with frequency imperfections.Choi and Kim.18proposed that the perturbation of point masses on the hemispherical resonator can be expressed by functions for the drift angle of mode orientation and frequency split based on the Rayleigh’s energy method, and the model with multiple point masses can be expressed as the model with an equivalent single point mass.Shatalov et al.19analyzed the evolution of standing wave in a mass-unbalanced sphere. The conclusion is that the precession angular rate is affected by the external input amplitude and the orthogonal mode, and if the orthogonal term is not suppressed, the ‘‘capture effect” of standing wave appears to occur. Fox20established the model of circular ring with small attached masses and springs by the Rayleigh-Ritz method and introduced the conception of an equivalent imperfection mass.Bisegna and Garuso21presented the expression of trimming mass and applied the frequency trimming of an imperfect ring.Lin et al.22investigated an axisymmetric multi-curved surface resonator and proposed an approach to eliminate frequency split. Basarab et al.23applied electrochemical etching procedure in balancing the 1st-4th harmonics of mass nonuniformity of cylindrical metal resonator.Wang et al.24experimentally investigated the use of a chemical etching procedure to decrease the frequency split of hemispherical resonator made of fused quartz.These studies are of very important theoretical significance and engineering value, which provide a theoretical basis for the dynamic model of hemispherical resonator.

In this paper,the motion equations of resonator are derived by applying Lagrange mechanics principle and theory of elastic thin shell, and the theoretical values of precession factor and natural frequency are more accurate than those of previous works.Based on the same modeling method,the motion equations of resonator with mass non-uniformity are deduced.Furthermore, the state equations regarding velocity and displacement of vibration system are established. Finally, the frequency split is determined by the eigenvalues of state equations.It can be found that the frequency split is mainly caused by the 4th harmonic of mass non-uniformity, and the key to mass balance of imperfect resonator is to remove the 4th harmonic of mass non-uniformity.

2. Working principle of hemispherical resonator

HRG is a device that senses an angular velocity of pedestal by detecting the variation of standing wave of resonator.The geometric profile of resonator is shown in Fig. 1, the geometric and physical parameters are shown in Table 1. The standing wave of resonator under the second-order vibration mode is in the form of four-antinode. When the lip edge of resonator is deformed to the maximum, the major axes and the four intersections of two ellipses are called the antinode axes and the nodes, respectively, as shown in Fig. 2(a). When the sensitive axis of resonator is exerted an input angular rate, the standing wave will precess relative to its initial position on the hemispherical thin shell, as shown in Fig. 2(b), where ϑ is called the azimuth of antinode. The primary oscillation of resonator is the second-order vibration mode, the relationship between Ω and ϑ is as follows:

where K is defined as the precession factor of resonator.

3. Motion equations of ideal hemispherical resonator

3.1. Establishment of coordinate systems

The geometry deformation and shell stress of mid-surface of resonator are shown in Fig.3.Moreover,the established coordinate systems are also illustrated in Fig. 3, respectively.

Orthogonal Curvilinear Coordinate System P-αβz:Origin P is located on the mid-surface of resonator,axis z is the normal direction of mid-surface,axes α and β are the tangent lines of the longitude(generatrix)and latitude(ring)circles located on the mid-surface,and axes α,β and z are mutually orthogonal.

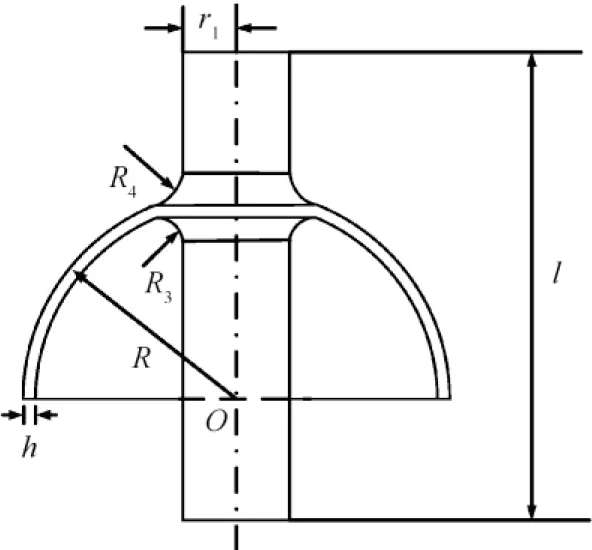
Fig 1 Sectional view of hemispherical resonator.

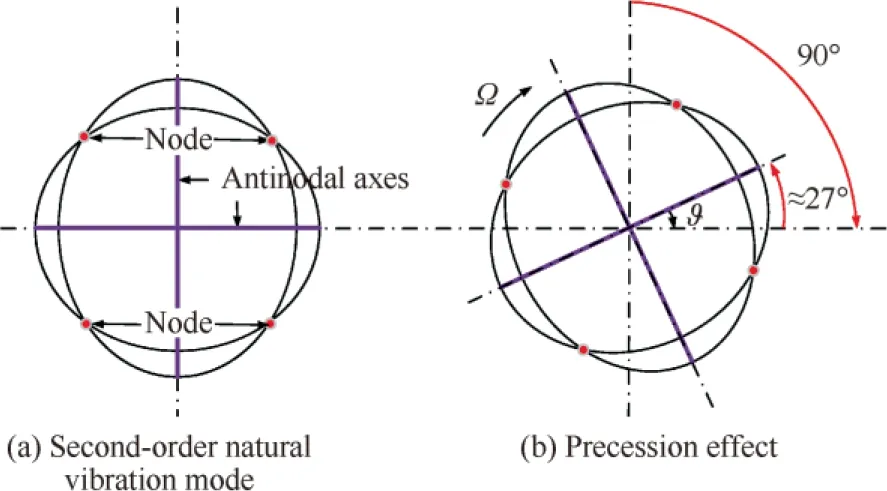
Fig 2 Precession principle of hemispherical resonator.

Hemispherical Resonator Coordinate System O-xhyhzh:Origin O is at the center of ground opening of resonator.Axiszhis coincident with the symmetry axis of resonator.Axesxhandyhare on the ground plane of resonator and are perpendicular to each other.

Local Coordinate System P-e1e2m:Origin P is located on the mid-surface of resonator, and axes e1,e2andm are parallel to the tangential direction of coordinate curves α, β and z,respectively.

3.2. Geometric parameters of mid-surface of hemispherical resonator

When the resonator works in the second-order state, a point of mid-surface of resonator moves from position P to position P′. The vector S in the local coordinate system P-e1e2m is expressed by

Table 1 Geometric and physical parameters of resonator made of fused quartz.

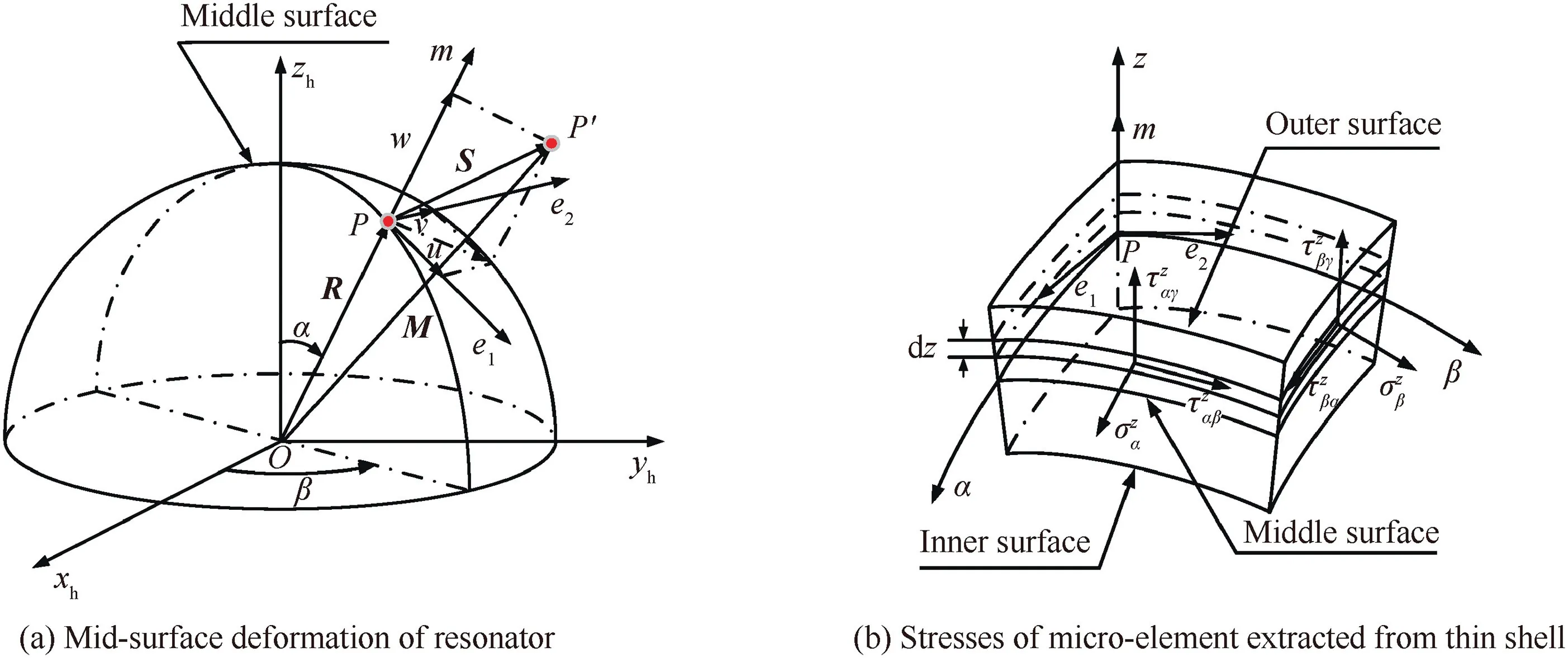
Fig 3 Coordinate system and model of hemispherical resonator.

where u, v and w are the components of displacement PP′in directions e1, e2and m, respectively.

The relationship between the vectors M and R is written as

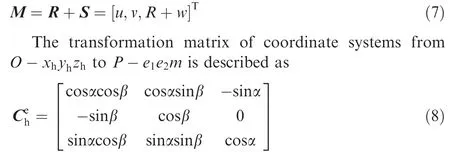
3.3. Deformation energy of hemispherical resonator

The geometric deformation equations25of mid-surface of thin shell are expressed as

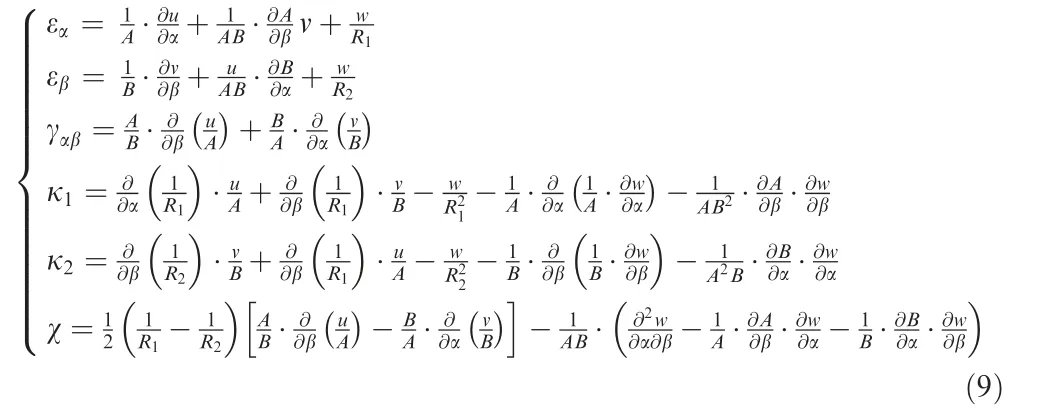
where εαand εβare the normal strains of mid-surface in directions α and β,respectively;γαβis the shear strain of mid-surface on the plane determined by the coordinate tangential lines α and β; κ1and κ2are the principal curvatures of mid-surface in directions α and β, respectively; χ is the twist rate of midsurface.

Substituting Eqs. (3) and (4) into Eq. (9), yields

Based on the theory of elastic thin shell,25the strains on a point with the distance z from the mid-surface of resonator are given by

The first integral of Eq. (14) only contains εα, εβand γαβ,which correspond to the deformation energy of membrane stress. The second integral only contains κ1, κ2and χ, which correspond to the bending and torsion deformation energy.The vibration amplitude of resonator under the secondorder vibration mode is in the order of micrometers, the assumption that the mid-surface is not stretchable27can be applied, then

Substituting Eqs. (4) and (15) into Eq. (14), the approximate deformation energy of resonator is rewritten as

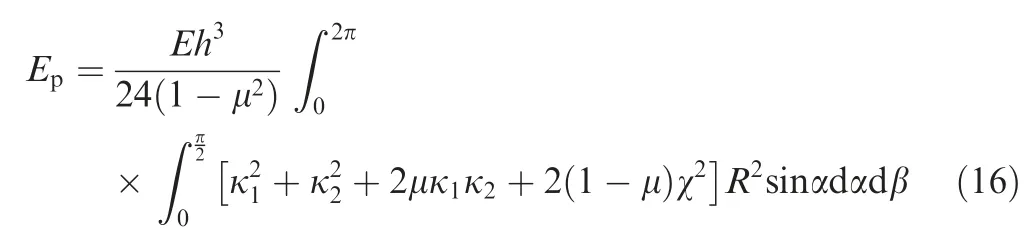
3.4. Second-order vibration mode function

Assuming that the resonator works in the second-order vibration mode,11the displacement components of a point on the mid-surface of resonator are expressed by

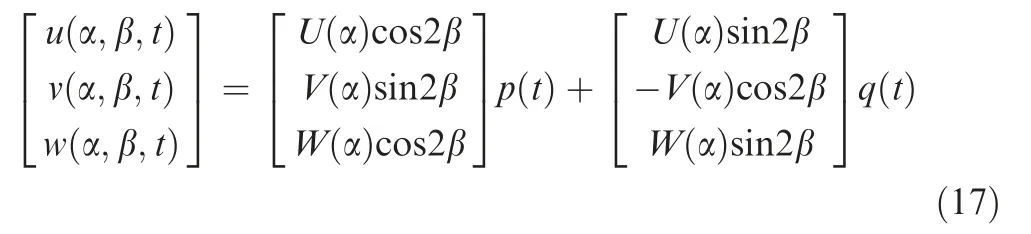
where U(α), V(α) and W(α) are Raleigh’s functions, which restrict the displacement relationship among different microelements of resonator. p(t) and q(t) are time-dependent harmonic oscillation functions to reveal the amplitude, frequency and phase information of vibration system, and their directions are shown in Fig. 4.

Substituting Eq.(17)into Eqs.(10)and(15),the differential equations related to Raleigh’s functions are given by

The central attention is paid to the form of Raleigh’s functions rather than their amplitudes, then C1=1 can be considered.

3.5. Kinetic energy of hemispherical resonator

The input angular rate of resonator is expressed by

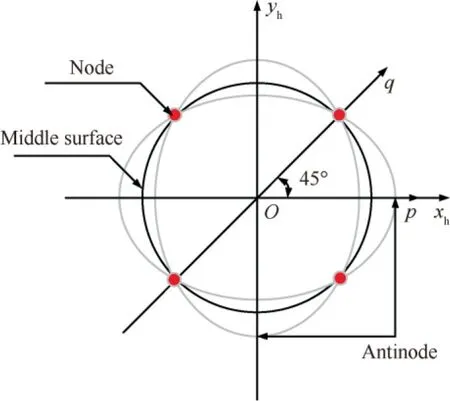
Fig 4 Mechanical model of ideal resonator.

where ρ is the density of resonator, if the density is uniformly distributed along the circumference of resonator,it can be considered that ρ=ρ0.

3.6. Motion equations of hemispherical resonator

It is known from the orthogonality of trigonometric function system that, for integers m and n,

3.7. Natural frequency and precession factor of hemispherical resonator

Neglecting Ω2, ˙Ω and ω0/Qf, the complex variable Z=p(t)+q(t)j is introduced to represent the trajectory of standing wave,where j is an imaginary unit.

Eq. (35) is represented by

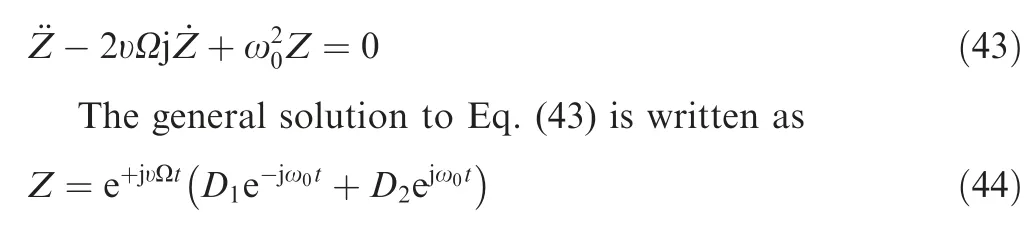
where D1and D2represent the values determined by the initial vibration condition.

Eq. (44) shows that the vector diameter of Z point on the complex plane rotates at the angular rate υΩ . Therefore, the standing wave rotates at the angular rate υΩ/2 on the body of resonator.

The azimuth of standing wave of resonator is obtained by

The equivalent mechanical model of ideal resonator is shown in Fig. 5.

3.8. Simulation and measurement of natural frequency and precession factor

The finite element method is used to analyze the vibration mode and natural frequency of resonator, as shown in Fig.6.The closeness between the theoretical and measured values for precession factor and natural frequency can reflect the accuracy of motion equations

The relative error is defined as

where fmrepresents the measured or simulated value of natural frequency.

The geometric and physical parameters of resonator are displayed in Table 1,and the theoretical and simulation values of natural frequency are shown in Tables 2. Moreover, the measured values of natural frequency are given in Table 3,which contains the measured natural frequencies of three different batches of resonator in Ref.16. In addition, the measured value of precession factor are shown in Table 4, which is provided by Refs. 11. Tables 2 and 3 show that the motion equations of resonator in Refs. 11-13 are severely distorted regarding the natural frequency, Table 4 indicates that the motion equations of resonator in Refs. 15,16 are severely distorted regarding the precession factor.

The investigation of influence of geometric and physical parameters on the natural frequency can be helpful to the materical selection and structure design of resonator. Therefore,the varying trend of natural frequency(f)needs to be analyzed when the geometry and physical parameters vary. As shown in Fig. 7(a)-(h), it can be found that the motion equations in this paper is more reasonable. In comparison, the motion equations in Ref. 12 has the serious problem because the varying trend of natural frequency by the motion equations is completely opposite to that of finite element simulation when the Poisson’s ratio and thickness vary independently.Moreover,themotion equations in Ref.13 also has the serious problem because the theoretical value of natural frequency is always 0. In addition, the natural frequencies for different ratios of radius to thickness (R/h) are investigated. Fig. 7(f)reveals that the natural frequency decreases with the increase of ratio of radius to thickness,and the influence of radius variation on the natural frequency seems to be more effective than that of thickness variation. In particular, it should be pointed out that the influence of inner and outer corner radius of resonator on the natural frequency cannot be reflected by themodeling method in this paper, but it can be analyzed by the finite element simulation. As shown in Fig. 7(g) and (h), the influence of inner corner radius on the natural frequency is much greater than that of outer corner radius,and the natural frequency increases with the increase of inner and outer corner radius, which can be approximated as a linear relationship within a certain range.

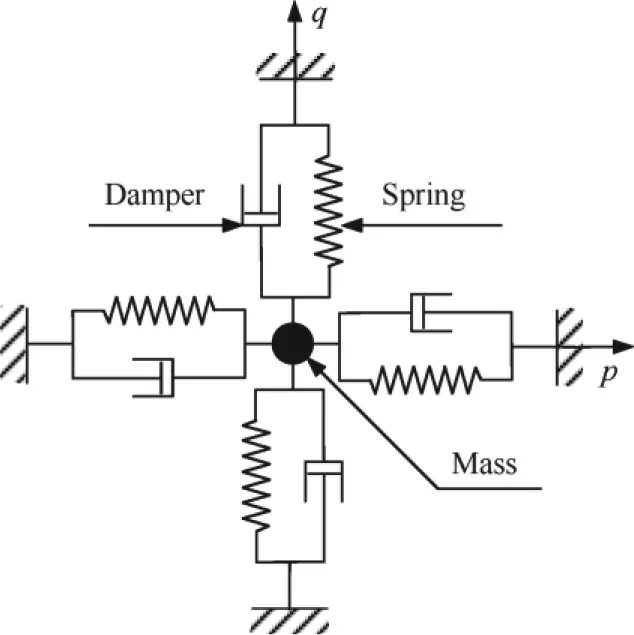
Fig 5 Equivalent mechanical model of ideal resonator.

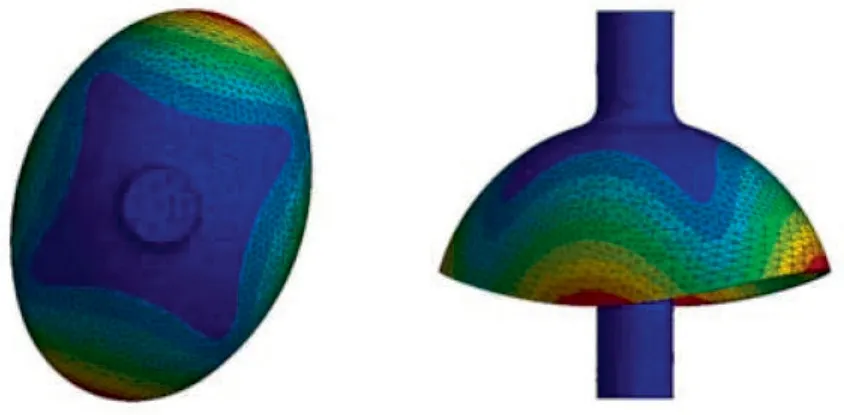
Fig 6 Finite element simulation of second-order vibration mode of hemispherical resonator.

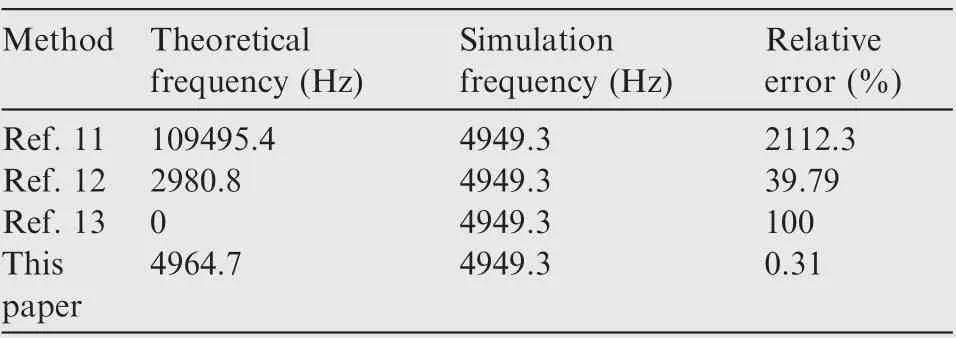
Table 2 Comparison of natural frequencies obtained by motion equations and finite element method.

Table 3 Comparison of natural frequencies obtained by motion equations and measured data.

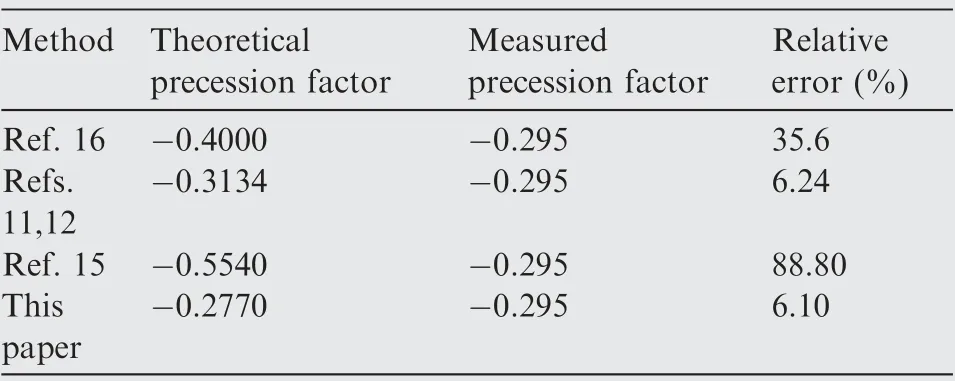
Table 4 Comparison of precession factors obtained by motion equations and measured data.

4. Frequency split caused by mass non-uniformity of hemispherical resonator

4.1.Motion equations of hemispherical resonator with mass nonuniformity

One of main error sources in HRG arises from the mismatch in natural frequencies of two principal vibration modes.9The difference between two natural frequencies is defined as frequency split, which is given by

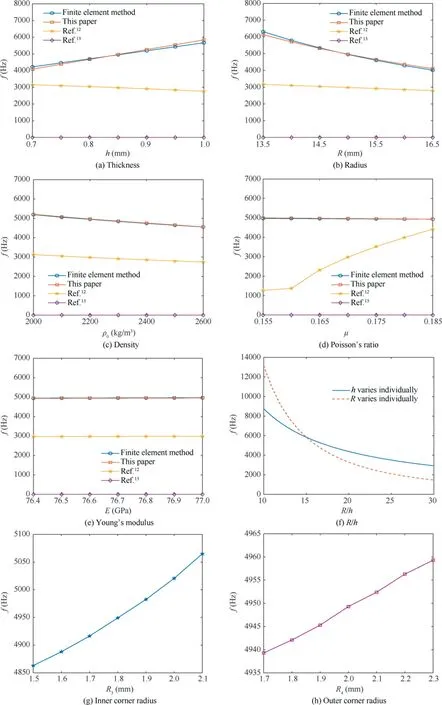
Fig 7 Natural frequency curves varying with parameters of hemispherical resonator.

4.2. State equations ofdisplacement and velocity of vibration system

Eq.(63)reveals the relationship between the relative amplitude of the 4th harmonic of mass non-uniformity and frequency split, as shown in Fig. 8.

Eq. (67) shows the motion equations of a two-dimensional mass-spring system in which there are two inherent rigid axes pωand qωalong which the natural frequencies of system are slightly different, as shown in Fig. 9. Correspondingly, two inherent rigid axes pωand qωare separated by interval 45°on the resonator body, as shown in Fig. 10.

Fig 8 Relationship between relative amplitude of the 4th harmonic of mass non-uniformity and frequency split.

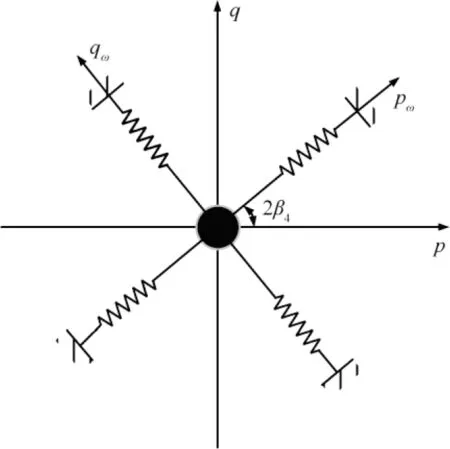
Fig 9 Equivalent mechanical model of imperfect resonator.

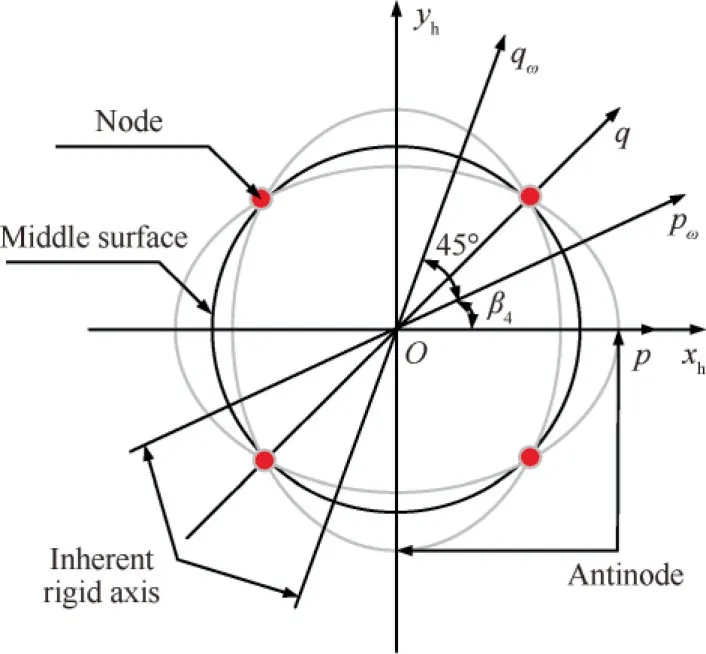
Fig 10 Mechanical model of imperfect resonator.

5. Conclusions

(1) The motion equations of perfect hemispherical resonator are established by Lagrange mechanics principle and theory of elastic thin shell.The theoretical values of precession factor and natural frequency are basically consistent with the simulated and measured values,which proves the correctness and rationality of motion equations.

(2) By the same modeling method, the motion equations of hemispherical resonator with mass non-uniformity are established in the case of ignoring the damping and input angular rate, and the state equations of displacement and velocity of vibration system are derived.Two second-order natural frequencies are solved by the characteristic equation.

(3) The 4th harmonic of mass non-uniformity of hemispherical resonator is one of reasons for frequency split,which indicates that much attention should be paid to minimizing the 4th harmonic of mass non-uniformity for mechanical balancing of imperfect resonator.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

This study was supported by the Pre-Research Fund during the ‘‘13th Five-Year Plan” (No. 41417060101).