Optimization of bits allocation and path planning with trajectory constraint in UAV-enabled mobile edge computing system

Yizhe LUO, Wenrui DING, Bochng ZHANG, Wenqin HUANG,Chunhui LIU

a School of Electronics and Information Engineering, Beihang University, Beijing 100083, China

b Institute of Unmanned System, Beihang University, Beijing 100083, China

c School of Automation Science and Electrical Engineering, Beihang University, Beijing 100083, China

KEYWORDS Constraint implementation;Edge computing;Energy consumption;Optimization methodology;Unmanned Aerial Vehicles(UAV)

Abstract In this paper, an Unmanned Aerial Vehicle (UAV) enabled Mobile Edge Computing(MEC) system is studied, in which UAV acts as server to offer computing offloading service to the Mobile Users(MUs)with limited computing capability and energy budget.We aim to minimize the total energy consumption of MUs by jointly optimizing the bit allocation for uplink,computing at the UAV and downlink, along with the UAV trajectory in a unified framework. To this end, a trajectory constraint model is employed to avoid sudden changes of velocity and acceleration during flying.Due to high-order information in use,we lead to a more reasonable nonconvex optimization problem than prior arts. An Alternating Direction Method of Multipliers (ADMM) method is introduced to solve the optimization problem, which is decomposed into a set of easy subproblems, to meet the requirement on the efficiency in edge computing. Numerical results demonstrate that our approach leads a smoother UAV trajectory, significantly save the energy consumption for UAV during flying.

1. Introduction

Nowadays, Mobile Edge Computing (MEC) has attracted much attention,1-6since it can help the users with limited computation capability handling computation-intensive latencycritical tasks, which is regarded as a promising way toward the future communication. With a high mobility, Unmanned Aerial Vehicles (UAV) have been widely used in the wireless communication.7-16The UAV-enabled MEC system is a new attempt in civil and military fields, especially in the extreme environment i.e., disaster area, battlefield or remote area,where the base stations and MEC servers are lack. In this situation, UAV can act as an aerial base station or MEC server for its easy deployment and flexible movement.By jointly optimizing the computation resource allocation,the power control and UAV trajectory can improve the QoS(Quality of Service)of a MEC system and decrease the energy consumption.

In Ref. 17,18, a mobile cloud computing system was built based on a UAV-mounted cloudlet, in which UAV acted as a cloud server with limited computing capability to provide a task offloading service to ground Mobile Users (MUs). UAV flied in a fixed trajectory, researchers minimized the sum of the energy of MUs by optimizing the bit allocation for uplink,computing at UAV and downlink,17and the UAV trajectory is only analyzed with the bit allocation jointly, but not considered in the optimization. Besides, a non-orthogonal access scheme for uplink and a UAV energy consumption model were proposed based on the acceleration,18actually the secondorder information.The problem was tackled based on Successive Convex Approximation (SCA) under two access schemes and two UAV energy consumption models respectively. In Ref. 19, UAVs acted as mobile users and can send tasks to the ground base station for further computing, which take place by means of time division duplex. The researchers minimized the total task processing time subject to the comprehensive constraints from the UAV velocity, initial and final position, as well as ground base station processing capability.An alternative algorithm was proposed to get a high-quality suboptimal solution. An UAV- enabled mobile edge computing system was proposed with the UAV as MEC processor as well as relay between ground User Equipment (UEs) and MEC server in Ref. 20. The optimization was solved by minimizing the weighted sum energy consumption of UAU and UEs under task-driven constraints, information-causality,bandwidth allocation and the UAV’s trajectory constraints.MEC and Wireless Power Transfer (WPT) techniques were combined together in Ref.21,in a given scenario,UAV served as the MEC processor and wireless power transfer transmitter to provide power and MEC service under partial offloading mode to users. The goal of minimizing the UAV energy consumption subject to the constraints of computation bits and energy harvesting causality, was achieved by an alternative algorithm based on sequential convex optimization. On the basis of Ref. 21, a computation rate maximization problem was investigated in Ref. 22, the CPU frequency of UAV,offloading duration, transmit power of users, as well as the UAV trajectory was optimized by a three-stage alternative algorithm. The work was completed under both binary offloading mode and partial offloading mode.

In Ref.23-25,the MEC system was built based on multiple UAVs. A game theory model was adopted in Ref. 23, which minimized the energy consumption by finding the Nash equilibrium of the cost function. In Ref. 24,the MEC system with cellular-connected UAV was proposed by considering four access schemes in the uplink transmission, i.e., Time Division Multiple Access (TDMA), Orthogonal Frequency Division Multiple Access (OFDMA), One-by-One access and Non-Orthogonal Multiple Access (NOMA), to minimize the total UAV energy consumption by SCA under four access schemes respectively. Differently in Ref. 25, researchers considered the UAV altitude in the sum power minimization, to optimize the user association, power control, computation capacity allocation and location planning by SCA and Fuzzy C-Means(FCM) respectively.

However, previous works on UAV energy consumption model only consider the constraint on the velocity, acceleration into the optimization, at most the second-order information. We consider a long-run strategy to further improve the flying to save the energy by avoiding sudden change of velocity and acceleration,which is more practical for real applications.We introduce the trajectory constraint as an extra backbone,which can be efficiently solved based on the ADMM method.

The main contributions of this paper are summarized as follows:

(1) A trajectory constraint is introduced into the UAV energy consumption model, as a penalty term to the optimization objective function. The penalty term value is defined as a ratio of the Euclidean distance and the Geodesic distance of UAV at different time slots. The trajectory constraint guarantee that UAV cannot change both the velocity and acceleration suddenly,thus leading to a smoother trajectory, which benefits a real UAV flying.

(2) The advantages of our method also come from its optimization to a complex non-convex problem, based on the ADMM approach. To solve it,the original problem is decomposed into four sub-problems, while each subproblem can be solved by existing non-linear convex programming method, and thus the original problem can be efficiently solved by addressing four subproblems iteratively.

(3) Numerical results show that the optimized UAV trajectory is smoother and avoid the velocity and acceleration sudden change. The UAV flying energy consumption is saved based on the smooth trajectory, consequently the UAV service time will increase, because the saved energy is much more than the energy increasing.

2. The methodology

As shown in Fig.1,a MEC system is considered,which consist of one UAV MEC server,K ground users.The UAV equipped with a single antenna and a power limited processor. The system can be used for search and rescue mission based on the collaboration of UAV and robots, where UAV provides the environment information for the robots to implement the necessary operations. In this way, the heterogeneous devices can work together to finish the mission more efficiently. We use the same system model and optimization problem in Ref.17,18, based on which we considered the trajectory constraint for a further study.

2.1. Basic model

The optimization is to minimize the total energy consumption of every user k, k ∈K=｛1，2，...，K｝, with the constraint that all the users’ data to be processed within the time T. And T is divided into N slots, and the duration of each time slot is Δ. At one time slot, in order to avoid interference between users,the time division multiple access scheme is adopted,each user has Δ/K to communicate with UAV. For the uplink and downlink channel, a Frequency Division Duplex (FDD) is adopted, where each channel is allocated with bandwidth B.

where γ is the effective switched capacitance of UAV,and C is the number of CPU cycles per input bit of the data to be processed. Downloading energy consumption for the user k is same as Eq. (1):

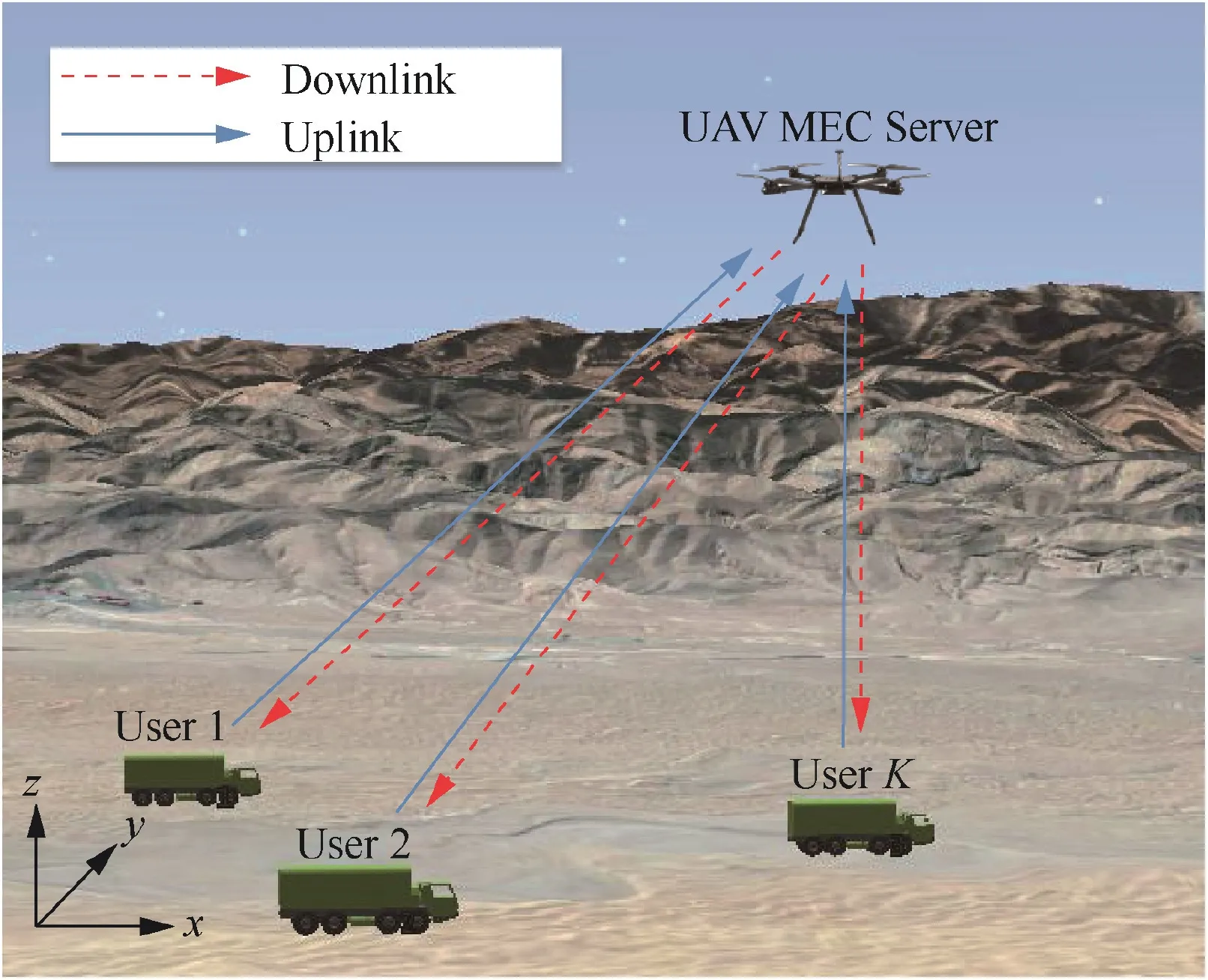
Fig. 1 Mobile edge computing scenario.

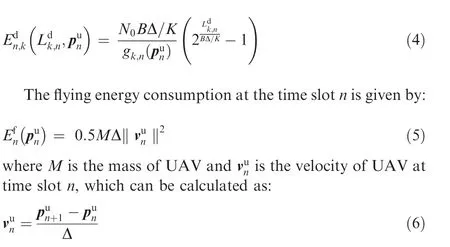
2.2. Trajectory constraint

Based on the model mentioned above, we introduce a trajectory constraint into optimization. As shown in Fig. 2, in the real situation,to make the flight more stable,UAV will choose a smooth trajectory.In other words,changing the direction of flight should avoid the sudden change of the velocity and acceleration. Most previous works concentrated on the constraint of UAV velocity and acceleration.Two neighboring time slots UAV position is needed during UAV velocity calculation, as for UAV acceleration calculation,the number of needed neighboring time slots comes to three, which means most previous works impose the constraint on the position of only three neighboring time slots. We consider that the position at time slot n is related with the former Q positions and impose a constraint on the UAV position of Q neighboring time slots to get a smoother and more realistic trajectory.

In addition,the existing UAV distance calculation between two time slots is based on Euclidean distance DE.However,in real applications, UAV does not fly over a plane but a cambered surface, as shown in Fig. 3, when UAV flies on a fixed altitude,the trajectory of UAV is also an arc but not a straight line. Therefore, the true distance between two time slots UAV position is the geodesic distance DG,which is given for the time slot n and n-1 as:

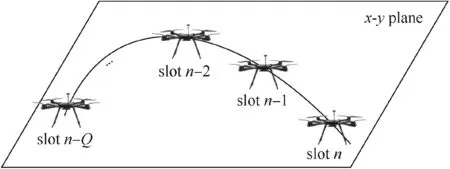
Fig. 2 UAV flies with trajectory constraint.

Fig. 3 Euclidean distance and geodesic distance.

where β is a constant less than 1,standing for the relevance of the slot n and slot n-i, as i grows, the relevance between two time slot is decrease.Q is the number of neighboring time slots we concerned about, which means the UAV position in time slot n is relative with the former Q time slots position. In this paper, Q is set to be 5.Especially, when n is from 1 to 5, Pnis formulated as:

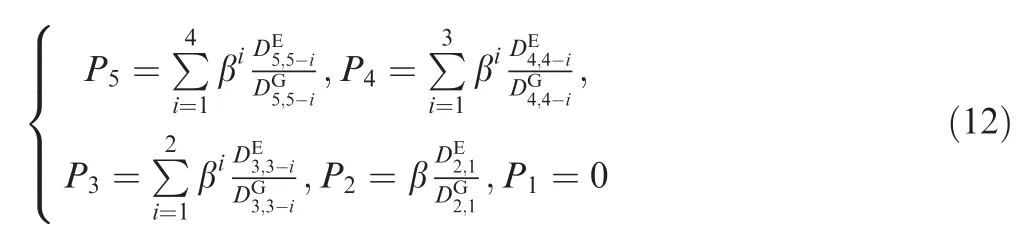
3. Optimization by ADMM

Successive Convex Approximation(SCA)is widely used in the previous works,which relaxes a nonconvex optimization problem as an approximate convex problem.26-27However,SCA is inefficient because of a large amount of optimized variables.As such, we introduce an Alternating Direction Method of Multipliers (ADMM) method to resolve the optimization problem with separability,which is featured with fast processing speed and good convergence performance. It decomposed a complex problem into several simpler sub-problems to reduce the optimization scale, hence the original optimization can be solved by optimize the sub-problems alternatively. In the proposed ADMM method, the optimal variables consists of uploading data bits,processing data bits,downloading data bits and UAV path. To reduce the computational complexity,we consider decomposing our presented optimization into four sub-problems and optimizing their variables individually. The ADMM method has two advantages in our optimization problem:

(1) The amount of the optimal variables is reduced by three quarters,thus decreasing the computational complexity.

(2) When dealing with the variables of one sub-module,those of other sub-modules are regard as constant,which makes the sub-problems convex to obtain better optimal results.Besides,the added penalty term can also be easily solved in the ADMM framework without the additional burden involved for the optimization.

3.1. Problem formulation

where the penalty term of trajectory constraint Pnis defined in Eqs.(11)and(12),E in Eq.(13b)is the total UAV energy budget.Eq.(13c)guarantees that the bit number of processed data in UAV is no more than the one UAV received.Eq.(13d)aims at the bits number of the downloading data is no more than the bits number of the processed data, and Okis the output data bits per input data bits processed in UAV of user k.Eqs.(13e)-(13g)instead means that data of each user has been processed before the end time, Ikis the total data bits number of user k,and Eq.(13i)is the terminal constraint of UAV position,which means UAV must take off from puIand land on puF.

3.2. Alternating direction method of multipliers

?

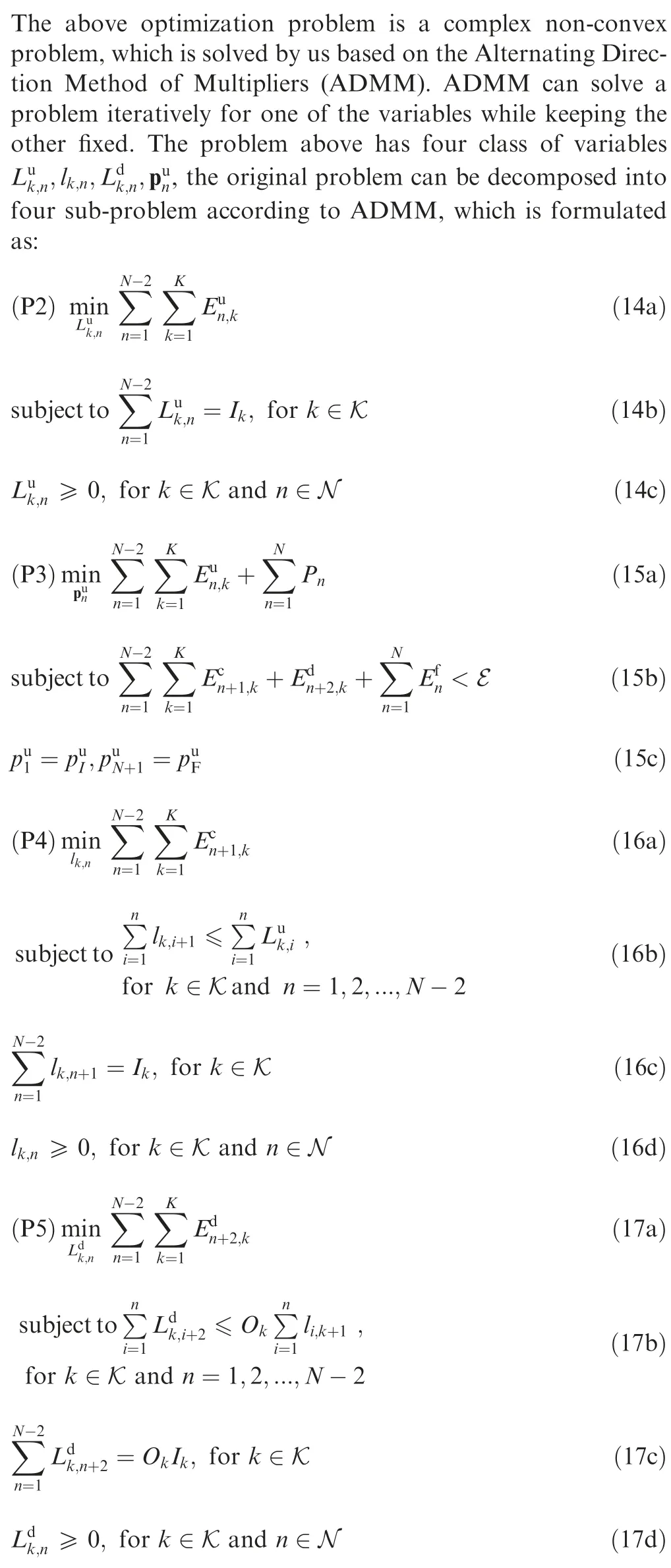
For (P4), the objective function is nonconvex, however, the function is a square term of a sum function, a local optimal solution can still be found based on a convex method.Besides,the objective function of(P4)is a constraint term in Eq.(13b),if the final solution of(P1)satisfies constraint Eq.(13b),a local optimal solution of (P4) is acceptable.

For (P5), the formula of the objective function is same as(P2), which can be solved in the same way.

Given an initial feasible solution, an iterative algorithm is proposed to solve the original problem by optimizing the four variables iteratively. The whole algorithm is described in Algorithm 2.

Algorithm 2 Iterative algorithm to (P1)1. Given a feasible initial solution Luk，n（0），lk，n（0），Ldk，n（0），pun（0）2. Set j=0 3. Calculated the original objective function value Obj (j) using Luk，n（j），lk，n（j），Ldk，n（j），pun（j）4. Get Luk，n（j+1） by solving (P2) with fixed lk，n（j），Ldk，n（j），pun（j）5. Get pun（j+1） by solving (P3) with fixed Luk，n（j+1），lk，n（j），Ldk，n（j）6. Get lk，n（j+1） by solving (P4) with fixed Luk，n（j+1），Ldk，n（j），pun（j+1）7. Get Ldk，n（j+1） by solving (P5) with fixed Luk，n（j+1），lk，n（j+1），pun（j+1）8. Calculated the original objective function value Obj (j+1)using Luk，n（j+1），lk，n（j+1）， Ldk，n（j+1），pun（j+1）9. if Obj（j + 1）-Obj（j）|≤ε|10. Output the final solution Lu k，n（j+1），lk，n（j+1），Ldk，n（j+1），pun（j+1）11. Stop the algorithm 12. else 13. j+1 →j, go to 4 14. end if

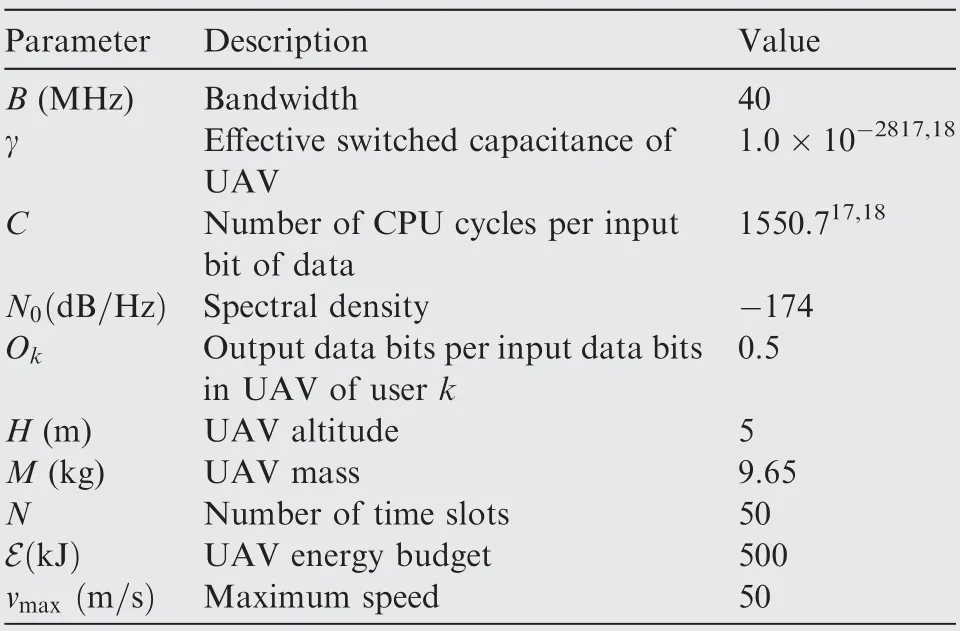
Table 1 Parameters setting.

4. Numerical results

In this section, the numerical simulations are presented, the related parameters are shown in Table 1. To compare with the result in Ref. 18, we use the same parameters detailed in the reference paper.

In the first scenario, we compare the optimization results using ADMM with the published results.18User 1 and user 2 is uniformly distributed in a 10×10 m2area with both 8 Mbits data.We assume that the position of users are(10,0)and(0,10)respectively, the initial and the final position of UAV are(0,0)and (0,8), the reference SNR g0/N0B is -2.5 dB.

To indicate the effectiveness of the proposed ADMM, we compared it with the Successive Convex Approximation(SCA) approach, which is used in the same scenario in Ref.18.As shown in Fig.4,the total user energy consumption optimized by ADMM with and without the proposed constraint are both less than that optimized by SCA, especially when the deadline T is small. It means that our proposed method achieves a better performance in emergency. The result without constraint shows a minimum energy consumption. In Fig. 5, it shows that without constraint, UAV moves to the users directly and when users start uploading the data, UAV is right above the users and then get the minimum path loss.Corresponding optimized data bits are shown in Figs. 6 and 7. It shows that users choose to upload data when nearest to UAV, and that consumes the minimum energy.

However, the trajectory with proposed constraint is smoother and avoid sudden change of velocity,UAV can have a less energy consumption under smooth trajectory, shown in Fig. 8. Although users will consume more 2-7 J energy under trajectory constraint, but it saved at least 1000 J energy of UAV, which will increase UAV service period.

In order to far more test the UAV energy saving characteristic of the proposed trajectory constraints, we compare optimization result with/without the constraints in different conditions,in terms of different energy budget,users’position and data bit number. The conditions setting are shown in Table 2. Besides, the initial and the final position of UAV is(0,0) and (0,5), the reference SNR g0/N0B is -5 dB and the other parameters keep same value in Table 1.

Comparing the optimized results from Condition (1) to Condition (4), we analyze the impact of UAV energy budget which is shown in Figs. 9-12.

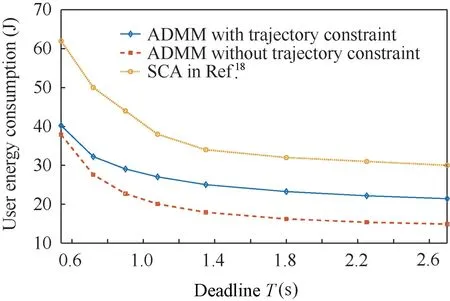
Fig. 4 Optimized user energy consumption by ADMM and SCA.

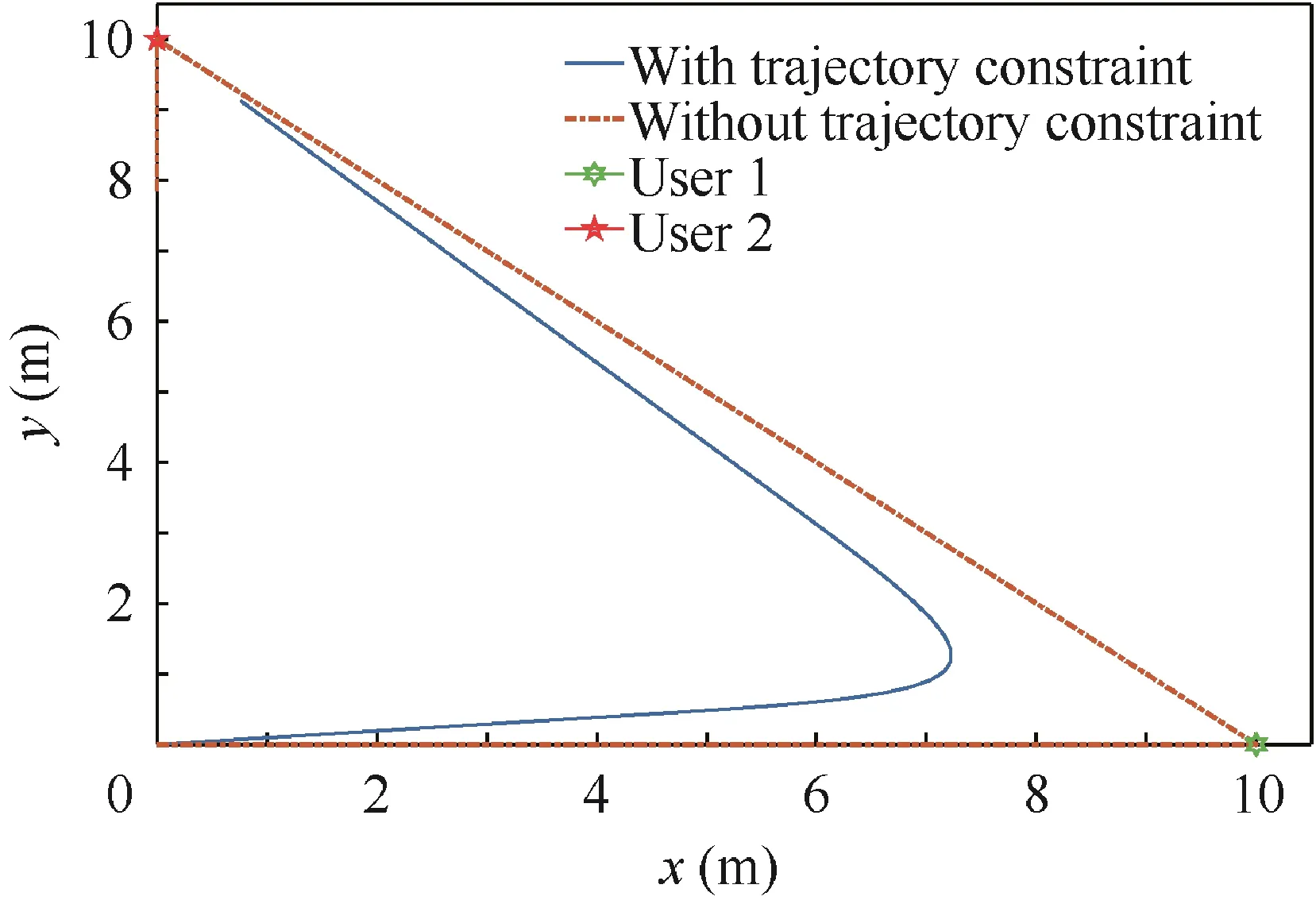
Fig. 5 Optimized trajectory with and without proposed constraint.

In the Condition (1), UAV energy budget can not support the flying consumption to cover all users,while UAV flies over each user instead of stay above the users,leading to more user energy consumption. Form condition (2) to condition (4),UAV energy budget is enough, UAV can cover all users and the user energy consumption is less. Besides, the result form Condition(2)to Condition(4)keep same for the UAV energy consumption is all under budget in different conditions.

Comparing the optimized results from Condition (5) to Condition (8), we analyze the impact of the user position which is shown in Figs. 13-16.

As the users distribution get closer,UAV’s flying trajectory get shorter,and the distance between users and UAV get smaller, the energy consumption of both users and UAV decrease,the gaps between two results become smaller.The biggest gaps of users energy consumption and UAV energy consumption are 10 J and 4000 J respectively in the Condition(5),the smallest gaps of users energy consumption and UAV energy consumption are 0.2 J and 1000 J respectively in the Condition(8), the decreasing UAV energy consumption is much more than the increasing user energy consumption.

Comparing the optimized results from Condition(4),9,10,we analyze the impact of data bits number which is shown in Figs. 17 and 18.

As the data bit number increase,both UAV and user energy consumption get greater. UAV energy consumption decrease 5500 J and 4500 J, user energy consumption increase 10 J and 18 J under proposed constraint in condition (9) and (10)respectively.

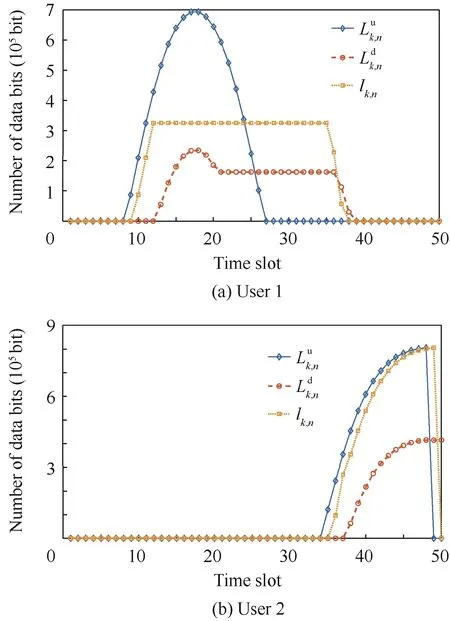
Fig. 6 Optimized data bits with proposed constraint.

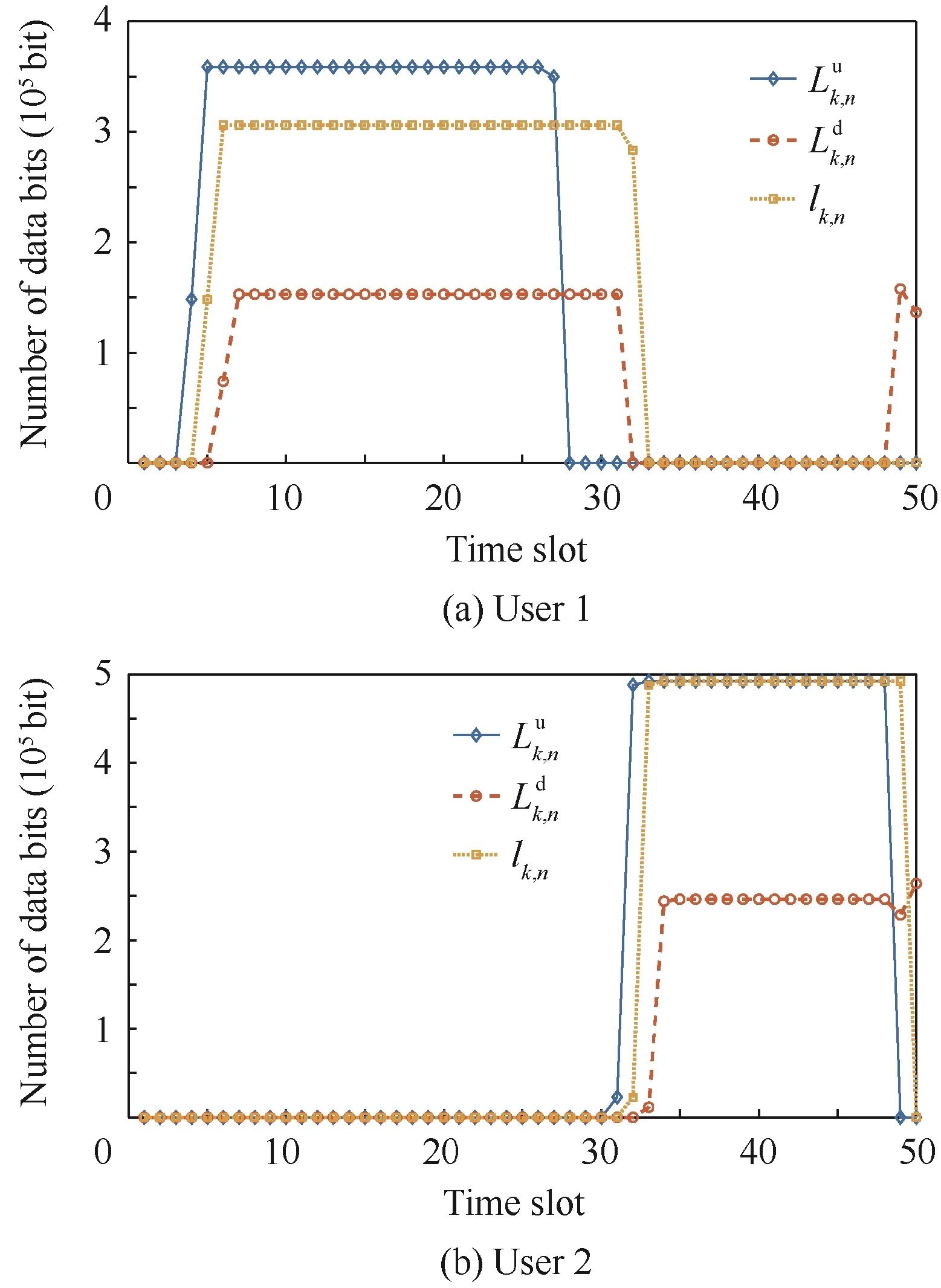
Fig. 7 Optimized data bits without proposed constraint.

Fig. 8 Optimized UAV energy consumption with and without proposed constraint.

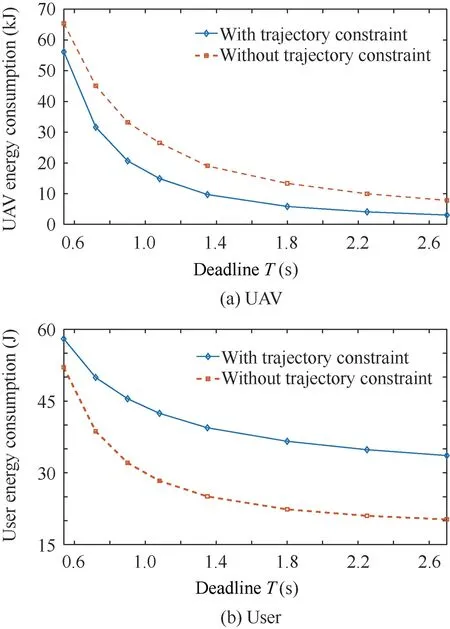
Fig. 10 Optimized results of Condition (2).

Fig. 11 Optimized results of Condition (3).

Fig. 12 Optimized results of Condition (4).

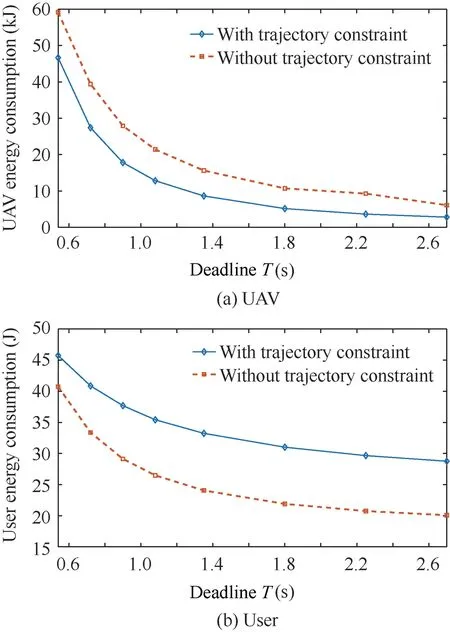
Fig. 13 Optimized results of Condition (5).

Optimized results in all conditions show that UAV energy consumption can be saved 1000 J to 5500 J under proposed trajectory constraint, at the cost of 0.2 J to 18 J more user energy consumption in different energy budget, user position and data bit number,which will increase the UAV service time with almost no impact to users.

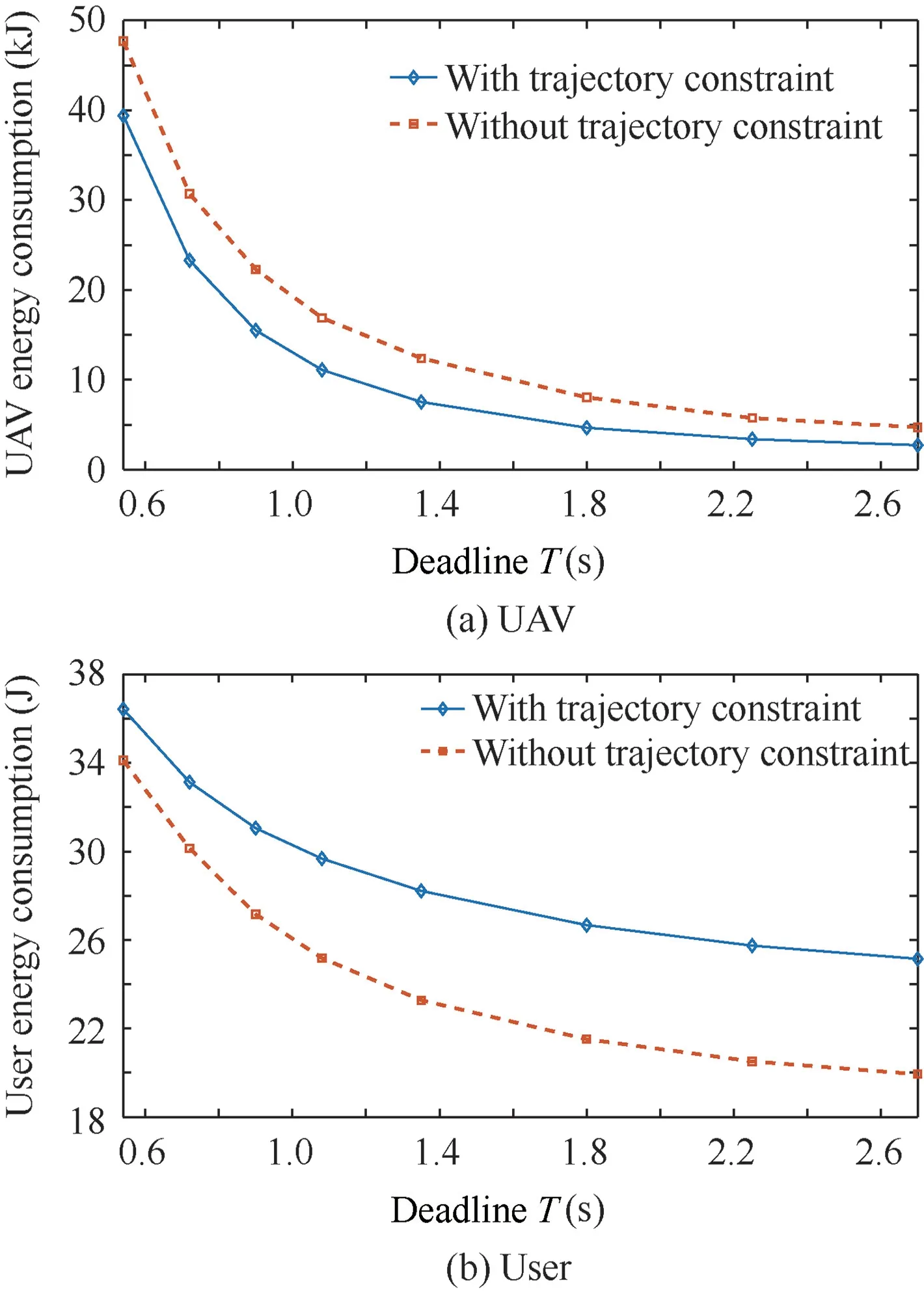
Fig. 14 Optimized result of Condition (6).

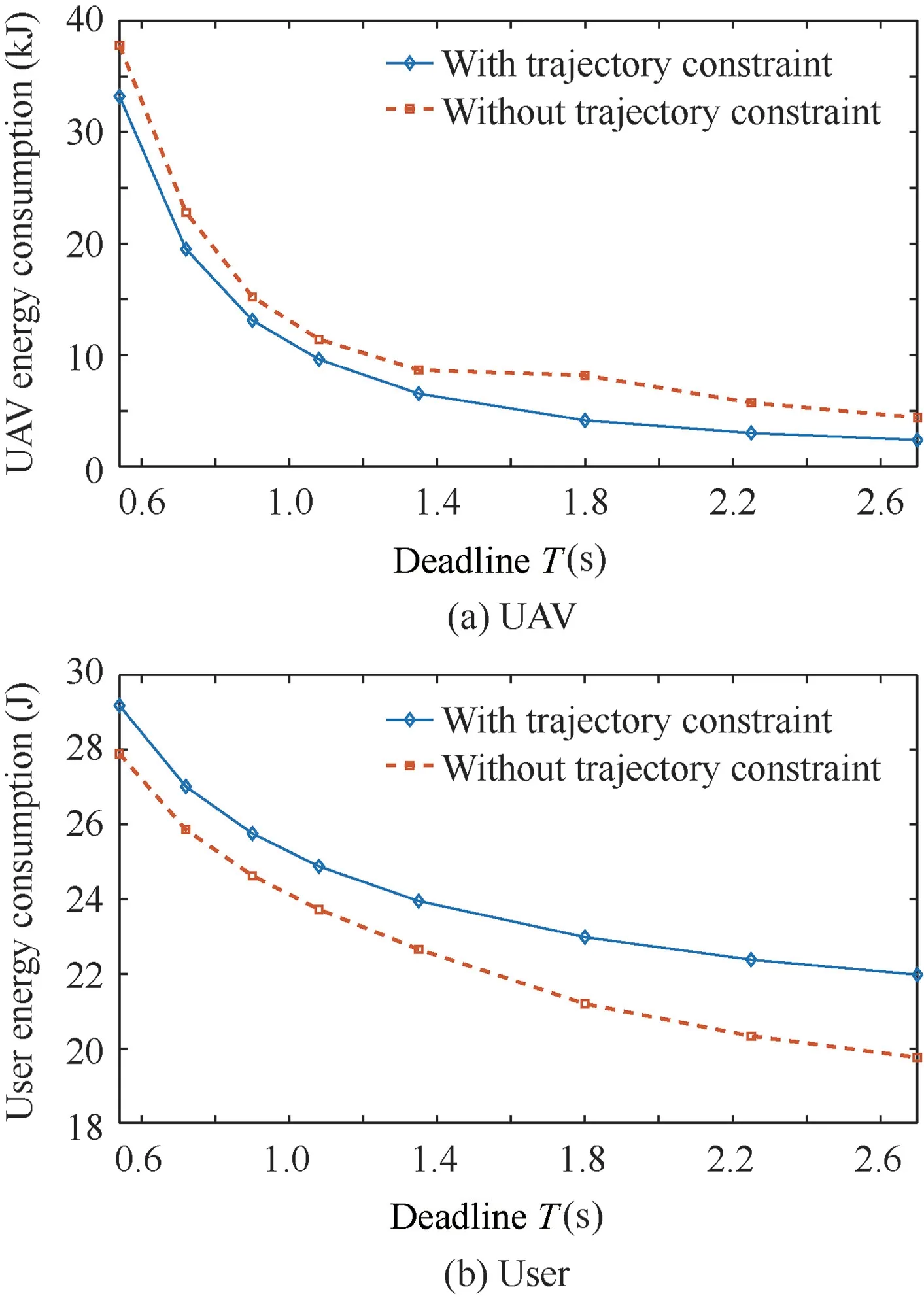
Fig. 15 Optimized result of Condition (7).

What is more, the UAV trajectory with and without proposed constraint in different UAV energy budget and deadline is shown in Figs.19 and 20.In Fig.19,when deadline is 0.54 s,UAV has no enough time to cover all users position and choose the fly over way, as deadline increase, trajectory without proposed constraint become unsmooth and choose to fly right above each user, the trajectory with proposed constraint still keep smooth which is more realistic.

Fig. 16 Optimized result of Condition (8).

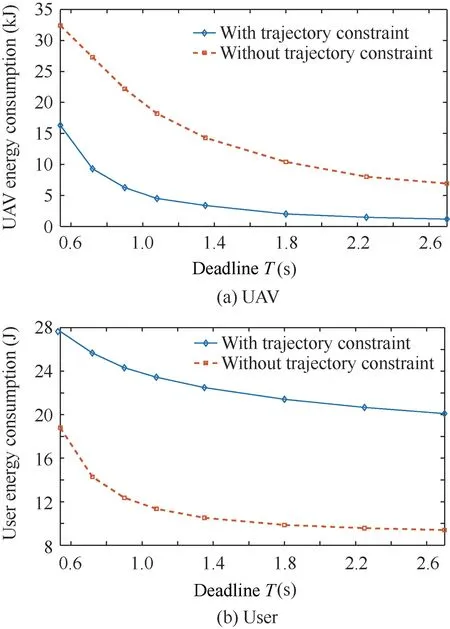
Fig. 17 Optimized result of Condition (9).

Fig. 18 Optimized result of Condition (10).

To validate the performance of ADMM under dynamic UAV energy budget,we compared the optimized results under both constant and dynamic UAV energy budget.The parameters of two conditions are shown in Table 3.The UAV energy budget in condition(11)keep the same at each time slot.Condition (12) simulates the emergency in flight, where the UAV budget decreases suddenly. The deadline T in each condition is 2.25 s. The simulation results are shown in Fig. 21, where the decreasing of budget mainly affects the UAV trajectory.In Condition (12), the UAV changes its direction at time slot 20(the moment of sudden budget change)and plans a smaller loop path to arrive the final position with lower consumption of flying energy. However, the new planning path is further away from users, so that the user energy consumption increases compared with Condition (11).

5. Conclusions

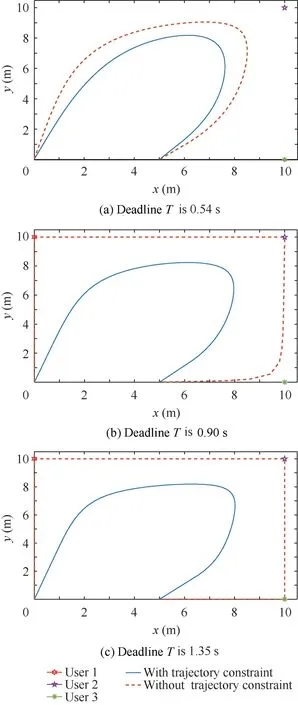
Fig.19 Trajectory in different deadline(energy budget is 60 kJ).

In this paper, we formulate a UAV-enabled mobile edge computing system, which jointly optimizes the bit allocation and UAV trajectory to minimize the energy consumption of users.To generate smoother UAV trajectory and reduce the UAV energy consumption, we propose a trajectory constraint and solve the optimization by the ADMM algorithm. Experimental results demonstrate that the presented ADMM solution performs favorably against the state-of-the-art approaches,while the trajectory constraint leads to a smoother path which is more suitable to the real situation. Besides, compared with the solution without the proposed constraint, the constrained solution can save more UAV energy consumption, i.e.,1000 J to 5500 J.Finally,two comparative conditions are simulated to further indicate the performance of the proposed ADMM under dynamic UAV energy budget.

The work in this paper can draw further research in multi UAV-enabled system to improve the service efficiency. The UAV resource allocation, multi UAV cooperation and thecollision avoidance are challenging and worthy of further study. In addition, the robustness of optimization method should also be considered. Most state-of-the-art methods utilize ideal channel and communication environment, however,data package loss exists in the real situation.The optimization method under non-ideal communication situation will be studied in our future work.

Table 3 Conditions setting under constant and dynamic UAV energy budget.

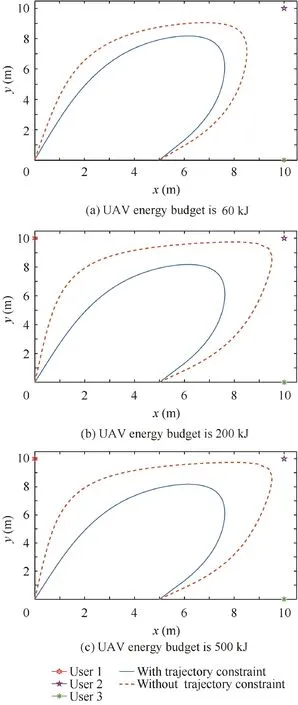
Fig.20 Trajectory in different energy budget(deadline is 0.54 s).

Acknowledgements

This work was supported by the Defense Industrial Technology Development Program of China (No.JCKY2017601C006), the National Key Research and Development Program of China (No. 2016YFB0502602) and the National Natural Science Foundation of China (No.91538204), and in part supported by Shenzhen Science and Technology Program, China (No.KQTD2016112515134654).

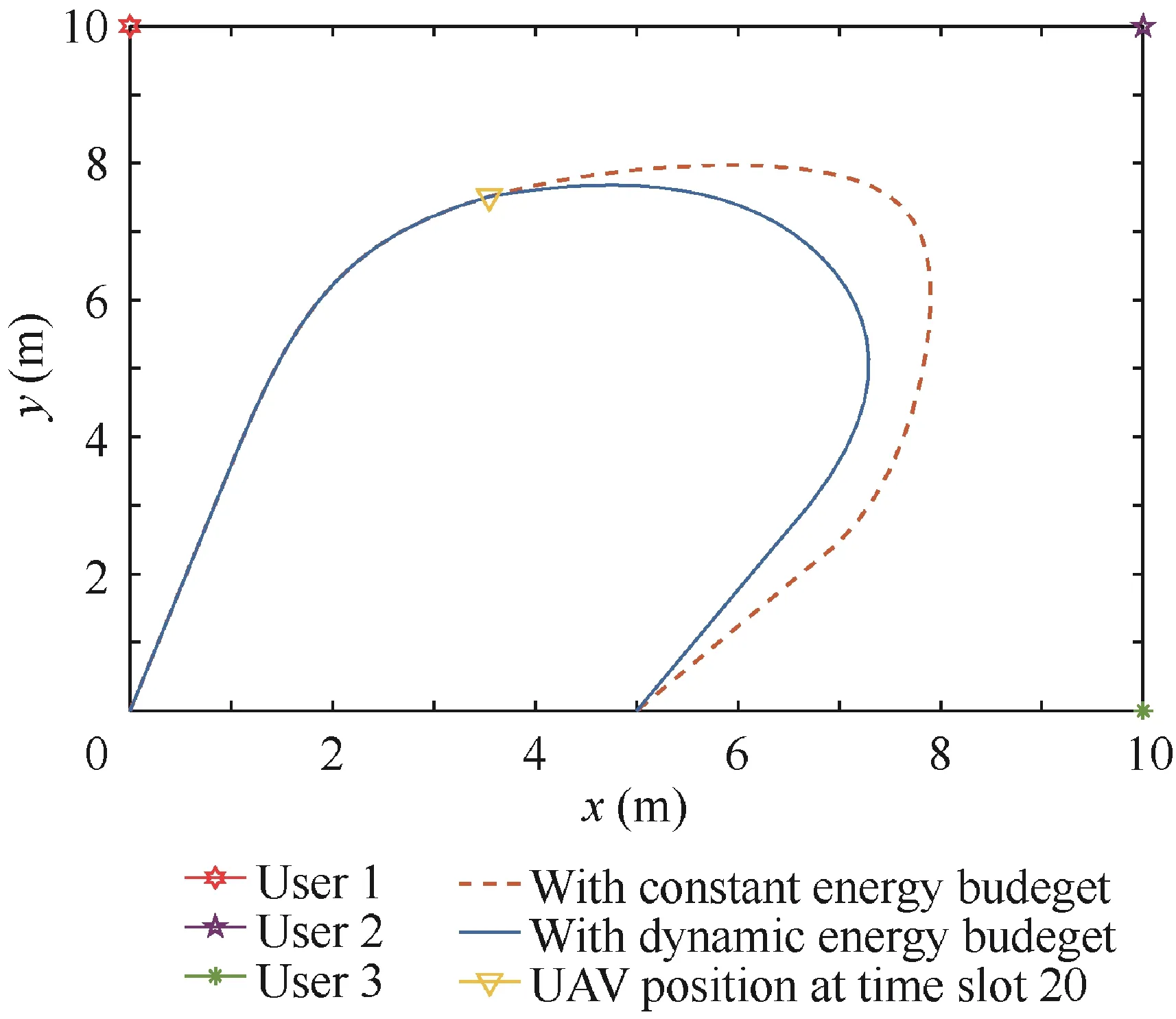
Fig. 21 Trajectory under the dynamic energy budget of UAV.