Orbital maneuver strategy design based on piecewise linear optimization for spacecraft soft landing on irregular asteroids

Zhiwei HAO, Yi ZHAO, Ying CHEN, Qiuhu ZHANG,*

a Department of Astronautical Science and Mechanics, Harbin Institute of Technology, Harbin 150001, China

b Beijing Institute of Control Engineering, Beijing 100190, China

KEYWORDS Irregular gravitational field;Optimal control;Orbital locations;Piecewise linear techniques;Soft landing

Abstract Recently, asteroid exploration becomes an important branch of human’s deep space activities.In this paper,a piecewise linear optimal orbital maneuver strategy is designed for a spacecraft soft landing on irregular-shaped asteroids.First,the space around an irregular asteroid is converted into several grid units,and the gravitational field of the asteroid is linearly fitted in each unit.Then,the soft-landing orbital maneuver strategy design problem is formulated as a piecewise linear optimal problem, and further transferred into a family of two-point boundary value problems,which can be solved using collocation method. Finally, a corresponding algorithm is developed to obtain the piecewise linear optimal maneuver strategy, which is proved to be able to achieve the soft-landing mission well. Simulation results show that the error of the model linearization is small enough, while the calculation efficiency is remarkably improved, and the robustness of maneuver strategy is also improved.

1. Introduction

Space powers began to focus their deep space exploration on a large number of asteroids in the solar system in recent years.In 2001, NASA’s NEAR-Shoemaker spacecraft landed on the asteroid Eros 433.1Then in 2005, Japanese spacecraft Hayabusa touched down on asteroid Itokawa.2The second Chinese lunar probe Chang’e-2 conducted a flyby of the asteroid Toutatis on 13th December, 2012,3and Chang’e-5T1’s extended mission may also include another flyby of an asteroid.4The exploration of asteroids has important science significance since asteroids may contain the key information on the origin of life in the solar system and the earth. Meanwhile, asteroids may contain large amounts of the Earth’s scarce resources or essential materials for the interstellar navigation. These resources provide a material basis for human industrial development or future interstellar navigation if human beings can collect them by soft landing on the asteroids.5Therefore, the realization of soft landing on asteroids is an important part of deep space exploration missions.

Different from large celestial bodies, asteroids tend to be less massive and more irregular-shaped.Therefore,the gravitational fields of asteroids are also weak and irregular. Such a gravitational field makes the orbital evolution of the spacecraft around asteroids more complex and easier to be affected by various perturbing forces.Scheeres studied the orbital mechanics of spacecraft around the asteroids and analyzed the orbital evolution of spacecraft under the effects of asteroid attractive force and solar perturbation, respectively. The results showed that the spacecraft may escape from the asteroid or impact on the asteroid.6He also carried out researches on the design of the low-altitude flying around orbit and landing trajectories and proposed several main considerations for the trajectory design.7Jiang and Baoyin. investigated the dynamic equations,8equilibrium points,9orbits and manifolds near the equilibrium points,10and(stable)periodic motion around irregular asteroids.11,12Liang et al. constructed homoclinic/heteroclinic connections of equilibrium points of different types and a lowcost orbits transfer strategy,13and stabilized motions near a special type of equilibrium point by Hamiltonian structurepreserving control for contact binary asteroids.14Melman et al. studied the error transfer from the uncertainty of the gravitational field of an asteroid to the state of a spacecraft based on Monte Carlo algorithm.This method can be adopted to assess the risk of the designed trajectories, which has guiding significance for the risk assessment and orbit selection.15Winkier introduced the filtering state and treated the weak gravitational field of asteroids as a periodic disturbance, and the fuel-efficient optimal orbital control strategy was obtained.16Guelman and Harel regarded the asteroid as a sphere, and obtained a fuel optimal guidance strategy, which assures a vertical soft landing on the asteroid.17Yang and Baoyin transformed the energy optimal control problem of soft landing into a Two-Point Boundary Value Problem(TPBVP)and solved the TPBVP by using the fast homotopical method to achieve the soft landing.18Ren and Shan introduced the model error caused by the uneven mass distribution of asteroids and treated the optimal control problem as a parameter optimization problem. The optimal landing orbital control was realized through a series of optimization and stability evaluation.19Dunham et al. reduced the original nonlinear dynamic equations into linear forms by using a uniform density ellipsoid model and the linearization error is regarded as the disturbance term. Then the input state observer was adopted to eliminate the disturbance so that the soft landing on asteroids was also achieved.20Furfato et al. proposed a multiple sliding surface guidance algorithm based on high-order sliding-mode control theory to achieve asteroid precision landing, which is demonstrated accurate and flexible.21

Due to low mass and the uneven mass distribution of asteroids, the gravitational fields of irregular asteroids are strong nonlinear. Soft landing on an asteroid is naturally a strong nonlinear problem. The existing methods mentioned above can solve the problem of orbital maneuvering for spacecraft soft landing on irregular asteroids to some extent. Although many improved methods have been proposed to solve such kind of nonlinear problems,22,23the solving process is often complicated and time consuming due to strong nonlinearity and high dimension of the model, which makes it difficult to realize the real-time control of the spacecraft. On the other hand, the open-loop orbital maneuver strategy is less robust.In fact, the observed state often has errors caused by instruments and measurement techniques.

This paper proposes a method to transfer the original nonlinear problem into a piecewise linear one,and develops a corresponding algorithm to solve the problem for optimal orbital maneuver strategy. The space around the irregular asteroid is divided into multiple units and the linear function is adopted to fit the gravitational field in each unit.Therefore,the nonlinear gravitational field is transformed into a piecewise linear gravitational field so that the nonlinear problem of soft landing on asteroids (a nonlinear TPBVP) is transformed into a family of linear TPBVPs. This procedure simplifies the softlanding problem.At the same time,the robustness of the orbital maneuver strategy is improved by computing it multiple times in different units of gravitational field. This is because the observed state is used multiple times for piecewise optimal orbital control, and it is a bit similar with the state feedback control. The simulation results show that the piecewise linear optimal orbital maneuver strategy proposed in this paper deduces the computational time greatly and has no significant increase in energy consumption compared with the energy optimal orbital maneuver strategy. Due to the promotion of calculation efficiency and robustness, it is possible to apply the proposed method for real-time control over the spacecraft during the soft-landing mission, which increases the success rate of the mission.

The paper is organized as follows. Section 2 introduces the gravitational field models of asteroids and establishes the dynamics equation of the spacecraft in the asteroid bodyfixed coordinate. Section 3 proposes a piecewise linear orbit maneuver strategy by dividing the space into multiple units.In Section 4, the asteroid Eros 433 is taken as an example to verify the computational efficiency and robustness of the proposed method. Section 5 summarizes the paper.

2. Problem formulation

In this section, two conventional types of asteroid gravitational field models are introduced, and the dynamic equation of a spacecraft around an irregular asteroid with perturbations is established.

2.1. Gravitational field models of asteroids

The volume and mass of asteroids are often small, and their shapes are highly irregular, so the calculation of gravitational field of an irregular asteroid is complicated. There are two commonly used methods for calculating the gravitational field of asteroids: the spherical harmonic model24and the polyhedral model,25and they are introduced briefly as follows.

2.1.1. Spherical harmonic model

The spherical harmonic model is a method widely used for modeling gravitational fields of large celestial bodies. If the spherical harmonic model is adopted to compute the gravitational field,the space near the asteroid needs to be divided into an exterior Brillouin sphere and multiple interior Brillouin spheres as shown in Fig.1.The reason is that the spherical harmonic function is not globally convergent for asteroids with irregular shape.Outside the exterior Brillouin sphere,the gravitational potential energy function at the point which is r away from the center of exterior Brillouin sphere with the latitude φ and longitude λ can be written as

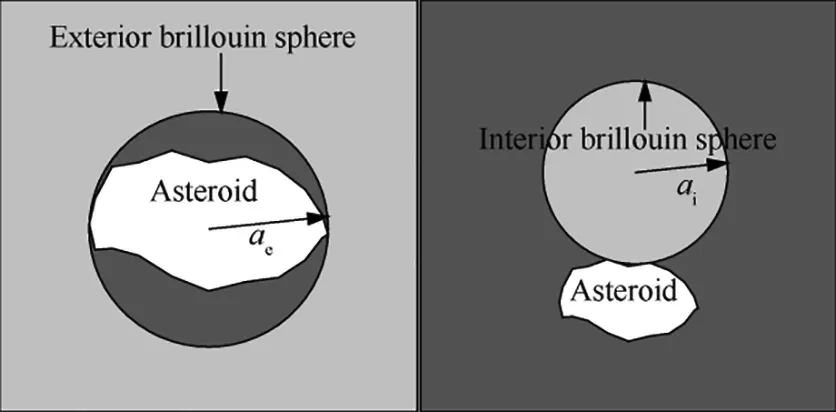
Fig. 1 Sketch map of Brillouin sphere.

2.1.2. Polyhedral model

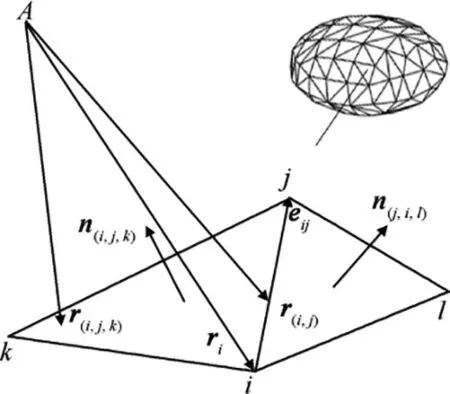
Fig. 2 Illustration of elements of polyhedral model.

2.2. Dynamic equations of spacecraft

The dynamic equation of an uncontrolled spacecraft near an asteroid in the inertial coordinate system is

where r denotes the position vector of the spacecraft relative to the asteroid centroid, U is the gravitational potential energy function of the spacecraft, R denotes the potential function of other perturbations acting on the spacecraft,R mainly contains the potential function of the solar radiation pressure Rsrpand the solar gravitational perturbation Rs, and they can be expressed as6

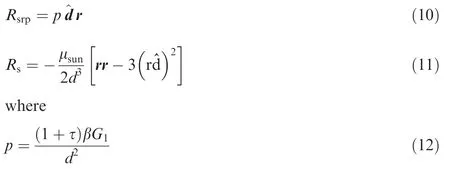
where τ is the reflectance of the spacecraft,G1is the a constant related with the radiation flux of the Sun, β is the area-mass ratio of the spacecraft, μsunis the gravitational constant of the Sun, d is the distance from the Sun to the asteroid, and ^d is the unit vector from the solar centroid to the asteroid centroid.

After a long period of the orbital evolution of an asteroid,the asteroid will rotate uniformly around the rotating axis about which the moment of inertia is maximal.6Therefore, a coordinate system fixed to the asteroid can be established as in Fig. 3, whose origin O is the asteroid centroid, the rotation axis is set to be z axis,the axis about which the moment of inertia is minimal is selected to be x axis,and y axis is chosen so that O-xyz consists of a right-hand system. In this asteroid-fixed coordinate system (a moving coordinate system), dynamic equation of an uncontrolled spacecraft can be written as

and then the dynamic equation of the spacecraft in the component form is obtained:

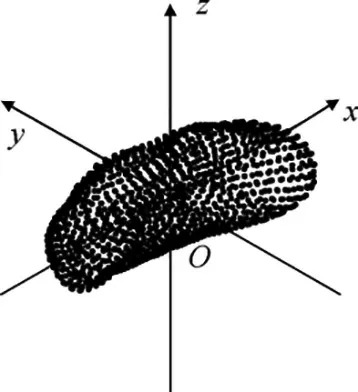
Fig. 3 Illustration of coordinate system fixed to the asteroid.

3. Piecewise linear optimal orbital maneuver strategy design

This section introduces a conventional method transforming the optimal control problem into a TBPVP first. Second, the gravitational field of the space around the irregular asteroid is approximated by piecewise linear fitting.Therefore,the nonlinear problem of soft landing on asteroids is transformed into a family of linear TPBVPs.The proposed method simplifies the soft-landing problem and improves the robustness of the orbital maneuver strategy.

3.1. Optimal control problem

For dynamic Eqs. (17)-(18), the state at the initial time t0and the terminal time tfof the soft landing process are given as

where H （·） represents the partial differential ∂H/∂（·）. Substitute u（t ） in Eq. (24) into Eq. (22), and the Hamiltonian function can be written as

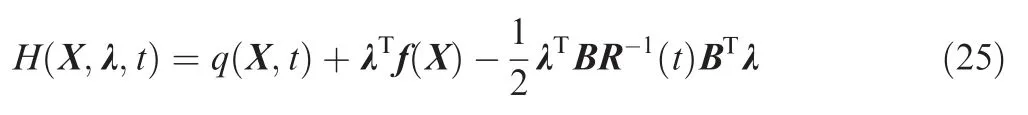
and the differential equations that X and λ satisfy are

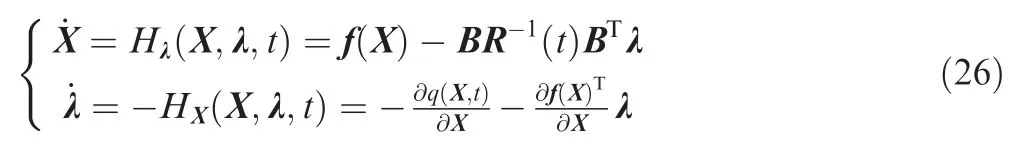
Thus, the optimal control problem described in Eqs. (17)-(20) is transformed into the TPBVP in Eq. (26) with the boundary value conditions in Eq. (19). The optimal control input in Eq. (24) can be determined by solving TPBVP for the costate λ.

In addition to the Pontryagin minimum principle, which is a kind of indirect method to solve the optimal control problem, the direct methods, such as the convex optimizationbased method, can also be applied to solve the problem described by Eqs. (17)-(20)for some certain cases.35,36In Section 4.2.1, the convex optimization method is also adopted to compare with the method based on the Pontryagin minimum principle.

3.2. Piecewise linear optimal orbital maneuver strategy

Substituting the asteroid gravitational field described by the spherical harmonic model or the polyhedral model into the dynamic equation of the spacecraft in Eq. (17), the optimal orbital maneuver strategy of the spacecraft can be obtained by solving TPBVP in Eq. (26) with the given boundary condition in Eq. (19) directly using numerical method such as the shooting method37and the collocation method.37,38However,since the gravitational field of asteroids is fairly irregular and strong nonlinear, the process of solving nonlinear TPBVP is complicated and takes long time, which is unfavorable for real-time calculation of orbital maneuver strategy. Besides,the orbital maneuver strategy obtained by the direct numerical method is an open-loop control strategy, which is less robust and requires high accuracy of state observation. In fact, the spacecraft is easily affected by various disturbance factors in the space environment, which leads to the inaccuracy of the state of spacecraft. Once there is error of the state, the spacecraft could not land on the designed point.

To reduce problem solving complexity and computing burden and improve the robustness of the orbital maneuver strategy, this paper divides the space around the asteroid into several units, as shown in Fig. 4, and fits the gravity of the asteroid by linear function in each unit,i.e.in unit Ei,the gravity is fitted as

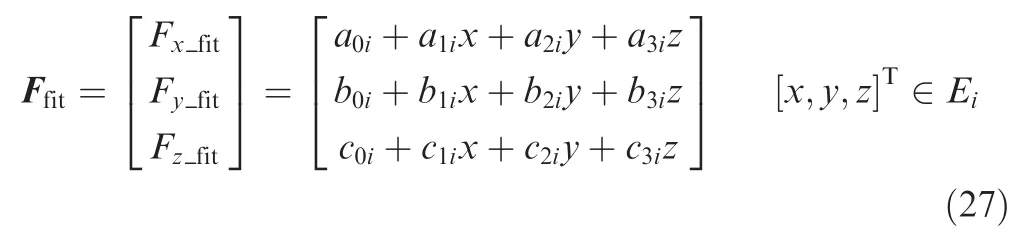
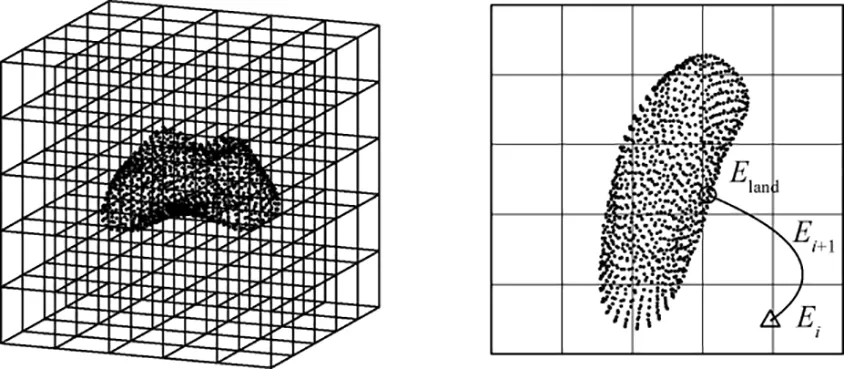
Fig. 4 Sketch map of unit division.

The coefficients a0i-a3i,b0i-b3i,and c0i-c3iare obtained by the least square fitting. The dynamic equation of the spacecraft in Eq. (17) can be written as

The spacecraft is very close to the asteroid during the softlanding period. So other perturbations are negligible comparing with the gravity of the asteroid.If the fitting error is small enough,it can also be ignored when solving the orbital maneuver strategy.Then,nonlinear terms are removed in the dynamic equation of the spacecraft in Eq.(28),and the nonlinear system is converted to a linear one in the unit Ei, so the problem is simplified.

By defining ti0as the time when spacecraft entries the unit Ei, the state at this time is

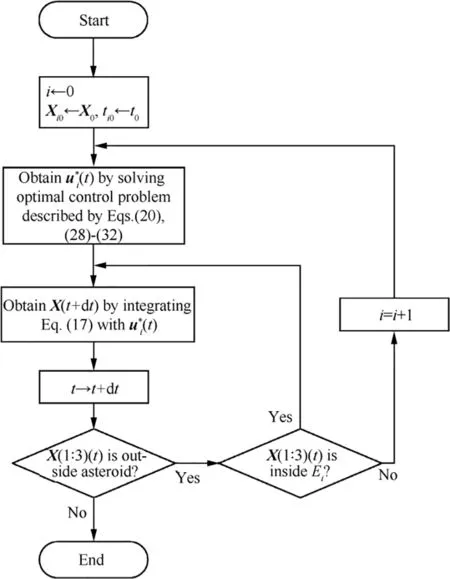
Fig. 5 Flowchart of algorithm for solving piecewise linear optimal maneuver strategy problem.

According to the method solving the orbital maneuver strategy proposed in this section, the continuous nonlinear control problem is transformed into a piecewise linear orbital maneuver problem, which simplifies the original problem and greatly reduces the computational time. It is suitable for real-time control of the spacecraft.At the same time,the error caused by the inaccurate state observation can be reflected in the state vector when the spacecraft enters the next unit.After recalculating the subsequent orbital maneuver strategy, it can be eliminated partly, thus improving the robustness of the maneuver strategy. The orbital maneuver strategy proposed in this subsection is not a global optimal strategy,but the simulation results in the next section show that the energy consumption of the proposed strategy is basically the same with the global optimal orbital maneuver strategy obtained by solving the original nonlinear problem directly.

4. Simulation results for the asteroid Eros 433

Eros 433 is a near-Earth asteroid in the solar system with a large orbital eccentricity. The perihelion is inside the Martian orbit, and the aphelion is far beyond the Martian orbit. The United States launched the NEAR-Shoemaker satellite to detect the Eros 433 in 1996. NEAR-Shoemaker satellite went into orbit in 2000,and finally landed on Eros 433 after a series of detections. According to the detection results of NEARShoemaker, the model of Eros 433 can be constructed with great precision,as shown in Fig.6.Therefore,this paper takes Eros 433 as an example to verify the effectiveness of the proposed orbital maneuver strategy. The shape and other basic information of the Eros 433 can be downloaded in NASA website.39

The semi-major axis of the revolve orbit of Eros 433 is 1.458 A.U. (1 A.U.=1.496×108km). According to Eqs. (10)-(12), the magnitude of solar radiation pressure and solar gravitational perturbation near Eros 433 can be estimated as follows. Assume that τ equals 0.3 and β equals 0.1 m2/kg in Eq. (12). The solar radiation pressure executed on the spacecraft is about 2.691×10-7m/s2. If the spacecraft is 20 km away from the centroid of Eros 433, the maximum solar gravitational perturbation is about 1.024×10-9m/s2.Meanwhile, the acceleration due to the attraction of Eros 433 at the point (20, 0, 0) km is 1.686×10-3m/s2, which is much larger than the solar radiation pressure and the solar gravitational perturbation. Thus, the solar perturbations are neglected in the following simulations.

4.1. Description of numerical example

The fixed coordinate system is established with the asteroid Eros 433 rotation axis as the z axis, and minimum inertia as x axis, as shown in Fig. 6. Two scenarios are designed in this section. The first one assumed that the spacecraft is hovering above the asteroid with a distance of 20 km from the centroid of Eros 433 in x-y plane before the start of soft-landing procedure, as shown in Fig. 7. Take the soft-landing point as(-4.050, -3.576, 0) km, which is located in a relatively flat area in the middle of Eros 433 and is suitable for landing and exploration work nearby, and the starting point of the landing trajectory as (-5.176, -19.32, 0) km, which is above the designed landing point. The initial velocity is (0, 0, 0) m/s.

In the second scenario,the spacecraft is assumed to revolve around the asteroid on the 20 km orbit in y-z plane before the start of soft-landing procedure.The starting point is chosen as(0, -14.14, 14.14) km, and the initial velocity is (0, -3.339,-3.339) m/s. The soft-landing point is also selected as(-4.050, -3.576, 0) km. The sketch map of this scenario is shown in Fig. 8.

In the first scenario, the cost function is chosen as

In the following simulations, take t0=0 s and tf=3000 s for both cases, which means that the spacecraft completes the soft landing process within 3000 s.

4.2. Simulation results of piecewise linear orbital maneuver strategy

4.2.1. Simulation results of the first scenario

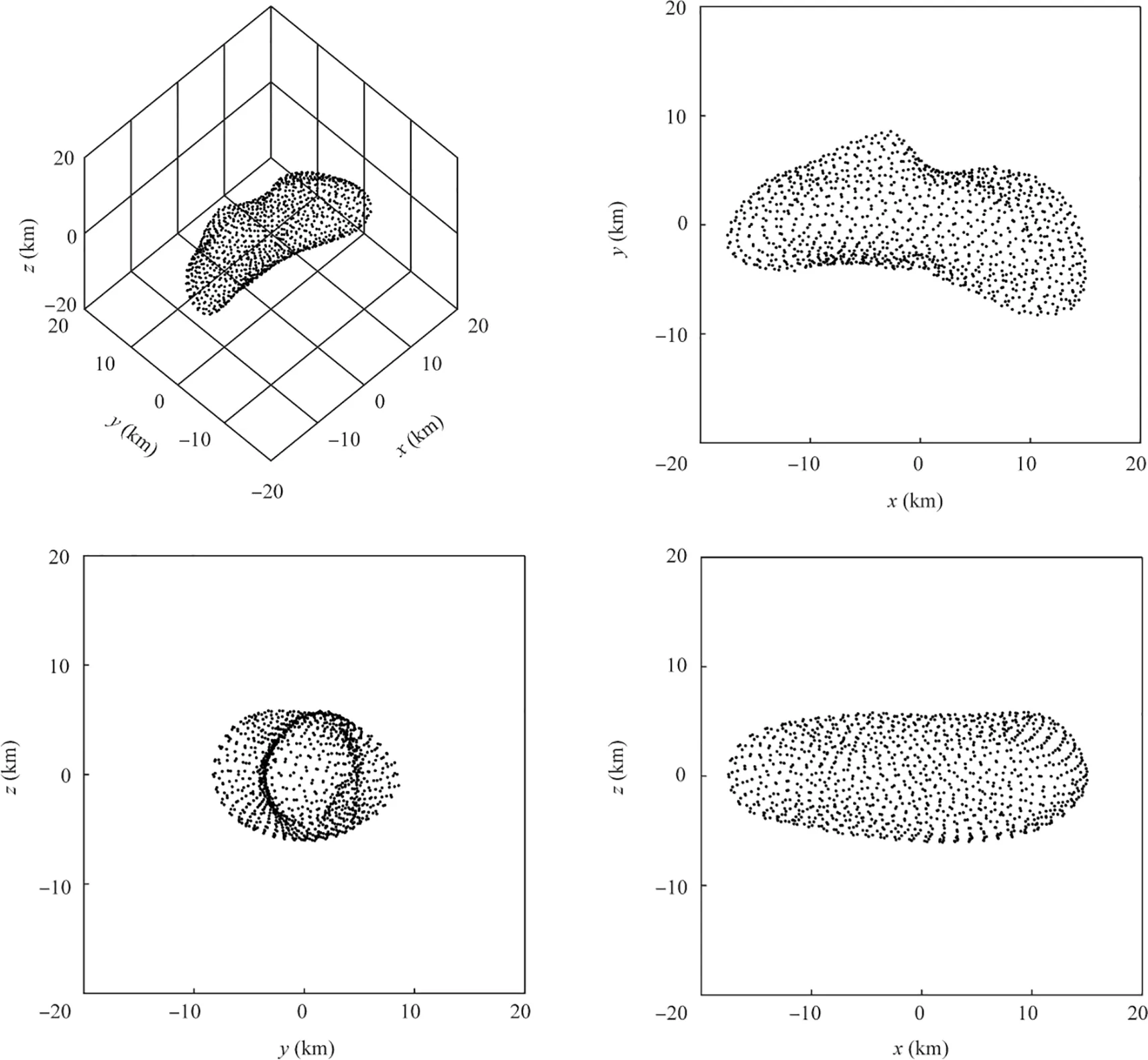
Fig. 6 Illustrative diagram and three-view drawing of Eros 433.

Considering both of the computational efficiency and fitting accuracy, the space around the Eros 433 is divided into a plurality of cube elements with a side length of 500 m.Because the space range spans the exterior and interior Brillouin spheres,it is more complicated to calculate the gravitational field using the spherical harmonic model. Therefore, the gravitational field of Eros 433 is computed by the polyhedral model.In each unit,the gravitational acceleration of 27(3×3×3)points are computed,and then the coefficients in Eq.(27)are linearly fitted using the previous data by the least square fitting. In this way, the maximum fitting error is 1.0%. The ‘‘bvp4c” command in MATLAB (using the collocation method) is used to solve the TPBVP, and the orbital maneuver strategy is obtained. Meanwhile, the polyhedral model is brought into Eq.(17)to solve the nonlinear orbital maneuver strategy problem directly,and the results are compared with the ones by the method proposed. For the first scenario, the convex optimization-based method is also adopted to solve the piecewise linear problem. CVX, a package for specifying and solving convex programs,40,41is used as the solver for the convex optimization-based method. The landing trajectories in x-y plane are shown in Fig. 9, the displacement, velocity and control trajectories of the spacecraft with respect to time t are shown in Fig. 10, and the computational results are shown in Table 1.Since the piecewise linear optimal maneuver strategies solved by collocation method and convex optimization method are almost the same, and the corresponding trajectories are hard to be distinguished in Fig.10,only the trajectories obtained by collocation method are plotted in Fig. 10. It can be seen from Fig. 9 and Fig. 10 that the actual trajectory of the spacecraft using the piecewise linear optimal maneuver strategy is almost the same with the one under the optimal maneuver strategy obtained by solving the nonlinear control problem directly. Finally, both of the two strategies achieve the soft-landing mission. It is noted that the spacecraft lands on the asteroid surface in 2982 s (18 s ahead of the designed landing time 3000 s) by adopting the piecewise linear orbital maneuver strategy solved by collocation method. This is due to the piecewise linear gravitational field model which has small error compared with the actual one. The actual landing point is 2.333 m away from the designed landing point and the landing speed is 0.2206 m/s for the piecewise strategy solved by collocation method. And for the strategy solved by convex method, the distance from the designed landing point is 5.470 m, and the landing speed is 0.01045 m/s. The softlanding task can be well accomplished by using the piecewise linear orbital maneuver strategy considering the size of the asteroid.

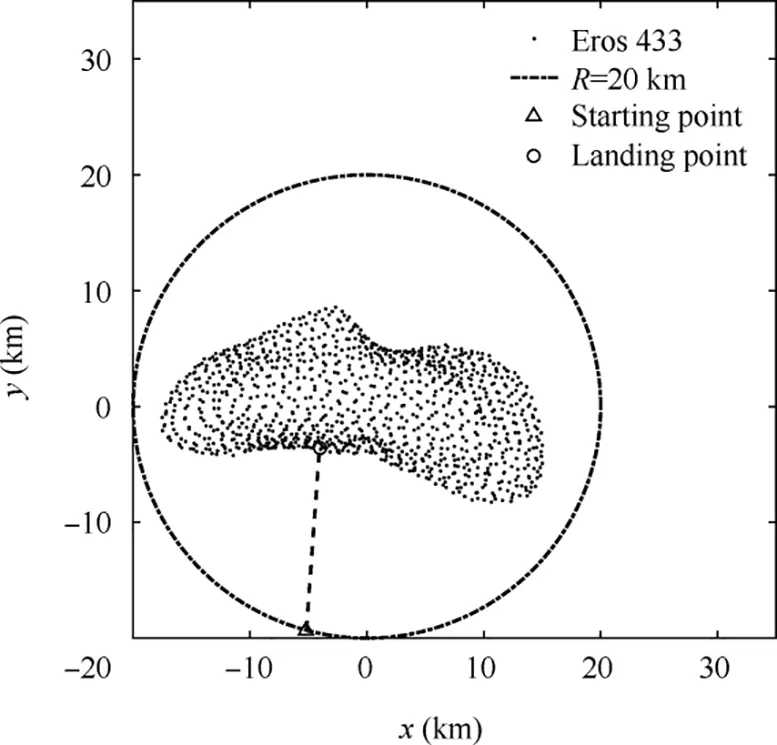
Fig. 7 Sketch map of soft landing for the first scenario.

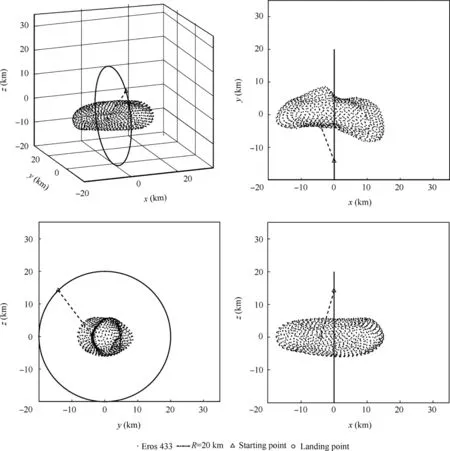
Fig. 8 Sketch map of soft landing for the second scenario.

The spacecraft passes through 40 units of the gravitational field throughout the soft-landing process, so the control strategy is calculated 40 times to obtain the piecewise linear orbital maneuver strategy. The total calculation time for collocation method is 28.98 s, while for convex method, the calculation time is 93.06 s in total.Under the same calculation conditions,the time required for solving the nonlinear orbital maneuver strategy directly is 29815 s. It can be seen that the proposed method can greatly improve computational efficiency of the orbit maneuver strategy and facilitate the real-time control of the spacecraft. The calculation efficiency of collocation method is a bit higher than that of the convex method, and thus the collocation method is more capable for real-time control. In the rest parts of this paper, the‘‘piecewise linear strategy” denotes the piecewise linear optimal maneuver strategy solved by collocation method.

An index JErelated with the energy consumption during the landing process is defined as

The value of JEis 0.1022 by solving the nonlinear orbital maneuver problem directly, while the one is 0.09991 by utilizing the proposed method solved by collocation method, and 0.1022 by solving the piecewise linear problem by convex method,which is no more than the energy consumption under the global optimal orbital maneuver strategy.

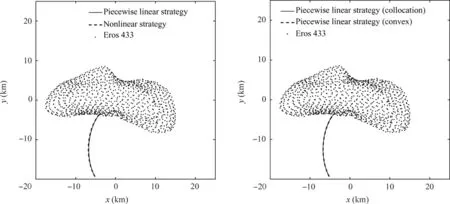
Fig. 9 Soft-landing trajectory of spacecraft for the first scenario.

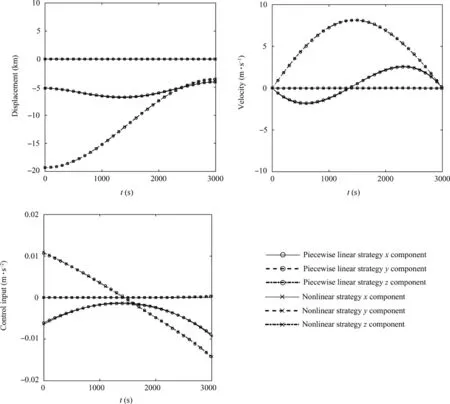
Fig. 10 Time-varying diagram of states and control inputs of spacecraft during soft-landing process for the first scenario.

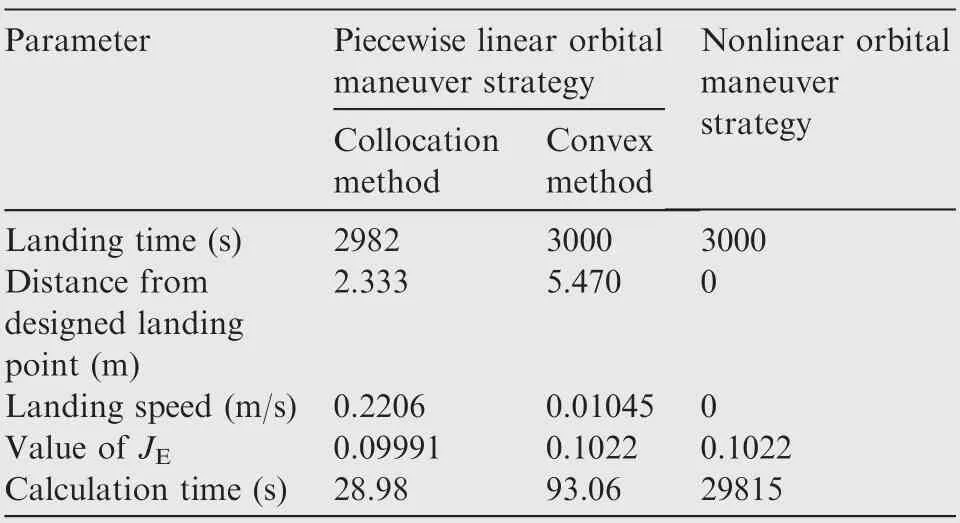
Table 1 Comparison of orbital maneuver strategies during soft landing process for the first scenario.

4.2.2. Simulation results of the second scenario

Simulation is executed for the second scenario with the procedure mentioned in Section 4.2.1. The landing trajectories are shown in Fig.11,the displacement,velocity and control trajectories of the spacecraft with respect to time t are shown in Fig. 12, and the computational results are shown in Table 2.By adopting the piecewise linear orbital maneuver strategy,the spacecraft lands on the asteroid in 2995 s, the landing speed is 6.404 cm/s, and the actual landing site is 0.6723 m away from the designed one. The spacecraft passed 62 units during the whole process, and the total calculation time is 31.03 s, while it costs 38235 s to solve the nonlinear problem.JEis 0.1132 and 0.1138 for piecewise linear orbital maneuver strategy and nonlinear orbital maneuver strategy respectively.Similar conclusion can be drawn by the simulation results that the piecewise linear orbital maneuver strategy can achieve the soft-landing mission well, and can reduce the calculation time in a large scale, which is feasible for real-time control.

4.3. Robustness of piecewise linear orbital maneuver strategy

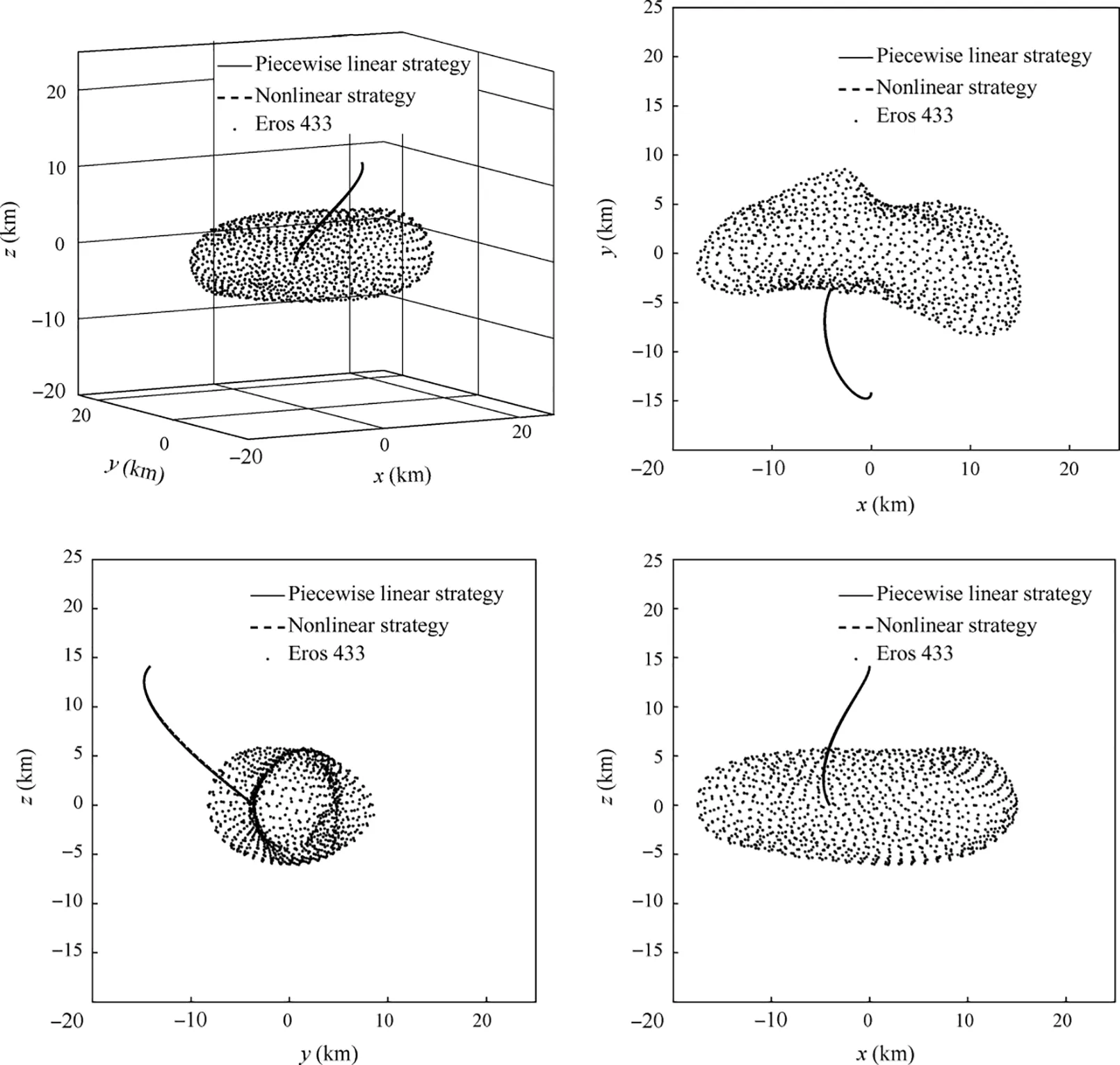
Fig. 11 Soft-landing trajectory of spacecraft for the second scenario.

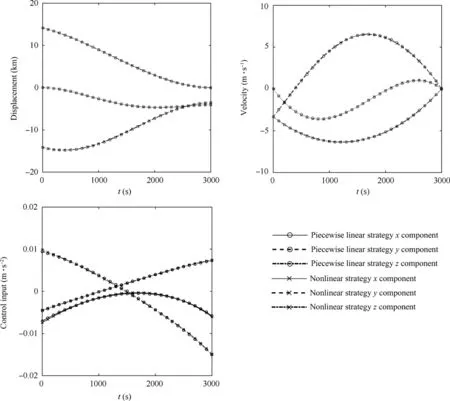
Fig. 12 Time-varying diagram of states and control inputs of spacecraft during soft-landing process for the second scenario.

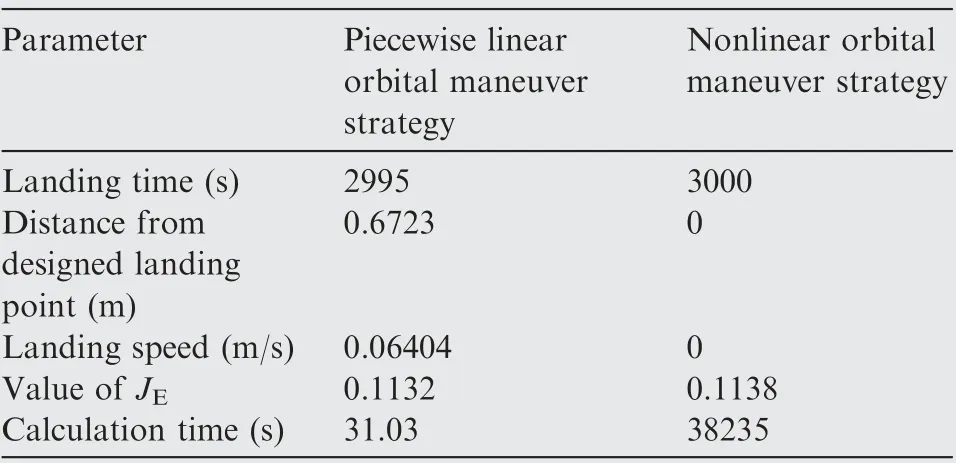
Table 2 Comparison of orbital maneuver strategies during soft-landing process for the second scenario.

In the actual deep space exploration missions,the motion state of the spacecraft can be easily interfered by various perturbations.In addition,the accuracy of the spacecraft’s observation of its own motion state may also be affected by factors such as equipment and communication, and these factors will affect effectiveness of the strategy. This subsection assumes that a 3% deviation exists in the observation of the motion state of the spacecraft, i.e.

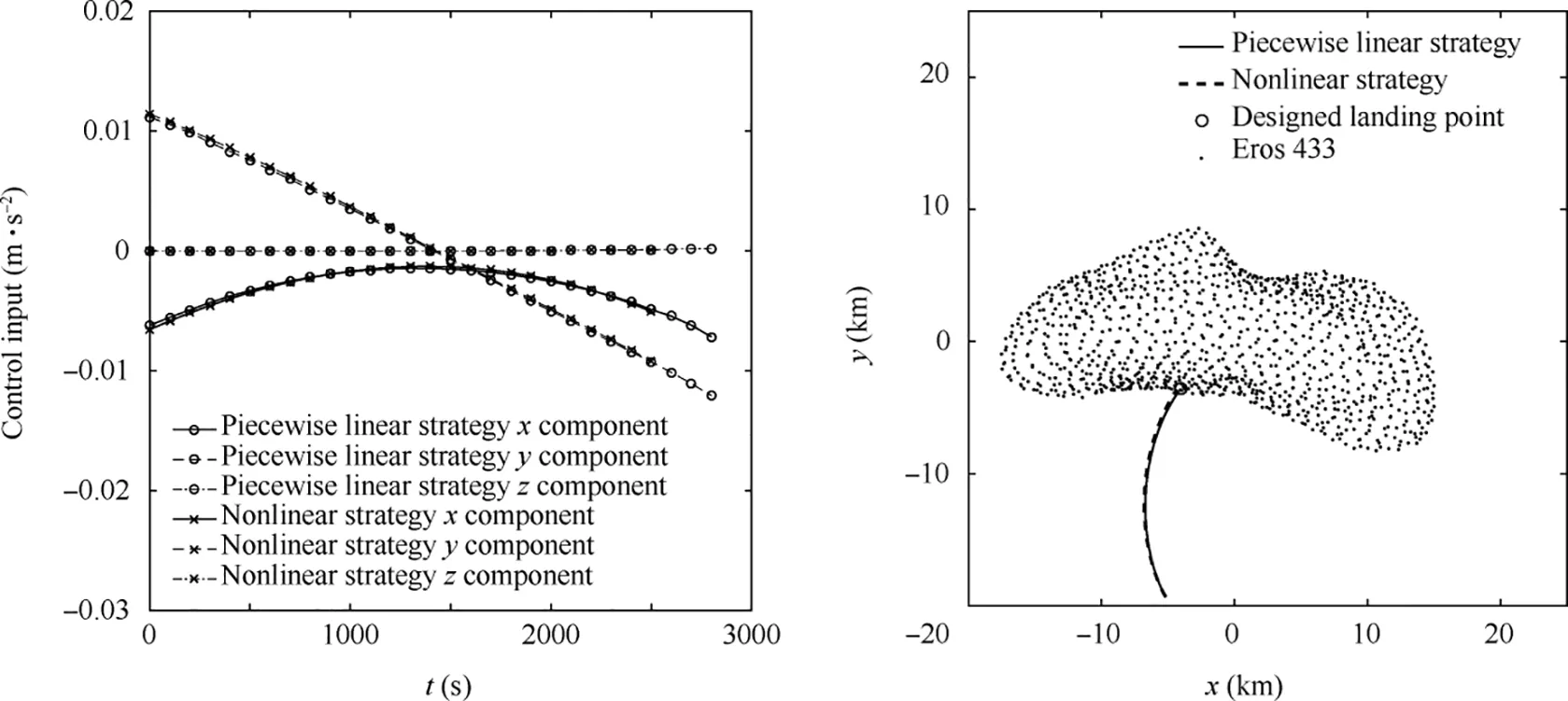
Fig. 13 Trajectories of control input and state in x-y plane under inaccurate state observation.

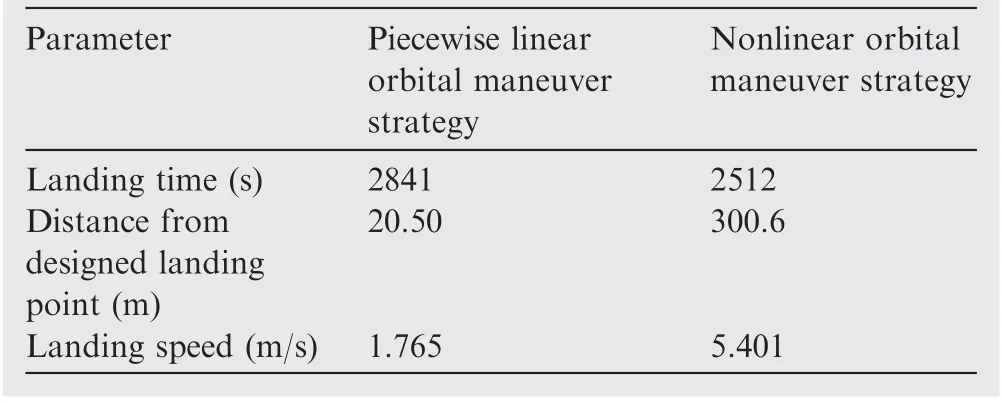
Table 3 Simulation results of soft landing under inaccurate state.

5. Conclusions and future work

This paper proposes a method to transform a nonlinear orbital maneuver strategy problem into a piecewise linear orbital maneuver strategy problem for the spacecraft soft landing on irregular asteroids.The proposed method reduces the difficulty of solving the two-point boundary value problem and greatly improves the computational efficiency compared with the method solving the problem with asteroid’s nonlinear gravitational field.Meanwhile,the robustness of the orbital maneuver strategy is improved by using the proposed method. The simulation results show that the proposed piecewise linear optimal orbital maneuver strategy achieves the soft space landing mission well, and the two characters mentioned above are proved as well. The simulation results also show that, compared with the global optimal orbital maneuver strategy, the energy consumed by the proposed piecewise linear optimal orbital maneuver strategy does not increase significantly. In future researches, more efforts will be paid to achieve higher precision. Solar perturbations should be considered, and disturbance-accommodating control may be introduced to eliminate the perturbations so that the method can be more practical.In addition to the energy-optimal maneuver strategy problem with free thrust magnitude, the constrain on thrust magnitude and fuel-optimal maneuver strategy problem will be investigated in future work as well.

Acknowledgements

This study was supported by the Fundamental Research Funds for the Central Universities, China (No. HIT. NSRIF.201620).This research has made use of the Small Bodies Data Ferret (http://sbn.psi.edu/ferret/), supported by the NASA Planetary System.