Three-axis coupled flight control law design for flying wing aircraft using eigenstructure assignment method

Lixin WANG, Ning ZHANG, Ting YUE, Hiling LIU,*, Jinghui ZHU,Xiopeng JIA

a School of Aeronautics Science and Engineering, Beihang University, Beijing 100083, China

b Chinese Flight Test Establishment, Xi’an 710089, China

KEYWORDS Drag rudder;Eigenstructure assignment;Flight control law;Flying wing;Three-axis coupled

Abstract Due to elimination of horizontal and vertical tails,flying wing aircraft has poor longitudinal and directional dynamic characteristics.In addition,flying wing aircraft uses drag rudders for yaw control, which tends to generate strong three-axis control coupling. To overcome these problems, a flight control law design method that couples the longitudinal axis with the lateraldirectional axes is proposed. First, the three-axis coupled control augmentation structure is specified. In the structure, a ‘‘soft/hard” cross-connection method is developed for three-axis dynamic decoupling and longitudinal control response decoupling from the drag rudders;maneuvering turn angular rate estimation and subtraction are used in the yaw axis to improve the directional damping.Besides,feedforward control is adopted to improve the maneuverability and control decoupling performance. Then, detailed design methods for feedback and feedforward control parameters are established using eigenstructure assignment and model following technique. Finally, the proposed design method is evaluated and compared with conventional method by numeric simulations.The influences of control derivatives variation of drag rudders on the method are also analyzed.It is demonstrated that the method can effectively improve the dynamic characteristics of flying wing aircraft, especially the directional damping characteristics, and decouple the longitudinal responses from the drag rudders.

1. Introduction

Flying wing aircraft lacks vertical and horizontal tails, which leads to weak instability of the directional axis and degraded longitudinal and lateral stability compared with conventional aircraft. As a result, the modal characteristics of flying wing aircraft cannot satisfy the aircraft flying quality requirements.In addition,flying wing aircraft is typically equipped with multiple sets of elevons and drag rudders to satisfy control power demands for maneuverability.1-3However, drag rudders have strong three-axis aerodynamic forces and moment coupling during deflection; the coupling will further degrade the flying quality of flying wing aircraft.4-8Therefore, it is necessary to adopt an advanced flight control law to ensure that flying wing aircraft exhibits excellent flying qualities and becomes truly controllable aircraft.

Many studies have been conducted on the application of modern flight control design methods to flying wing aircraft.Christian et al. designed an attitude tracking control law for flying wing aircraft with sliding-mode control.9Andrew designed an automatic gain scheduling flight control law for flying wing aircraft using the Linear Parameter-Varying(LPV) method.10Anhtuan et al. designed a longitudinal and lateral-directional decoupled control law for a flying wing fighter based on the μ synthesis method.11Rowena et al.obtained a stability augmentation control law for ICE aircraft via the model predictive control method.12However,the above works did not strictly consider the aircraft flying quality specifications and the longitudinal and lateral-directional control coupling that is caused by drag rudder deflection; hence, the flying qualities and the dynamic decoupling performance of flying wing aircraft cannot be guaranteed.

Flying-quality-based flight control law design is a trend in the development of flight control.13-15The Eigenstructure Assignment (EA) design method could effectively integrate the requirements of flying quality specifications and dynamic decoupling into the control structure and the controller parameter design procedure,which is highly desirable for engineering applications. For conventional aircraft, the EA method is mainly used for lateral-directional control law design to realize dynamic decoupling and satisfactory flying qualities,while the longitudinal control law is typically designed via the PID method.16-21Refs.22-28adopted the Control Augmentation System (CAS) design method for conventional aircraft and conducted a series of studies on flight control law design for flying wing aircraft. The results have demonstrated the satisfactory performance of EA method.However,the main drawback of the CAS design method that is described above is that lateral-longitudinal decoupled design cannot deal with the longitudinal-directional control response coupling that is induced by the drag rudder.

In addition,in the lateral-directional CAS structure,a highpass filter is often used in the directional feedback channel to filter the steady-state yaw rate,thereby avoiding the generation of unnecessary rudder deflection during maneuvering turns.Nevertheless, the Dutch roll modal frequency of flying wing aircraft is low due to the elimination of vertical tails. If a high-pass filter is used in the directional feedback path of a flying wing aircraft, the effective feedback yaw rate will be partially filtered, which will result in insufficient directional damping and will degrade the flying qualities of the closedloop aircraft.29

Aimed at overcoming the poor Dutch roll modal characteristics and the control coupling of the drag rudder,a longitudinal and lateral-directional axes coupled flight control law design method for flying wing aircraft is proposed. First, a three-axis coupled control augmentation structure is established based on the three-axis coupled dynamics of flying wing aircraft. In the structure, ‘‘soft/hard” cross-connection design is adopted for three-axis dynamic decoupling and longitudinal control response decoupling from the drag rudder.In addition,maneuvering turn angular rate estimation and subtraction are used in the directional feedback channel instead of a high-pass filter to improve the damping characteristics of the Dutch roll mode.To improve the maneuverability and control the decoupling effect of the aircraft, a feedforward control path is also introduced in the control structure. Second, a detailed control parameter design method for the three-axis coupled flight control law is developed. The feedback and feedforward control parameters are designed via the EA and model following techniques, which will guarantee that the control parameters satisfy the requirements on the flying qualities and the dynamic decoupling. Finally, a three-axis coupled control law design example is presented using a flying wing aircraft.The accuracy and effectiveness of the proposed method are evaluated via flying quality evaluation and closed-loop maneuver command tracking, and the influences of control derivatives variation of drag rudders on the control law are analyzed by perturbed simulation.

The remainder of this paper is organized as follows,Section 2 introduces the three-axis coupled flight control law design method in detail.A control design example for the proposed method is presented in Section 3. Section 4 presents the results of the flying quality evaluation, the control decoupling effects and the performance variation of the design method under control derivatives perturbation of drag rudders. Section 5 presents the conclusions of the paper and summarizes the advantages of the proposed method.

2. Three-axis coupled flight control law design

2.1. Three-axis coupled control augmentation structure design

The short-period modal characteristics of flying wing aircraft are poor due to the elimination of horizontal tails. The safety flight Angle of Attack(AOA)is small after the adoption of the all-wing design.2Therefore,the pitch axis control law for flying wing shall use the AOA command structure, which can improve the short-period modal characteristics and impose strict operation restrictions on AOA. Due to the lack of vertical tails,the Dutch roll modal characteristics of the flying wing are degraded and the lateral-directional dynamic coupling is strong.Hence,the lateral-directional control law should adopt the combination of roll angle variation rate and sideslip angle command structure. The advised control command structure can improve the Dutch roll modal characteristics, alleviate the dynamic coupling of the lateral-directional axes and ensure that the aircraft has satisfactory lateral-directional control response characteristics.

For the redundant multicontrol surfaces of flying wing aircraft,it is necessary to preallocate the functions of control surfaces prior to designing the flight control law. In practical applications, the functions of control surfaces are manually decoupled, drag rudders are designated for yaw control,inboard elevons are used for pitch control and outboard elevons are used for roll control. In the following text, δa, δeand δrwill be used to represent three-axis equivalent control surfaces such as conventional aircraft.

The conventional CAS design method assumes that the longitudinal and lateral-directional dynamics of aircraft are decoupled; hence, the longitudinal CAS and the lateral CAS can be designed separately.13,30However, the separated longitudinal and lateral-directional control structure cannot consider the control disturbance of the drag rudders to the longitudinal axis and it is difficult to obtain satisfactory three-axis control decoupling performance.

Therefore, this paper proposes a three-axis coupled CAS design methodology for flying wing aircraft and attempts to improve the dynamic characteristics of flying wing aircraft,to decouple the longitudinal control response from the drag rudder and to realize satisfactory maneuvering flight performance simultaneously.

Fig. 1 illustrates the three-axis coupled control augmentation structure. Where α is the angle of attack; β is the sideslip angle; ˙φ is the roll angle variation rate;p，q，r are the body-axis angular rates; δa，δe，δrrepresent the control inputs of roll,pitch and yaw axis; αcmd，βcmd， ˙φcmdare the command inputs;K and Kfare the feedback and feedforward control parameters.

The three-axis coupled control augmentation structure consists of five main components, the yaw rate ‘‘washout” unit,the control surface decoupling unit, the feedback control augmentation loop,the maneuvering command tracking loop,and the command feedforward path.The yaw rate‘‘washout”unit is mainly used to improve the damping characteristics of the Dutch roll mode. Maneuvering turn angular rate estimation and subtraction are used instead of high-pass filtering to increase the effective feedback yaw rate. The control surface decoupling unit can decouple the longitudinal control response from the drag rudder by directly connecting the drag rudder with the elevons that are dedicated for pitch control.The feedback stabilization loop is mainly used to improve the modal characteristics of flying wing aircraft and to realize the decoupling of the three-axis dynamics. Integrator states are introduced in the maneuvering command tracking loop to ensure accurate tracking of the maneuvering command. The lateraldirectional states are fed back into the longitudinal channel via the command tracking loop,which can improve the control decoupling performance of the drag rudder. The command feedforward path is used to appropriately shape the maneuvering command to improve the command response speed of the aircraft. Since the lateral and directional maneuvering commands enter the longitudinal axis through the feedforward path, the longitudinal steady-state response will be decoupled from lateral-directional commands.

2.2. Alternative method to ‘‘wash out” the feedback yaw rate in directional channel

Due to the low frequency of the Dutch roll mode and the lower control effectiveness of the drag rudder compared to a conventional rudder,7the yaw axis of a flying wing aircraft requires higher strength feedback signals. If a high-pass filter is used on the yaw axis of the flying wing to filter the steady-state rate during a maneuvering turn, it will cause partial feedback yaw rate loss, thereby resulting in a substantial decrease in the directional damping. To demonstrate the adverse effect of a high-pass filter,Fig.2 compares the sideslip angle β command tracking performance of a flying wing aircraft with and without a high-pass filter on the yaw axis.

The high-pass filter substantially reduces the directional damping during maneuvering and, consequently, the flying quality is degraded.

Various large transport aircraft with low Dutch roll frequency estimate the maneuvering turn angular rate and subtract it from the yaw axis in real time instead of using a high-pass filter.29For flying wing aircraft, this method can be used to avoid the adverse effects of the high-pass filter on flying quality.The method that is used to estimate the maneuvering turn angular rate and the instantaneous roll, pitch and yaw rates is expressed in

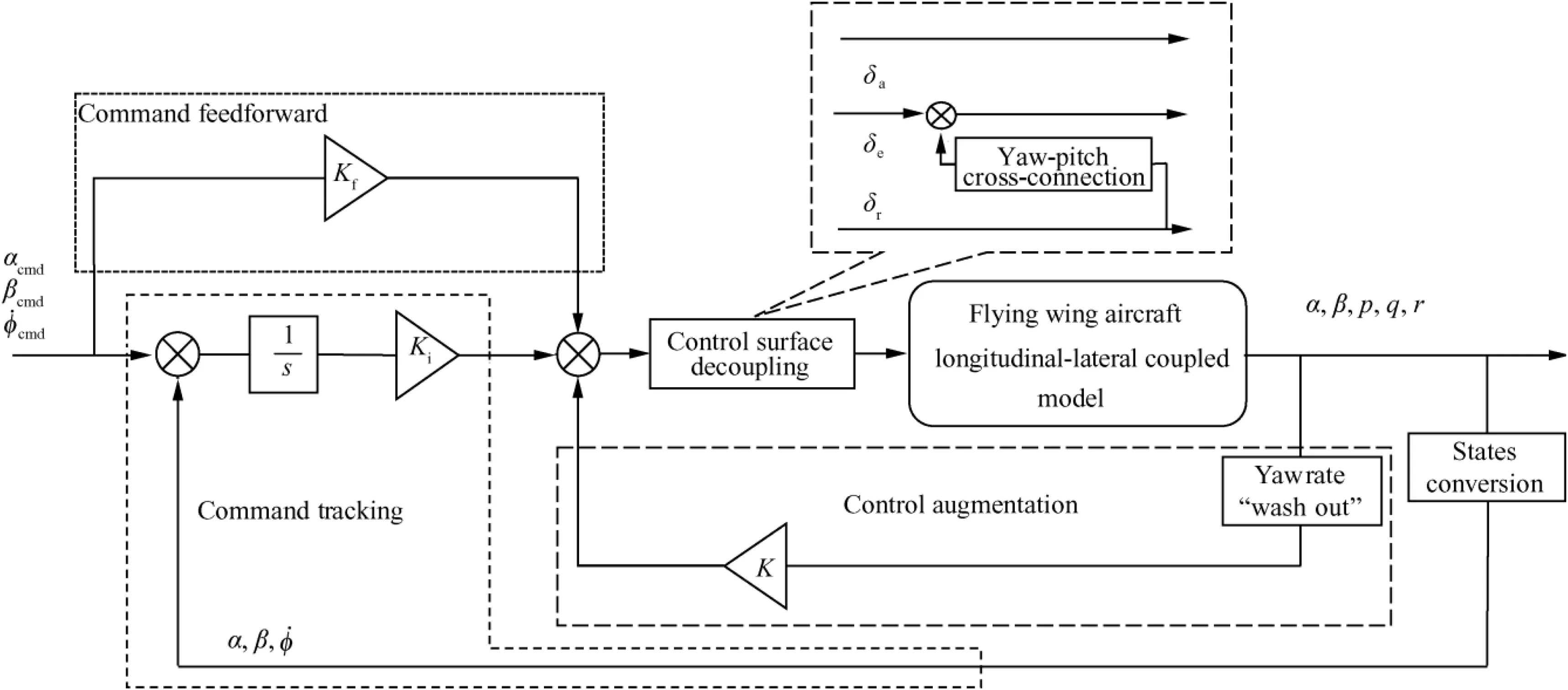
Fig. 1 Three-axis coupled control augmentation structure of flying wing aircraft.

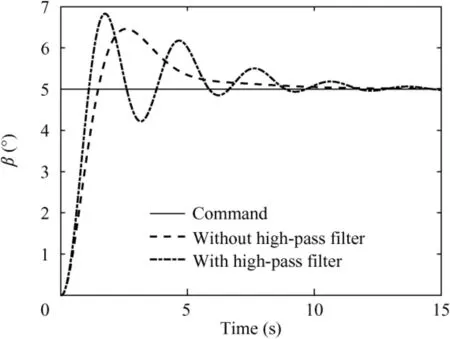
Fig. 2 Comparison of influence of a high-pass filter on a directional maneuver.

where Ωcis the maneuvering turn rate; nzrepresents the normal load; g is the acceleration of gravity; V is the airspeed; θ is the pitch angle;φ is the roll angle;p，q，r are three-axis angular rates that are measured by an Inertial Measurement Unit(IMU) in the instantaneous turning state; pf，qf，rfare the three-axis feedback angular rate signals after the steady-state angular rate components have been subtracted.

2.3. Dynamic responses decoupling based on ‘‘soft/hard” crossconnections

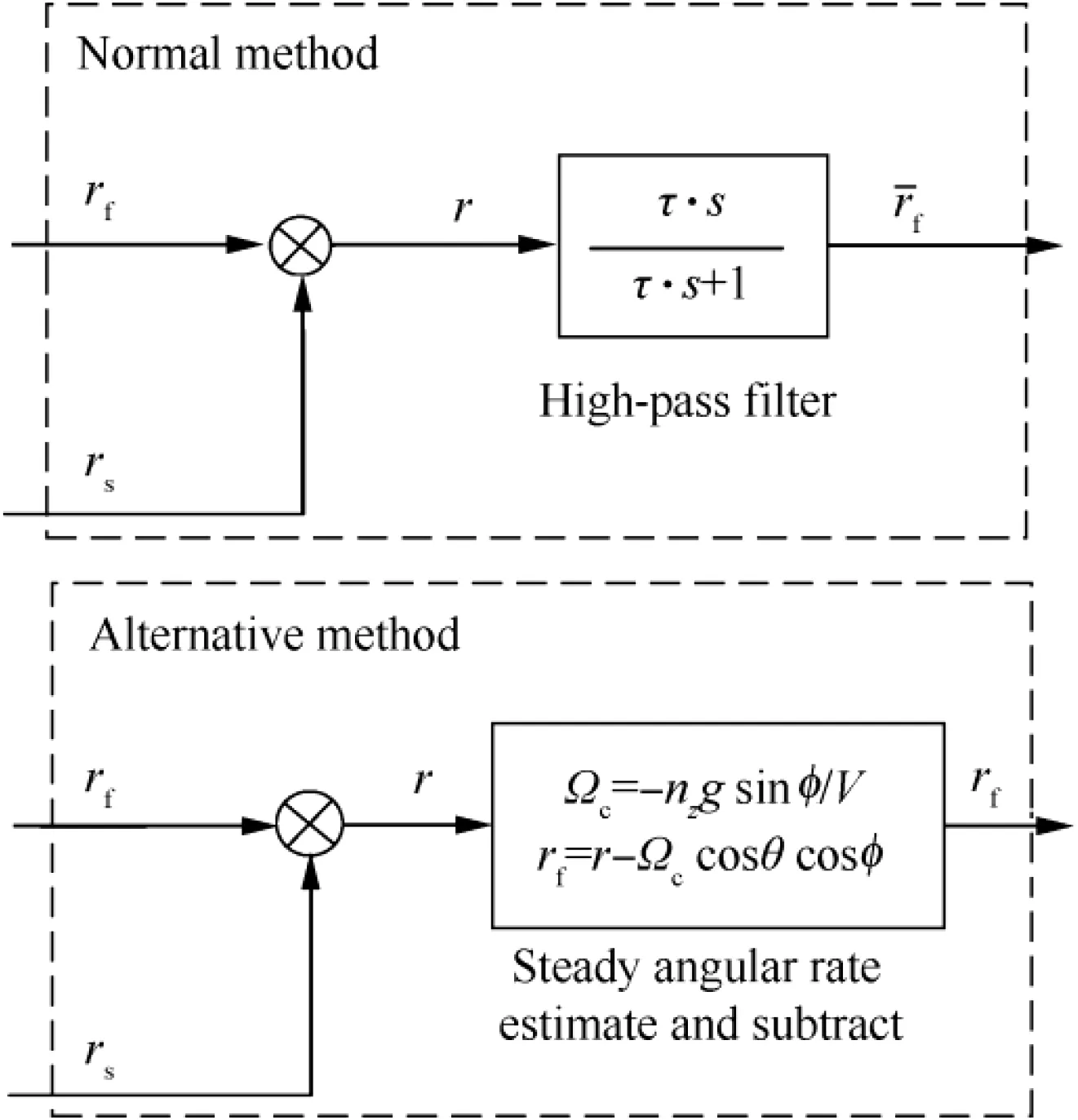
Fig.3 Comparison of yaw feedback signals for two angular rate filtering methods.

Conventional aircraft often uses the ‘‘soft/hard” crossconnection control method to realize satisfactory dynamic decoupling performance.13,30A ‘‘soft” cross-connection refers to the feedback of the output signal from a channel of the aircraft to another channel to realize dynamic decoupling or coordinated control.In a‘‘hard”cross-connection,the control surface command of a channel is fed into the control surfaces of another channel directly.Since the‘‘hard”cross-connection method will connect related control surfaces directly,it has faster control response speed than ‘‘soft” cross-connection; however, the control command from ‘‘hard” cross-connection is typically not sufficiently smooth. The two cross-connection control methods can be used separately or simultaneously to ensure the decoupling of the aircraft dynamics.

To solve the three-axis dynamic coupling problem of flying wing aircraft that is caused by the drag rudder,a‘‘soft”crossconnection design is used to decouple the dynamics of the pitch, roll and yaw axes. Then the drag rudders are ‘‘hard”cross-connected to inboard elevons to realize longitudinal and directional control decoupling. The three-axis dynamic decoupling theory that is based on the cross-connection method is illustrated in Fig.4,where G（δa）represents the control relationship of the outboard elevons with the roll angle variation rate, G（δr） represents the relationship of the drag rudder deflection with the sideslip angle, G（δe） represents the pitch control relationship of the inboard elevons with AOA,F1represents the coupling relationship of the yaw axis with the roll angle variation rate, F2represents the coupling relationship of the roll axis with the sideslip angle, and F3represents the coupling relationship of the yaw axis with AOA.The lateral and directional control coupling that is induced by the drag rudder can be decoupled by introducing negative G1,G2and G3feedbacks on the yaw,roll and pitch axes,while the directional and longitudinal axes mainly use‘‘hard”crossconnection G4to eliminate the control coupling.

EA is used to design the‘‘soft”cross-connection decoupling parameters, namely, G1, G2and G3. And the detailed design routine of EA method will be described in the next section.

The yaw-pitch ‘‘hard” cross-connection decoupling parameter, namely G4, can be solved based on the following relationship

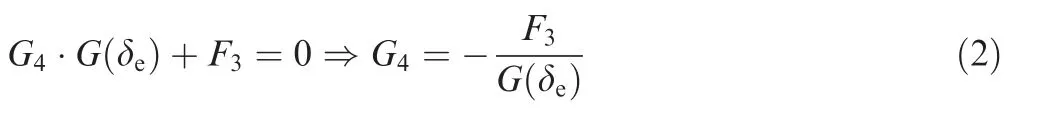
2.4. EA-based three-axis coupled control design

For conventional aircraft, the EA method is typically used to design lateral-directional CAS to improve the modal characteristics and realize satisfactory control decoupling performance of the roll-yaw axes. For flying wing aircraft, to overcome the problem of three-axis dynamic coupling that is caused by the drag rudder, this paper proposes a three-axis coupled EA design method for decoupling the aircraft’s control responses from the drag rudder.

When designing actual flight control systems, the requirements for state feedback design are typically difficult to satisfy.Thus, the output feedback EA method is used to design the feedback control parameters for the three-axis coupled flight control law. The related theory and detailed design routine of the method can be found in Ref. 31. The following figure illustrates the procedure for designing a three-axis coupled control law via the EA method.

According to the design procedure in Fig. 5, prior to designing the control parameters for flying wing aircraft, the command tracking integrators in Fig.1 and three-axis coupled dynamic model must jointly establish an augmented state space model for the aircraft.

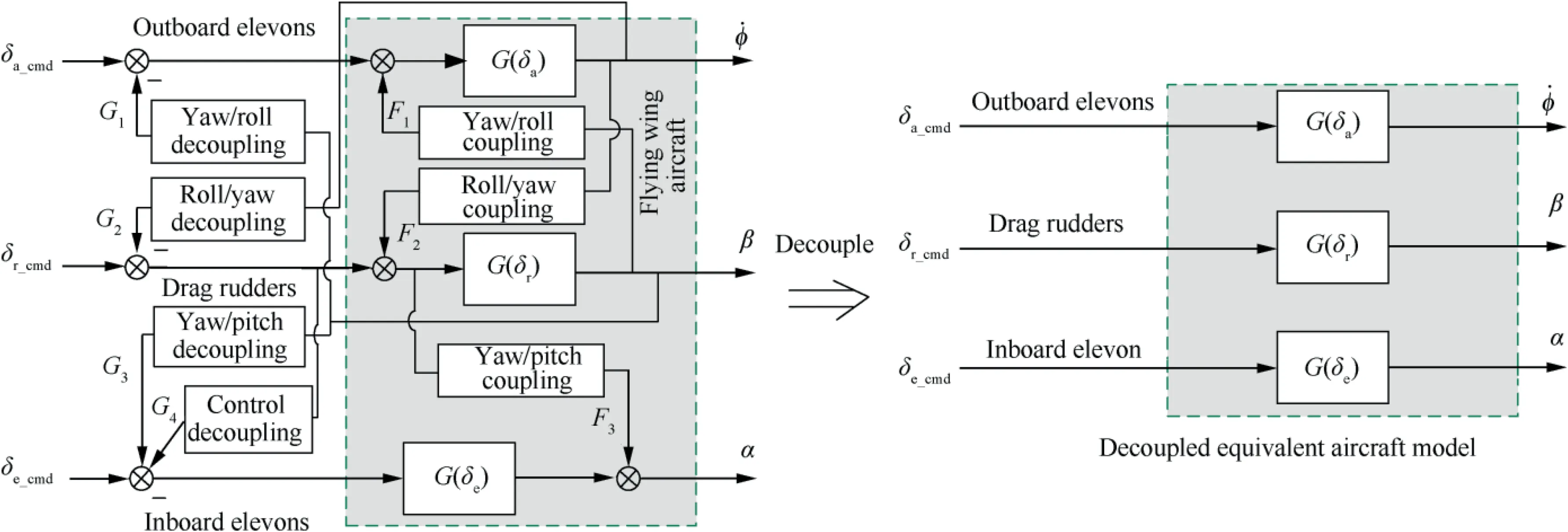
Fig. 4 Dynamic decoupling theory of flying wing aircraft.

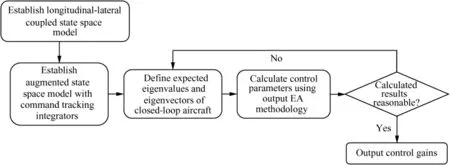
Fig. 5 Three-axis coupled EA design procedure.

First, according to the three-axis coupled control augmentation structure of the flying wing aircraft, the AOA, sideslip angle,roll rate,pitch rate and yaw rate are selected as the state variables and the three-axis control variables are selected as δa,δeand δr,which represent inboard elevons for roll control,outboard elevons for pitch control and the drag rudders for yaw control, respectively. Then, the fifth-order linear dynamic model that combines the longitudinal and lateral-directional axes is established in matrix form

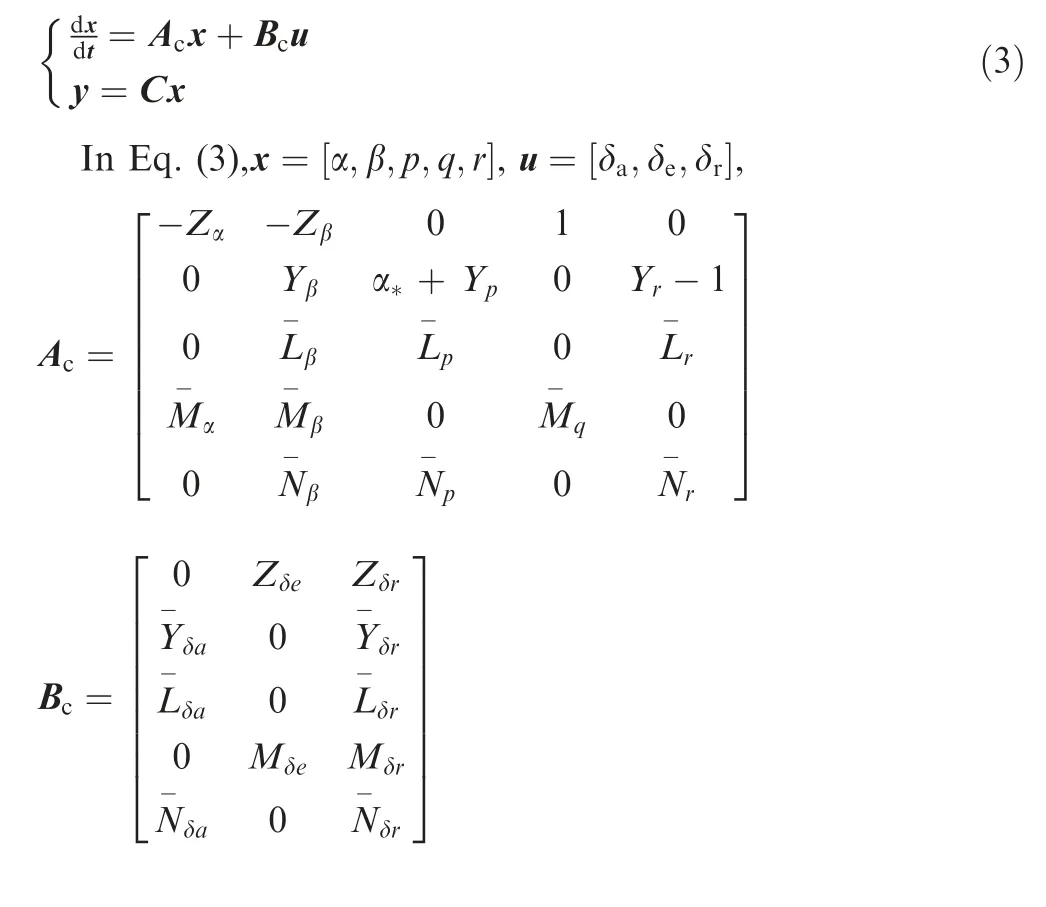
Detailed expressions of the derivative terms in the coupled model can be found in Ref.13 or Ref.30.In system matrix Ac,the longitudinal and lateral-directional coupled force Zβand moment M-βthat are induced by sideslip angle change under small AOA are considered.8The derivative terms Zδr, Y-δr,Mδrand L-δrin the control effectiveness matrix Bcare additional aerodynamic force and moment control derivatives that are induced by the drag rudders.

Based on the coupled dynamic model, the augmented aircraft state space model is established as follows:

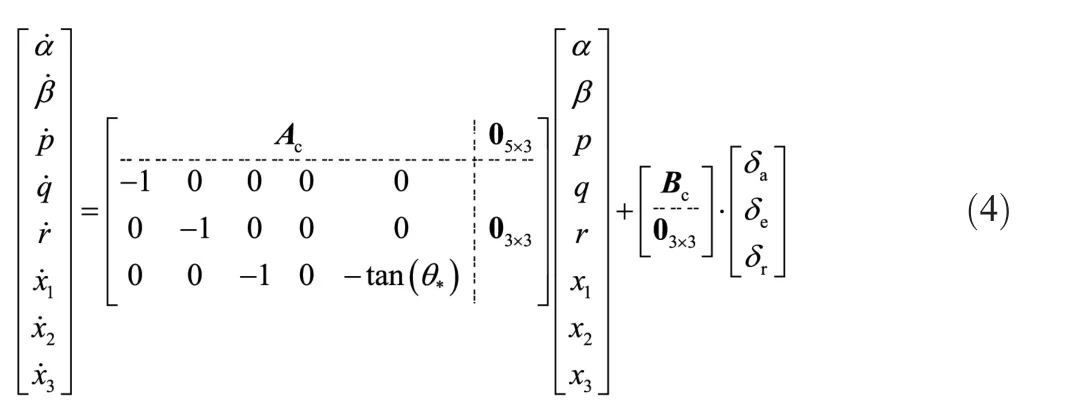
where θ*represents the pitch attitude of the aircraft at trimmed wing level flight, x1，x2，x3represent the command tracking integrator states for the AOA, sideslip angle, and roll angle variation rate, respectively.

Since new integrator states are introduced into the augmented longitudinal and lateral-directional coupled model,the output matrix Ccof the coupled model must also be expanded

According to the modal characteristics requirements for longitudinal and lateral-directional axes that are specified in aircraft flying quality specifications32and the three-axis coupled control law structure, the eigenvalues that must be assigned in the closed-loop aircraft system are the shortperiod mode,the roll mode,the Dutch roll mode,and the longitudinal and lateral-directional three-axis command tracking integrators. Due to the integrator in the forward path of the roll axis command structure, the closed-loop aircraft system always has a zero eigenvalue that corresponds to the spiral mode; hence, the spiral mode is neutrally stable.

To realize three-axis dynamic decoupling and control decoupling on the drag rudders, the eigenvectors of the closed-loop aircraft system should be assigned properly.The three-axis dynamic decoupling design needs to properly assign the corresponding eigenvectors of the longitudinal and lateral-directional states. The control decoupling design is mainly used to reduce the adverse interference of the drag rudder deflection on the roll and pitch axes when performing a maneuvering task. It can be realized by assigning the eigenvectors that correspond to the eigenvalues of the command tracking integrators. Therefore, the desired eigenvector structure Vdthat satisfies the decoupling requirements is as follows

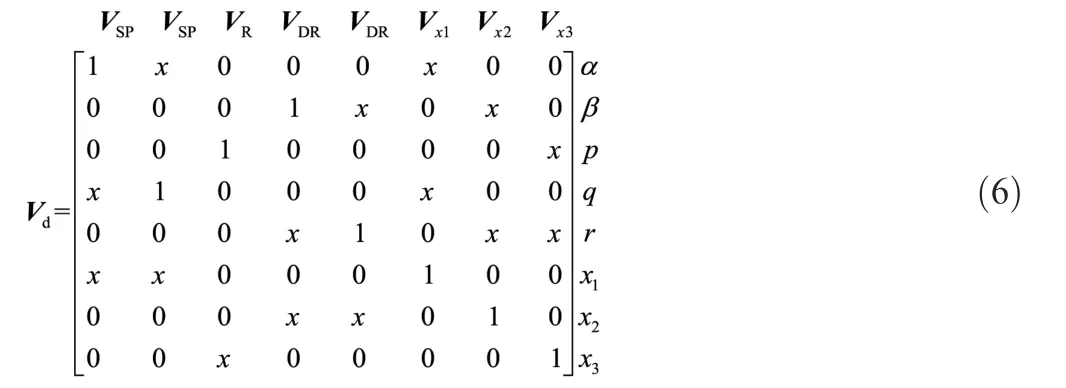
where ‘‘x” represents an eigenvector element that is not of interest and ‘‘0′′and ”1′′represent the state elements that are designed according to modal decoupling requirements; VSP,VRand VDRrepresents the desired eigenvectors of the shortperiod mode, the roll subsidence mode, and the Dutch roll mode, respectively; Vx1, Vx2and Vx3are the desired eigenvectors that correspond to the integrator eigenvalues of the pitch,yaw and roll axes.

In the three-axis coupled control augmentation structure,due to the elimination of the high-pass filter in the yaw axis,the output variables of the aircraft system are consistent with the state variables. Thus, the output feedback EA method can accurately assign all the closed-loop system eigenvalues.Although the assigned closed-loop system eigenvectors usually have minor differences from the expected eigenvectors, the coupling degrees of closed-loop aircraft can be substantially reduced.31

2.5. Command enhancement and feedforward decoupling design based on model following

After adopting the EA design, the control response speed of closed-loop aircraft to maneuvering commands remains slow.However, the response speed can be improved by adding a command feedforward compensator to properly shape the control input,while the stability of the closed-loop aircraft system is not affected. For the three-axis control coupling effect of the drag rudder, a cross feedforward design of the yawpitch axis and the yaw-roll axis can be used to realize input decoupling of three-axis control commands and to reduce the handling disturbance of the drag rudder. When designing the feedforward compensator, the closed-loop aircraft system structure that is illustrated in Fig. 6 should be used.

In Fig. 6, A, B and C are the longitudinal and lateraldirectional coupled dynamic model matrices of the flying wing aircraft;H is the observer matrix for the aircraft states that are expected to be tracked; umrepresents the reference input commands; x represents the aircraft states; u denotes the control inputs;y denotes the measurable outputs;z denotes the aircraft responses that are expected to be tracked;Kfis the feedforward compensator; K is the control gain of the feedback augmentation loop,which is illustrated in Fig.1 and is calculated via the output feedback EA method.

To calculate the feedforward compensator Kf, assume that the ideal aircraft state space model with desired dynamic characteristics is

where Am, Bm, Cmand Dmare state-space matrices for the ideal aircraft model, xmrepresents the states of the ideal model, and ymdenotes the outputs of the ideal model. The state variables and control variables of the controlled aircraft system can be represented by ideal models and error vectors

In Eq.(8),δx is the state error vector;δu is the control input error vector; the relationship between the control input error vector and the state error vector is δu=KCδx; S11, S12, S21and S22are unknowns that need to be solved. Via proper derivation,33we obtain the following

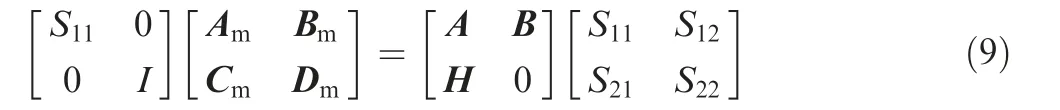
For general aircraft dynamic equations, the matrix that consists of A, B and H in Eq. (9) is typically nonsingular and its inverse matrix can be partitioned as

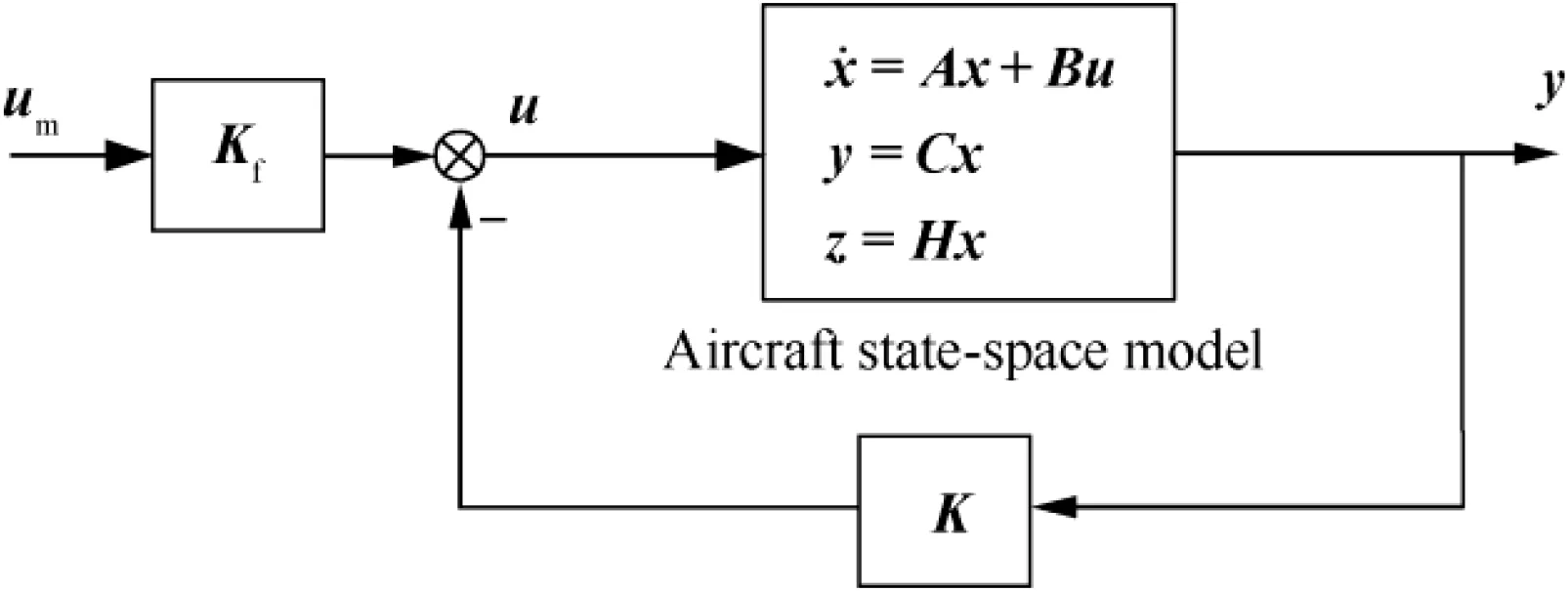
Fig. 6 Feedforward control structure.

where Ω represents the inverse of the matrix that consists of A,B and H, and Ω11, Ω12, Ω21and Ω22are the partitioned submatrices of Ω. To simplify the calculation, assume that the feedforward compensator Kfis pure gain and that the outputs ymof the ideal model can track command input signals umdirectly. Then, the ideal state space model can be set to

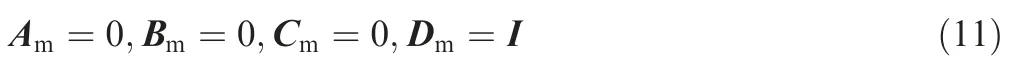
Substituting Eqs. (10) and (11) into Eq. (9) yields the following values of S11, S12, S21and S22

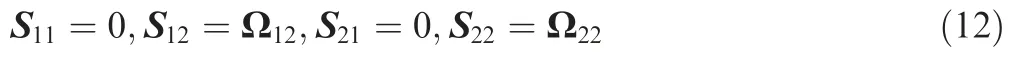
Substituting the result in Eq. (12) into Eq. (8) yields the control inputu

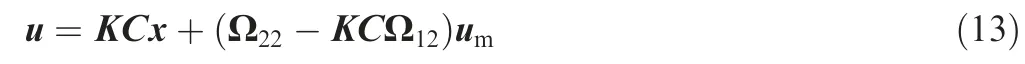
In Eq. (13), the control input u of the aircraft consists of two parts,the former part represents the output feedback from the control system and the latter part represents the shaping of the command input signal from the feedforward gain matrix.Thus, the feedforward gain Kfcan be expressed as

3. Three-axis coupled control law design example

To evaluate the performance of the three-axis coupled flight control law design method, a three-axis coupled CAS is designed for an example flying wing aircraft,the flying quality and the control decoupling effect of the closed-loop aircraft are evaluated, and the influences of control derivatives variation of drag rudders on the three-axis coupled control law are analyzed by parameter perturbed simulation.

3.1. Dynamic characteristic analysis of example aircraft

The example flying wing aircraft is illustrated in Fig. 7. It is equipped with two sets of elevons and a set of split drag rudders. The control functions of the control surfaces are allocated via manual decoupling, the inboard elevons are mainly used for pitch control, and symmetric downward deflection is defined as positive deflection;the outboard elevons are used for roll control via differential deflecting,and deflection of the left elevon upward and of the right elevon downward is defined as positive deflection. The split drag rudders are dedicated for yaw control, with the open left side control surface defined as positive deflection.

Considering typical flight condition (Ma=0.5 and H=5 km) as an example, the static stability derivatives and typical dynamic modes of the aircraft are listed in Table 1.Where Cmαis the longitudinal static stability derivative, Clβis the lateral static stability derivative,Cnβis the directional static stability derivative.

According to Table 1, the example aircraft is longitudinal unstable, due to the lack of vertical tails, the yaw axis of the example aircraft exhibits typical weak static instability characteristics of the flying wing,and the static stability of the lateral axis is reduced compared to conventional aircraft.

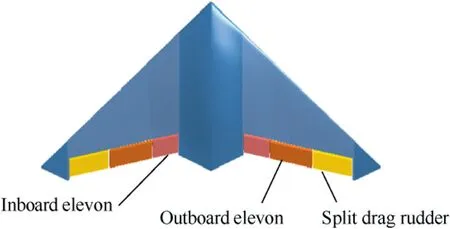
Fig. 7 Control surface configurations of example flying wing aircraft.

Table 1 Typical static stability derivatives.

Under the typical flight condition, the longitudinal and lateral-directional coupled dynamic model is shown in Eq.(15), and when the sideslip angle changes, it will perturb the longitudinal dynamic and cause longitudinal and lateraldirectional dynamic coupling. The typical dynamic modes of the example aircraft are given in Table 2.

The dynamic modes in Table 2 demonstrate that the shortperiod mode of the example aircraft is unstable, whereas the roll mode characteristics are relatively satisfactory and the Dutch roll mode is dynamically unstable.Therefore,the design of CAS must focus on improving the short-period mode and the Dutch roll mode characteristics of the example aircraft to satisfy the flying quality specifications.

The split drag rudders of flying wing aircraft will produce strong three-axis coupling of forces and moments during deflection, and the strong coupling characteristics have been thoroughly analyzed in Ref. 7. Fig. 8 plots the three-axis moment control coefficients of the split drag rudders for the example aircraft under typical flight condition.

According to Fig.8,as the drag rudder deflection increases,the coupling control coefficients of the pitch and roll axes become significant. When the split drag rudder deflects positively, it generates a negative roll moment coefficient; hence,the aircraft tends to roll off to the split rudder opened side,and regardless of whether the split rudder is deflecting positively or negatively, it generates a positive pitching moment coefficient, which indicates that the aircraft tends to pitch up.Although the absolute values of the roll and pitch momentcoefficients that are generated by the split rudder are small, it still has a substantial impact on the roll and pitch dynamics during cruising flight and degrades the flying quality of the aircraft.

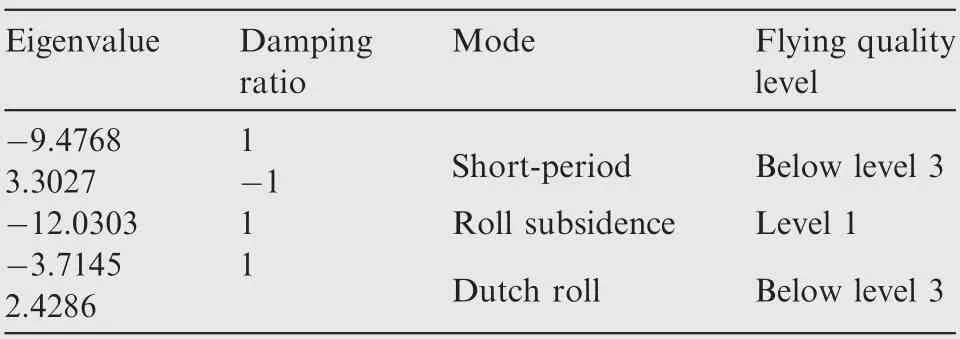
Table 2 Typical dynamic modes.

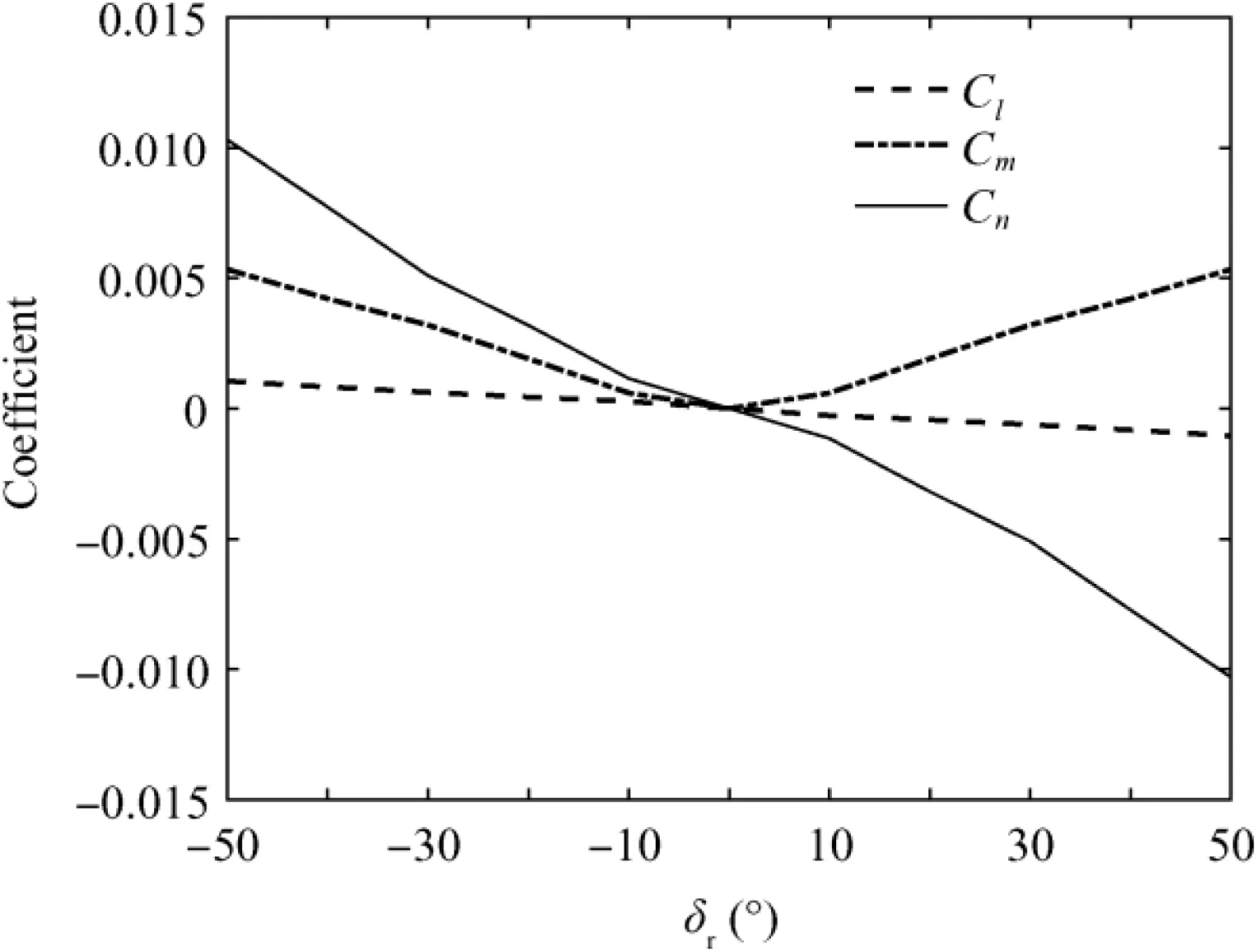
Fig. 8 Moment control coefficients of split rudder.

3.2. Control law parameter design

3.2.1. Decoupling parameters of ‘‘hard” cross-connections

According to the decoupling method of the drag rudder that is presented in Section 2.3, the yaw-pitch axis adopts a ‘‘hard”cross-connection design. The cross-connection parameter Kr2eis calculated as:

The derivative term Mδrin Eq. (16) is the pitch moment derivative that is induced by the drag rudder, which varies nonlinearly with the AOA and the drag rudder deflection.

Table 3 Desired eigenvalues of closed-loop aircraft.

Therefore, the ‘‘hard” cross-connection decoupling parameter must use the gain scheduling design in practical applications.

3.2.2. Control parameters for ‘‘soft” cross-connection decoupling, stabilization and command tracking

The desired eigenvalues of closed-loop aircraft are listed in Table 3, which are determined based on the aircraft flying quality specifications for the category B phase.32The integrator eigenvalues of the pitch, roll and yaw axes are assigned according to Ref. 34. The desired eigenvectors of closed-loop aircraft are consistent with Eq. (6).

The closed-loop aircraft eigenvectors VA, the ‘‘soft” crossconnection decoupling and stabilization control gain K and the command tracking gain Kiare obtained via the three-axis coupled EA design method and are expressed as follows,

By analyzing the control gain K,it is observed that the sideslip angle and the yaw rate are fed back into the roll axis to realize yaw-roll axis ‘‘soft” cross-connection decoupling. Further analysis of the control gains K and Kireveals that some lateral-directional states of the aircraft, such as the sideslip angle and the yaw rate, are fed back into the pitch axis; in the command tracking path, the error integrals of the sideslip angle and the roll angle variation rate are also fed back into the pitch axis. Since these lateral state variables are fed back into the longitudinal channel of the aircraft, when drag rudders deflect and cause changes in the lateral-directional states,the inboard elevons can actively deflect to reduce the adverse interference of the drag rudders with longitudinal motion and to realize superior aircraft dynamic decoupling performance.

3.2.3. Feedforward control parameters

For the example aircraft, using model following method described in Section 2.5 and the calculated feedback control gain K, the feedforward gain is calculated as

The feedforward gain Kfof the example aircraft is a 3×3 matrix. According to an analysis of the matrix elements, the yaw-roll axis of the closed-loop aircraft has a cross feedforward relationship, which ensures yaw or roll steady-state response decoupling from the roll or yaw command inputs.The roll and yaw maneuvering commands are fed forward into the pitch axis, and thus, when performing yaw or roll maneuvers,the pitch steady-state response will be decoupled from the yaw or roll maneuver command and the interference of the drag rudder control coupling with the longitudinal motion will be reduced.

If the response characteristics of the closed-loop aircraft are unsatisfactory after the addition of the forward proportional gain, the gain values can be adjusted to satisfy the accuracy requirements for command tracking.

4. Flying quality evaluation and numerical simulation verification

4.1. Flying quality evaluation

For the flying quality evaluation of high-order closed-loop aircraft, the Low-Order Equivalent System (LOES) matching method is recommended in aircraft flying quality specifications for conventional aircraft.35However,due to the non-negligible differences in the stability and control characteristics between flying wing aircraft and conventional aircraft, the LOES matching method for conventional aircraft is not fully applicable to flying wing aircraft. Therefore, the improved LOES matching method for flying wing aircraft in Ref. 36 is used to perform the flying quality evaluation of the example aircraft.

The CAS for example aircraft is designed via the three-axis coupled control design method, which mainly focuses on improving the insufficient directional damping of flying wing aircraft. To compare the three-axis coupled control design method and the conventional lateral-longitudinal decoupled design method (which are hereinafter referred to as the ‘‘coupled method” and the ‘‘normal method”) in terms of performance in improving the flying quality of flying wing aircraft,a standalone lateral-directional CAS is designed for the example aircraft using the lateral-directional control augmentation structure of conventional aircraft13and the same control design objectives as the ‘‘coupled method”.

Under a typical flight state (Ma=0.5 and H=5 km) and using the improved LOES matching method, the lateraldirectional and longitudinal LOES models of the example aircraft for the ‘‘coupled method” are obtained, as presented in Tables 4 and 5. For comparison, the lateral-directional LOES models for the‘‘normal method”are also presented in Table 4.

According to the lateral-directional LOES models in Table 4,the flying quality evaluation results for the two design methods are calculated and listed in Table 6.According to the results, both of the design methods can ensure that the example aircraft satisfies the requirements of Level 1 flying quality.In the evaluation results,the differences in the roll modal characteristics are minor; however, under the same control law design objective, the Dutch roll modal damping for the ‘‘normal method”is only 0.47,whereas for the‘‘coupling method”,the damping is improved to 0.61,which represents an increase of approximately 30%.In addition,the Dutch roll mode eigenvalues of the closed-loop aircraft are closer to the design objectives than those of the ‘‘normal method”.

According to longitudinal LOES models in Table 5, the evaluation parameters of the Control Anticipation Parameter(CAP) criterion are calculated, which are listed in Table 7.The evaluation results demonstrate that the equivalent CAP parameters and the equivalent short-period modal characteristics of the closed-loop aircraft satisfy the level 1 flight quality requirements.

In conclusion,the CAS that was designed via the‘‘coupled method” can ensure that the three axes of flying wing aircraft satisfy the level 1 flying quality requirements and the directional damping characteristics can be substantially improved.Meanwhile, the ‘‘coupled method” assigns the closed-loop eigenvalues more accurately,which avoids the subsequent iterative design of the ‘‘normal method”.

4.2. Evaluation of control decoupling performance

Currently, there is no quantitative standard in the aircraft flying quality specifications for evaluating the decoupling performance of the drag rudder. Thus, a closed-loop command tracking simulation is used to evaluate the control decoupling performance of the proposed method and the differences in the aircraft maneuvering response characteristics under the CASs that were designed via the two methods are compared and analyzed. Since the control coupling is mainly generated by the deflection of the drag rudder, the following text will focus on analyzing the decoupling performance of the ‘‘coupled method” in yaw maneuver and coordinated turn maneuver simulations.

4.2.1. Yaw axis maneuvering command tracking

Under the cruise state of Ma=0.5 and H=5 km, using the CASs that were designed via the above two methods,the state responses of the example aircraft tracking β=3◦step command and the variations of three-axis control surface deflection are plotted in Fig. 9.

Fig. 9(a) shows that both of the design methods realize accurate tracking of the sideslip angle command. According to Fig. 9(b), when using the ‘‘normal method”, the tracking sideslip angle command generates an AOA disturbance with a maximum amplitude of approximately 0.5°and slow convergence,whereas for the”coupled method‘‘,the disturbed ampli-tude of AOA is less than 0.1° and the disturbance converges quickly.These differences can be well explained by the control surface deflection that is presented in Fig. 9(c), (d). At the initial stage of the simulation,when using the”coupled method‘‘,the sideslip angle command enters the inboard elevons through the feedforward channel, which alleviates the initial tendency of AOA increasing. As the deflection of the drag rudder continues to increase, the inboard elevons deflect in coordination with the drag rudders since they are directly ‘‘hard” crossconnected; therefore, the pitch control disturbance from the drag rudder is effectively suppressed and the variation of AOA is small.

Table 4 Lateral-directional LOES results.

Table 5 Longitudinal LOES result.

According to the numerical simulation results that are presented above, by using the three-axis coupled design method,the pitch and yaw axes of the aircraft can better control the decoupling effects during a yaw maneuver.

4.2.2. Coordinated turn simulation

To further evaluate the dynamic decoupling and maneuver decoupling performance of the ‘‘coupled method”, a coordinated turn maneuver is used to evaluate the proposed method.The baseline flight state and CASs are the same as in the previous section.At the initial time of the simulation,the example aircraft is in steady wing level flight and a square wave command with amplitude ˙φ=18（◦）/s and width 3 s is applied to the roll axis, while the pitch and yaw axes maintain trimmed inputs. The simulation results of the two methods are plotted in Fig. 10.

Fig. 10(a) shows that using the CASs that are designed by the two methods can guarantee accurate tracking of the roll angle variation rate command. In Fig. 10(c), when using the‘‘normal method”,the convergence speed of the disturbed sideslip angle is substantially lower than that of the ‘‘coupled method”. The discrepancy is illustrated by the yaw rate comparison of the two methods in Fig.10(f).When using the‘‘coupled method”,the effective feedback yaw rate signal strength is increased due to the cancellation of the directional high-pass filter; hence, the directional damping characteristic is improved.As a result,the oscillatory amplitude of the yaw rate is reduced and the convergence rate of the disturbed sideslip angle is increased.

During coordinated turn maneuvering, since the command amplitude of the roll angle variation rate is large, the coordinated deflection of the drag rudder is also large, as shown in Fig.10(i).According to Fig.10(b),when the‘‘normal method”is used,the control disturbance from the drag rudder induces a long-time AOA oscillation motion with a maximum amplitude of 1.5° and the pitch angle changes abruptly. When using the‘‘coupled method”, the AOA variation is less than 0.1°, there is no obvious oscillatory motion of the AOA, and the pitch angle changes smoothly. As shown in Fig. 10(h), since the inboard elevons and the drag rudder are ‘‘hard” crossconnected in the ‘‘coupled method”, the inboard elevons will deflect in coordination with the drag rudder, which effectively eliminates the longitudinal disturbance that is induced by thedrag rudder. As the lateral and directional axes are ‘‘soft”cross-connected in the ‘‘coupled method”, the coordinated deflection of the drag rudder effectively reduces the adverse interferences with the lateral response; hence, the ‘‘coupled method” outperforms the ‘‘normal method” in terms of the tracking performance of the roll angle variation rate command and the roll angle changes more smoothly, as depicted in Fig. 10(a) and (e).

Table 6 Lateral-directional flying quality evaluation results.

Table 7 Longitudinal flying quality evaluation results.

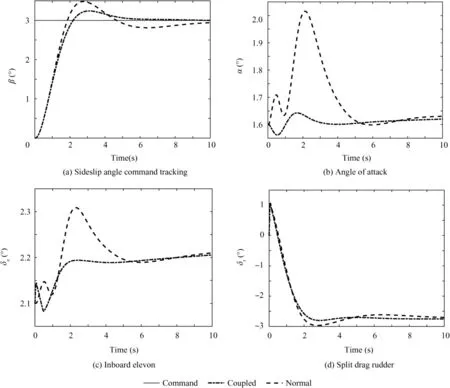
Fig. 9 Numerical simulation of maneuvering command tracking of yaw axis.

In summary, flying wing aircraft can realize improved dynamic decoupling and control decoupling performance by using the ‘‘coupled method”. Moreover, designing the CAS via the three-axis coupled control method is a better choice for satisfying the flight mission requirements.

4.3.Influences of control derivative perturbations of drag rudders on the flight control law

Due to the unique tailless aerodynamic configuration, the dynamic characteristics of flying wing aircraft are significantly different from those of conventional aircraft. Therefore, when selecting the uncertainty parameters for perturbation analysis,we prefer to choose aerodynamic parameters and evaluate the control augmentation and decoupling effects of the three-axis coupled flight control law under variation of aerodynamic characteristics.

In the three-axis coupled control structure, the directional control augmentation parameters and the ‘‘hard” crossconnection decoupling parameters are determined by the yaw and pitch control derivatives of the split drag rudders. The accuracy of these two control derivatives may have significant impacts on the directional dynamic characteristics and the control decoupling performance.Besides,the variation of roll control derivative of the split drag rudders may degrade the lateral-directional decoupling performance. According to the studies in Refs. 6,7,24,37, when compared with other aerodynamic parameter perturbations of flying wing aircraft,the control derivative perturbations of drag rudders have relatively greater influences on the dynamic characteristics of the closed-loop aircraft. Therefore, the following context will put emphasis on analyzing the influences of control derivative perturbations of drag rudders on the three-axis coupled flight control law.

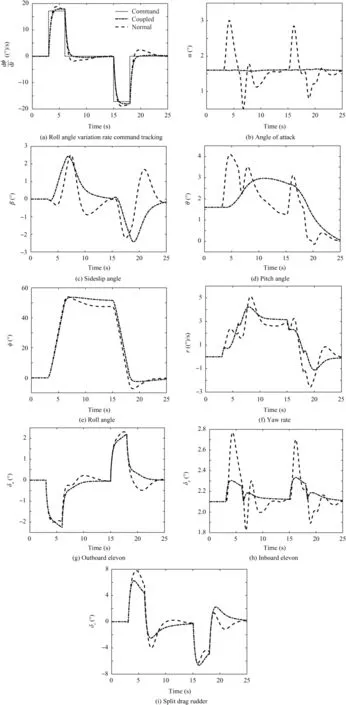
Fig. 10 Coordinated turn maneuver simulation.

To analyze the influences of the yaw and pitch control derivative perturbation of the drag rudder, the yaw maneuver command tracking simulation in Section 4.2.1 is taken as the nominal simulation case, and control derivatives perturbed simulations are performed based on the nominal case using nonlinear simulation model of the aircraft. To analyze the influence of roll control derivative perturbation, the coordinated turn simulation in Section 4.2.2 is taken as nominal case to perform perturbed simulation analysis. Due to the use of nonlinear simulation model in perturbation analysis, the amplitude of roll maneuver command for the coordinated turn simulation has been appropriately adjusted. As for the static aerodynamic parameters of aircraft, by using computational fluid dynamics method or wind tunnel tests, it is capable to obtain high accuracy values, so the deviation range of static aerodynamic parameter is relatively small. According to Ref.37, the parameter deviations of the control derivatives Clδr,Cnδrand Cmδrare determined within range of ±10%. Then perturbed simulation analyses of the three control derivatives are performed separately to determine their influences on the three-axis coupled flight control law.

4.3.1. Perturbation of pitch control derivative Cmδr

The perturbed simulation results for pitch control derivative Cmδrin yaw maneuver command tracking are compared with the nominal simulation result and shown in Fig. 11.

Fig. 11(b) shows that the perturbation of pitch control derivative Cmδrwould slightly affect the dynamic response characteristics of the disturbed AOA. Within 1 s of the simulation time, the disturbed AOA amplitude of perturbed simulations is small when compared with nominal simulation results. Within 1 to 4 s of simulation time, when the control derivative Cmδris increased by 10%, the amplitude of disturbed AOA response is increased by about 0.05° with respect to the nominal value. When the control derivative Cmδris reduced by 10%, the maximum amplitude of AOA response is decreased by about 0.04° compared with the nominal value. After 4 s of simulation time, the AOA responses of the perturbed simulations have nearly converged and are consistent with the nominal simulation result.According to Fig. 11(d), when the control derivative Cmδris perturbed, the ‘‘hard” cross-connection for drag rudder and inboard elevons cannot accurately eliminate the AOA disturbance. But due to the ‘‘soft” cross-connection design for the longitudinal and lateral-directional axes, the inboard elevons can dynamically adjust its deflection according to the AOA disturbance. As shown in Fig. 11(d), when pitch control derivative Cmδris increased by 10%, the deflection of inboard elevons will increase relative to the nominal value to ensure fast convergence of the AOA. When pitch control derivative Cmδris reduced by 10%, the deflection of inboard elevons will decrease relative to the nominal value to avoid generating additional AOA disturbance. Finally, the AOA disturbances induced by the drag rudder are completely eliminated.

Since the pitch control derivative perturbation of drag rudder only affects the longitudinal dynamics, there is very small variation in the lateral-directional state variables in Fig.11s(a)and (c).

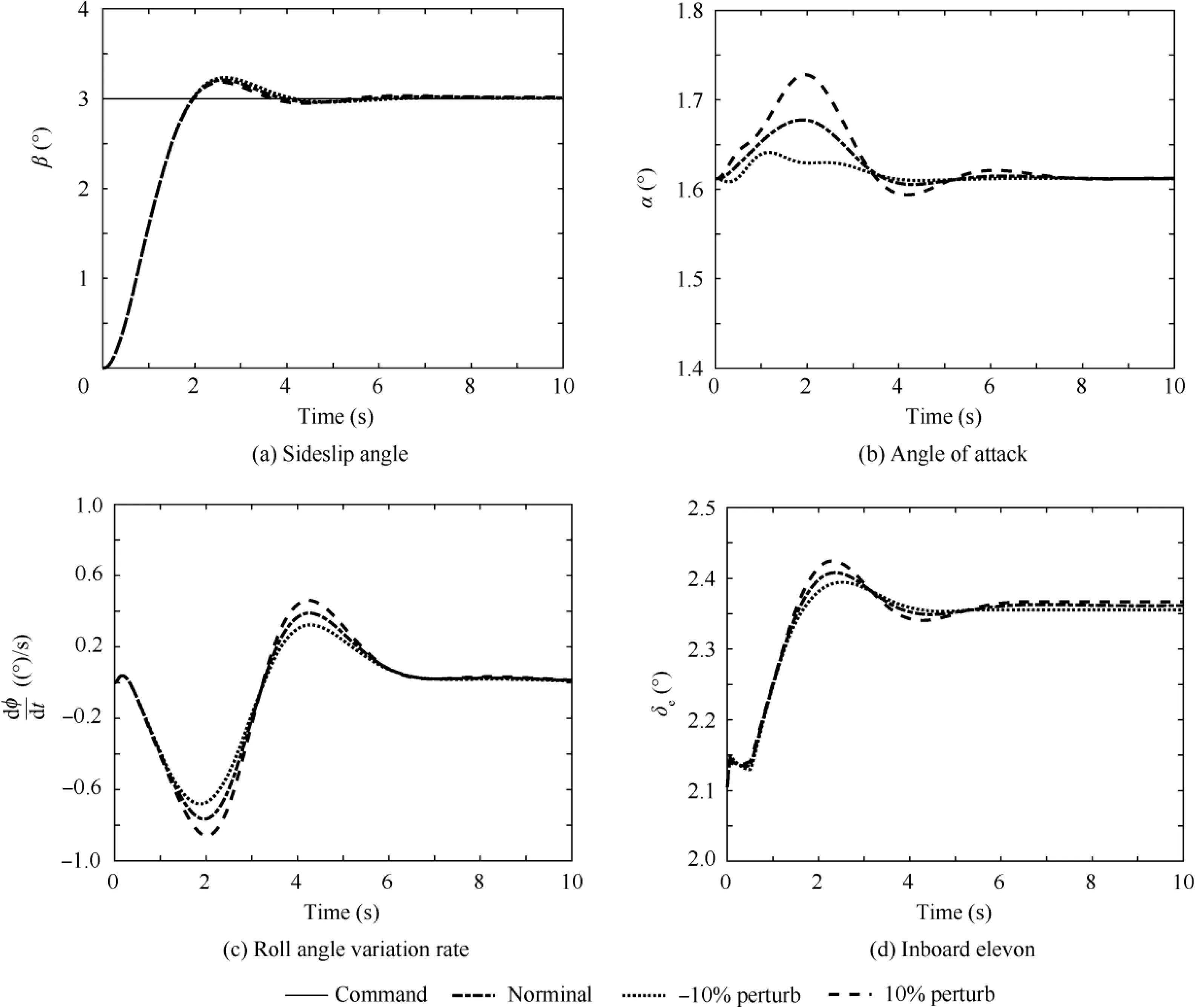
Fig. 11 Perturbed simulation results of pitch control derivative Cmδr.

4.3.2. Perturbation of yaw control derivative Cnδr

The perturbed simulation results for yaw control derivative Cnδrin yaw maneuver command tracking are compared with the nominal simulation result and shown in Fig. 12.

Fig.12(a)and(d)indicate that the perturbation of yaw control derivative Cnδrmainly affects the dynamic response process of sideslip angle. When Cnδris reduced by 10%, the maximum overshoot of the sideslip angle response is increased by approximately 0.5° relative to the nominal result, and the trimmed deflection of split drag rudder is increased from 2.7°of the nominal value to 3° to provide higher control effectiveness.When Cnδris increased by 10%,the overshoot of the sideslip angle response is reduced by about 0.4°with respect to the nominal result, and the trimmed deflection of the split drag rudders is reduced by about 0.3° from the nominal value as a result of increased control effectiveness.In order to quantitatively determine the influence of Cnδrperturbation on the directional flying quality of the flying wing aircraft,LOES matching is performed for the parameter perturbed closed-loop aircraft’s directional axis. The obtained directional LOES models and flying quality parameters are listed in Tables 8 and 9. Table 9 shows that,when Cnδris reduced by 10%,the Dutch roll mode frequency and damping are reduced to 1.14 rad/s and 0.49 respectively. When Cnδris increased by 10%, the Dutch roll mode frequency and damping are reduced to 0.95 rad/s and 0.51. And in both of the two cases, the Dutch roll modes still can meet Level 1 flying quality requirements. Since the feedback yaw rate signal in the directional channel of the closedloop aircraft is calculated by the improved method in Section 2.2, the perturbation of Cnδrwill not significantly change the directional damping characteristics.In both of the two perturbed simulations, the sideslip angle response can quickly reach the steady-state value,and the directional dynamic characteristics are still good.

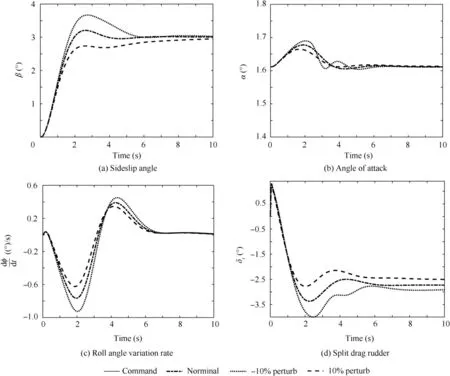
Fig. 12 Perturbed simulation results of yaw control derivative Cnδr.

Table 8 Cnδr perturbed directional LOES model.

Table 9 Cnδr perturbed directional flying quality parameters.

Since the longitudinal-directional axes and lateraldirectional axes adopt ‘‘soft” cross-connection decoupling design, the longitudinal-directional dynamics and the lateraldirectional dynamics can be perfectly decoupled. In Fig. 12(b) and (c), the perturbation of yaw control derivative Cnδrhas little effect on the AOA and the roll angle variation rate responses,and the state responses of the perturbed simulations and the nominal simulation are almost the same.

4.3.3. Perturbation of roll control derivative Clδr

The perturbed simulation results for roll control derivative Clδrin the coordinated turn simulation are compared with the nominal simulation result and shown in Fig. 13.

Fig. 13(a) and (d) show that the roll angle variation rate response and outboard elevon dynamic deflection process of the perturbed simulations are very close to the nominal simulation results. This is because that the lateral-directional axes of closed-loop aircraft are already decoupled by ‘‘soft” cross-connection design, and the absolute value of roll control derivative Clδris much smaller than the value of Clδr, hence the perturbation of Clδrdoes not have significant influence on the lateral dynamics.

The ‘‘soft” cross-connection design for longitudinal and lateral-directional axes can ensure good dynamic decoupling performance,and in Fig.13(b)and(c),the perturbation of roll control derivative Clδrhas almost no influence on AOA and sideslip angle responses.

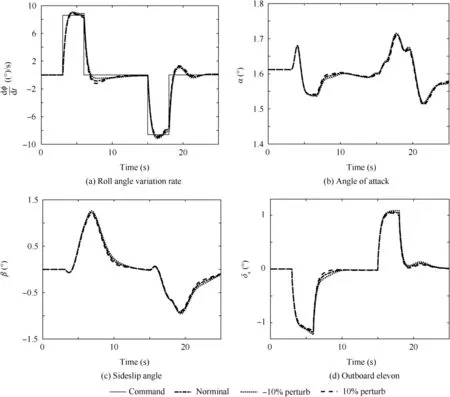
Fig. 13 Perturbed simulation results of roll control derivative Clδr.

5. Conclusions

(1) To improve the poor modal characteristics and to decouple the three-axis control responses from the drag rudder,a three-axis coupled flight control design method is proposed for flying wing aircraft. First, the three-axis coupled control augmentation structure is established.Then, a ‘‘soft” cross-connection design is used for three-axis dynamic decoupling and a ‘‘hard‘‘ crossconnection design is used to realize longitudinal control response decoupling from the drag rudder.Maneuvering turn angular rate estimation and subtraction are used in the directional feedback path to improve the damping characteristics of the Dutch roll mode. The feedback augmentation and maneuver command tracking control parameters are designed via the EA method and the maneuvering command feedforward control parameters are designed via the model following method.

(2) The three-axis coupled flight control design method is evaluated on an example flying wing aircraft. The augmented aircraft can satisfy Level 1 flying quality requirements in all three axes and the Dutch roll mode damping is improved by approximately 30% compared with the‘‘normal method”. Thus, the proposed method effectively improves the handling quality of flying wing aircraft in the yaw axis.

(3) In the yaw maneuver and coordinated turn maneuver simulation examples, when using the ‘‘normal method”,the drag rudder produces long-time oscillatory motions of AOA with maximum amplitudes of 0.5° and 1.5°respectively,while for the‘‘coupled method”,the oscillation of AOA is substantially reduced and the disturbed amplitude is less than 0.1°. The simulation results demonstrate that the three-axis coupled flight control design method has a superior decoupling effect on the drag rudder.

(4) In the control derivatives perturbed simulation examples, the amplitude variation of the disturbed AOA responses caused by the perturbation of pitch control derivative Cmδris within ±0.05°, and the perturbation has ignorable effect on the lateral-directional states.The perturbation of yaw control derivative Cnδraffects the overshoot of the sideslip angle response and Dutch roll modal characteristics. The overshoot amplitude of sideslip angle varies within ±0.5°, while the Dutch roll mode still can meet level 1 flying quality requirements.The perturbation of roll control derivative Clδrhas little influence on the lateral handling quality of the closedloop aircraft, and the longitudinal and directional dynamic responses are not affected. In short, the results of the perturbed simulations indicate that the three-axis coupled control law is robust, and can ensure that the closed-loop aircraft have good control decoupling effect on the drag rudder even though the control derivatives of drag rudder are perturbed.

Acknowledgement

This work was supported by the Fundamental Research Funds for the Central Universities of China(No.:YWF-19-BJ-J-322).