基于FPGA的数字PID控制器研究与设计

何敏龙，肖 峻

(武汉理工大学 机电工程学院，湖北 武汉 430070)

PID控制一直是工业生产中应用最广泛，最成熟的控制手段[1]。据调查，工业控制中有84%的策略采取PID控制，若算上基于PID的各种智能算法，这一数据将超过90%[2]。

在工程实际中具体应用PID控制时，使用微控制器设计数字PID控制器是一种行之有效的方式[3]。笔者使用可编程逻辑门阵列(field programmable gate array,FPGA)设计了数字PID控制器。由于FPGA是并行器件[4]，使用其内部的逻辑资源搭建出PID控制器，可以按照需求与AD采集、数据传输等常用模块连接匹配，彼此之间互相独立，运算效率高，使用方便。

笔者详细阐述了利用FPGA设计数字PID控制器的具体过程。首先通过Matlab进行必要的仿真，得到整个运算的数值范围要求与数值精度要求，以此为依据设计有符号定点加法器和乘法器。然后在Quartus II软件中以Verilog HDL语言编写有限状态机(finite state machine,FSM)来实现PID运算过程，并建立testbench，同样以状态机的方式构建了被控对象的仿真模型。最终在ModelSim仿真软件中进行开环仿真、闭环仿真，保证了PID算法在RTL(real time logistics)级数字逻辑电路上的正确性，具有重要的工程应用价值。

1 PID控制器

1.1 带有限幅的增量式PID控制器

数字PID控制器中通常采用经过限幅的增量式PID算法，其中限幅作用可以避免执行机构因过大的动作而损坏，而将控制量增量的形式表达则易于编程实施[5-6]。其时域表达式如式(1)～式(3)式所示。

du(k)=kp[e(k)-e(k-1)]+kie(k)+kd[e(k)-2e(k-1)+e(k-2)]

(1)

dumax≥du(k)≥dumin

(2)

u(k)=u(k-1)+du(k)

(3)

式中：du(k)为控制量的增量；kp,ki,kd分别为比例系数、积分系数、微分系数；e(k),e(k-1)，e(k-2)分别为当前误差、上一时刻误差和上两时刻误差；dumax为控制量最大限幅值；dumin为控制量最小限幅值；u(k)为控制器输出的控制量。

1.2 软件仿真

考虑被控对象以T=0.001 s进行Z变换，最终得到输出量的时间序列为:

y(k)=0.000 196 7u(k-1)+0.000 195 1u(k-2)+1.951y(k-1)-0.951 2y(k-2)

(4)

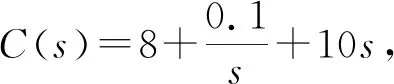
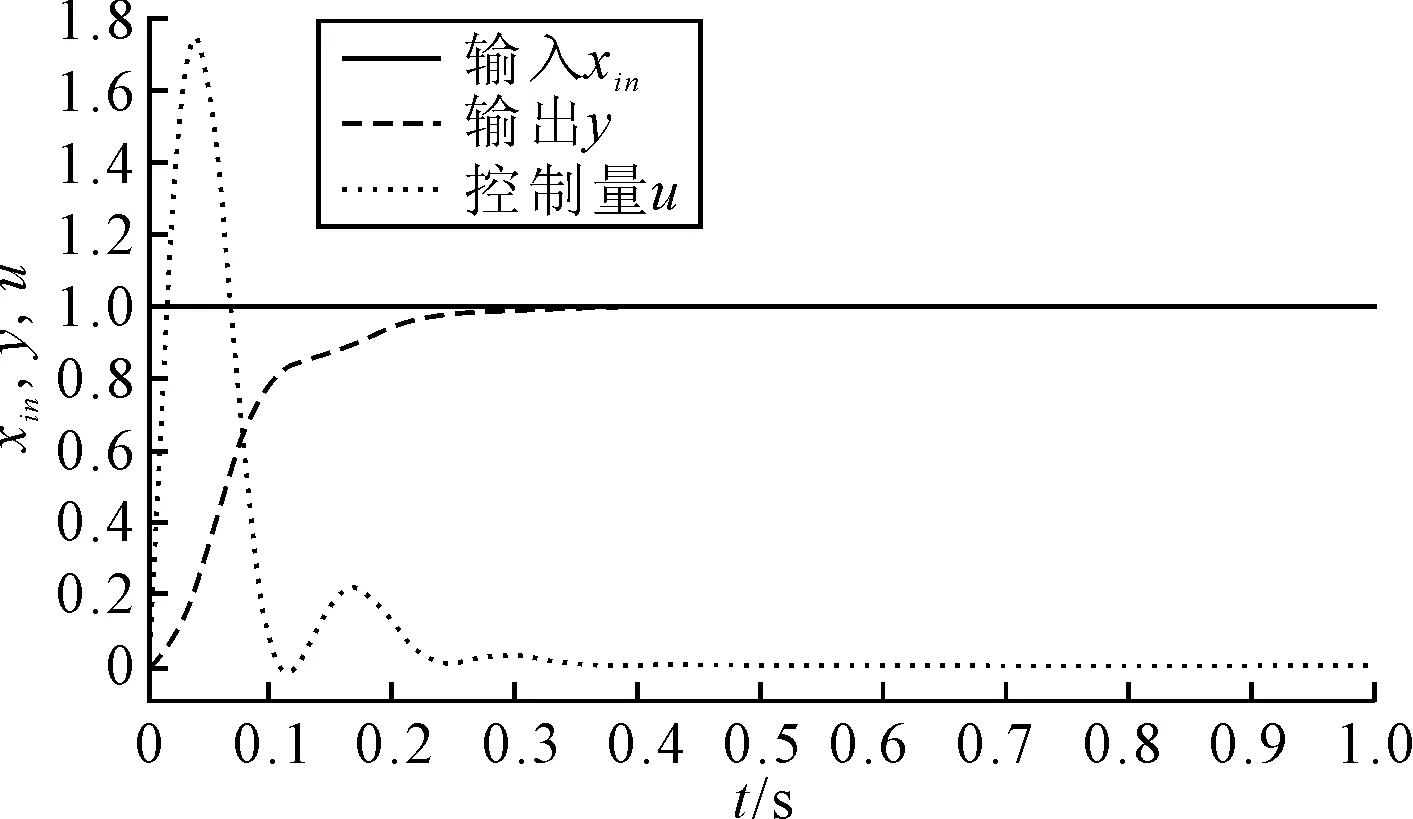
图1 闭环仿真曲线

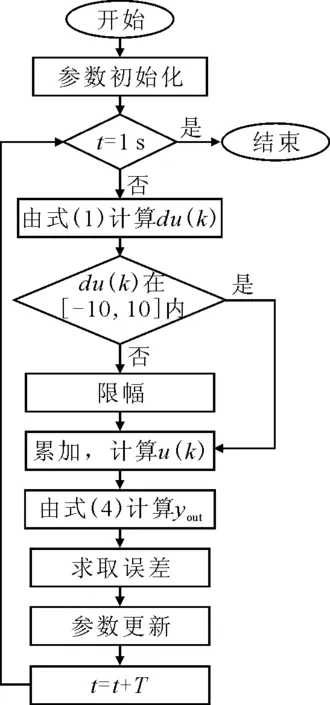
图2 闭环仿真框图

从图1中可知，响应过程无超调，调整时间ts≈0.4 s。同时记录运算过程中的各项数据，绝对值最大的为10，绝对值最小的非负数为0.000 001，这就决定了微控制器中的数据范围要求及数据精度要求。

2 基于FPGA的数字PID控制器

数字PID控制器基于原Altera公司CycloneIV FPGA EP4CE10F17C8芯片设计，主要包括PID控制模块、加法器模块、乘法器模块。其核心是利用单进程的Moore状态机实现式(1)～式(3)的运算。

2.1 加法器模块与乘法器模块

由式(1)～式(3)可知，所有的运算都可以分解为加法和乘法。而FPGA属于数字逻辑器件，正整数之间的加法运算由内部加法器实现，而正整数之间的乘法运算则通过芯片内部已经设计好的嵌入式硬件乘法单元实现[8-9]。然而，本设计过程中涉及到了分数、负数的相关运算，因此需要自行设计加法器、乘法器以满足要求。

根据前文所述，运算过程中绝对值最大的为10，绝对值最小的非负数为0.000 001，因此整数部分至少用4位二进制数表示(24=16)，小数部分至少用20位二进制数表示(2-20=0.000 000 953 7)，才能满足计算的范围及精度要求。最终选取32位的数制，其中最高位表示正负(1表示正，0表示负)，第2位到第12位表示整数，第13位到第32位表示小数，则可以在[-2 048,2 047]内进行运算，运算精度达0.000 001。

按照上述方法设计了32位定点有符号加法器、乘法器，现在通过简单的例子来说明其计算过程。例如：利用FPGA分别计算下面两个式子，在ModelSim中进行仿真，其结果如图3和图4所示。

-60.125+50.25=-9.875

-24.5×(-12.5)=306.25

图3 加法器计算结果界面图

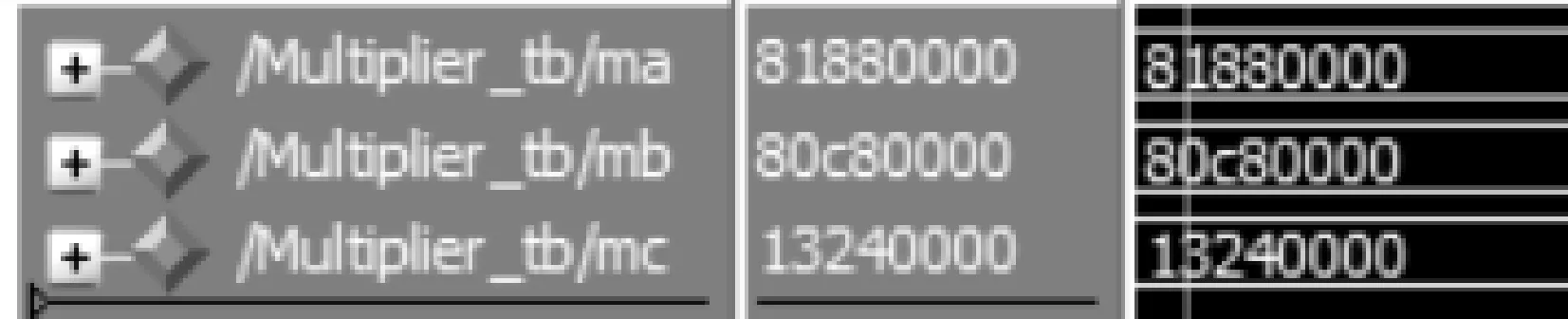
图4 乘法器计算结果界面图

由图3和图4可知，-60.25，50.25，-9.875，-24.5，-12.5,306.25分别用本文所述的32位数据格式表示为32’h83c20000,32’h03240000,32’h809e0000,32’h81880000,32’h80c80000,32’h13240000。故知仿真结果与理论值一致。

2.2 PID控制模块

PID控制模块的核心实现式(1)～式(3)的运算。笔者采取状态机的思路进行设计有3个优点：①状态机结构稳定，不易出错，适合系统中的关键模块设计。②可通过外部驱动定时器，在不影响其余连接模块的情况下改变PID运算的采样周期。③能够增减状态数目，从而实现PID控制的相关变形算法，例如积分分离的PID控制、变速积分PID控制等[10]。实际上笔者所设计的带有限幅的增量式PID控制就是PID控制的一种变形。

所设计的是PID控制模块一个6位的Moore状态机，每个状态都有相应的计算操作，当该状态持续了一定时间就会跳转至下一个状态，而从进入状态st1开始算起，直至回到状态st1所需的时间刚好是1 ms，这就与系统采样周期为1 ms对应起来。

该状态机使用了3个乘法器(Multiplier)和2个加法器(Adder)。进入状态机之前需要进行系统复位，对相关寄存器的值进行初始化；状态机的工作过程如下：

(1)st1，持续100 μs。将e(k)与kp+ki+kd的值赋给Multiplier1，将e(k-1)与kp+2kd的值赋给Multiplier2，将e(k-2)与kd的值赋给Multiplier3，分别计算(kp+ki+kd)e(k)，(kp+2kd)e(k-1)，kde(k-2)。

(2)st2，持续100 μs。将Multiplier1的输出及Multiplier2的输出赋给Adder1，注意Multiplier2的输出需要加上32’h80000000，使加法变为减法，计算(kp+ki+kd)e(k)-(kp+2kd)e(k-1)。

(3)st3，持续200 μs。将Adder1的输出及Multiplier3的输出赋给Adder2，计算du(k)。

(4)st4，持续200 μs。对Adder2的输出进行限幅，即实现10≥du(k)≥-10。

(5)st5，持续200 μs。将st4的输出加到u(k)，实现u(k)=u(k-1)+du(k)。

(6)st6，持续200 μs。内部寄存器移位，并从外界读取最新的误差。

设计完成后，进行开环仿真。令误差恒为1，通过FPGA计算实际值与MATLAB计算的理论值进行对比，结果如表1所示。由表1可知，理论数据和计算数据基本吻合。

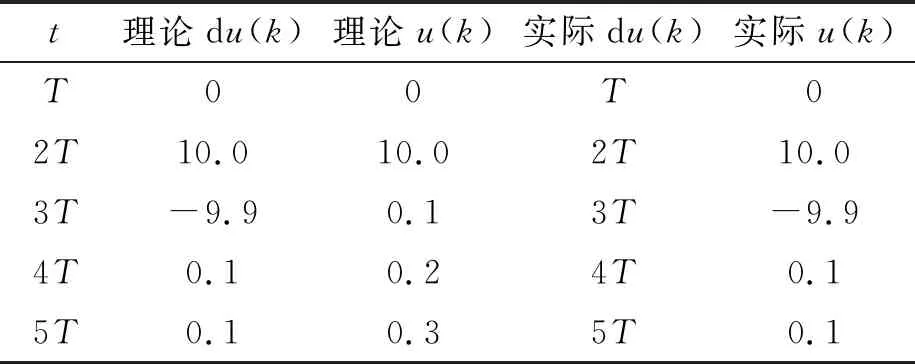
表1 PID控制开环仿真数据对比

3 基于ModelSim的闭环仿真

为了进一步验证PID算法的准确性，采取有限状态机编写了被控对象的模型，并在Quartus II软件中得到仿真文件testbench。首先针对被控对象模块单独进行仿真验证，然后将PID控制模块与被控对象模块联合形成闭环进行了仿真验证。

3.1 被控对象设计

被控对象的时域输出由式(4)决定，据此编写了一个6位的有限状态时实现相应的运算，以1 ms为一个周期进行循环。其中用到了两个乘法器(Multiplier)与两个加法器(Adder)。工作过程如下：

(1)st1，持续100 μs。将1.951与y_1赋给Multiplier1，将-0.951 2与y_2赋给Multiplier2，分别计算1.95y(k-1),-0.951 2y(k-2)。

(2)st2，持续100 μs。将Multiplier1与Multiplier2的结果赋给Adder1，计算1.95y(k-1)-0.951 2y(k-2)；同时将0.000 196 7与u(k-1)赋给Adder1，将0.000 193 5与u(k-2)赋给Adder2，计算0.000 196 7u(k-1)与0.000 193 5u(k-2)。

(3)st3，持续200 μs。将Adder1的结果保存至中间变量Middle，将Multiplier1与Multiplier2的输出赋给Adder1，计算0.000 196 7u(k-1)+0.000 193 5u(k-2)。

(4)st4，持续200 μs。将中间变量Middle与Adder1的输出赋给Adder1，计算y(k)。

(5)st5，持续200 μs。将Adder1的输出赋给yout，计算输出量。

(6)st6，持续200 μs。寄存器移位，并从外界读取最新的控制量u(k)。

设计完成后，进行开环仿真。令控制量恒为1，通过FPGA计算实际值与MATLAB计算的理论值进行对比，结果如表2所示。由表2可知,理论数据和计算数据基本吻合。

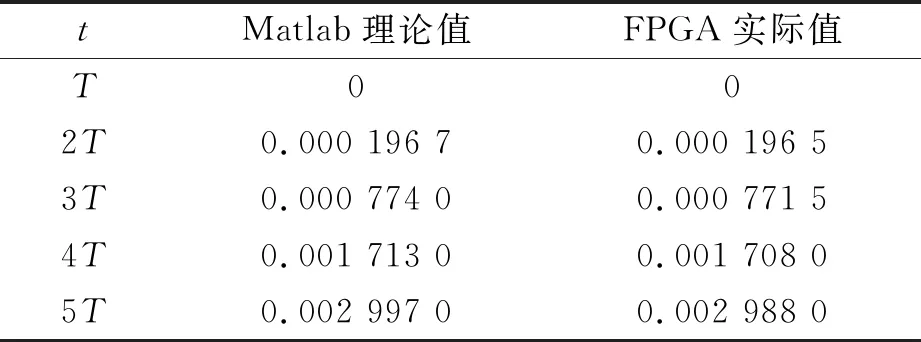
表2 Gs被控对象开环仿真数据对比

3.2 系统闭环仿真

单独设计了数字PID控制器、被控对象的模型之后，在顶层文件中还需要加入误差计算、复位等简单的逻辑，然后将其联合起来进行闭环仿真。如图5所示，是将其联合起来后生成的RTL数字逻辑顶层原理视图。

图5 闭环控制系统RTL视图

进行闭环联合仿真，关键是时序上的匹配。即控制器输出u(k)后，被控模块才会主动读取u(k)；反之，当被控模块输出yout，顶层模块计算出误差之后，才会被控制器模块主动读取。按照本文的设计，相关时序图如图6所示。

在进行闭环仿真之前，还要在tesebench中加入数据转换模块，将du(k)、u(k)、yout分别与0.1相加，使这三个变量都为正值，易于在ModelSim中观测。同时ModelSim的仿真是ps级别，从图1可知，系统的调节时间ts≈0.4 s，对于仿真而言时间过长，考虑等比例缩短状态机时间，将一轮运算周期由1 ms缩短至1 us。进行闭环仿真，如图7所示。

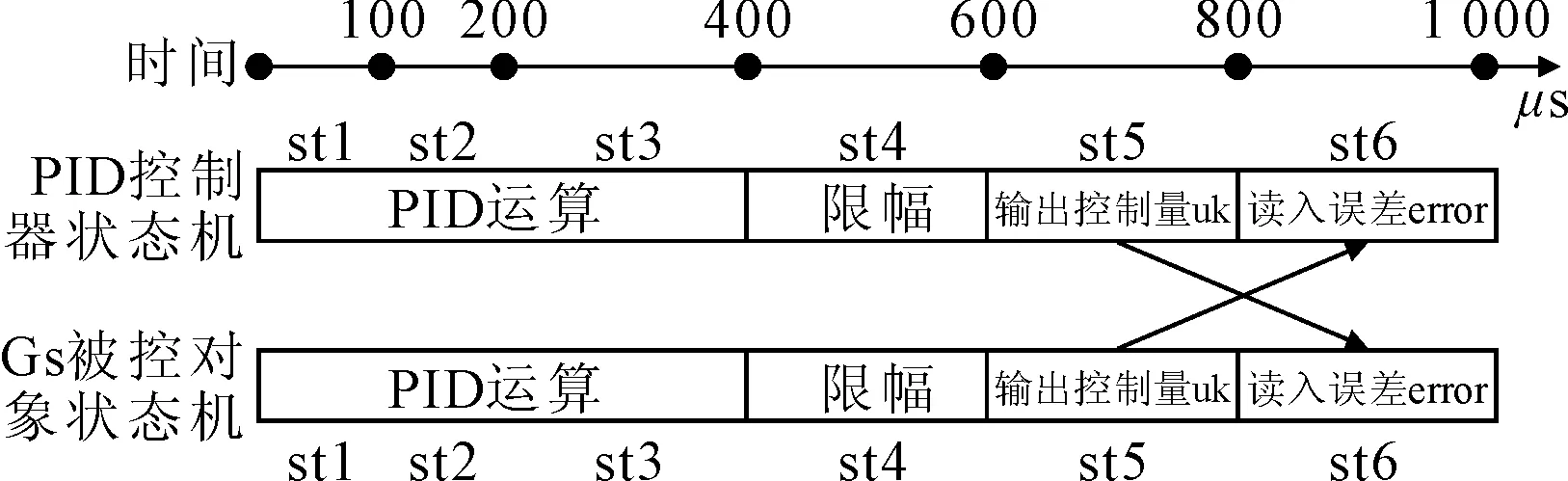
图6 状态机时序图

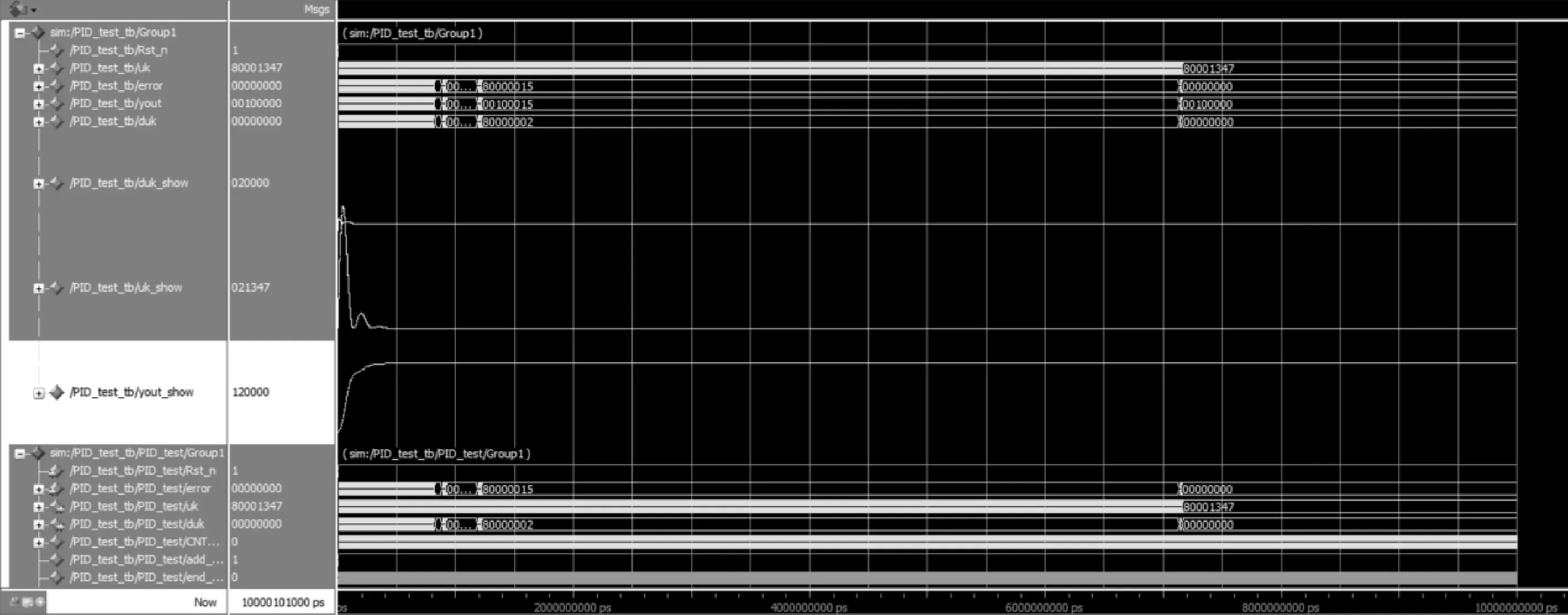
图7 闭环系统仿真

可以发现，图7中的响应曲线yout_show与图1中基本一致。且系统大概在0.42 s进入稳定，在7.2 s误差被完全消除，此时控制量u(k)=-0.004 706。

4 结论

详细阐述了数字PID控制器的设计思路、方法及步骤，完成了各个模块的开环仿真与最终的闭环仿真。主要工作包括数据格式的确定、PID控制状态机的设计、Gs被控对象状态机的设计以及闭环仿真。

在PID状态机中，整体框架不变，改变状态数目，并相应地增加辅助功能，可以设计诸如积分分离的PID、变速积分PID等各种不同的PID控制器。且效果稳定，易于实施，具有良好的工程应用价值。