学会教学反思，做科研型教师

韩旭东

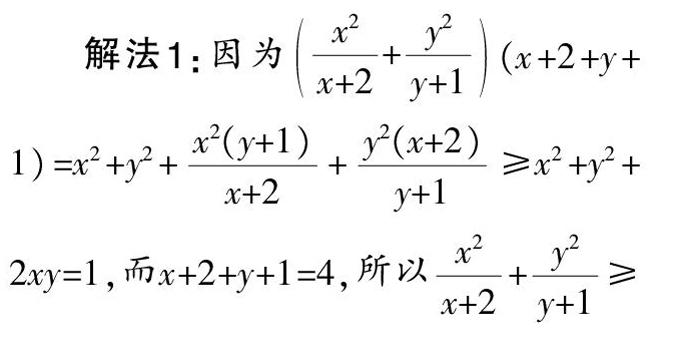
[摘  要] 文章结合教学实践，从教学前、教学中、教学后三个方面谈教学反思，认为教师只有边教边总结，边教边反思，才有希望成为一名科研型的教师.

[关键词] 高中数学;教学反思;科研型;教师

教学反思，即指教师以自己的教学实践为对象，审视并剖析自己的教学过程中的每一个环节，如教学方法、教学效果等等，用教学理论去分析教学实践中不断出现的各种问题，通过问题的研究与解决，以提高教学实效的过程. 熊川武教授认为，反思性教学是教学主体借助行动研究，不断探究与解决自身和教学目的及教学工具等方面的问题，将“学会教学”与“学会学习”结合起来，努力提升教学实践合理性，使自己成为学者型教师的过程[1]. 美国著名心理学家波斯纳认为，不经过反思的经验是狭隘的、肤浅的，没有深度的，教师只有经过不断的反思，才能把经验提升到一定的高度，并对今后的教学实践活动产生深刻的影响. 波斯纳还提出了教师成长的公式：成长=经验+反思[2]. 确是如此，教而不研则浅，研而不教则空，教师只有边教边总结，边教边反思，才有希望成为一名科研型的教师. 那么，教师在教学中该如何反思，反思什么，对此本文提些看法与做法，与同仁们探讨.

在教学前反思

每一次课堂教学是一次有目的的教学活动，目的能否顺利实现，取决于教学设计是否合理，是否符合教学大纲的要求，是否切合学生现有的认识水平，课前是否准备充分，所有这些内容，教学之前必须反思.通过反思不断调整自己的教学计划，积累直接经验，学习间接经验，并在教学中得到充分的发挥，如此，教师的教学水平也必将逐步提高.

如，在学习《平面向量》的概念时，有许多学生把它与实数运算混淆起来.笔者布置了这样一道课外题，批阅时，发现班上有百分之四十左右的学生出现了错误.

例1：设a与b为非零向量，下列命题：①若a与b平行，则a与b向量的方向相同或相反; ②若■=a，■=b，a与b共线，则A，B，C，D四点必在一条直线上;③若a与b共线，则a+b=a+b;④若a与b反向，则a=-■b，其中正确命题的个数是________.

有学生认为①②③④全正确，答案为4;也有学生认为①或④是错的，答案为2或3.

正解：正确的应该是①④，答案为2.共线向量（a与b共线）的充要条件中所存在的常数λ可看作为向量b作伸缩变换成为另一个向量a所作的伸缩量;若a，b为非零向量，则共线的a与b满足a与b同向时a=a■，a与b反向时a= -a■.

出现错解的原因是：学生对向量基础知识理解不正确，把向量运算与实数有关性质运算相混淆. 从学生的错误中，折射出笔者教学中的不足，即教学时没有强调平面向量的几何特征，为此，笔者在接下来的《平面向量的线性运算》的教学中，特别强调平面向量的线性运算的几何意义，引导学生将平面向量的线性运算与实数运算进行对比研究. 于是在教案中设计了如下几个问题.

问题1：对实数来说，a+b的结果是实数，对于向量来说a+b是什么？你能用图形表示吗？

问题2：对实数来说，a-b的结果是实数，对于向量来说a-b是什么？你能用图形表示吗？

问题3：若实数a与b互为相反数，则a+b=0;若a与b互为相反向量，则它们的和还是零吗？若向量a，b，c不共线，则a+b+c=0的几何意义是什么？

问题4：对于实数来说a×b最终的符号如何定？对于数乘向量来说，λa的方向如何确定？

以上四个问题可以说是对准了学生思维的盲点，让学生把平面向量的线性运算与实数的运算严格区分开来. 如果教学前，笔者不加以反思，学生出现的问题有可能重蹈覆辙. 所以说教师的课前反思，十分有必要，它能让教师的教和学生的学都少走弯路.

在教学中反思

任何事物的发展都不是一帆风顺的，数学教学也是如此. 在教学中，必然会出现意想不到的事情发生，这就需要教师当机立断，及时调整教学内容或教学行为. 从课堂实际出发，通过及时的反思与调整，让教学更能激发学生的学习兴趣，让学生主动参与到课堂教学中来. 教学中，反思应主要抓住两个关键点：一是教学难点突破，反思课堂提问和所举的例子是否恰当，是否需要再补充;二是问题情境的设置，数学的学习是由数学问题引发的，我们应该反思所选取问题或例子是否能启发学生的思路，其难度是否处在学生的认知水平之内.

例如，在高三《基本不等式的应用》的复习课上，笔者给出了如下问题.

例2：若正数a，b满足（a-3）（b-2）=6，则ab的最小值为________.

学生经过研究，他们发现了以下两种解法.

解法1：由（a-3）（b-2）=6得ab=2a+3b≥2■，得■≥2■，即ab≥24，所求最小值為24.

解法2：ab=[（a-3）+3][（b-2）+2]

=（a-3）（b-2）+3（b-2）+2（a-3）+6≥6+2■+6=24.

这两种解法都没有采用消元法，而是采用整体代换的思路，是基本不等式应用的“最高境界”，笔者大大表扬了学生，结果发现他们意犹未尽，要求笔者再出一题. 为了满足学生们的需求，笔者又出了一道比刚才一题稍难的题目.

加强练习题：设x，y是正实数，且x+y=1，则■+■的最小值是________.

题目虽然有点难，但经过大约6分钟地苦苦探索，学生还是发现了两种不同解法.

解法1：因为■+■（x+2+y+1）=x2+y2+■+■≥x2+y2+2xy=1，而x+2+y+1=4，所以■+■≥■，即它的最小值为■.

解法2：设x+2=s，y+1=t，则s+t=4， ■+■=■+■=s-4+■+t-2+■=（s+t）+■+■-6=■+■-2. 因为■+■=■■+■（s+t）=■·■+■+5≥■，所以■+■≥■，即它的最小值为■.

由此可见，教案不是上课的“剧本”，教师在教学中对教案应不断做出调整，针对学生上课时的情绪、反应和需求，反思自己原来教学的设计是否合理，是否需要及时改进，只有这样才更有利于学生的学，有利于教学相长，有利于教师的快速成长.

在教学后反思

学之后而知不足，数学教学亦如此.只有善于总结与反思，才能使人进步.上完一节课后，总叫人有所感悟，或成功，或失败.经验要总结，教训更要汲取.上完一堂课后，教师总结的得与失主要包含两个方面，一是来自教师自身，教师上完课后要根据上课的效果，及时总结成功之处、精彩之处和失败之处等等，以便在今后的教学中加以调整;二是来自学生，教师下课后看学生的反应，看学生完成作业的情况，把学生作为一面镜子，反思自己的教学水平. 教师在总结自己的体会与学生的反馈的基础上，找到结合点，然后在师生观点共有的基础上加以创新，发现新的教学契机，为下一节课或者下一轮教学打下良好的基础.此外，教学后反思也是教科研的一种手段，教师可以将其形成论文，以提高自己的专业素养.

在教学中，各知识点的教学要求和例题选择的难度大有讲究，尤其是在基础年级，不可肆意提高教学要求，如幂函数是A级要求，不可当成C级要求来教;不可选择高三的练习来作为例题，否则会加重学生的课业负担，这一点我们必须在教学后加以反思，反思自己的备课与授课是否符合教学大纲，是否符合学生的认知规律.

一次，笔者在高一的函数课上出示了如下一题.

例3：若函数f（x）是定义域为（-∞，0）∪（0，+∞），且它是偶函数，当x>0时，f（x）=2■-1，02，则函数g（x）=4f（x）-1的零点个数为（  ）

A. 4  B. 6  C. 8  D. 10

笔者要求学生合作完成，结果10分钟后，还是没有解决问题. 最后笔者只好自己来讲，由于快要下课了，笔者只能匆匆讲完，草草收场. 听了笔者的讲解，学生还是两眼迷茫. 此时，笔者顿觉这节课自己上得好失败，需要好好反思. 首先，笔者反思了这道题的难度. 这道题把分段函數、函数的性质、函数与方程等知识点综合在了一起，是一道高三总复习题，难度较大，不适宜高一学生.其次，笔者反思了教法. 如果要让学生完成这道题，就应做好必要的铺垫，如：问题1：与分段函数有关的零点问题一般采用哪种方法？（数形结合，即图像法）问题2：f（x）=■f（x-2）是一种怎样的图像变换. 如果笔者给出以上两个铺垫，那么学生一定能顺利完成. 反思结果：备课必须从学生的实际出发，必须注重每一个细节，只有这样的课堂才是有效的课堂.

？摇总而言之，作为教师，要活到老，学到老，反思到老. 把反思当成一种习惯，其实反思也是一种学习，是一种自我学习，这种“学习”可以加速教师成长，使课堂教学不断优化，使教学水平、教学能力和教学效果不断提高[3]. 实践证明：教师只有不断反思自己的教学行为，才能从反思中感悟，从反思中积累，长期坚持，必有所得，从而把自己从“教书匠”渐渐地演变成讲究科学教育，具有科研能力和钻研精神的受学生喜爱的“大先生”.

参考文献：

[1]  熊川武. 说反思性教学的理论与实践[J]. 上海教育科研，2002（06）.

[2]  张祥锦. 课例研究：教师专业成长的有效路径[J].江苏教育，2018（70）.

[3]  毛齐明. 教师有效学习的机制研究[D]. 华东师范大学，2010.