数学问题情境创设之我见
刘宏飞
[摘 要] 部分教师教学时一味倾向于接受与掌握,缺乏引导学生发现与探索,导致学生的思维长期处于被动状态. 教学实践说明,通过有意识地创设生活问题情境、趣味问题情境、矛盾问题情境、开放问题情境等,可以将学生的思维引向深入,为学生的创新发展打开一扇窗.
[关键词] 数学教学;问题情境;创设;深度学习
教育心理学认为学生的学习方式分为接受式学习和发现式学习这两种,而这两种学习方式应当是相辅相成、紧密融合的. 然而传统教学中,不少教师更倾向于强调接受与掌握,完全忽视了发现与探究,从而导致了学生学习积极性较低,学习兴趣缺失,学习效果自然较低. 当下,研修学习如火如荼地推进着,数学教师需有意识地创设生动形象的问题情境,关注学生的发现、探究和研究等认知活动,使学生产生学习的动力,发展学生的数学核心素养[1]. 下面笔者结合多个案例,谈谈如何从问题情境的创设开始,将学生的思维引向深入,为学生的创新发展打开一扇窗.
生活問题情境
新课程改革的推进下,对数学新教材提出了更高的要求,希望更贴近生活,使学生在生活中学数学,这样生活化的课堂营造的是一种“生活场”,让学生体验到数学的丰富多彩与生动活泼,从而学习到“活”的数学,有意义的数学. 因此,我们在课堂教学中需善于选取学生身边感兴趣的事物或生活实例,唤起学生思考生活中的数学,让数学课堂更具生活味.
案例1:以“导数”的教学片段为例
问题呈现:某公司打算在大门处一块边长为200 m的正方形空地上建一个花圃,并在四个顶点处各建一座凉亭供员工小憩,这样一来,则需构造一个使得任意两个凉亭都可通行的道路网. 现请你为设计师小王出谋划策设计合理道理网方案,使得其总长度最短. (取■=1.414,■=1.732)
这样的情境创设,一下子吸引了学生的注意,使得他们积极主动投入到探究活动之中,并生成了各种各样的解题策略.
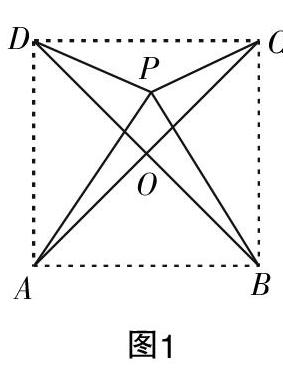
生1:如图1,设四个凉亭分别为A,B,C,D,连接两条对角线即可形成通道,并求出总长度为400■=565.6 m.
师:生1的思路设计是正确的,但是否可以使通道最短呢?
生2:分析图1,据平面几何知识可得:在正方形ABCD所在平面上任意取一点P,分别连接PA,PB,PC,PD即为所需修建的道路网. 当点P与O重合时,该道路网必定最短. (其余学生纷纷点头赞同)
师:这种思路真的是最捷径的吗?
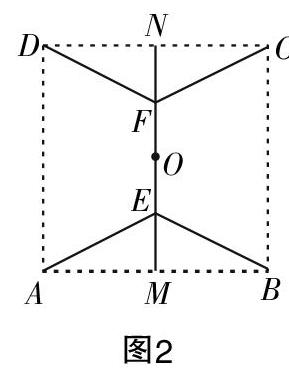
生3:我的想法与他不同. 我觉得若要减少总长度,就需增加通道的公共部分,要知道正方形是轴对称和中心对称图形,那么如图2,过中心O设计一段公共道路EF,使得EF⊥AB,设OE=OF=x(0≤x≤100),则道路总长为y=2x+4■;再运用导数求函数最小值即可求出道路网总长的最小值为546.4 m.
师:多么巧妙的思路,多么创意的想法,真是妙极了!
……
以上案例中,生3的思路令人惊叹!事实上,他的巧妙思维源于他勇于探索和不断创新的精神,通过具有生活问题情境的创设,不但可以激起学生的探究兴趣,还可以使探究活动变得丰富多彩,利于创新意识和研究能力的培养.
趣味问题情境
心理学研究显示,学生学习情绪状态越好,就会形成较好的学习效果. 因此,在课堂教学中,教师可创设生动有趣的问题情境,以此来调动课堂气氛,激发学生的学习情趣,继而形成问题的学习兴趣与强烈的思维火花.
案例2:以“等比数列”的概念引入为例
问题呈现:阿基里斯与乌龟约定举行一场赛跑比赛,乌龟在阿基里斯的前方1千米处,而阿基里斯的速度是乌龟的10倍,当他追到1千米处,乌龟前进了■千米;当他追到■千米处,乌龟前进了■千米;当他追到■千米处,乌龟前进了■千米……
(1)试着分别写一写同时间段内阿基里斯与乌龟各自所前进的路程;
(2)你觉得阿基里斯可以追上乌龟吗?
这一问题一出,激起了学生探求新知的欲望. 通过这一问题推进教学,自然引出等比数列的定义,让学生投入主动学习的良好状态.
矛盾问题情境
学生都是独具个性的个体,在知识、经验、能力及思维方式上或多或少存在着差异性,对同一事物或问题会形成不同的思考或见解. 教学中教师有意识地针对课堂内容设计,将矛盾问题情境运用到教学活动中去,挑起“矛盾”,引发学生的争辩,进而产生较强的探索动机,并通过化解矛盾来培养学生的发散思维,为综合思维的养成奠定良好的基础.
案例3:已知双曲线■-■=1上一点P到右焦点的距离为5,则以下结论中正确的是( )
A. 点P到左焦点的距离为8
B. 点P到左焦点的距离为15?摇
C. 点P到左焦点的距离无法确定
D. 这样的点P不存在
这是一道数学模拟试题,难度不算太大,但是做错的学生并不少,究其根本在于学生容易忽视双曲线定义的一些限制条件. 笔者首先引导学生独立思考并解答,同时在来回巡视中找寻一些错误解法,以此作为可生成性资源进行板演:
错解1:设双曲线的左、右焦点分别为E,F,据双曲线定义,可得PF1-PF2= ±10. 因为PF1=5,所以PF2=PF1+10=15,故本题选B.
错解2:设P(x■,y■)为双曲线左支上的一点,则有PF2=ex■-a,据条件得a=5,PF2=5,于是ex■=10,PF1=ex■+a=15,故本题选B.
同一个问题通过两种不同的解法得出了一致的答案,那么该结论就应该是正确的了. 但真的正确吗?此时教师可启发学生进行反思辨析,学生经过讨论、争辩后找寻到了出错的原因:若PF2=5,PF1=15,则有PF1+PF2=20,而F1F2=2c=26,则有PF1+PF2 通过以上案例的辨析,让学生不断比较、不断探究、不断反思,从“陷阱”中跳出来,增强抵御“陷阱”的能力,并在认知冲突与平衡的反复循环中强化自身的认识,在讨论与辨析的反复推进中获得学习主动权,从而使其对问题的认知从感性上升到理性,从现象上升到本质,积累数学发现的经验,培养创新意识和能力. 开放性问题情境 学生思维的提升程度与有价值的问题引导是密不可分的,因此,教师需有目的地开放课堂,从教学内容出发,基于具体学情创造教学因子,通过开放性问题情境为学生的创新提供展示思维的平台,从而将教学的过程营造成发现创造的过程,充分调动学生学习数学的能动性,推动思维的涟漪[2]. 案例4:直线y=3x+m与抛物线y=x2相交于点A和B,________,试求出直线AB的方程. (请在横线上补充一个恰当的条件) 此问题作为条件开放的问题,引起了学生的兴趣,另一方面提升了学生分析和解决问题的能力. 学生有了思考的欲望,有了展示成果的热情,补充了多种多样的条件,如:①AB=■;②OA⊥OB;③y轴平分线段AB;④段AB的中点到y轴的距离最短,等等. 以上开放性问题情境所涉知识宽度是显而易见的,其中不乏韦达定理、弦长公式、中点坐标公式等重要基本知识,还运用了数形结合等重要思想方法,可以说学生真正意义上进入自主学习的状态,深度思考在课堂上真正发展,学生的能力也自然形成了. 总之,一个良好的问题情境可以引发学生的思考、质疑、争辩和讨论,在营造良好的学习氛围的同时促进学生积极思考和主动探究,让他们更积极主动地参与学习,为他们供给创新“养料”,让他们迈入创新之路. 为了激发学生火热的思考,良好的问题情境应贯穿于整个教学的始终. 参考文献: [1] 汪亚亚. 新课程背景下高中数学情境创设对策研究[J].读写算,2018(06). [2] 陈红军. 探究式教学在高中数学课堂教学中的运用[J]. 教师博览(科研版),2015(03).

