三道赛题的有趣推广
2020-10-19 09:23武增明
数理化解题研究 2020年28期
武增明
(云南省玉溪第一中学 653100)
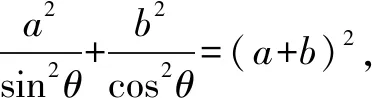
此题可以推得以下有趣的推广命题.
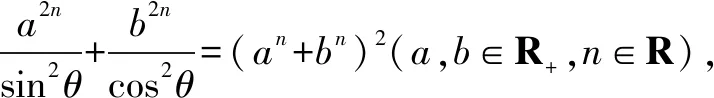
证明由柯西不等式,得
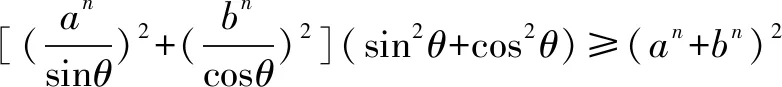
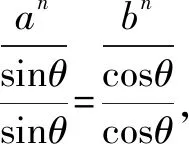

此题可以推得以下有趣的推广命题.
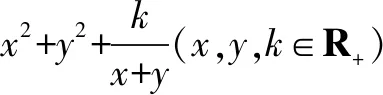
证明由二元及三元均值不等式,得
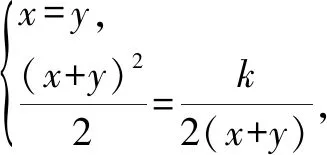
说明由推广命题的证明可以看出,原赛题中的条件x3+y3=2是多余的.
赛题3(2016年全国高中数学联合竞赛湖北省预赛高一赛题)如果存在实数a,使得关于x的不等式acosx+bcos2x>1无实数解,那么实数b的最大值为____.
此题可以推得以下有趣的推广命题.
命题设c为正常数,如果存在实数a,使得关于x的不等式acosx+bcos2x>c无实数解,那么实数b的最大值为c.
证明因为关于x的不等式acosx+bcos2x>c无实数解,所以关于x的不等式acosx+bcos2x≤c的解集为R.
所以取x=0,得a+b≤c;取x=π,得b-a≤c.
两式相加,即得b≤c.
当b=c时,取a=0,此时原不等式为cos2x>1,显然无解.所以实数b的最大值为c.
猜你喜欢
中等数学(2022年7期)2022-10-24
中等数学(2022年5期)2022-08-29
中等数学(2022年1期)2022-06-05
中等数学(2022年2期)2022-06-05
中等数学(2021年7期)2021-11-22
语数外学习·高中版中旬(2020年2期)2020-09-10
中等数学(2020年3期)2020-08-24
河北理科教学研究(2020年1期)2020-07-24
中等数学(2018年4期)2018-08-01
高中生学习·高三版(2017年6期)2017-06-12

