2020年高考江苏卷第12题的七种解法

蔡海涛 卢 妮

(福建省莆田第二中学 351131)

题目(2020年高考江苏卷12)已知5x2y2+y4=1(x,y∈R)，则x2+y2的最小值是____．

点评利用消元转换消去x，把x2+y2化为只含有y一个变量的式子，再利用基本不等式求得求值.多元变量求最值问题利用消元转化是常规套路，利用基本不等式要注意“一定、二正、三等号”.

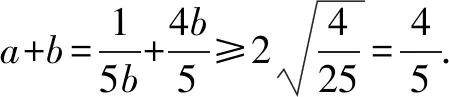
解法3 同解法2把问题转化为求a+b的最小值.

点评解法2基本思路同解法1，均是先利用消元转化再利用基本不等式求得最值，区别之处是发现已知和要求的式子次数较高，先利用换元进行降幂，使得运算简化.解法3关键是注意到5ab+b2为定值，故进行配凑再利用基本不等式得到一个关于a+b的不等关系，从而求得a+b的范围.

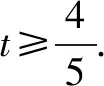
点评首先把a+b看作一个整体t，再得到关于b的一元二次方程，利用判别式求得t的范围.

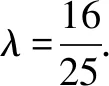
点评考虑将式子a2+(2-5λ)ab+(1-λ)b2配成一个完全平方式，故令Δ=(2-5λ)2-4(1-λ)=0，求得λ的值，进而得到(a+b)2的不等关系，求得范围.

解法6 同解法2，5ab+b2=1，则(5a+1)b=1(a,b≥0).

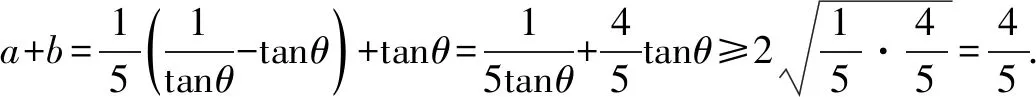
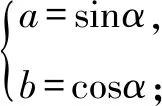
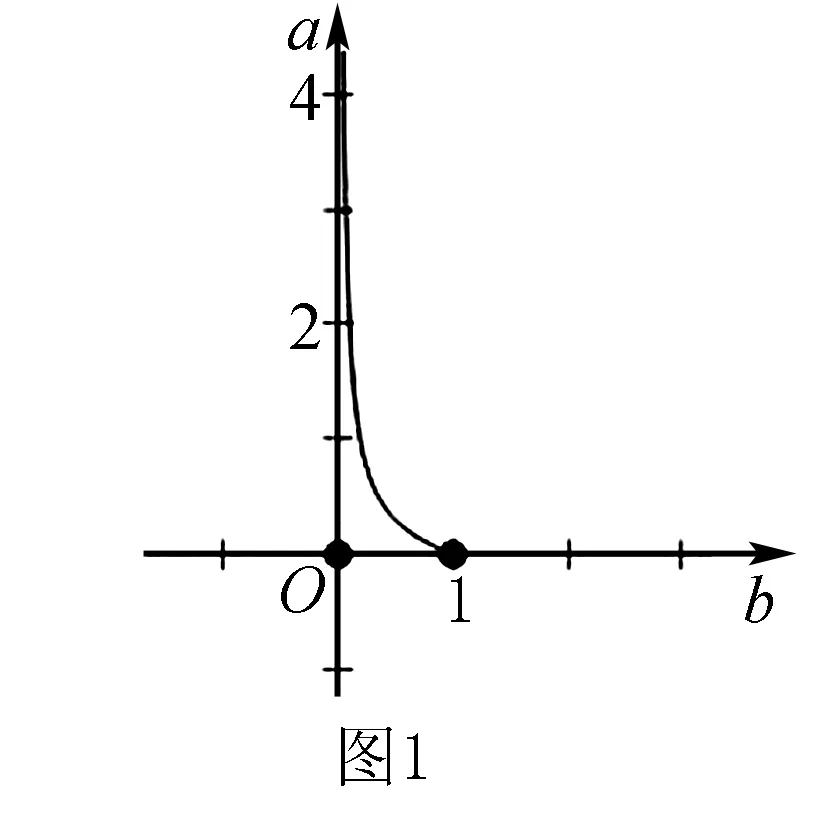
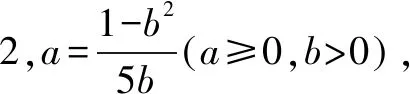
点评双变量问题常常可以通过确定主元,看成一个函数关系来进行处理.

多元变量最值问题在近年各地高考中频频出现，其特殊的解析式结构决定其具有知识覆盖面广、综合性强、解题方法灵活多样的特点.通过以上高考题的多解分析,可总结方法一般是从数和形两个角度着手进行研究.从数的角度出发，常常是利用函数方程思想，进行消元转化，结合换元简化，再利用基本不等式求得范围；从形的角度出发,常常是发现多元变量之间的关系，具有怎样的几何意义，再利用几何特征判断取得最值的位置，最后求得范围.