等径变距螺旋结构设计与仿真

李飞翔宗向东 李永祥 付俊辉

(1. 河南工业大学机电工程学院，河南 郑州 450001；2. 登封市轩程控设备有限公司，河南 登封 452470)

螺旋给料装置常常被用于粉体物料的定量给料中，为解决小麦粉螺旋进料段下料不均匀问题，国内外学者在螺旋结构设计上进行了大量研究。郝友莉等[1]针对粉体夹气输送效率低的问题，基于变距螺旋结构设计方法设计了四段式变螺距螺杆，提高了系统的包装效率。Orefice等[2]基于离散单元法对螺旋输送机中物料颗粒的体积流量与螺旋轴尺寸及物料颗粒与壁面摩擦系数间的关系进行了研究，确定了螺旋输送机的最佳结构参数，最大限度地提高了输送效率。Pezo等[3]基于离散元法对5种不同长度的改进型水平单螺距螺旋输送机进行了研究，针对输送中的辅助混合进行了优化设计，并以透明外筒进行试验分析，建立了预测混合质量的数学模型。

常规的等径等距螺旋装置，其粉体在料斗内会出现死区现象[4-5]。赵冬梅等[6]针对螺旋输送机出料口方向物料不均的问题，采用变距设计并提出了一种指数型拟合法，通过离散单元法对变距螺旋结构性能指标进行了分析，并对输送性能较佳的指数型方法设计了变距参数界面。Bates等[7]针对螺旋进料段下料不均的问题，对不同螺杆形式物料下料的流动特性进行了分析，概述了物料在料斗中的运动规律并对其进行了理论研究，为不同结构螺杆的选取设计提供了理论依据。Fernandez等[8]针对螺杆设计大多基于分析模型而无法实现料斗内物料流型预测的问题，采用离散元法(DEM)对水平螺旋给料机系统中的颗粒输送进行了预测，研究了不同螺杆对料斗颗粒流量、下料均匀度、螺杆磨损及壁摩擦变化的影响。

试验拟提出一种新的等径变距螺旋结构设计法以提高小麦粉螺旋给料的精度，对螺距与螺旋轴向距离间关系进行假设分析，根据所得螺距设计方程及设计要求，采用Solidworks软件建立三维模型并以小麦粉物料对其进行离散元仿真，观察螺旋进料段下料量及料口流量的稳定性，并与等距螺旋结构进行对比分析，旨在为解决小麦粉螺旋进料段下料不均匀的问题。

1 变螺距设计

1.1 基本理论

等径变距螺旋结构工作时，其物料在料筒内的运动状态非常复杂，为分析料筒内物料运动变化规律，在建立变距螺旋轴参数化模型前需进行合理假设[9]：

(1) 不考虑物料压实现象。

(2) 螺旋物料的轴向速度同螺旋叶片的轴向速度相同。

将螺旋轴向定为x坐标轴方向(见图1),x轴上一点相当于垂直于螺旋轴的一个截面，其原点定于螺旋始端，螺旋叶片转角α为x的函数α=f(x)。

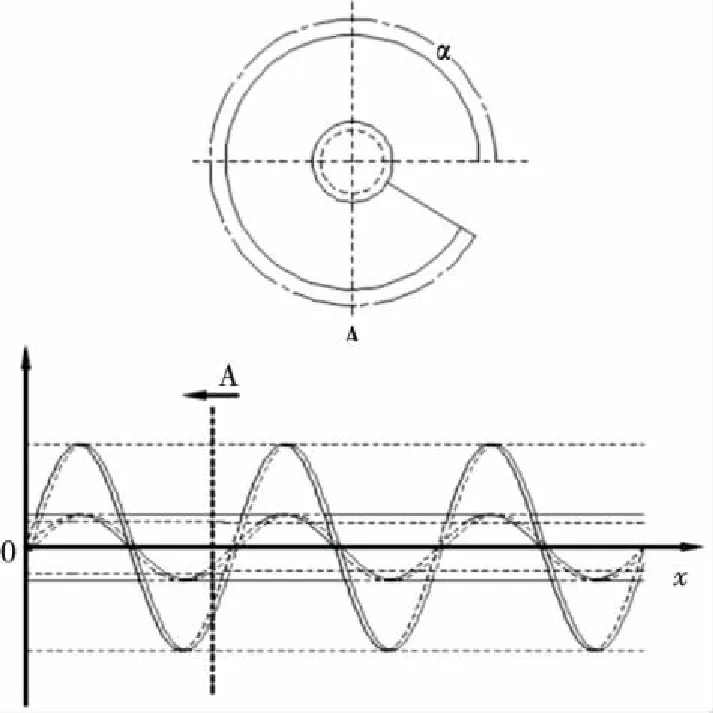
图1 x轴的螺旋叶片转角示意图Figure 1 x schematic diagram of the rotation angle of the spiral blade

设v为物料轴向速度，则在x截面任一点P的物料轴向速度表示为vp，根据流量定义有：

Q=∬Dvdσ，

(1)

式中：

Q——螺旋产量，t/h；

v——物料轴向速度，m/s；

D——x截面的整个区域；

σ——面积元素。

对于不同的x截面，物料流量Q不同。流量差值△Q=Qx+△x-Qx，即在x轴向范围内料仓中物料进入螺旋的料流。根据上述所提要求，在整个x轴区间内，不论dx为何值，单位长度的物料需均匀一致。用数学方程表达为：

(2)

其中A为常数，将其表达成导数形式：

(3)

解得：

Q=Ax+Q0，

(4)

式中：

Q0——螺旋始段的物料流量，t/h。

如果螺旋的螺距变化不太大，在x截面的螺旋叶片能达到的整个圆形区域上，物料的轴向速度相同，即

(5)

式中：

w——角速度，r/s；

S——螺距，m。

则物料流量为

(6)

式中：

R——螺旋叶片外径，m；

r——螺旋轴半径，m。

由式(4)、(6)可知：

(7)

当螺旋为等直径变螺距时，式(7)可改写为：

(8)

S=Bx+S0，

(9)

(10)

(11)

因此，对于等径变距螺旋结构，为保证下料的均匀稳定，螺距随x线性增加。

1.2 螺距设计

由螺距随x的线性变化进行分析，设螺距与x的线性方程为：

S=kx+b。

(12)

由图2可知：

x=x1=S1时，S=S1；

x=x2=S1+S2时，S=S2；

x=x3=S1+S2+S3时,S=S3；

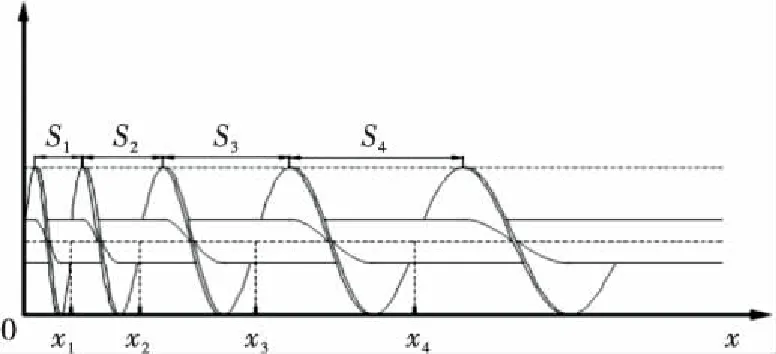
图2 等径变距螺旋图Figure 2 Equal diameter variable pitch spiral diagram

…

x=xn=S1+S2+S3+…+Sn时,S=Sn。

线性方程斜率k为：

(13)

根据斜率及设定坐标点可知，

(14)

解得系数b为：

(15)

则变距螺旋结构螺距与轴向x的线性方程为：

(16)

式(16)为理想假设条件下，考虑粉体物料进料段下料均匀性所推导的螺距随轴向x变化的函数，可对螺旋结构优化设计的参数进行分析验证。根据斜率可知：

(17)

各螺距与首圈螺距值之间的关系为：

(18)

由式(18)可知首圈螺距值、末端螺距值、斜率和进料段圈数间的关系，首圈螺距及末端螺距的选取可根据设计要求确定，进料段圈数的确定与进料段的总长度L密切相关。由进料段各圈螺距的总和为L可知：

(19)

斜率k为：

(20)

若将Sn代入式(20)可得：

(21)

实际上，螺旋进料段的设计需根据设计要求、机构尺寸等约束条件来确定螺距值，由式(21)即可根据进料段的长度、首圈螺距值和设计要求得斜率，也可根据斜率和首圈螺距值求得段数。然而，假设理想条件下，仅当斜率k趋于0时，等式成立，因此，采用此方法进行设计需先确定首圈螺距值及末端螺距值，首圈螺距值一般取S1≥0.25D。为保证螺旋内物料输送均匀，进料段的末端螺距值一般取Sn=0.8D～1.0D。根据首圈及末圈螺距值计算出斜率后，从首圈螺距值开始向末端进行推导计算其他各螺距值。

2 设计实例与仿真分析

2.1 设计实例

已知试验物料为小麦粉，容重r=0.52 t/m3，综合特性系数A=75，填充率φ=0.4，螺旋给料装置生产率Q=0.8 t/h，螺旋总长度L=800 mm，进料段长度l=300 mm，螺旋转速n=80 r/min，螺旋轴径d=30 mm，输送段螺距Sn=80 mm，进料段首圈螺距值S1=25 mm。

将已知数据代入式(20)可得斜率k=0.2，根据式(17)从首圈螺距值开始向末端进行推导计算其他各螺距值：

S1=25 mm;S2=32 mm;S3=40 mm;S4=50 mm;S5=65 mm;S6=77 mm。

2.2 仿真分析

2.2.1 仿真参数 采用前期小麦粉标定结果进行仿真试验[10]，小麦粉仿真参数如表1所示。

表1 小麦粉放大颗粒离散元仿真参数表

2.2.2 仿真过程 采用Solidworks软件建立螺旋结构三维模型，然后将模型导入至离散元软件进行模拟分析。结合相关文献[11-12]，颗粒生成方式为 Dynamic，首先在螺旋进料段料斗部分设立颗粒工厂，设定较大的颗粒生成速度，使粉体物料颗粒能快速充满料斗，然后停止生产颗粒，待物料处于静止时，暂停仿真，对仿真环境进行重新设定，使料斗中的物料最顶端处于水平状态，距料筒中心线距离为300 mm，为后续进料段下料均匀性的对比分析作铺垫。然后开始设定螺旋转速，根据要求设定为100 r/min，为便于后处理观察，步长设定为0.05 s，仿真时间设为10 s。

2.2.3 常规等距螺旋下料均匀性分析 等径等距螺旋是最常规的螺旋结构，参照文献[13]的方法对螺旋进料段的下料均匀性进行分析。采用后处理中的Geometry Bin工具建立色带区域，在物料输送前分别对其进行上色处理，如图3所示，依次为红紫黄绿青，料筒中的色带上为白色。仿真时间设定为10 s，分别取5，10 s两个时间节点处物料的运动状态图进行分析对比。

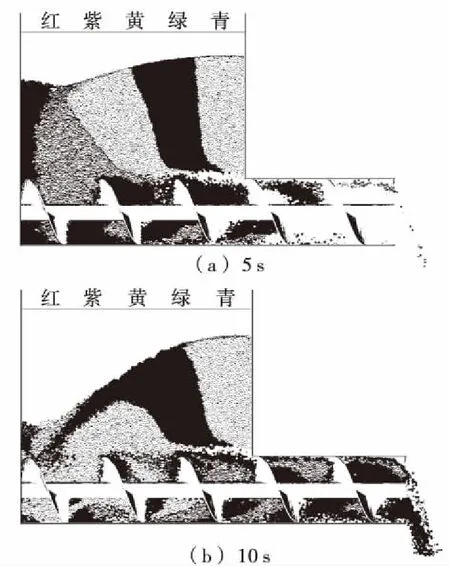
图3 等螺距仿真图Figure 3 Equal pitch simulation diagram

由图3可知，当仿真时间为5 s时，料斗中的青色色带和绿色色带基本处于垂直状态，黄色色带有向第一圈螺距倾斜的趋势，料斗中形成轻微的漏斗状。此时，螺旋料筒中基本没有黄绿青色带的物料颗粒，螺旋的进料段主要有红色和紫色的颗粒，料斗中的红色色带明显变细，并有轻微的死区现象，死区部分主要为黄绿青色带区域。当仿真时间为10 s时，料斗中红紫色带基本已消失，物料形成明显的漏斗状，白色物料已完全被输送，黄色物料大部分进入进料段，此时可明显观察到等距螺旋结构的死区现象，整个进料段中，料斗中物料均逐渐从第一圈螺距开始输送，其他螺距段料斗中的物料形成明显的死区现象。

2.2.4 等径等距螺旋速度分析 同样采用两个时间节点分析等距螺旋速度，采用三色模式，暗红、红、蓝速度大小依次递减，其速度分布如图4所示。由图4可知，当仿真时间为5 s时，物料处于轻微的死区现象，料斗中物料流动较小，速度分布较为均匀；料筒中，在螺旋体附近及料筒内壁处的物料颗粒显红色，速度相对较大。当仿真时间为10 s时，物料处于明显的死区现象，料斗中物料出现明显的漏斗状，沿着物料的滑移面，物料表面颗粒处于向第一圈螺距移动的趋势，速度相对较大。

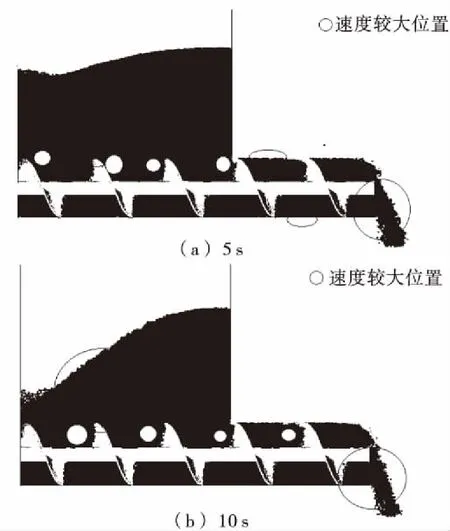
图4 等距螺旋速度分布图Figure 4 Isometric spiral velocity distribution

2.2.5 等距螺旋流量分析 采用给料稳定段6～8 s对螺旋流量进行分析。采用后处理中的流量传感器，设定位置为料筒末端口，对稳定时间段中给料流量进行实时检测，结果如图5所示。由图5可知，等径等距螺旋给料的平均流量为0.67 kg/s，流量波动范围为0.56～0.75 kg/s，流量波动较大，波动范围为11.94%～16.42%，螺旋给料精度较小。

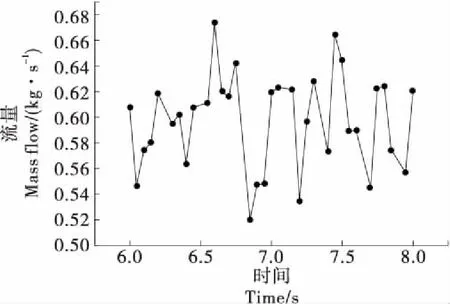
图5 质量流量检测图ⅠFigure 5 Mass flow detection diagram Ⅰ

2.2.6 变距螺旋流动状态分析 根据变距螺旋设计结果，将采用Solidworks建立的模型导入EDEM软件进行仿真，结果如图6所示。

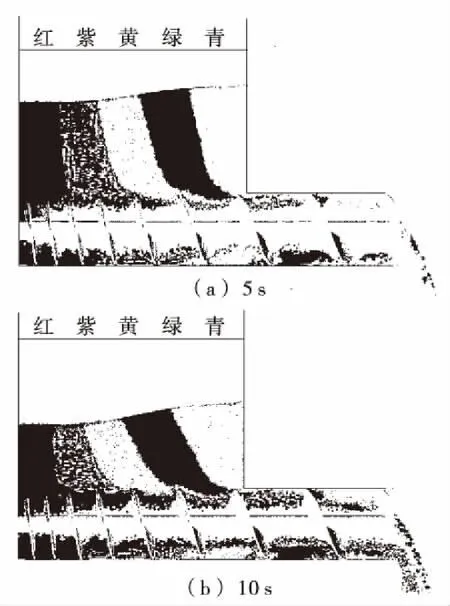
图6 变螺距仿真图Figure 6 Variable pitch simulation diagram

由图6可知，当仿真时间为5 s时，料斗中的色带下料相对平稳，5个色带相对较为垂直，其顶端形成轻微的倾斜滑移面，螺旋结构采用螺距逐渐增大及后段螺距与前段螺距差值逐步增加的原则，此时进料段中留有大量的白色物料，各色带的物料沿螺旋料筒的外力边缘被推进。当仿真时间为10 s时，料斗中的色带下料相对等距结构而言较为平稳，料斗中的红紫色带较为垂直，而黄绿青3个色带有向左下倾斜的趋势，5个色带的顶端形成轻微的倾斜滑移面，此时进料段中的白色物料还未完全推出，出口物料可观察到明显的无色带混合状态。

2.2.7 变距螺旋结构速度分析 与常规等距螺旋设定相同，采用三色模式，暗红、红、蓝速度大小依次递减，其速度分布如图7所示。由图7可知，当仿真时间为5 s时，第一圈螺距处有明显的红色物料，料斗顶端形成轻微滑移面，料斗中物料均逐渐向第一圈螺距滑动。当仿真时间为10 s时，其速度分布情况与5 s时的基本相似，料斗中物料速度下料均匀，进料段红色区域均匀分布。

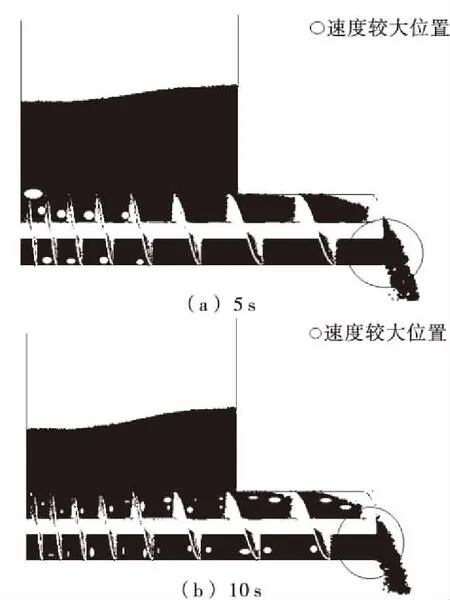
图7 变螺距速度分析图Figure 7 Analysis chart of constant pitch speed

2.2.8 变距螺旋给料流量分析 仿真后对变距流量进行检测，观察设计的变距螺旋结构给料流量波动情况，结果如图8所示。由图8可知，相对常规的等径等距螺旋结构，变距螺杆的平均给料流量为0.224 kg/s，流量值相对等距螺旋结构有所降低，主要是由于常规等距螺旋下料中，料斗物料形成明显的死区现象，物料均趋向于首圈螺距，在料斗中形成明显的滑移面，加之粉体形成坍塌现象，因粉体物料的较强压缩性，输送中粉体物料被压实导致填充率增大，流量增加；但输送不稳定，给料精度大大减小。变距螺杆的给料流量在时间段内同样呈波浪状，但波动相对较小，流量波动范围为0.207～0.239 kg/s，波动百分比在±6.69%以内。变距螺旋结构的设计方案在相同转速、管径等参数下，流量相对常规等距螺旋会有所降低，但实际中可通过提高转速、管径等方法，在满足给料流量的前提下，使得给料精度大大提高。

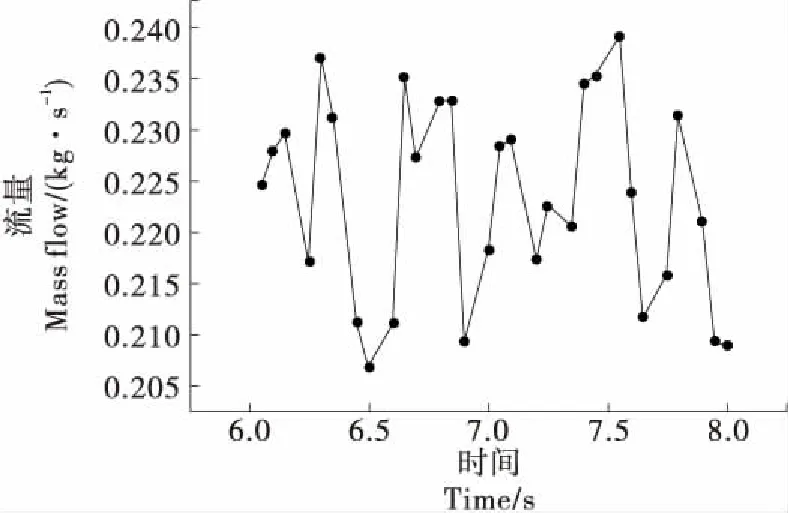
图8 质量流量检测图ⅡFigure 8 Mass flow detection diagram Ⅱ

3 结论

针对变距螺旋螺距随轴向x轴呈线性变化，建立了二次函数方程；根据坐标点选取，求得螺距与x的线性理论方程；根据设计要求，求得变距螺旋进料段各圈螺距值，为变距螺旋结构的设计计算提供了参考。变距螺旋结构离散元仿真结果表明，试验设计的变距螺旋结构相对等距螺旋下料均匀；变距螺旋螺杆的平均给料流量为0.224 kg/s，流量波动范围为0.207～0.239 kg/s，波动百分比在±6.69% 以内，相比常规等距螺旋结构，其给料精度较高，说明等径变距螺旋设计具有合理性。后续可搭建透明的螺旋料筒装置试验平台，验证离散元仿真结果的精确性。