基于核相关滤波与特征融合的分块跟踪算法

张灿龙,李燕茹,李志欣,2,王智文

(1.广西师范大学 广西多源信息挖掘与安全重点实验室，广西 桂林 541004；2.广西区域多源信息集成与智能信息处理协同创新中心，广西 桂林 541004；3.广西科技大学 计算机科学与通信工程学院，广西 柳州 545006)

目标跟踪是完成视觉监控[1-2]、人机交互[3-4]、车辆导航[5-6]、医学诊断[7-8]等诸多视频场景分析和理解任务的基础，其本质是在每帧图像中标记出目标的位置、大小和形状。目标模型的好坏是跟踪能否成功的关键，因此，按照目标建模方式将目标跟踪算法分为生成式模型[9]与判别式模型[10]这2类。生成式模型通过在线学习方式直接描述目标的观测，然后进行目标搜索，寻找样本与目标的联合概率，选择与目标模型最匹配的图像区域作为当前真实目标的估计来完成目标定位。生成式模型一般有基于核[11]、基于稀疏表示[12]等方法，其经典算法有粒子滤波[13]、mean-shift[14]、卡尔曼滤波[15]等。与生成式模型不同的是，判别式模型充分利用了目标和背景信息，将目标跟踪看作是一个目标前景和背景的二分类问题，通过计算其条件概率来判断是目标还是背景，从而降低算法的复杂度。目标的快速运动、遮挡、光照变化、背景混乱、运动模糊、大变化尺度等问题仍是目标跟踪当前所面临的主要挑战[16-17]。

近年来，基于相关滤波的跟踪方法被广泛研究，并取得了较好的效果。文献[18]最早将相关滤波应用到目标跟踪领域中，提出了最小平方和输出(minimum output sum of squared error，MOSSE)跟踪算法。MOSSE在空间域上的表达为带线性核的脊回归，因此，Henriques等[19-20]在脊回归中引入循环结构来增加样本，使用核技巧解决样本不可分问题，提出了循环结构的目标检测跟踪器(exploiting the circulant structure of tracking-by-detection with kernels，CSK)[19]和核化相关滤波跟踪算法(kernelized correlation filters，KCF)[20]，利用循环矩阵的循环结构和快速傅里叶变换对检测器的训练进行加速。Danelljan等[21]在CSK基础上，将RGB空间的图像映射到CN空间，对多通道颜色特征进行扩展，每个通道图像单独处理，然后利用PCA对特征进行降维，以此来提高算法实时性。另外，Danelljan等[22]还在MOSSE算法基础上增加一个尺度滤波，提出了一种判别性尺度空间跟踪器(discriminative scale space tracker，DSST)。

以上基于相关滤波的跟踪算法在速度和尺度变化上表现良好，但由于没有处理目标遮挡的机制，在目标产生遮挡时容易导致跟踪失败。文献[23]提出一种基于可靠分块的跟踪器(reliable patches trackers，RPT)来实现自动判断每帧目标的初始位置，该方法首先使用蒙特卡罗方法投票来选择可靠的块，然后使用核相关滤波器对每个可靠子块进行跟踪来得到当前帧目标的位置。由于蒙特卡罗滤波对目标模型和噪声没有限制，从而间接导致RPT的实时性较差，不能满足跟踪算法在速度上的要求。

上述基于相关滤波方法从不同方面来提升算法的跟踪性能，KCF和CSK等基本能实现实时跟踪，但是由于它们都使用单一特征进行目标表示，从而影响算法的跟踪精度。为此，本文以核相关滤波器为基础模型，提出一种多特征融合与目标自适应分块的跟踪算法。该算法首先对目标进行自适应分块，并对各子块提取HOG特征和CN特征进行融合；然后，在核相关滤波跟踪算法框架下，使用融合特征对各子块目标进行建模，得到各子块的最大响应位置；最后，通过对各子块的最佳响应位置进行加权平均来得到目标最终位置。此外，本文还提出一种自适应更新策略来处理有效子块。

1 核相关滤波跟踪算法

与大多数判别式跟踪算法相同，KCF在每一帧的跟踪中包括目标检测、训练2部分。在目标图像序列的第一帧中，用机器学习训练一个目标检测器来获得目标的中心位置，然后使用检测到的目标位置去预测下一帧目标的最优位置，最后使用检测结果来更新训练集，进而更新目标检测器。KCF方法使用循环矩阵进行样本采集，利用岭回归训练检测器，采用快速傅里叶变换对算法进行加速计算。在第t帧中，训练采用的损失函数为

(1)

式中：x是样本数据；y是回归目标；w是分类器权重系数；λ是正则化参数；f是分类函数；‖·‖为范数运算。在样本线性可分情况下，根据岭回归求解得

w=(XTX+λI)-1XTy,

(2)

式中：X是由样本数据循环移位构成的循环矩阵；y是由所有样本标签yi串联组成的高斯标签函数；I为单位矩阵。

式(2)在傅里叶域中写成

(3)

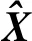
在实际情况下，样本大多是线性不可分的，为此引入核函数，将低维线性不可分样本映射到高维空间，使样本线性可分。其中核函数可表示为k(x,x′)=φT(x)φ(x′)，k(x,x′)为核函数，φT(x)和φ(x′)表示将低维特征空间中线性不可分的样本映射到高维特征空间的映射函数。利用核函数将低维线性不可分样本映射到高维空间后的样本权重组合为

(4)

式中αi是样本xi在非线性空间中对应的分量，即转化为求α的最小值。利用核函数理论[24]和岭回归得到式(4)的解为

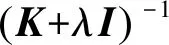
(5)

式中K为循环矩阵。由于式(5)中存在复杂的求逆过程，故将其转到傅里叶域中求解。α在对偶空间的解为

(6)

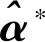
(7)

式中：F-1表示傅里叶逆变换；σ是高斯核函数的带宽。

在第t+1帧中，使用输入图像z作为计算傅里叶域中响应的基样本，根据式(4)将分类器响应输出表示为

(8)

式中：xi是模型的训练样本；z是检测区域。利用循环矩阵加快计算，得到第t+1帧的最终响应为

(9)

2 本文方法

针对跟踪过程中出现目标遮挡、形变等问题，本文在核相关滤波跟踪算法框架下，利用目标图像的大小和长宽比对目标进行自适应分块；对于每个子块，采用HOG和CN的多通道聚合特征对目标进行跟踪，得到各子块的最大响应位置；通过对各个子块的最大响应位置进行加权平均来获得最终的目标位置。对每个有效子块进行自适应模型更新，无效子块进行重新划分。本文提出的基于核相关滤波的块跟踪器(block tracker based on KCF，BKCF)的整体结构如图1所示。

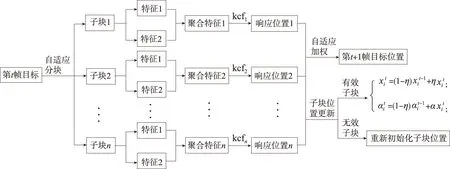
图1 BKCF算法结构Fig.1 BKCF structure

2.1 目标自适应分块

为了使目标被分割后所产生的每个子块的大小适中且变化不大，必须规定一个基准的目标尺寸。通过实验发现取基准值T1=900像素比较合适，并记实际目标图像的像素数与基准像素数T1之间的比值向上取整为δ。同时，为了使每个子块的外在高宽比尽可能与目标图像保持一致，本文将跟踪框的高宽比T2也作为自适应分块的重要依据。最终采取自适应分块方式为：当T2<1时，将目标水平方向均等分为3×δ块，垂直方向均等分为2×δ块，如图2(a)所示；当T2>1时，将目标水平方向分均等分为2×δ块，垂直方向均等分为3×δ块，如图2(b)所示；当T2=1时，在垂直和水平方向各等分为2×δ块，如图2(c)所示。

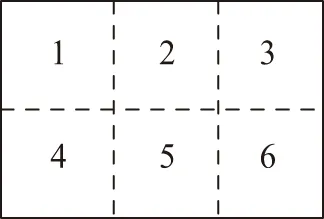
(a) T2<1,δ=1

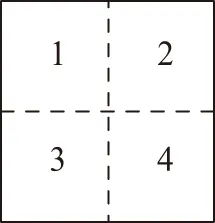
(c) T2=1,δ=1

2.2 子块特征提取与融合

目标特征是视觉跟踪的基础，目标跟踪利用目标特征来区分不同目标和目标定位，所以特征的选择至关重要，直接影响着算法的鲁棒性。目前相关滤波跟踪算法普遍采用灰度特征(Gray)、方向梯度直方图(HOG)[25]、颜色特征(CN)这3种特征。Gray特征建模计算比较简单，虽然提高了算法的时间鲁棒性，但由于其对目标的描述能力有限，从而导致跟踪精度不高。HOG特征主要是对目标的区域信息进行描述，通过计算和统计图像局部区域信息，有效保留目标的位置信息，具有光照不变性。KCF算法通过单独采用Gray或HOG特征进行对比实验，发现使用HOG作为目标特征的跟踪效果会更好。CN特征作为全局特征的一种，对目标有直观、快速的整体描述，是现有图像处理中常用特征。颜色模型通常使用个3个参数的三维坐标来描述特征，常用的颜色模型有RGB颜色空间、YUV颜色空间、YIQ颜色空间、HSV颜色空间等，其中最基础的是RGB空间。在实际运用中，颜色特征对光照敏感，当目标颜色与背景颜色相同或相近时会直接导致目标描述失败。基于HOG特征和CN特征两者的互补性，本节使用文献[25]的方法将RGB空间转换为CN空间[26]，并利用核函数多通道聚合方法对HOG特征和CN特征进行加权融合，得到融合特征。核函数选用高斯核函数

(10)

式中：xc是第c个通道HOG特征和CN特征的融合特征；σ为高斯核函数的带宽。

2.3 子块跟踪与目标定位

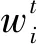
(11)

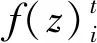
(12)

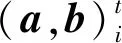
2.4 子块更新

在复杂场景下，跟踪目标容易被遮挡，如果不能及时更新目标模型就会造成跟踪漂移，从而导致目标丢失。为此，本节针对跟踪错误或被遮挡的子块提出了一种更新方式。在跟踪过程中，使用子块检测区域响应图的峰值旁瓣比(peak to side lobe ratio，PSR)来判断子块是否被遮挡，当PSR小于一定的阈值时就认为跟踪目标产生遮挡。子块的PSR计算公式为

(13)

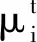
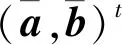
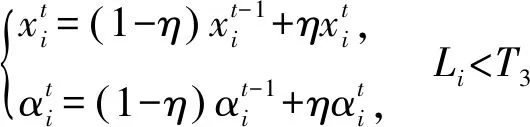
(14)

式中η是模板的学习速率，实验中取η=0.125。为确保子块的有效性和防过拟合的产生，T3的取值是关键，经过多次实验测试，T3的值取目标跟踪框对角线长度的一半时效果最优。

3 实验与分析

为了验证BKCF算法的鲁棒性，根据文献[27]提供的标准数据集中部分图像序列来测试BKCF算法[27]，数据集中图像序列的属性包括：光照变化(illumination variation，IV)、尺度(scale variation，SV)、遮挡(occlusion，OCC)、形变(deformation，DEF)、运动模糊(motion blur，MB)、快速运动(fast motion，FM)、平面内旋转(in-plane rotation，IPR)、平面外旋转(out-of-plane rotation，OPR)、超出视野(out-of-view，OV)、背景杂波(background clutters，BC)、低分辨率(low resolution，LR)。部分图像序列属性如表1所示。本章采用CSK、KCF、DSST和RPT这4种算法与BKCF算法进行定性和定量比较。实验平台环境为Windows 7操作系统，Intel Core(TM) i7-6700 3.40 GHz处理器，使用MATLAB R2014a编程实现。

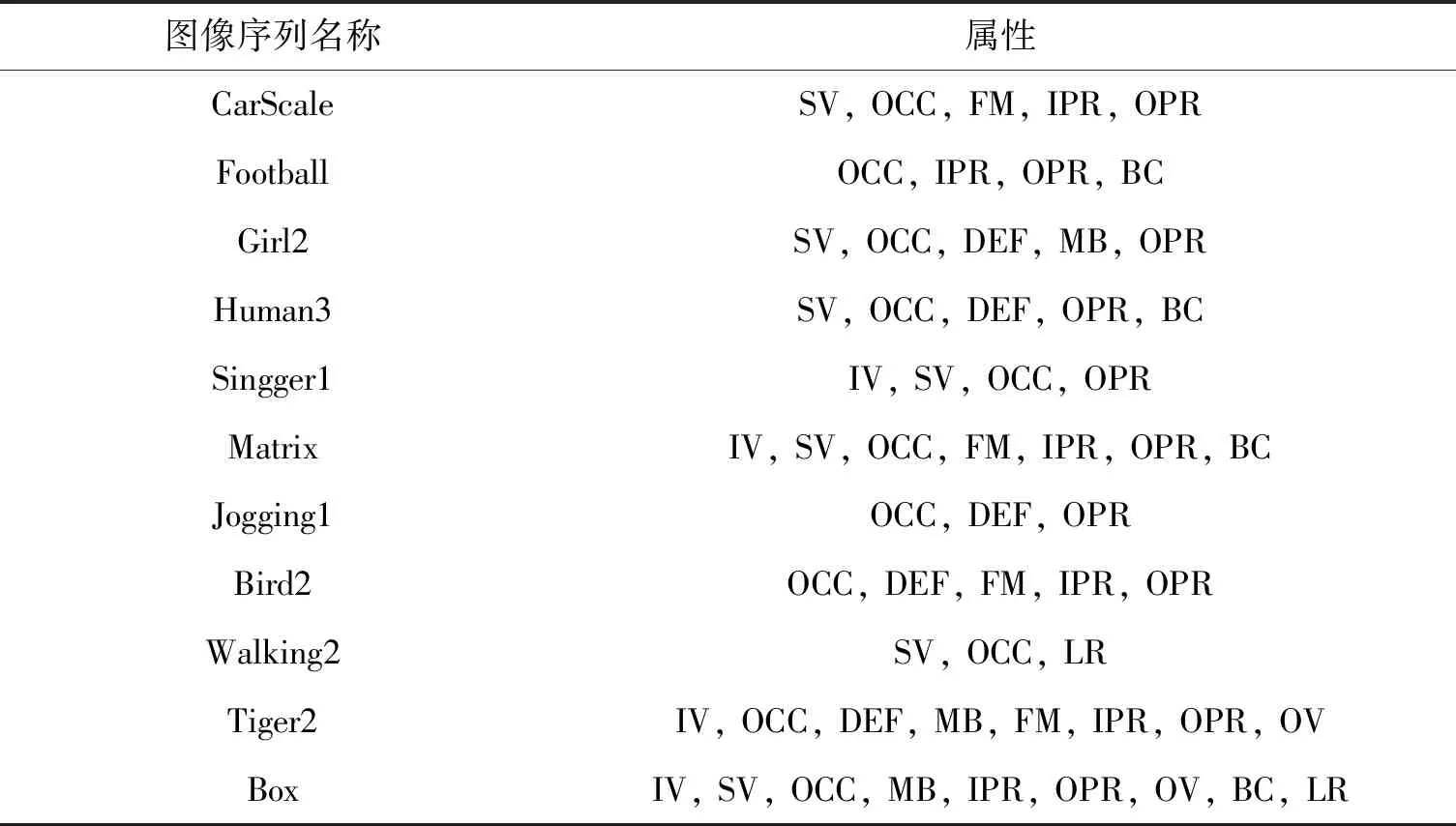
表1 部分测图像序列属性列表Tab.1 List of partial image sequence attributes

3.1 实验定性分析

为了验证BKCF算法在处理目标产生遮挡、尺度变化、快速移动、目标交汇等问题时的鲁棒性，选取Jogging1、Walking2等图像序列进行对比实验。图3给出了部分图像序列中对应帧号的跟踪结果。

3.1.1 遮挡实验

通过跟踪Jogging1、Human3等图像序列来测试当目标产生遮挡时算法的鲁棒性。在图3(a)和图3(c)中，目标行人的运动速度较为平缓，主要是目标行人在经过红绿灯杆时产生严重遮挡，如图3(a)所示，在第73帧之前，目标没有产生遮挡，BKCF与KCF等都能稳定地跟踪目标，第73帧后，目标被完全遮挡。当目标重现视野范围时，KCF、DSST等算法出现漂移或者直接丢失目标，但是BKCF仍然可以准确地标注出目标位置。在图3(c)中，目标行人在与其中一个行人靠近，产生遮挡后再通过红绿灯杆，产生二次遮挡后，KCF等算法的目标模型都产生漂移，BKCF通过对判断为遮挡的无效子块进行重采样来减小遮挡问题给算法带来的影响，因此当目标产生遮挡时，BKCF仍可以鲁棒地跟踪目标。

3.1.2 目标快速移动实验

利用Box和Matrix展示背景杂波、目标快速移动、光照变化时的跟踪结果。在图3(b)中，目标的分辨率偏低，且与背景的某些区域相似，在第454帧之前，除了CSK之外的算法，目标都能较稳定地被跟踪，在第479帧时，目标向下移动产生局部遮挡，且目标本身颜色与其附近背景及其相近，4种算法都能捕抓到目标。在第500帧时，目标位置向右移后，可以明显看到 CSK、KCF、DSST都跟踪失败，RPT和BKCF能较好地跟踪到目标。

在图3(d)中，由于Matrix图像序列属性较多，CSK和KCF最先出现跟踪漂移。在第13帧时，DSST、RPT和BKCF算法都能较好地跟踪到目标，在第36帧到第37帧之间，目标快速从上方移动到了下方，且目标部分被手臂遮挡住。针对这种情况的产生，DSST和RPT由于缺少对应的模型更新策略，无法适应目标快速移动，从而导致算法失效，BKCF算法针对子块模型更新提出了一种新的更新策略，能对目标进行有效地捕获。

3.1.3 尺度变化实验

利用Walking2和CarScale图像序列测试目标尺度产生变化时BKCF、CSK、KCF、DSST、RPT的跟踪性能。在图3(e)中，目标沿走廊一直向前走，目标尺度逐渐变小，在第197帧时产生遮挡，各算法均能实现对目标准确跟踪。在第387帧时，CSK、KCF和RPT算法虽然能捕捉到目标，但是它们的跟踪窗尺寸无明显变化，并且目标在缩小的同时算法的检测区域并没有改变，导致整个检测区域中背景像素增加，从而影响算法的鲁棒性。DSST算法和BKCF算法在此图像序列测试中能稳定地跟踪目标。在图3(f)中，与图3(e)情况相反，随着帧数的推移，目标跟踪车辆从远到近，尺度逐步增大，在第157帧时目标尺寸是第60帧的2倍，第197帧时目标尺寸是第60帧的3.5倍，BKCF仍然可以有效地跟踪目标。

图3 各算法的目标跟踪结果Fig.3 Tracking result of each algorithm

3.1.4 相似目标靠近与目标交汇实验

利用Football图像序列测试相似目标靠近与目标交汇时BKCF、CSK、KCF、DSST、RPT的跟踪性能。如图3(g)所示,在第117帧时目标球员靠近背景球员，发生交汇现象，除CSK算法发生了漂移以外，其余算法基本能成功跟踪目标。在第124帧和第131帧跟踪结果中，可以明显发现CSK、KCF、DSST算法的跟踪结果产生了漂移，原因是CSK、KCF、DSST算法都是使用单一特征，当目标与相似背景发生重叠时，算法无法正确判断出该区域是目标还是背景，导致检测结果会被目标附近的背景目标吸引，从而使目标跟踪发生偏移。本文的BKCF算法通过循环采样，利用多通道技术融合HOG特征和CN特征，并使用融合后的特征来对目标和背景进行正负样本分类，所以出现目标交汇的现象时，仍能稳定地跟踪目标。

3.2 实验定量分析

定量分析采用中心误差、重叠率和帧率(frame per second,FPS)作为评价指标。设人工标注的目标真实位置中心坐标为(xtrue,ytrue)，跟踪算法在跟踪过程中输出结果的中心位置为(xG,yG)，γtrue和γG分别为人工标注的边界框和跟踪结果的边界框。则：

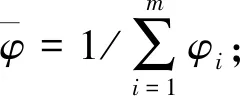
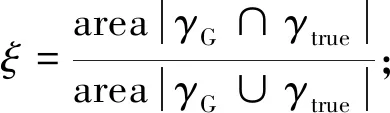
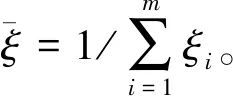
式中：m为图像序列总帧数；|·|为目标区域内像素点个数；∩和∪分别为2个边界框所构成区域的交集和并集。中心误差越小，跟踪精度越高，重叠率越高，跟踪结果越可靠。

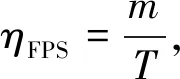
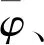
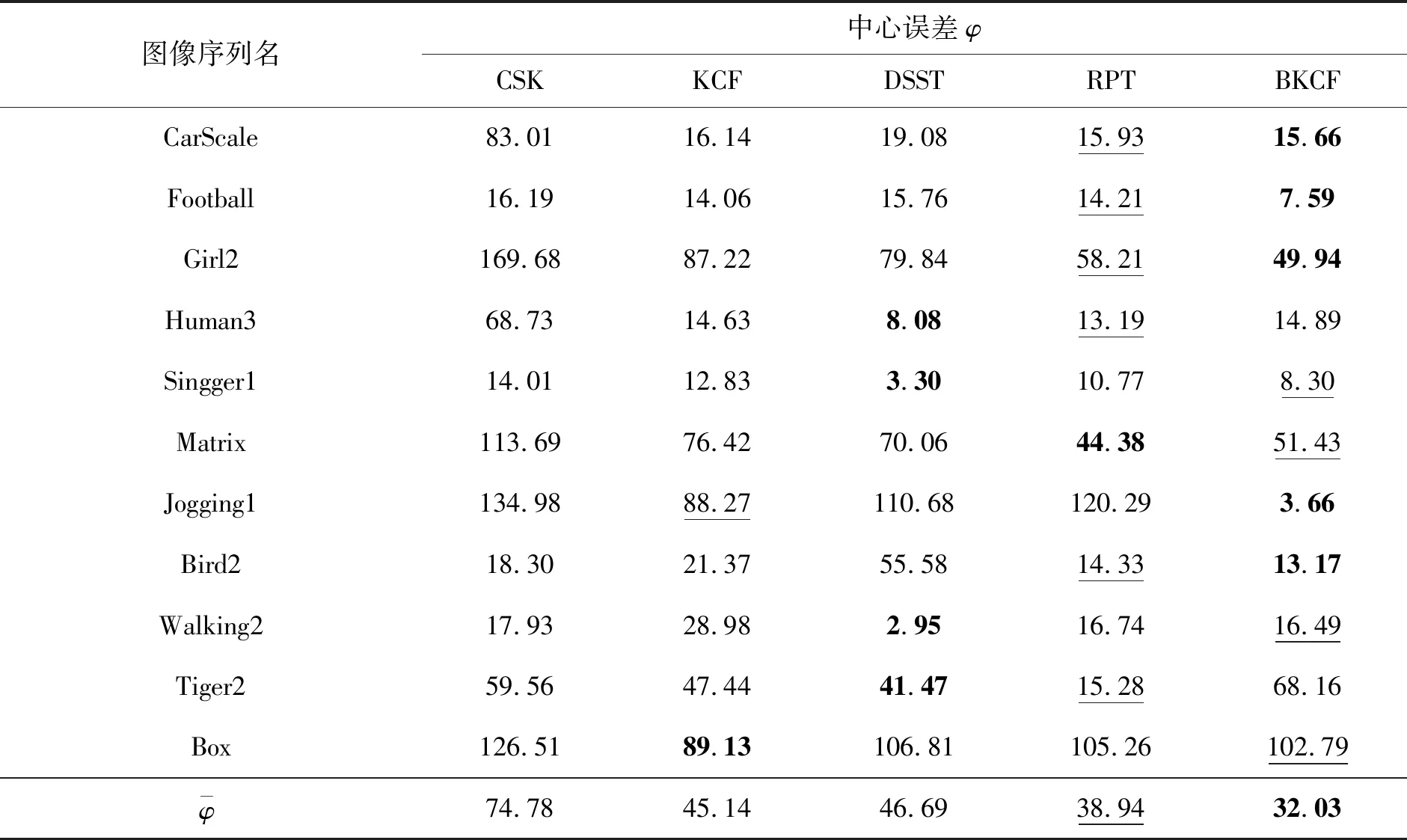
表2 各算法在11个图像序列的跟踪精度Tab.2 Tracking accuracy of each algorithm in 11 image sequences

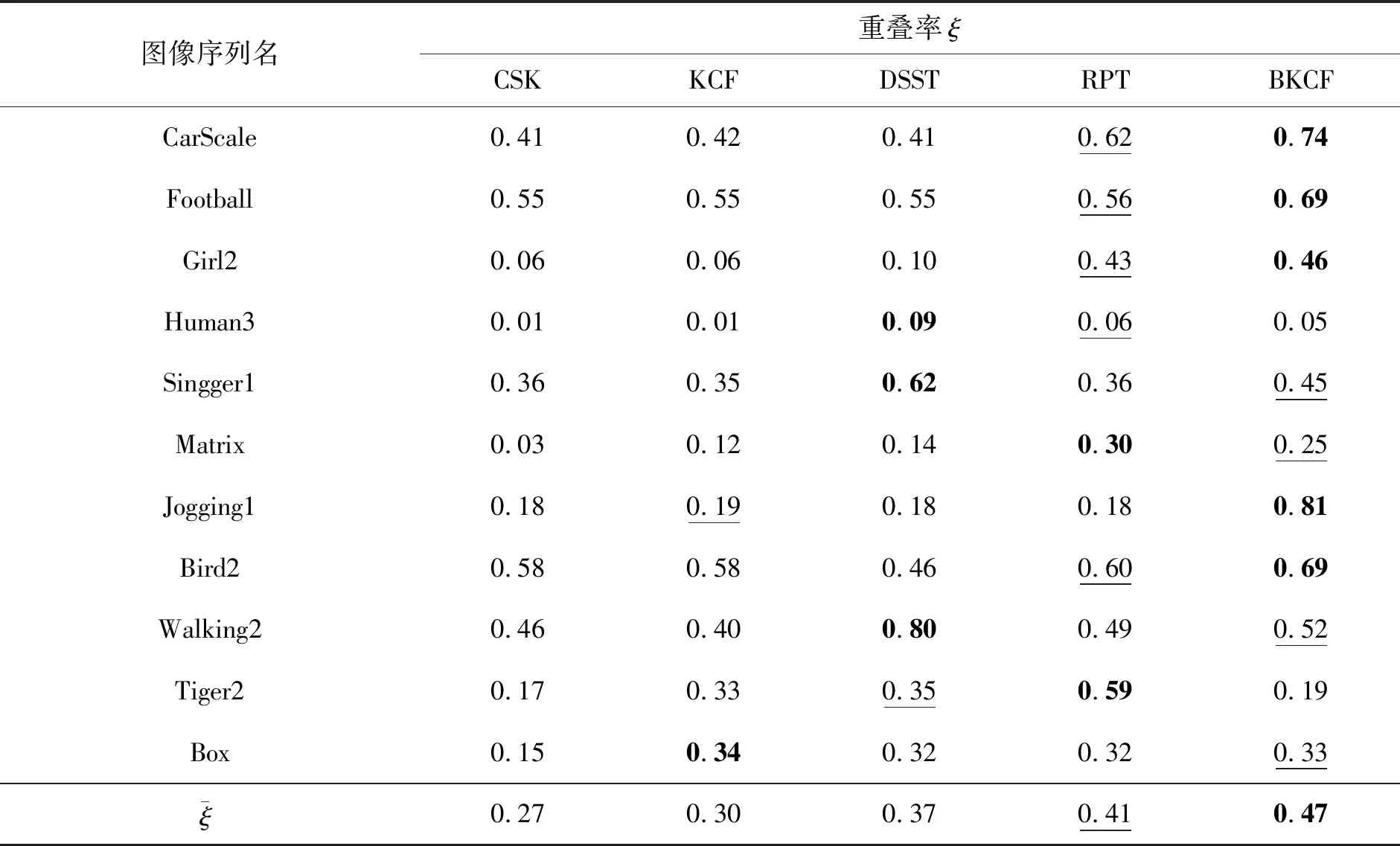
表3 各算法在11个图像序列的跟踪成功率Tab.3 Tracking success rate of each algorithm in 11 image sequences

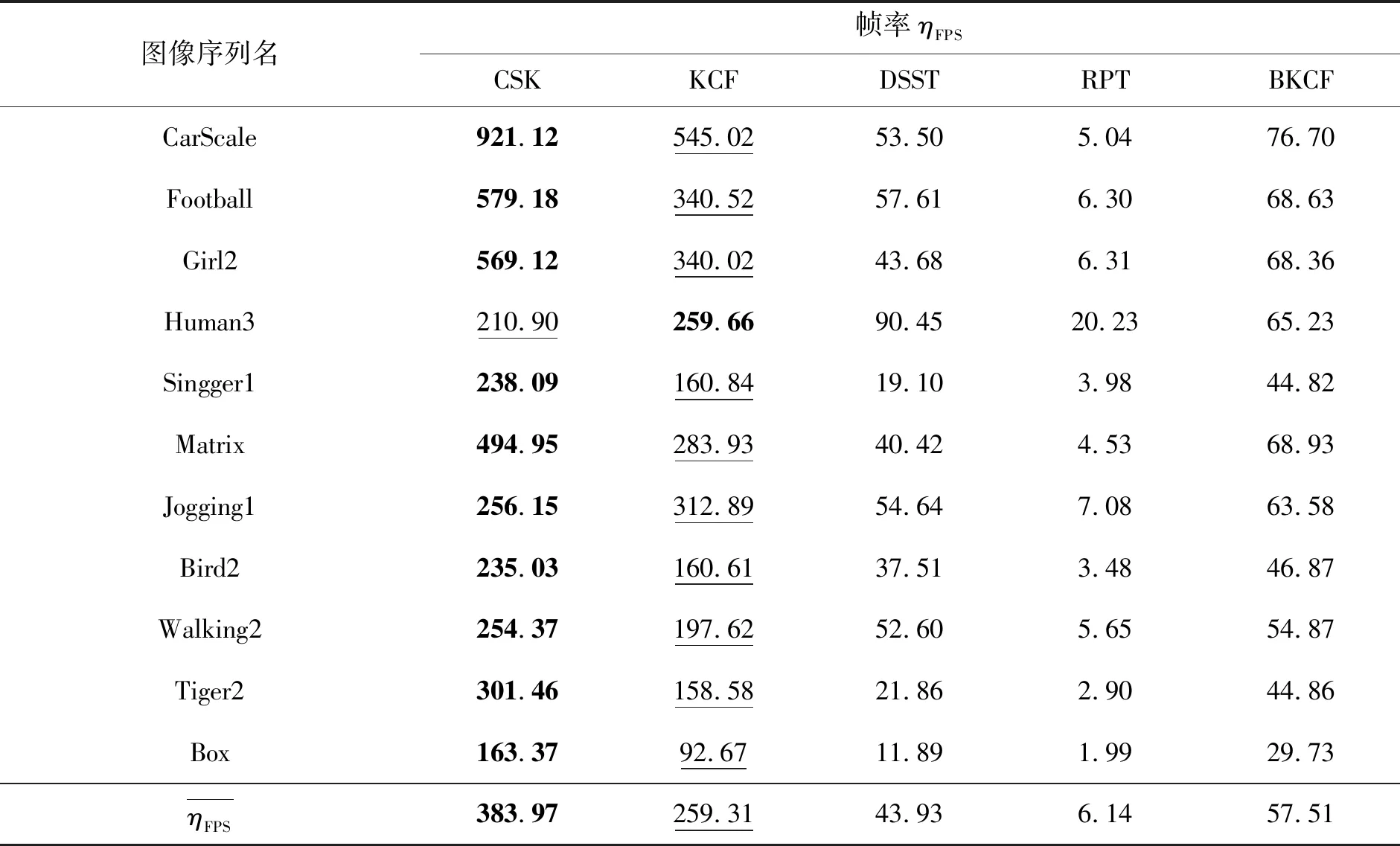
表4 各算法在11个图像序列的跟踪速度Tab.4 Tracking speed of each algorithm in 11 image sequences

在算法实时性方面，加入了平均帧率评判标准。BKCF在KCF基础上添加了分块和特征融合机制，增加了算法的复杂度。从表4中可以看，随着帧数的增加，BKCF的平均帧率虽然降低了，但是相比于DSST和RPT，仍能够保持在每秒57帧，基本满足实时要求。表5为各跟踪方法在11个图像序列的各个属性上的平均跟踪精度。从表5可以看出，BKCF算法在处理遮挡、形变、旋转等影响因素上的平均跟踪精度较高，但因为CN特征对光照较敏感，BKCF算法在处理光照变化问题时跟踪效果稍弱。

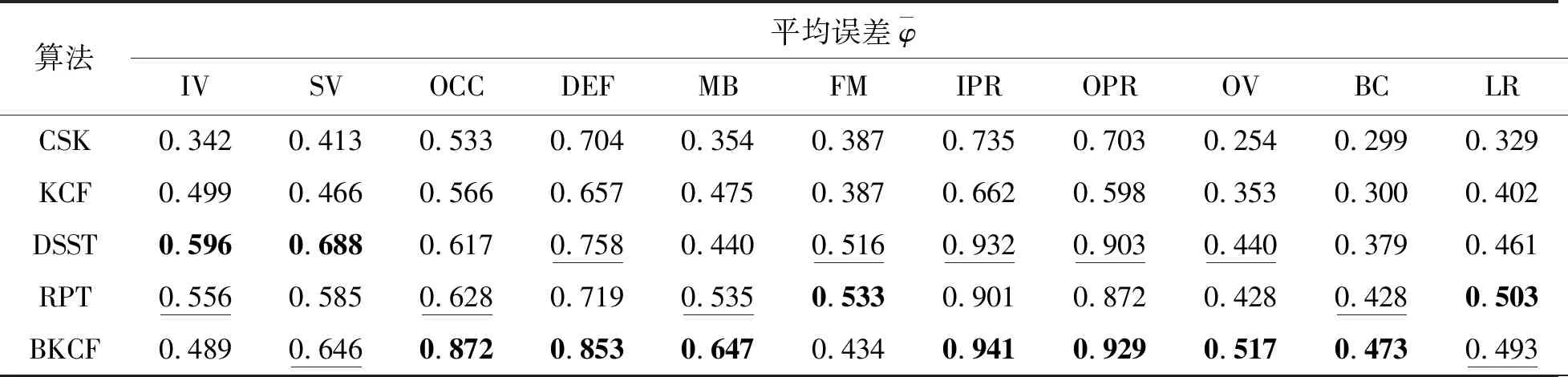
表5 各算法在11个图像序列属性的平均精度Tab.5 Average accuracy of each tracking algorithm in 11 image sequence attributes

图4和图5为BKCF算法与其他4种算法在11组实验的定性分析，其中图4是11组实验各跟踪算法的准确率，图5是11组实验各跟踪算法的成功率。综合图4和图5可得：BKCF跟踪算法的跟踪准确率和成功率高于CSK、KCF、DSST和RPT。相比于采用单一特征中效果最好的KCF，BKCF使用的是HOG和CN特征融合来表示目标，准确率和成功率分别提高了15.9和7.5个百分点，这表明特征的选择对于算法鲁棒性的重要性。RPT利用蒙特卡罗投票机制对子块目标进行可靠性判断，但蒙特卡罗滤波实时性较差，从而间接导致RPT不能满足速度上的要求。BKCF算法采用较简单的分块方式，利用KCF对子块进行跟踪，对无效子块进行重采样。相比于RPT，BKCF算法的准确率和成功率分别提高了10.2和6.5个百分点。

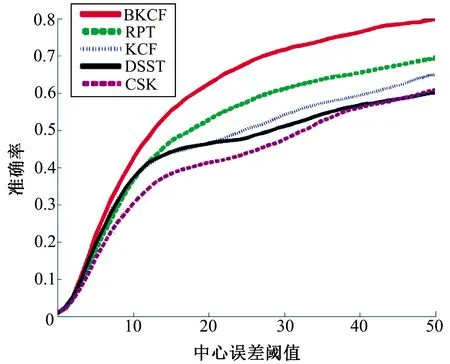
图4 5种跟踪算法的准确率Fig.4 Accuracy of 5 tracking algorithms

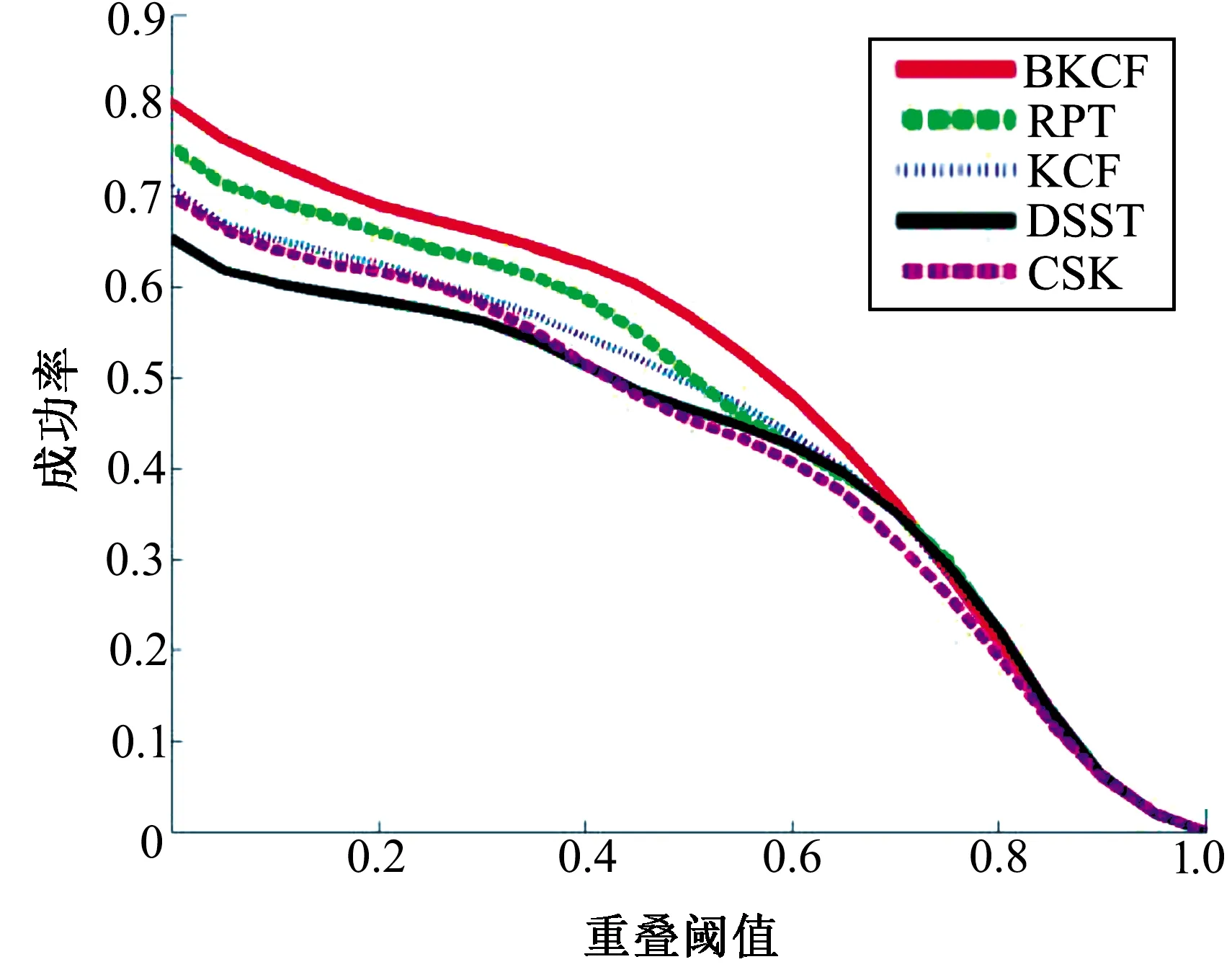
图5 5种跟踪算法的成功率Fig.5 Success rate of 5 tracking algorithm

4 结语

针对目标跟踪过程中产生遮挡、尺度变换等问题，本文在KCF算法的基础上提出了一种融合多特征与区域联合目标跟踪算法。实验结果表明BKCF算法在满足实时跟踪速度的要求下，在一定程度上提高了对尺度变化、遮挡等问题的处理能力。今后研究工作：将BKCF算法模型与深度学习网络模型结合，寻找适合的深度学习网络模型，对目标提取深度特征；探索更有效的目标划分和特征融合策略，建立更高效的模型，从而提高跟踪算法的精度。