三种群捕食-竞争-合作混杂模型的全局渐近稳定性

郑 涛,周欣然,张 龙

(新疆大学 数学与系统科学学院,新疆 乌鲁木齐 830046)

Lotka-Volterra种群模型在描述不同生物种群之间的相互关系之中扮演着重要的角色,这些模型包括捕食模型、竞争模型和合作模型。生物种群彼此之间经常会为了有限的资源呈现相互捕食、竞争、合作的关系[1-6]。但是在现实环境中,许多物种之间的关系并不是单一的,而是要相对复杂一些。当生物种群周围的环境发生变化时,种群之间的相互关系也会发生相应调整。比如，3个种群之间的捕食-竞争关系与捕食-合作关系的相互转化。本文不同于前人对于种群间单种关系的研究,我们对于3个种群之间存在的捕食-竞争关系与捕食-合作关系随时间做交替地周期变化的两类模型合并成一类三种群的捕食-竞争-合作混杂模型进行研究,讨论这样的系统下正平衡点的全局渐近稳定性[7-13]。

1 模型

具有时间周期的三种群捕食-竞争-合作混杂模型：

(1)

这里x和y是两食饵种群密度,z是捕食者种群密度,其中z种群同时捕食x和y两种群,x和y两种群之间存在随时间变化的相互关系,当时间t∈[2kτ,(2k+1)τ],种群x和种群y为相互竞争关系;当时间t∈[(2k+1)τ,(2k+2)τ],种群x和种群y为相互合作关系。其余各系数皆为正数。

为了方便研究,可以将式(1)合并为：

(2)

式中各系数为：

式中n∈N,各系数皆为正数。

2 正性与有界性

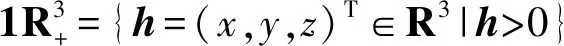
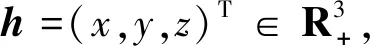
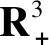
为了讨论方便,系统(2)可以写成矩阵形式

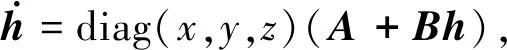
式中：

(3)

在讨论系统(2)解的有界性之前,先引进定义1。

定义1设Q为实矩阵,如果存在一个正的对角矩阵W,使得WQ+QTW是正定的,则称Q∈SW。

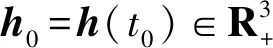
证明由于-B∈SW,所以存在正的对角矩阵

W=diag(ω1,ω2,ω3),ωi>0,i=1,2,3,

使得W(-B)+(-B)TW是正定的。

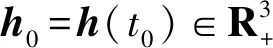
S(t)=ω1x+ω2y+ω3z。

那么由微分方程的比较原理[7]有

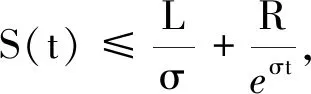
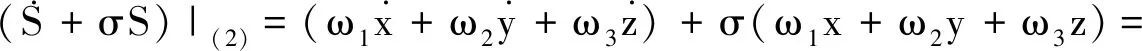
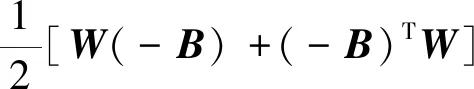
式中所有的二次项系数都为负,从而一定存在正数L,使得

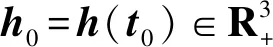
3 正平衡点的全局渐近稳定性

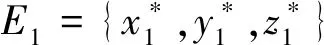
(4)

式中正平衡点为：

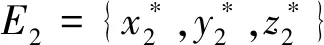
(5)

式中正平衡点：

设E={x*,y*,z*}为系统(2)的正平衡点,即E满足：

(6)

式中

正平衡点：

下面给出正平衡点E全局渐近稳定性的条件。

定理2若系统(2)满足条件-B∈SW,且

(7)

则其正平衡点全局渐近稳定。

证明定义Lyapunov 函数

式中ωi>0,i=1,2,3为待定常数。

沿着系统(2)的正解对V(h)求关于t的导数有

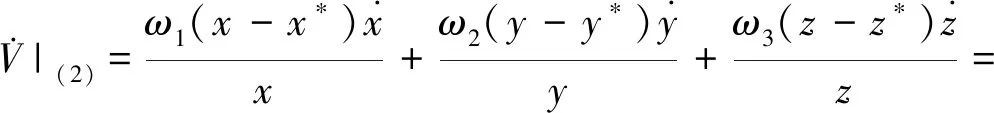
ω1(x-x*)(a1-b1x*+b1x*-c1z*+c1z*-d1y*+d1y*-b1x-c1z-d1y)+

ω2(y-y*)(a2-b2y*+b2y*-c2z*+c2z*-d2x*+d2x*-b2y-c2z-d2x)+

ω3(z-z*)(a3-b3z*+b3z*-c3x*+c3x*-d3y*+d3y*-b3z+c3x+d3y)=

ω1(x-x*)[b1(x*-x)+c1(z*-z)+d1(y*-y)]+

ω2(y-y*)[b2(y*-y)+c2(z*-z)+d2(x*-x)]+

ω3(z-z*)[b3(z*-z)+c3(x-x*)+d3(y-y*)]=

-b1ω1(x-x*)2-b2ω2(y-y*)2-b3ω3(z-z*)2+

(ω3c3-ω1c1)(x-x*)(z-z*)+(ω1d1+ω2d2)(x-x*)(y*-y)+

(ω2c2-ω3d3)(y-y*)(z*-z)≤

在此取定ω1=ω2=ω3=1,并利用式(7),则有

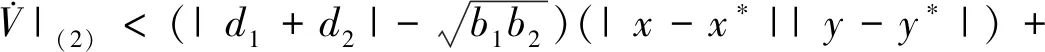
因此正平衡点E是全局渐近稳定的。证毕。

4 数值模拟

通过MATLAB软件进行数值模拟,验证该系统正平衡点具有全局渐近稳定性。在此取定相应系数值：

由此容易验证

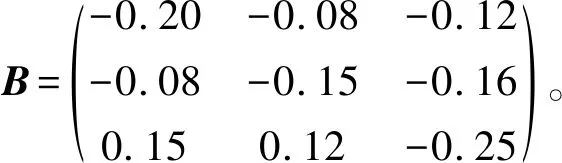
-B∈SW,且式(7)成立。

模拟1捕食-合作阶段和捕食-竞争阶段都满足式(7)时，分别模拟出系统(2)中x、y、z三种群密度随时间变化的时间序列与三维空间相。

图1、2中的解曲线分别代表系统(2)的初始值(x0,y0,z0)取定为(2.5,2.2,5.0),(2.8,2.4,4.8),(3.0,2.7,5.5),(3.4,2.5,5.2)的种群x、y、z的种群密度的时间序列与三维空间相。

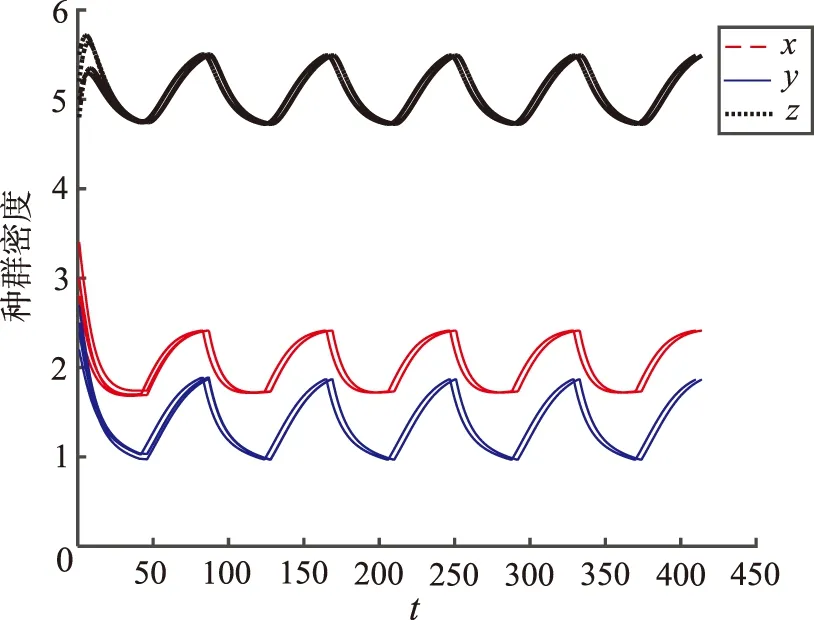
图1 模拟1的时间序列Fig.1 Time series diagram of simulation 1

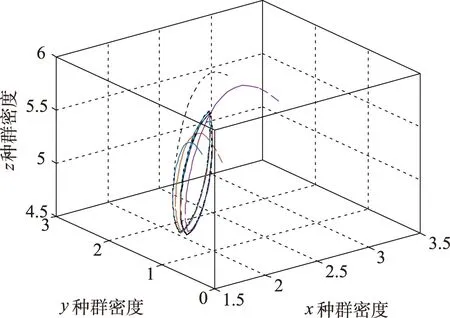
图2 模拟1的三维空间相Fig.2 3D phase diagram of simulation 1

模拟2取定一组相关系数使得2个阶段中的捕食-合作阶段满足式(7),然而捕食-竞争阶段不满足式(7),则模拟结果为图3和图4。

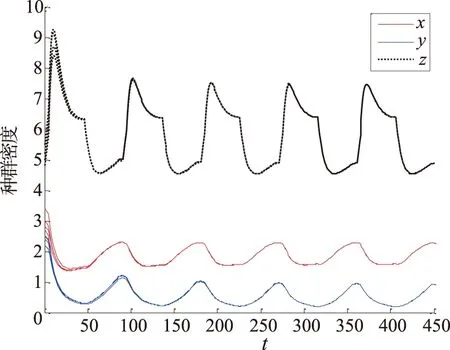
图3 模拟2的时间序列Fig.3 Time series diagram of simulation 2

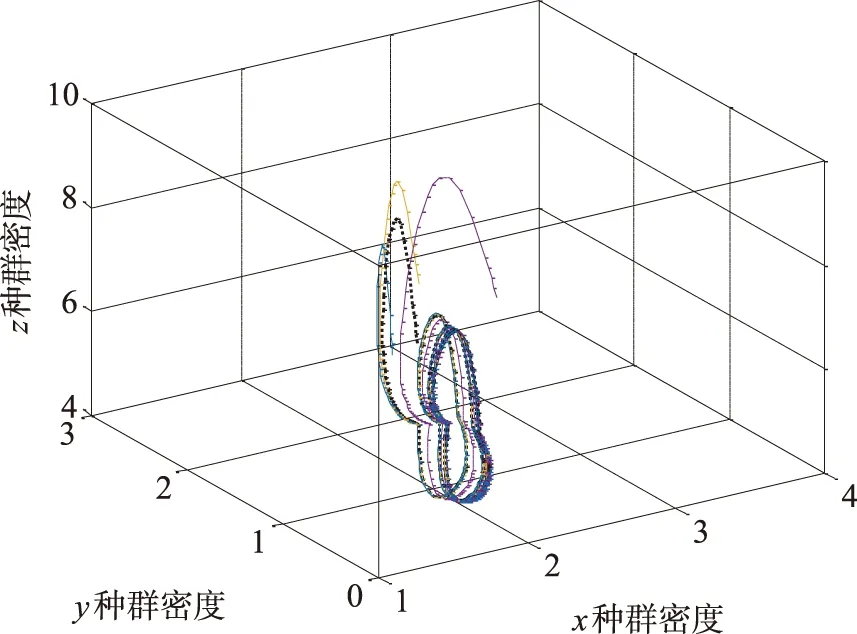
图4 模拟2的三维空间相Fig.4 3D phase diagram of simulation 2

图3、4中的解曲线分别代表系统(2)的初始值(x0,y0,z0)取定为(2.5,2.2,5.0),(2.8,2.4,4.8),(3.0,2.7,5.5),(3.4,2.5,5.2)的种群x、y、z的种群密度的时间序列与三维空间相。

模拟3取定一组相关系数使得2个阶段中的捕食-合作阶段与捕食-竞争阶段都不满足式(7),则模拟结果如图5、6。

图5、6中的解曲线分别代表系统(2)的初始值(x0,y0,z0)取定为(2.5,2.2,5.0),(2.8,2.4,4.8),(3.0,2.7,5.5),(3.4,2.5,5.2)的种群x、y、z的种群密度的时间序列与三维空间相。

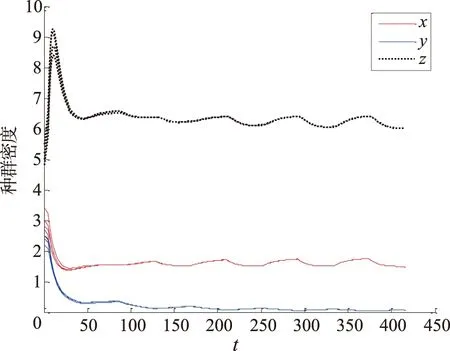
图5 模拟3的时间序列Fig.5 Time series diagram of simulation 3

由模拟出的图像可以看出,图1中的x、y、z3个种群密度随时间呈现反复交替的周期变化,并且三者的种群密度三维空间相图最终构成了一个闭合的图像,由此可以看出,系统(2)的正平衡点E=(x*,y*,z*)构成了一个周期的闭轨。图2两个阶段中若单个阶段满足条件式(7)，依旧能构成一个周期的闭轨,然而图3中2个阶段都不满足式(7),可以看到其中有一个食饵种群最终灭绝了,并且得不到周期的闭轨。

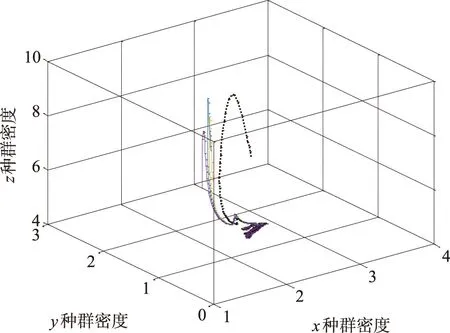
图6 模拟3的三维空间相Fig.6 3D phase diagram of simulation 3

5 结论

本文通过将3个种群之间的捕食-竞争与捕食-合作关系随时间周期变化的两类模型合并成一类三种群的捕食-竞争-合作混杂模型,讨论该模型下的系统解的正性、有界性,给出了系统正平衡点全局渐近稳定性的充分条件,证明了正平衡点的全局渐近稳定性。最后通过数值模拟检验了这一结论,并给出了若2个阶段中单个满足这一充分条件下的数值模拟。