基于Skew-t-GJRGARCH(1,1)模型的5G板块风险度量研究

李世君,唐国强,杜诗雪

(桂林理工大学 理学院，广西 桂林 541006)

2017年12月21日，在国际电信标准组织3GPP RAN第78次全体会议上，5G NR首发版本正式冻结并发布。2018年2月23日，沃达丰和华为完成首次5G通话测试。北京时间2018年8月3日，美国联邦通讯委员会(FCC)发布高频段频谱的竞拍规定，这些频谱将用于开发下一代5G无线网络。截至2018年12月12日,A股5G概念股共有143家，总市值达到14 540.23亿元，流通市值前5位分别是中国联通、中兴通讯、立讯精密、亨通光电、烽火通信。股市作为经济发展的晴雨表，5G板块指数一定程度上代表了5G行业的发展，因此对5G板块指数进行风险度量研究是很有意义的。

对国内外文献的分析研究发现，以往研究多是基于正态分布、t分布、GED分布等，很少选择有偏类型的分布，且对5G板块风险度量的文献较少，金融数据大多是不对称分布。因此，本文基于skew-t分布的 GJRGARCH(1,1)模型对5G板块进行风险度量研究，以期为投资者决策提供有效的帮助。

本文结构安排如下：第1章是理论模型介绍；第2章就5G板块进行风险度量研究；第3章是结论。

1 理论模型介绍

1.1 GJRGARCH模型

GJRGARCH模型是Glosten等[16]于1993年提出的，用于衡量利好消息或利空消息对条件方差的冲击，检验其是否具有杠杆效应。GJRGARCH模型如下：

rt=μt+at，

(1)

at=σtεt，

(2)

(3)

1.2 skew-t分布

Fernandez等[17]提出了skew-t分布，可以更好地捕捉偏度和尖峰厚尾特征。skew-t分布的对数似然函数如式(4)所示：

(4)

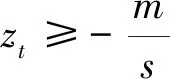
1.3 VaR的定义及计算

令rt是对数收益率序列在时刻t的观察值，[t,t+h]期间的损失为Lt+h=-(rt+h-rt)=Δr(h)，FL(x)=P(L≤x)是损失函数的累积分布函数。VaR在显著性水平α(常取1%和5%)下的值实际上就是FL分布函数的α分位数，换句话说，VaR表示满足不等式FL(x)≥α的最小实数，即

VaRα=inf {x|FL(x)≥α}。

(5)

在多头交易头寸的情况下，当交易资产价格下降时，损失风险就会产生；而在空头交易头寸的情况下，当资产价格上升时，风险就会产生。因此，分布的左右尾部分别为多头和空头位置建模。我国股市不允许做空机制，所以仅考虑多头位置建模。

如果序列εt是具有标准正态分布的随机变量,那么条件分布的5%分位数表示95%置信度下的VaR估计值，计算如下

(6)

如果序列εt是具有学生t分布的随机变量，自由度为ν，那么条件分布的5%分位数是

(7)

如果序列εt是具有skew-t分布的随机变量，自由度为ν，那么条件分布的5%分位数是

(8)

如果序列εt是具有ged分布的随机变量，自由度为ν，那么条件分布的5%分位数是

(9)

如果序列εt是具有skew-ged分布的随机变量，自由度为ν，那么条件分布的5%分位数是

(10)

1.4 Kupiec检验

假定计算VaR的置信度为c，实际考察天数为T,失败天数为N，则失败频率为p(N/T)。零假设为p=p*。这样对VaR模型的准确性评估就转换为检验失败频率p是否显著不同于p*。

Kupiec[18]给出了对零假设p=p*最合适的检验是似然比检验，即

TLR=2ln [(1-N/T)(T-N)(N/T)N]-2ln [(1-p)(T-N)pN]。

(11)

在零假设的条件下，统计量TLR服从自由度为1的χ2分布。

2 5G板块的风险度量研究

2.1 数据来源及预处理

本文选取5G板块指数(885556)2014年5月13日至2018年11月30日的日收盘价作为研究样本，共1 113个交易数据，数据来源于同花顺。采用日对数收益率进行分析，日对数收益率定义为rt=lncpt-lncpt-1，cpt为第t日的收盘价。研究结果由R软件和Eviews软件得出。

2.2 描述性统计与平稳性检验

5G板块指数日收盘价走势和5G板块指数日对数收益率时序分别如图1和图2所示。

图1 5G板块指数日收盘价走势Fig.1 5G sector index daily closing price chart

图2 5G板块指数日对数收益率时序Fig.2 5G plate index daily logarithmic rate of return timing chart

由图1可以看出，5G板块指数收盘价走势上下起伏较大，有2次大幅度的上升和下降，明显不是平稳序列。由图2可以看出，日对数收益率在0值附近波动，波动幅度在-0.10至0.10，存在波动聚集现象，大幅波动后面是大幅波动，小幅波动后面是小幅波动。

易知5G板块日对数收益率均值为0.000 4；标准差为0.026 9；偏度为-0.747 7，分布呈左偏；峰度为5.896 7，大于3，分布呈现尖峰厚尾特征；J-B统计量值为492.390 0；其对应的p值为0；拒绝收益率序列服从正态分布的原假设；日对数收益率序列ADF平稳性检验的p值为0.01，即认为序列是平稳的；日对数收益率白噪声检验的p值为0，拒绝序列为白噪声的原假设；DF值为-10.57；滞后阶数为10；卡方值为17.34；自由度为1。

综上可得，5G板块日对数收益率分布呈现左偏、尖峰厚尾、非正态、平稳非白噪声的特征。

2.3 ARCH效应检验

图3 平方序列的ACF和PACFFig.3 ACF and PACF plots for a square sequence

2.4 模型的参数估计

对rt可能服从的分布类型进行假设，假设分布包括正态分布(norm)、偏正态分布(skew-norm)、t分布(t)、偏t分布(skew-t)、广义误差分布(skew-ged)和偏广义误差分布(sged)，并通过AIC和BIC准则选出较优模型，模型比较结果如表1所示。

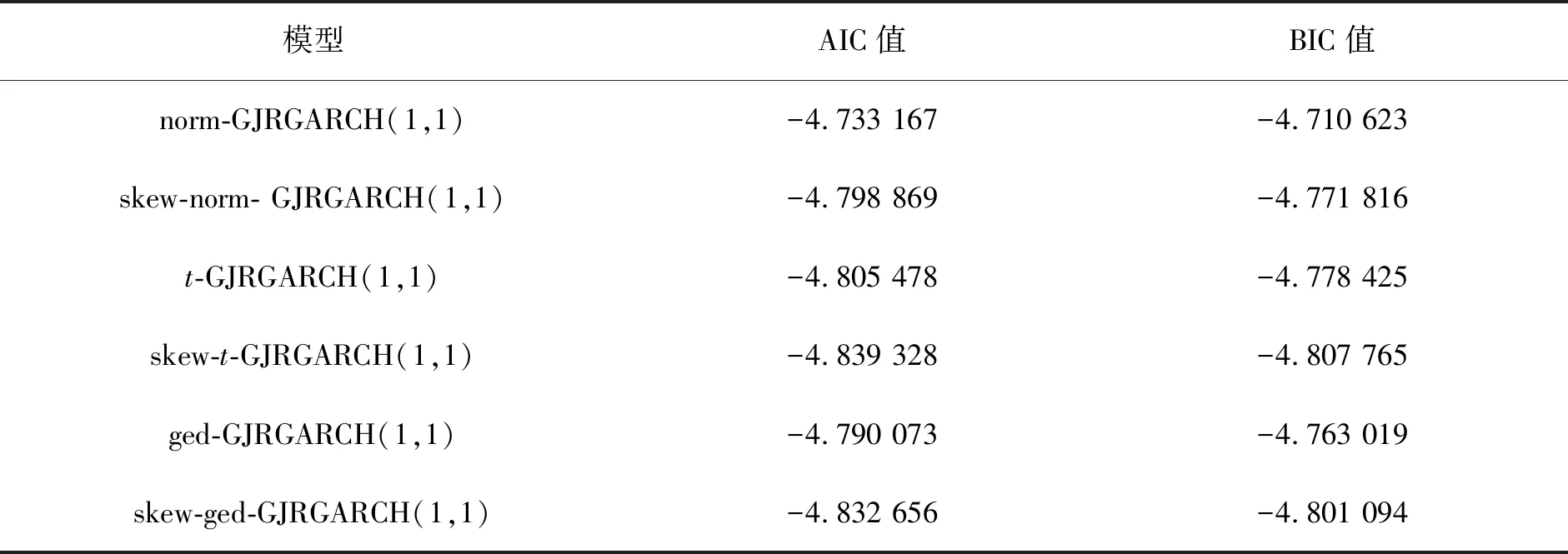
表1 各模型的信息准则Tab.1 Information guidelines for each model

由表1可得，有偏分布对应的 GJRGARCH(1,1)模型具有更小的AIC和BIC值，可以更好地刻画对数收益率序列的非对称现象。skew-t-GJRGARCH(1,1)具有最小的AIC和BIC值，为最优模型。接下来对有偏分布的3种 GJRGARCH(1,1)模型做参数估计，3种有偏分布模型的参数估计结果如表2所示。

表2 各模型的参数估计Tab.2 Parameter estimation of each model

上述3个模型的γ1值分别是0.004 106、0.001 647、0.000 305，几近于0，对应的p值分别是0.785 779、0.931 083、0.986 940，明显大于0.05，因此在5%的显著性水平下，不存在显著的杠杆效应，表明我国5G板块利空消息和利好消息造成的波动性并无显著差异。3个模型都是α1+β1<1,说明序列具有较强的持续波动性。通过表4的AIC和BIC值，以及表5的LogLikelihood值比较都可得出skew-t-GJRGARCH(1,1)模型是最优的。

图4给出了基于skew-t分布的GJRGARCH(1,1)模型所拟合的波动率和标准化残差的时序图，很好地表现了5G板块的特征，与图1、图2很好地形成对应。标准化残差的LB统计量为23.418，其对应的p值为0.268 7，消除了ARCH效应。

图4 skew-t-GJRGARCH(1,1)拟合的波动率和标准化残差Fig.4 Volatility and normalized residuals for skew-t-GJRGARCH(1,1) fitting

2.5 VaR的计算与Kupiec 检验

通过图5在置信水平95%下各时刻VaR值与实际值之间的相互关系，发现skew-t-GJRGARCH(1,1)模型预测的VaR值很好地表现出了收益率序列的时变特征，并且趋势一致。

图5 5G板块日收益率与skew-t-GJRGARCH(1,1)预测的VaR(95%)对比Fig.5 Comparison of daily yield of 5G plate and VaR (95%) predicted by skew-t-GJRGARCH(1,1)

表3 各模型的Kupiec 检验结果Tab.3 Kupiec test results for each model

3 结论

本文以5G板块指数为例：首先对收益率序列的基本特征进行描述；然后对杠杆效应进行研究；最后由AIC和BIC准则选择模型，比较 GJRGARCH(1,1)模型在不同偏态分布下对5G板块指数的VaR风险测度能力，并根据Kupiec 检验得到最优模型为skew-t-GJRGARCH(1,1)。从实证分析结果来看，基于skew-t分布的 GJRGARCH(1,1)模型可以很好地度量5G板块可能出现的最大损失，得到了5G板块不存在杠杆效应。市场监管者可以根据模型度量的结果来制定方针和策略，以应对突如其来的金融风险，更好地保护投资者。