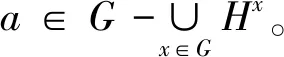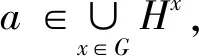自中心化子群对有限群结构的影响

孙雨晴，卢家宽

(广西师范大学 数学与统计学院，广西 桂林 541006)

设G是有限群，H是G的子群，若CG(H)≤H，则称H是G的自中心化子群。由于G本身是G的自中心化子群，故任何群都有自中心化子群。在文献[1]中，可以看到某些子群的中心化子对有限群的结构有很强的控制作用，自然想到能否通过自中心化子群的相关性质来刻画有限群的结构？答案是肯定的。例如：Mahmoud等[2]研究了自中心化子群都是正规子群的有限群，并得到了一些结果；Aivazidis等[3]研究了极大交换正规子群都是自中心化子群的有限群。另一方面，通过有限群的特殊子群的共轭类个数来刻画群结构，亦是群论研究者感兴趣的课题，例如：Belonogov[4]研究了极大子群的共轭类个数为3的有限群，并给出了非正规极大子群的共轭类个数不超过2的有限群的结构；周志浩等[5]对非交换子群共轭类个数为2的有限群进行了完全分类。钟祥贵等[6]研究了非次正规子群共轭类数对有限群结构的影响，并得到一些结果。相关的研究还有很多，并都取得了较好的结果，具体参考文献[7-9]。本文沿着上述研究，讨论自中心化子群都是C-正规子群的有限群，以及自中心化子群的共轭类个数对有限群结构的影响。

设G是有限群，F(G)是G的Fitting子群，F1(G)=F(G),F2(G)/F1(G)=F(G/F1(G))。一般地，Fk+1(G)/Fk(G)=F(G/Fk(G)),k=1,2,…。于是得G的一个特征子群列1≤F1(G)=F(G)≤F2(G)≤…≤Fk(G)≤…。因为G是有限群，该特征子群列只能有有限项。若G不可解，则一定存在正整数k,使得Fk(G)=Fk+1(G)

1≤F1(G)=F(G)≤F2(G)≤…≤Fn(G)=G。

此时称n为G的Fitting长或Fitting高，记为nl(G)。

有限群G到G的映射

φ：g→gφ，

称为G的一个算子，如果对于任意x,y∈G。有(xy)φ=xy。G的某些算子组成的集合称为G的一个算子集，算子集常记作Ω。带有算子的群称为算子群，亦称带算群或称Ω群。对任意的a∈Ω,h∈H，有hα∈H，则称H是G的Ω容许子群。

设η可是H到Aut(G)内的一个同态映射，对任意g∈G,规定gh=gη(h)。若A≤G，对∀h∈H,Ah⊆A,则称A是G的H-不变子群，也称A是H-算子群。设X和Y是H-算子群，若存在X到Y的同构ψ使得(xh)ψ=(xψ)h，则称X和Y是H-同构的。令集合

称集合Λ中的极大元素为A的极大H-容许子群，称集合Λ中的极小元素(≠1)为A的极小H-容许子群。

1 预备知识

定义1[2]设G是有限群，若G的自中心化子群都是G的正规子群，则称G是SCN-群。

引理1[2]设G是有限群。则G是SCN-群当且仅当G幂零且幂零类c(G)≤2。

引理2设G是有限群，则G的极大交换子群是自中心化子群。

引理3设G是有限群，则G的非正规极大子群是自中心化子群。

引理4[4]设G是有限群，若G的非正规极大子群的共轭类个数不超过2,则G可解。

引理5[4]设G为有限群，则下述事项等价：

①G恰有一个非正规极大子群的共轭类；

引理6[4]设G为有限群，则下述事项等价：

①G恰有2个非正规极大子群的共轭类；

定义2[10]设G是有限群，H≤G。若存在G的正规子群N,使得G=HN且H∩N≤HG,则称H是G的C-正规子群，其中HG是G的包含在H中的极大正规子群。

引理7[10]设G是群，则：

① 若H在G中正规，则H在G中C-正规；

② 若H在G中C-正规，H≤K≤G,则H在K中C-正规；

引理8[10]设G是有限群，则G可解当且仅当G的极大子群都在G中C-正规。

引理9[10]设G是有限群，则G可解当且仅当G存在可解的C-正规的极大子群。

定义3[11]设G是有限群，若G的子群都在G中C-正规，则称G是CN-群。

引理10[11]设G是有限群，如果G是CN-群，那么G是超可解群，且以下条件等价：

①G是CN-群；

②G可解且C-正规性在G中传递。

引理11[12]设G是有限群，M、N是G的2个不同的极小正规子群，则：

① nl(G)≤max{nl(M),nl(N)};

② 若N≤Φ(G),则nl(G) =nl(G/N)。

引理12[13]设G是有限群，F(G)是G的Fitting子群，若G可解，则CG(F(G))≤F(G),即F(G)是自中心化子群。

引理13[13]设G是有限群，P∈Sylp(G)。若NG(P)=CG(P)，则G是p-幂零群。

引理14[13]有限群G是幂零群当且仅当G的极大子群是正规子群。

引理15[13]设G是有限群，H是G的子群。则H的共轭子群的个数为|G∶NG(H)|。

引理16[13]设G是有限群，H

定义4[14]① 设G是有限群，H≤G,若存在K≤G使得G=HK且H∩K≤HG,称H是G的C-可补子群，或H在G中C-可补。

② 设G是有限群，若G的子群都在G中C-可补，称G是C-可补群。

显然，C-正规子群一定是C-可补子群，CN-群一定是C-可补群。

引理17[14]设G是有限群，Gμ是G的超可解剩余。若Gμ的素数阶子群和4阶循环子群在G中C-可补，则G超可解。

引理18[15]若群G的每个Sylow子群的极大子群是C-正规的，则G为超可解群。

引理19[15]设H为有限群G的极大子群。若H幂零，且H的Sylow 2-群的幂零类不超过2,则G可解。

引理20[15]有限群G是幂零群当且仅当对任一素数p||G|,G都是p-幂零群。

引理21[16]设G是有限非交换p-群。则G的交换极大子群的个数为0,1或1+p。

引理22[17]设G是有限群。若G恰有2个极大子群共轭类，则G只有2种可能：

①G只有2个极大子群，且都正规，此时G为pαqβ阶循环群；

②G有一个极大子群正规，另一类极大子群不正规的pαqβ群。

引理23[18]设G是有限群。若G是非幂零的拟NC-群，则G的Sylow子群都是交换群。

引理24[19]设G是有限群，K是G的交换正规Hall子群，则K在G中有补，且K的补群都共轭。

引理25[20]设G是内交换群，则G有下列互不同构的类型：

1)当G为幂零群时，G必为q-群。

①四元数群：q=2,G=Q8=〈a,b|a4=1,b2=a2,ba=a-1b〉。

②亚循环群：G=Mn,m,q=〈a,b|aqn=bqm=1,ab=a1+qn-1〉，其中n≥2,m≥1。

③非亚循环群：G=Nn,m,q=〈a,b,c|aqn=bqm=cq=1,[a,b]=c,[c,a]=[c,b]=1〉,其中n≥1,m≥1,并且当q=2时，m+n≥3。

2 有限SCCN-群

定义6设G是有限群，若G的自中心化子群都是G的C-正规子群，称G是有限SCCN-群。显然，CN-群和SCN-群是SCCN-群。

定理1设G是SCCN-群，则：

②G是可解群，反之，若有限群G可解，且C-正规性在G中传递，则G是有限SCCN-群；

③ 若Φ(G)≠1,则nl(G)≤2。

证明① 令N≤H≤G且H/N是G/N的自中心化子群，则有

CG(H)/N≤CG/N(H/N)≤H/N,

因此CG(H)≤H，故H是G的自中心化子群。由于G是SCCN-群，故H在G中C-正规。由引理7③知H/N在G/N中C-正规。再根据H的任意性知G/N的自中心化子群都在G/N中C-正规，故G/N是有限SCCN-群。

若N是G的自中心化子群，对任意N≤H≤G，由

CG(H)≤CG(N)≤N≤H,

知H是G的自中心化子群，故H在G中C-正规。由引理7③知H/N在G/N中C-正规，再根据H的任意性知G/N的子群都在G/N中C-正规，即G/N是CN-群。

② 设G是SCCN-群，若G是素数阶群或G=1,则G可解。下面考虑G是非素数阶群，且G≠1。

任取G的极大子群M，则M≠1且M≤NG(M)≤G。由M的极大性知

M=NG(M)或NG(M)=G。

若M=NG(M)，则CG(M)≤NG(M)=M，即M是G的自中心化子群，由G是有限SCCN-群知M在G中C-正规。

由M的任意性，当G是非素数阶群，且G≠1时，G的极大子群都在G中C-正规。由引理8知G可解。

反之，若有限群G可解，且C-正规性在G中传递，由引理10②知G是CN-群，故G是SCCN-群。

③若G有2个不同的极小正规子群M和N,由①知G/M和G/N都是有限SCCN-群。由归纳法知

nl(G/M)≤2,nl(G/N)≤2,

由引理11①知

nl(G)=max{nl(G/M),nl(G/N)}≤2。

若G只有一个极小正规子群N,由于Φ(G)≠1,由归纳法知nl(G/Φ(G))≤2,故由引理11②知nl(G)=nl(G/Φ(G))≤2。证毕。

定理2设G是有限群，若G存在极大子群M，使得M的自中心化子群都在G中C-正规，则G可解。

证明若M=1,此时G为素数阶循环群，当然可解。下设存在M≠1。

因为M的自中心化子群在G中C-正规，由引理7②知M的自中心化子群都在M中C-正规，即M是SCCN-群，由定理1②知M可解。

推论1设G是有限群，若G的所有极大子群的自中心化子群都在G中C-正规，则G可解。

定理3设G是SCCN-群，|G|>1。若F(G)∩G′的素数阶子群和4阶子群在G中C-正规，则G超可解。

推论2设G是SCCN-群，若F(G)∩G′的极小子群和4阶循环子群在G中C-正规，则G超可解。

3 自中心化子群的共轭类个数对有限群结构的影响

为方便起见，记G的极大交换子群的共轭类个数为m(G)。

引理26设G是有限群，则r(G)≥1。

证明由于G本身是G的自中心化子群，故r(G)≥1。证毕。

定理4设G是有限群，则r(G)=1当且仅当G是交换群。

证明设G是交换群，若H是G的自中心化子群，则有

G≤CG(H)≤H,

即H=G,于是得G的自中心化子群只有G本身，即r(G)=1。

反之，任取g∈G,由〈g〉≤CG(g)和CG(CG(g))≤CG(g)，可知CG(g)是G的自中心化子群。又由r(G)=1知G的自中心化子群只有G本身，故CG(g)=G,故g∈Z(G)。由g的任意性知G=Z(G),即G是交换群。证毕。

引理27设G是有限非交换群，则G的极大交换子群的共轭类个数至少为2。

证明假设G的任二极大交换子群共轭，任取H是G的极大交换子群，由引理16得

因此，若G是有限非交换群，G的极大交换子群的共轭类个数至少为2。证毕。

推论3设G是有限群，则m(G)=1当且仅当G是交换群。若G是有限非交换群，则m(G)≥2。

定理5不存在恰含2个自中心化子群共轭类的有限群。

证明设G恰好含2个自中心化子群共轭类。若G是有限交换群，由引理27知r(G)=1。

若G是有限非交换群，由引理27知G的极大交换子群的共轭类个数至少为2,而极大交换子群是自中心化子群，G本身也是G的自中心化子群，故此时G的自中心化子群的共轭类至少为3。

因此，不存在恰含2个自中心化子群共轭类的有限群。证毕。

引理28设G是有限群。若r(G)=m(G) + 1,则G可解。

证明易知G是有限非交换群。设H1,…，Hs是G的所有极大交换子群的共轭类代表，由r(G)=m(G)+1,可知H1,…，Hs恰好是G的所有真自中心化子群的共轭类代表。

若G中的极大子群都正规，则G是幂零群，必为可解群。

若G中存在非正规的极大子群M，由引理3知M是自中心化子群，故M必与某个Hi(1≤i≤s)共轭，这样G中存在交换的极大子群，由引理19知G可解。证毕。

定理6设G是有限群。若r(G)≤5,则G可解。

证明由引理26和定理5可知，只需考虑r(G)=1,3,4,5的情形。

① 当r(G)=1时，由引理27知G是交换群，故G可解。

② 当r(G)=3时，由引理27知此时G的极大交换子群的共轭类个数为2,故由引理28知G可解。

③ 当r(G)=4时，G的极大交换子群的共轭类个数为2或3。

若G的极大交换子群的共轭类个数为3,则由引理28知G可解。

若G的极大交换子群的共轭类个数为2,不妨设H1、H2为G的极大交换子群的共轭类代表，则H1、H2也是G的自中心化子群的共轭类代表，若H1、H2中的某一个为极大子群，则G已可解。若H1、H2都不是极大子群，考虑G的非正规极大子群，由于G的非正规极大子群是自中心化子群，且r(G)=4,故此时G的非正规极大子群的共轭类个数≤1,由引理4知G可解。

(4)当r(G)=5时，G的极大交换子群的共轭类个数为2、3或4。

若G的极大交换子群的共轭类个数为4,则由引理28知G可解。

若G的极大交换子群的共轭类个数为3,不妨设H1、H2、H3为G的极大交换子群的共轭类代表，则H1、H2、H3也是G的自中心化子群的共轭类代表，若H1、H2、H3中的某一个为极大子群，则G已可解；若H1、H2、H3都不为极大子群，考虑G的非正规极大子群，则此时G的非正规极大子群的共轭类个数≤1,由引理4知G可解。

若G的极大交换子群的共轭类个数为2,不妨设H1、H2为G的极大交换子群的共轭类代表，则H1、H2也是G的自中心化子群的共轭类代表，若H1、H2中的某一个为极大子群，则G已可解；若H1、H2都不为极大子群，考虑G的非正规极大子群，则此时G的非正规极大子群的共轭类个数≤2,由引理4知G可解。证毕。

定理7不存在恰含3个自中心化子群共轭类的非交换p-群。

证明设G是有限群，且r(G)=3,则G是非交换群。设H1、H2是G的真自中心化子群的共轭类代表，则H1、H2恰是G的极大交换子群的共轭类代表。假如G是有限非交换群p-群，则下述事实成立：

①G的交换极大子群恰有2个共轭类，且H1、H2是G的交换的极大子群的共轭类代表。

若H1不是G的极大子群，则存在G的极大子群M满足H1≤M，由

CG(M)≤CG(H1)≤H1≤M，

知M是G的自中心化子群，由r(G)=3知M与H2共轭，这与H1是极大交换子群矛盾，故H1是极大子群。同理可得H2是极大子群。若G中存在交换极大子群M0,且M0不与H1共轭，也不与H2共轭，则M0属于G的另一个自中心化子群的共轭类，这与r(G)=3矛盾。

②G的非交换极大子群是正规子群。

设M1是G的非交换极大子群，若M1是非正规的，则M1是G的自中心化子群，由r(G)=3知M1与H1共轭，或与H2共轭，2种情况都与M1的非交换性矛盾。

③G中存在一个正规的交换极大子群，另一类交换极大子群非正规。

因为G是有限非交换群p-群，故G的交换极大子群的个数为0、1或p+1。由①知G的交换极大子群的个数为p+1。由于Hi(i=1,2)的共轭子群的个数为|G∶NG(Hi)|,是|G|的因子，又|G∶NG(H1)|+|G∶NG(H2)|=p+1,因此|G∶NG(H1)|和|G∶NG(H2)|只能一个为1,一个为p。

以上说明G的非正规的极大子群都共轭，故G的结构为引理5的②和③，显然②和③都不是p-群，矛盾。证毕。

定理8设G是有限幂零群，且r(G)=3,则G的幂零类c(G)=2。

证明由r(G)=3知G是非交换群，且G恰有2个极大交换子群的共轭类。设H1、H2为G的真自中心化子群的共轭类代表，则H1、H2也是G的2个极大交换子群共轭类代表。由G幂零得H1

证明当r(G)=3时，设H1、H2为G的自中心化子群的共轭类代表，由引理16知H1、H2也是G的2个极大交换子群共轭类代表，任取G的交换子群A。

若A是极大交换子群，不妨A=H1,有H1=A=CG(A)≤NG(A),又NG(A)是G的自中心化子群。若NG(A)与H2共轭，则与H1是极大交换子群矛盾。若NG(A)=G,即AG。若NG(A)与H1共轭，则有NG(A)=CG(A)。

若A是非极大交换子群，不妨A

定理10设G是有限群，且r(G)=3。则G的结构是下列情况之一：

①G为q-基本群，并且|G|=pαqβ,p、q为素数，α、β为正整数，G恰有2个极大子群共轭类，其中一个极大子群正规，另一个极大子群非正规。

证明若G的极大子群都是交换群，此时G为内交换群。若G是幂零群，由引理25知G是q-群，但由引理27得不存在自中心化子群共轭类个数恰为3的非交换p-群，因此G是非幂零群，故G是q-基本群。又因G为内交换群，从而G的极大交换子群与极大子群等价，即G恰有2个极大子群共轭类。由引理22及引理27的证明过程知G有一个极大子群正规，另一类极大子群不正规的Pαqβ群，即定理10①。

若G中存在非交换的极大子群，则非交换的极大子群都是正规子群(假如存在非正规的非交换极大子群M，则M是G的自中心化子群，而G中至少含有2个极大交换子群共轭类，这样与r(G)=3矛盾)。而非正规的极大子群是自中心化子群，由r(G)=3知G的非正规极大子群的共轭类个数为1或2。故由引理5和引理6可得定理10结论中的②～⑤结构。证毕。