外激和参激作用下的三角翼飞行器滚转运动的随机响应

焦萌倩,彭如月,黄文韬,蒋贵荣*

(1.桂林电子科技大学 数学与计算科学学院，广西 桂林 541004；2.广西师范大学 数学与统计学院，广西 桂林 541006)

随着科学技术的飞速发展，飞行器需要完成各种各样的高难度动作，机翼摇滚是常见的横向不稳定现象，因而研究飞行器滚转运动已经成为当下科技发展的需要。飞行器在实际飞行中遇到外部环境以及内在动因所带来的各种随机噪声是不可忽视的。Konstadinopoulos等[1]利用非定常涡格法分析了低速条件下细长三角翼摇晃的现象，这种方法便于计算，但其前提假定导致应用受到很大的限制和约束；Elzebda等[2]比较了细长三角翼的3种分析模型，发现仅包含二次项的原始模型不能预测滚转发散，并在修正模型基础上得到运动方程解的渐近逼近；刘伟等[3]对静稳定下的细长三角翼运动出现Hopf分叉的临界条件进行了分析，并利用耦合三维非定常Navier-Stokes方程与Euler刚体运动方程进行数值模证实了其理论分析。

随机动力学一直都是研究热点[4]。Zhu等[5]利用广义调和函数提出了针对单自由度强非线性振子的随机平均法，并对Duffing-vanderPol振荡器在宽带随机参激和外激共同作用下的响应进行了分析,还利用该方法分析了带有2种参激的Duffing-vanderPol振荡器系统的平稳概率密度和Hopf分岔；黄志龙等[6]利用广义谐和函数的随机平均法及Galerkin法研究了受高斯白噪声激励带有时滞反馈控制的单自由度强非线性系统，通过将其转化为不具时滞的系统再利用随机平均法求得响应的近似瞬态概率密度；Miles[7]提出了一种近似方法，用于估算Duffing振子在用高斯白噪声驱动时的响应功率谱密度并发现随着随机激发的幅度增加，响应谱中的谐振响应峰值趋于变宽；黄开娇等[8]研究了含Lévy噪声的随机捕食-被捕食系统，利用李雅普诺夫函数等得到系统存在唯一全局正解；仲淑娟等[9]利用李雅普诺夫函数和多尺度法，针对谐和与随机噪声下的非线性系统的响应进行了研究。

近几年，很多学者也开始注重随机理论在实际应用中的研究[10-12]。谭建国等[13]讨论了模型在随机参数激励下的稳定性与可靠性，在原有二元机翼模型的基础上加入随机因素，研究了噪声强度对系统的可靠性的影响，但其仅考虑了随机气流速度的影响，涉及到的随机因素还不够全面；葛根等[14]先运用Galerkin变分法将矩形薄板的受面内随机激励的振动模型简化为常微分非线性动力学方程，并利用拟不可积Hamilton随机平均及伊藤方程微分法则等理论将方程简化为一维随机微分方程进行研究，通过稳态概率密度函数的形状分析了系统的随机分岔现象；覃英华等[15]采用数值模拟的方法分析了噪声对电力网络稳定性的影响，随机噪声使得电力网络最终达到崩溃，因此在实际应用中噪声不容忽视。

随机系统的平稳概率密度的计算难度很大，一般情况下很难得到精确表达式。在已有文献中，大部分学者在研究三角翼滚转运动时考虑参激或者外激，为了理论分析系统的随机响应考虑特殊的微分方程。本文在更为复杂的微分方程的基础上，同时引入外激和速度参激，利用耗散能量平衡法、幅值包线随机平均法、能量包线随机平均法求得三角翼滚转运动系统近似平稳概率密度的解析解，并进行数值模拟。

本文内容安排如下：第1章建立随机三角翼滚转运动模型；第2章运用耗散能量平衡法，通过求系统的概率势直接得到近似概率密度；第3章通过进行vanderPol变换，运用幅值包线随机平均法求得系统近似概率密度；第4章运用能量包线随机平均法求得近似解；第5章给出数值模拟和结论。

1 系统模型

考虑单自由度滚转运动方程[16]

(1)

(2)

将式(2)代入式(1)可得

(3)

式中ω2=D-ca1，α=-ca2，β=-ca3，γ=-ca4，η=-ca5。

在模型(3)的基础上考虑随机因素，加入噪声分别为速度乘性噪声和加性噪声。当噪声均为高斯白噪声时，模型为

(4)

式中W1(t)和W2(t)是相互独立高斯白噪声，其功率谱密度与自相关函数分别为

ΦWiWi(ω0)=Kii,RWiWi(τ)=2πKiiδ(τ),i=1,2,

式中：δ(τ)为狄拉克函数；Kii为高斯白噪声的强度。

2 耗散能量平衡法

非线性系统只有在特定条件下才可以求得其精确解，但实际很难满足限定条件，因此，人们发展了一系列求解非线性系统近似解的方法。耗散能量平衡法是等效非线性系统法的一种，其可以直接找出系统的概率势，减少误差的产生。为应用耗散能量平衡法，引入状态变量

将式(4)写成单自由度非线性随机系统标准形式

(5)

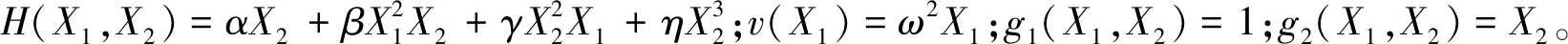
按Wong-Zakai修正项识别附加恢复力u*(X1)与附加阻尼力h*(X1,X2)的关系如下

由此可得

u*(X1)=0,h*(X1,X2)=πK22X2。

(6)

系统(4)恢复力是线性的，可做如下变换

(7)

由式(5)、(6)及变换(7)可得其概率势函数导数为

故系统平稳概率密度为

p(x1,x2)=Cexp[-ψ(λ)]=

(8)

3 幅值包线随机平均法

幅值能量平衡法主要应用于恢复力是线性的系统，该方法主要任务是进行vanderPol变换，将系统变为受小非线性阻尼与弱激励扰动的拟线性振子的幅值与相位，并对其在拟周期上进行时间平均。对系统(4)进行如下vanderPol变换[17]

(9)

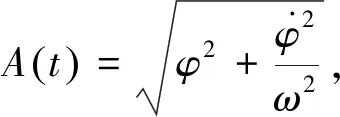
(10)

(11)

将A(t)看作X1(t)，φ(t)看作X2(t)，利用式(10)、(11)可得下列标准形式：

(12)

(13)

(14)

(15)

(16)

A(t)和φ(t)构成一个马尔可夫扩散过程，且系统以2π/ω为拟周期运动，故可对式(13)～(16)在一个拟周期上做如下时间平均

并运用伊藤微分规则得幅值的伊藤方程。平均后幅值A(t)的方程不含相位φ(t)，故得到幅值的光滑伊藤方程为

dA=m(A)dt+σ(A)dB(t),

(17)

式中：

(18)

(19)

对应的FPK方程为

为求解该FPK方程，需先求解A(t)的与时间无关的平稳概率密度p(A)。易知该平稳概率密度满足下列简化的FPK方程

(20)

对式(20)积分得

(21)

由式(21)可知概率G(A)在任何处均为常数。为确保平稳概率密度p(A)存在，对有限或无穷边界最常见的情形是概率流为零，故可从式(21)得简化的解

(22)

(23)

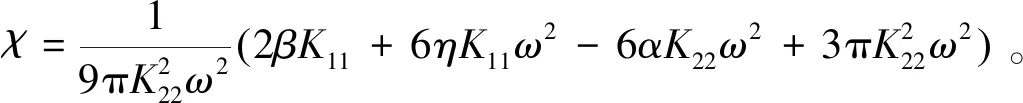
4 能量包线随机平均法

能量包线随机平均也称为拟保守平均，首先考虑系统的无阻尼自由振动方程为

(24)

势能与总能量分别为

(25)

周期为

(26)

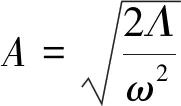
(27)

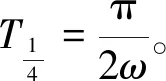
由于激励是高斯白噪声,可得系统漂移系数和扩散系数

(28)

(29)

时间平均按式(30)进行

(30)

于是，支配能量Λ(t)的伊藤方程为

由此可得Λ(t)的平稳概率

(31)

式中C2为积分常数，且

5 数值模拟和结论

在系统(4)中，取ω=0.4,α=0.6,β=1.2,γ=0.8,η=0.49,K11=0.4,K22=0.3。系统(4)过初始点(1,2)的一个样本解的相图和时间序列如图1所示。

图1 系统(4)在ω=0.4,α=0.6,β=1.2,γ=0.8,η=0.49,K11=0.4,K22=0.3下的一个样本解的相图和时间序列Fig.1 Phase diagram and time sequence of a sample solution of system (4)with ω=0.4,α=0.6,β=1.2,γ=0.8,η=0.49,K11=0.4,K22=0.3

利用耗散能量平衡法、幅值包线随机平均法、能量包线随机平均法求得系统(4)的近似平稳概率密度表达式分别为式(8)、(23)和(31)，分别如图2(a)、(b)、(c)所示。

图2 系统(4)在ω=0.4,α=0.6,β=1.2,γ=0.8,η=0.49,K11=0.4,K22=0.3下的平稳概率密度Fig.2 Approximate probability density of system (4) withω=0.4,α=0.6,β=1.2,γ=0.8,η=0.49,K11=0.4,K22=0.3

为比较每个方法得到的平稳概率密度的精确性，现在计算E(φ2)。根据近似平稳概率密度(8)、(23) 和(31)计算的E(φ2)的图象在图3中分别用M-1、M-2、M-3表示。M-4是对系统(4)的φ2的蒙特卡罗模拟结果，其中样本容量为1万个。从图3(a)可以看出，耗散能量平衡法得到的平稳概率密度误差最大；图3(b)可以看出，能量包线随机平均法得到的平稳概率密度最精确。

图3 系统(4)在ω=0.4,α=0.6,β=1.2,γ=0.8,η=0.49,K22=0.3和K11∈(0.3,0.6)下的E(φ2)Fig.3 E(φ2) of system (4) with K11∈(0.3,0.6) and ω=0.4,α=0.6,β=1.2,γ=0.8,η=0.49,K22=0.3

本文在更为复杂的描述三角翼滚转运动的微分方程的基础上，同时引入外激和速度参激，利用耗散能量平衡法、幅值包线随机平均法、能量包线随机平均法求得了三角翼滚转运动系统近似平稳概率密度的解析解，通过数值结果，能量包线随机平均法得到的平稳概率密度最精确。所得结果可以为三角翼飞行器滚转运动的监控策略的制定等提供理论依据。