横流转捩模型参数不确定度量化分析与应用研究

向星皓，张毅锋，陈坚强,2，袁先旭,2，陈树生

(1. 中国空气动力研究与发展中心空气动力学国家重点实验室，绵阳 621000；2. 中国空气动力研究与发展中心计算空气动力研究所， 绵阳 621000；3. 西北工业大学航空学院，西安 710072)

0 引 言

边界层转捩通常是指边界层流动由层流状态发展为湍流状态的过程，是一个多因素耦合影响、包含复杂转捩机理的物理现象[1]。真实飞行器的三维边界层转捩往往由横流转捩主导[2]。作为转捩预测手段之一的转捩模型在构造过程中涉及到较多模型参数，大部分参数是通过特定条件下的风洞实验和理论分析来确定的，其适用范围有限，在实际应用中往往需要针对不同流动类型进行参数调整。

由于实验数据获取困难以及缺乏对转捩机理的深入理解，在转捩模型的构造过程中存在一定的认知不确定性。虽然该不确定性会随着人们对物理模型了解的深入和实验数据的丰富而逐步减小，但是目前仍会导致模型参数不确定性。这主要体现在给定的模型参数未必最优，针对具体转捩类型与流场特性，需要对参数进行标定与修正。

模型参数的标定通常是确定性的，给出了参数具体取值或取值范围。如文献[3]用特定工况的理论分析和风洞实验，结合建模中的部分假设直接确定模型参数取值。也有采用类似试错法进行参数调整，如Lien等[4]在建模以后对参数进行变参数调整优化，在特定算例中对模型参数进行试错调整，实现一个较小范围的参数最优。

不确定度量化分析相比以往确定性的参数标定，能够提供多参数对转捩起始位置耦合作用的定量影响[5]、能够定量给出计算结果不确定度范围以及所需样本量小[6]等诸多优势，对于参数标定工作以及模型参数效能分析具有重要的指导意义。不确定度分析具有非侵入式以及对随机输入变量具有指数收敛性的特点[6]，能够提供输入条件对转捩起始位置的定量影响[5]。

由于认知不确定性造成的转捩模型参数不确定性因素普遍存在，不确定度量化分析就显得尤为必要。张涵信院士等[7]指出，CFD方法的不确定度或可靠性一直以来都是CFD中需要特别关心的问题。不确定度量化分析对于转捩模型参数研究具有重要意义，能够提供参数敏感性以及不确定度的定量结论，进而对参数效能研究以及模型参数的筛选调试提供具体有效的指导。在此基础上，不确定度量化分析方法可以甄别对计算结果影响大的关键因素，为转捩模型的改进指明方向。

在转捩/湍流模型的不确定度量化分析方面，目前关于模型不确定度研究主要集中在湍流模型方面，对于转捩模型的不确定度研究则相对有限。Pecnik等[5]对由于自由来流不确定性与可压缩修正所导致的转捩模型不确定度进行了分析，分析发现上述因素对转捩起始位置与气动热分布的不确定度造成显著影响。Zhao等[8]对转捩模型在高超声速平板和尖锥中的不确定度和参数敏感性开展研究，采用非嵌入式多项式混沌(Non-intrusive polgnomial chaos,NIPC)方法对γ-Reθt和k-ω-γ转捩模型进行了基于来流不确定性的不确定度量化分析。

传统不确定度分析方法如工程应用较为普遍的蒙特-卡洛(Monte-Carlo)方法，在对计算流体力学气动力、热不确定度分析时，样本需求量大，计算资源消耗大[9]。相对于蒙特-卡洛方法而言，非嵌入式多项式混沌(NIPC)方法不需要修改求解器，具有计算量小、收敛快的特点，在复杂模型、系统的不确定度量化分析中得到广泛应用[10]。

本文首先基于课题组Chant 2.0计算平台[11]实现了当地化横流转捩模型[12-13]，然后采用非嵌入式多项式混沌方法对NLF(2)- 0415后掠翼和S-K低速平板进行了模型参数不确定度量化分析和参数敏感性分析，得到了当地化的横流转捩模型参数不确定性的定量分析结果。以分析结果为指导对横流转捩模型进行了重新标定与参数修正，最后将修正的转捩模型在NLF(2)- 0415后掠翼、6:1标准椭球体和DLR-F4翼身组合体算例中进行了验证。计算结果表明，重新标定的模型对于亚声速、跨声速情况下的三维边界层转捩具有较好适用性。

1 计算方法

1.1 控制方程

本文采用有限体积法对雷诺平均Navier-Stokes(RANS)方程进行求解，无黏通量计算格式为AUSMPW+，无黏项离散格式为二阶精度NND格式，黏性项离散格式为二阶中心差分格式，时间推进采用LU-SGS方法，湍流模型采用k-ωSST模型，采用MPI技术进行大规模并行计算。

1.2 横流转捩模型的不确定度输入参数选取

本文在Chant 2.0计算平台实现了文献[12-13]提出的当地化横流转捩预测模型。由于计算平台差异，模型参数需要重新标定。对模型开展了转捩相关量不确定度量化分析和参数研究，以指导参数标定工作。横流模型基于γ-Reθt转捩模型进行拓展，横流效应是通过在原始模型的Reθt输运方程中增加横流源项来实现的。

(1)

(2)

(3)

cCF=0.6

(4)

在横流源项DSCF中有两个模型参数作为横流源项的系数而存在，分别是cCF和cθt。上述参数大小会直接影响输运方程中的横流源项大小，影响模型预测的横流转捩起始位置，是横流转捩不确定性研究的重点关注参数。

物面粗糙度作为物体表面固有属性参数，在大多数风洞实验、飞行试验以及CFD横流模型预测中，这一重要参数往往是缺省的，或者测量存在一定的误差。在本文所用的横流转捩模型中，表面粗糙度h是定常横流转捩判据ReSCF的重要参数之一，见式(5)。本文将粗糙度h作为输入参数之一进行不确定度和参数敏感性分析。

319.51+f(+ΔHCF)-f(-ΔHCF)

(5)

综上所述，本文选取模型参数cCF和cθt以及表面粗糙度h进行不确定度与参数敏感性分析，对模型参数进行筛选与横流标定。横流转捩模型的其余参数则与γ-Reθt模型一致，见文献[12]。

1.3 不确定度分析方法

传统的CFD数值模拟具有确定性，即针对一个确定的问题通过一组确定性的输入从而得到一个确定性的计算结果[10]。对于转捩模型而言，由于转捩机理的高度复杂性和在风洞实验和飞行试验中测量的困难，以及对模型认知存在的局限，导致构建的转捩模型的参数也存在较大不确定性[11]。因此有必要针对转捩模型参数所导致的转捩起始位置和转捩特征量的预测不确定性进行不确定度量化分析。

本文采用非嵌入式多项式混沌方法进行不确定度量化分析。在CFD转捩预测模型不确定度分析中，以壁面摩擦力系数Cf、转捩起始位置等重要参数作为随机输出变量，表示为：

(6)

式中:α*是CFD直接计算结果，αj(x)是计算结果的确定部分耦合系数，ψj(ξ)是计算结果的随机部分。ξ=(ξ1,…,ξn)是n维随机变量，而随机部分ψj(ξ)是以随机变量ξ为自变量的随机函数，为ξ的正交多项式。

随机函数ψj(ξ)根据随机变量的ξ分布，即本文输入的转捩模型参数的分布类型不同而有所区别，对应选取不同形式的正交多项式。若模型参数满足均匀分布时，正交多项式选择Legendre正交多项式；若模型参数满足正态分布时，正交多项式选取Hermite正交多项式[9]。

对多项式采取p阶截断，设随机参数的维数为n，则混沌多项式(PCE)项数可以表示为：

(7)

本文选取随机响应面法求解混沌多项式系数，开展不确定度分析。参数样本量的设置，参考文献[14]选用PCE系数两倍的过采样方法。根据Schaefer等[15]的比较结果，采用精度和收敛性均表现较好的拉丁超立方(LHD)抽样方法，对模型参数进行抽样选取。

选取了Nt个随机样本点后，每一个样本点对应一个确定的CFD计算结果，由式(6)可得[9]：

(8)

采用最小二次回归对PCE系数αi进行求解[9]，平均值μ和方差D按如下计算：

μ=α0(x)

(9)

(10)

每一个输入参数变量i对输出变量不确定度贡献的相对大小是通过敏感性指数来表征的。Sobol指数(STi)作为敏感性指数定义为部分方差与总方差的比值[16]：

(11)

其中部分方差与总方差分别为：

(12)

(13)

针对输入参数i的Sobol指数(STi)则定义为包含变量i的所有部分Sobol指数之和：

(14)

2 不确定度与参数敏感性分析

本文选取S-K低速平板和NFL(2)- 0415后掠翼两个算例进行不确定度量化和参数敏感性分析。第一个算例的边界层转捩由T-S波主导，第二个算例是由横流不稳定性主导。通过上述两个算例的NIPC分析，能够得到模型参数在不同转捩类型中的效能，从而进行有针对性的参数修正工作。

选取三个模型参数作为输入，选取两个物理量作为输出响应，进行不确定度量化分析。两个输出响应为：转捩起始位置xtr和壁面摩擦力系数Cf。三个输入参数及依据为：1)动量厚度雷诺数输运方程中横流破坏项系数参数cCF,该参数作为横流耗散项DSCF系数(见式(2))，对模型的横流转捩预测影响较大；2)表面粗糙度h，该参数构成横流转捩判据ReSCF迭代式，必然对横流转捩产生影响；3)γ-Reθt转捩模型和横流模块DSCF项共有的系数参数cθt。

上述三个参数对横流转捩存在重要影响是显而易见的，本文目的主要在于采用NIPC方法对参数影响进行定量分析，得出不确定度和参数敏感性的定量结论，进一步指导参数标定工作。

输入参数的不确定度范围设置如下：横流参数cCF基准值根据文献[13]设置为原始值0.6，正负偏差百分比根据模型标定经验[17]设置为±66.66%，对应参数变化范围[0.2，1.0]；参数cθt基准值设置为0.03[12]，不确定度正负偏差百分比为±20%，对应参数变化范围[0.024，0.036]；表面粗糙度h根据机加工精度覆盖从不可辨加工痕迹的超级加工光泽面至粗糙漆面[13,18-19]，粗糙度变化范围为[0.5，10]，单位μm。

混沌多项式(PCE)采用2阶截断，根据式(7)采用过采样方法，选取样本数为20，采用拉丁超立方进行抽样，选择转捩起始位置和壁面摩阻系数作为输出响应。在95%的置信区间下，转捩起始位置与摩阻系数Cf输出响应的不确定度为UQ%=100×1.96σR/μR。

2.1 S-K低速平板算例

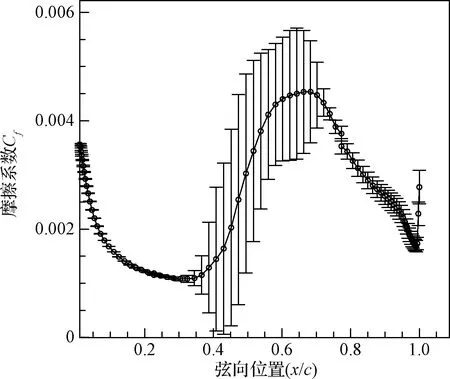
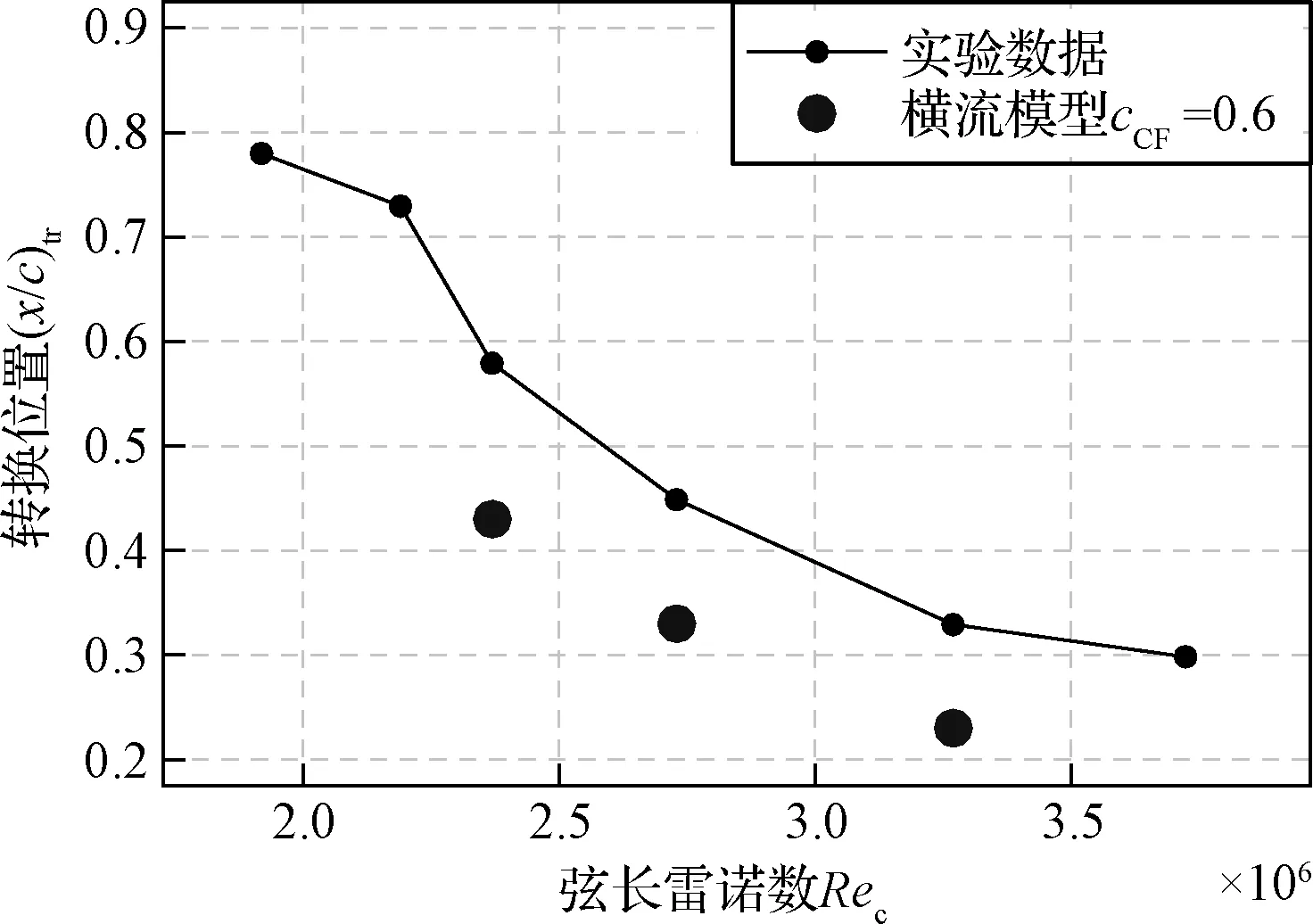
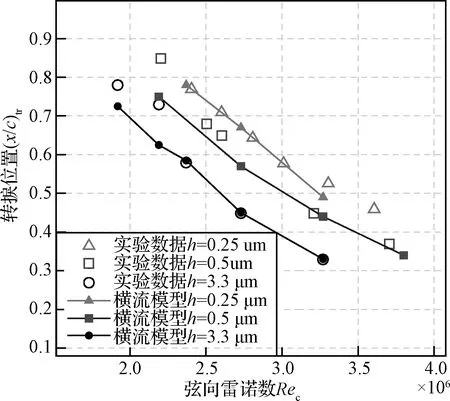
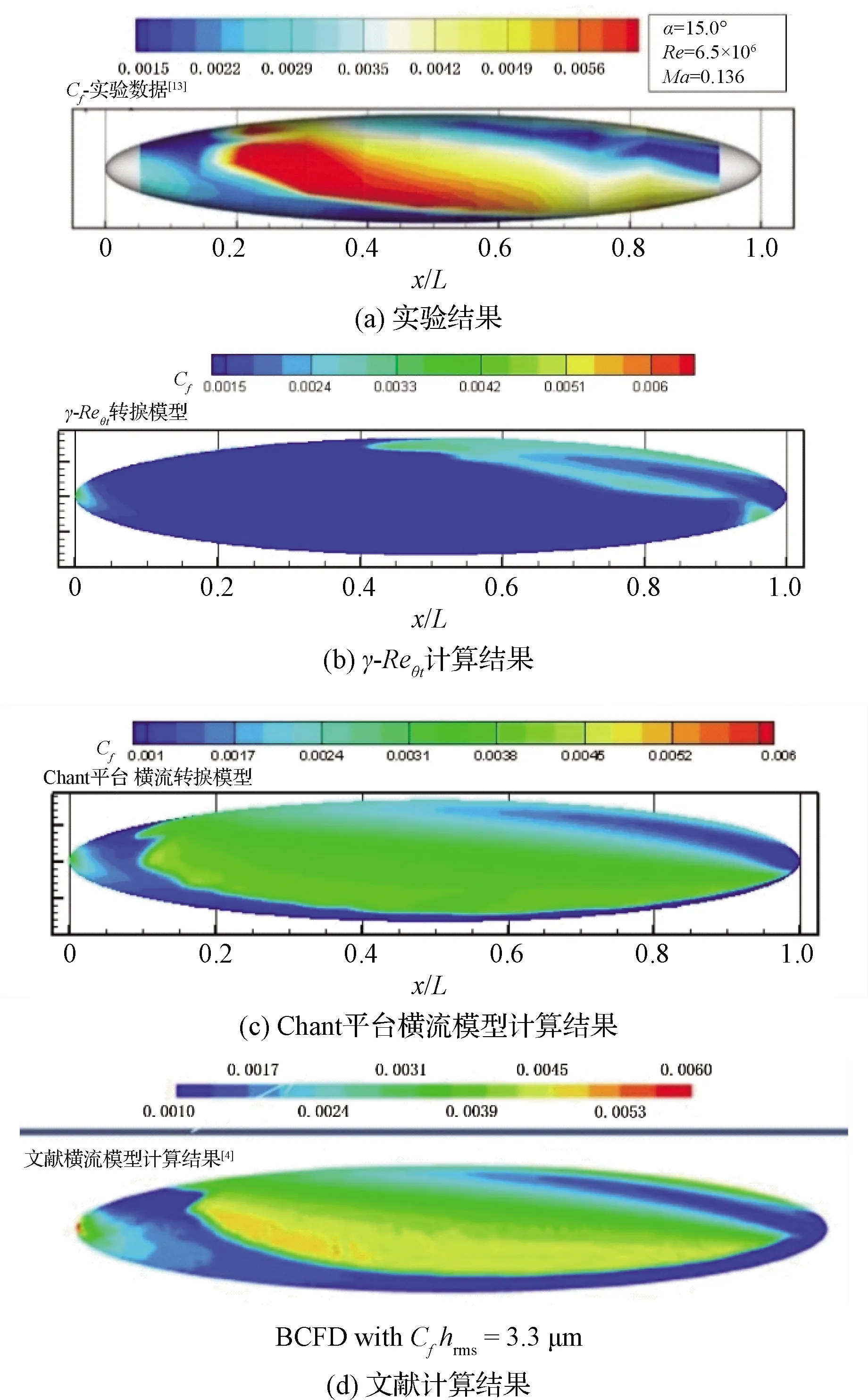
S-K低速平板来流状态为Ma=0.147,Re=3.34×106/m,来流湍流度Tu∞=0.18%。以摩阻系数Cf为输出响应进行了基于三参数的不确定度与参数敏感性分析，通过不同站位上三个输入参数对应的敏感性指数比较，可以观察输入参数在不同流动过程的影响程度。由图1可知，在转捩区(0.8

图1 低速平板算例壁面Cf不确定度与参数敏感指数Fig.1 UQ% & sobol index of Cf in S-K flat plate

与摩阻系数类似，以转捩起始位置为输出响应也可以给出三个参数的敏感性指数，计算结果见表1，模型参数cθt的敏感性指数大约是参数cCF与物面粗糙度h的敏感性指数的2倍，与图1的结果一致。在相对幅值变化相同的条件下，参数cθt所引起的转捩起始位置xtr的变化同样更为显著。

表1 低速平板算例转捩起始位置的三参数敏感性指数Table 1 Sobol index in S-K flat plate case

该算例说明，cθt是影响T-S不稳定性主导转捩计算的主要参数，调整模型参数cθt获得的敏感性高于其他两个参数，在对流向转捩进行标定时，应主要考虑参数cθt。

2.2 NFL(2)- 0415后掠翼算例

2.2.1模型参数不确定度量化

NFL(2)- 0415后掠翼上表面转捩过程由横流不稳定性主导，选取上壁面摩阻系数Cf和转捩起始位置xtr作为输出响应进行分析。不确定度分析的NFL(2)- 0415后掠翼算例计算状态为攻角-4°,Ma=0.2，Re=3.27×106/m，来流湍流度Tu∞=0.09%，边界层远场湍流度自由衰减至Tu≤0.02%。

图2是所有拉丁超立方抽样样本的上表面摩阻系数Cf分布图，并给出NIPC均值进行对照。在20个样本曲线中，转捩起始位置在x=0.43附近有5条Cf曲线基本重合，对应样本编号为7,12,13,19,20(见表2)。它们中的参数cCF与参数h有此消彼长的关系，说明两参数对横流转捩的影响作用近似。

图2 采样样本的上壁面Cf分布图Fig.2 Cf distribution of all samples

表2则是采用拉丁超立方抽样归一化参数样本(参数样本：最大值→1，最小值→-1)。该不确定度分析手段具有“样本量小、信息丰富”的特点。与常规变参分析进行对比，若采用常规单参数调试的方法，假设每个参数在指定范围内进行六个均匀采样，则在样本量相当的情况下，传统方法只能得到单参数调试结果，无法得到参数耦合变化下的不确定度与参数敏感性分析结果(见图3、图4)。

表2 拉丁超立方抽样输入参数及转捩起始位置Table 2 LHD sampling and transition location

图3是基于参数抽样结果的壁面摩阻系数均值及误差带分布。其意义在于仅采用了少量样本，即提供了变参数横流转捩模型输出量的整个空间分布及其变化范围。如采用传统变参分析，其参数样本量与计算量将远大于此。

由图3可知，在x<0.4的层流区和x>0.7以后的充分发展湍流区，误差带范围明显低于在0.4

图3 NIPC方法壁面摩擦系数均值及误差带分布Fig.3 Surface Cf distribution with NIPC method

图4 后掠翼算例Cf不确定度与参数敏感指数分布Fig.4 UQ & Sobol Index of Cf on back-swept wing

将上述参数采样和对应计算结果作为输入与输出，采用NIPC方法进行不确定度分析。图4为摩阻Cf作为输出响应的不确定度与参数敏感性指数沿弦向分布，敏感性在第2.2.2节进行分析。不确定度的分布与图3误差带区间分布具有一致性，在x<0.4与x>0.7的区间近似为0，在转捩区间呈现出“两端小、中间大”的分布规律。转捩区域中x/c=0.43时Cf不确定度达到最大，大小约为189%。

2.2.2模型参数敏感性分析

对转捩起始位置xtr和壁面摩擦系数Cf分布分别进行了参数敏感性的点分析和线分析。二者反映不同物理量对参数变化的敏感程度，转捩起始位置三参数点分析的敏感性指数(见表3)，不能通过壁面摩擦系数敏感性指数分布(见图4)直接得到。

以转捩起始位置xtr为输出响应，进行参数敏感性的点分析。表3给出了经不确定度点分析的转捩起始位置敏感性指数，三参数的Sobol指数分别为0.56153，0.43323，0.12676，该指数表征参数敏感程度，参数cCF与h的敏感性指数约为参数cθt敏感性指数的3～4倍，其对横流转捩起始位置的影响要远大于参数cθt。

表3 后掠翼转捩起始位置的三参数敏感性指数Table 3 Sobol index in back-swept wing case

以摩阻Cf为输出响应，进行参数敏感性的线分析见图4。从图4可以看出，对转捩区间Cf分布影响较大的参数是cCF与表面粗糙度h，其敏感性指数在转捩区域内(0.40.8的区间，cθt的敏感性指数趋于0，即cθt几乎不影响转捩前的层流区域和转捩后的湍流区域的Cf分布。但cCF,h与cθt的敏感性指数规律不同，它们仅在x<0.4的层流区域近似为0，在x>0.8转捩完成以后的湍流区域，cCF敏感性指数约为0.3，h的敏感性指数约为0.4。说明横流参数cCF与表面粗糙度h不仅影响转捩起始位置，还会对转捩之后的Cf分布造成一定影响。与该观点相互印证的是图3中误差带分析结果，x∈[0.8,1]区域内误差带不为零，该区域内的不确定度大约在4%～8%的范围内。调整参数cCF和h，能使转捩起始位置相对于流向转捩提前发生，模拟横流转捩效果。

2.3 不确定度与参数敏感性分析小结

相比常规变参分析方法，不确定度量化分析方法具有如下显著优势：

1) 不确定度量化分析能够给出研究者所关心的输出物理量的不确定度定量范围，具有重要的工程指导意义。

2) 不确定度量化分析所给出的参数敏感性指数，可以直接量化参数在特定空间位置对特定物理量的影响大小，而常规变参分析只能给出影响大小的宏观定性排序。前者对于参数筛选与标定工作更具指导意义。

3) 基于NIPC的不确定度分析，采用拉丁超立方抽样需要的样本量小，得到的信息丰富，效费比高，能够综合考虑多参数耦合变化时的参数作用效应。常规变参数分析不具备上述特点。

三输入参数以不同的作用方式都对转捩模拟结果有影响，不同的转捩方式需采用不同的参数进行标定：

1) 参数cθt对流向转捩相关量的不确定度影响较大，敏感性较高，且对于横流转捩影响较小。流向转捩模型的标定应主要针对参数cθt开展。

2) 参数cCF对横流转捩相关量的不确定度影响较大，敏感性较高，且cCF对于流向转捩影响较小，对横流模型的标定应主要针对参数cCF开展。

3) 表面粗糙度h是反映模型加工表面光洁程度的固有参数，对横流转捩位置xtr以及Cf分布均存在显著影响。不同风洞实验、飞行试验的模型表面由于加工精度不同，粗糙度差别较大，需要对其精确测量。

3 横流转捩模型参数标定与校验

本文主要研究横流转捩模型参数，根据不确定度和参数敏感性分析结果，对模型参数进行筛选，给出参数cCF的标定和校验结果。

3.1 横流模型参数标定

针对不同计算平台的模型参数标定的广泛需求，以不确定度和参数敏感性分析结果为指导，进行模型参数筛选和标定。

NFL(2)- 0415后掠翼算例来流状态为Ma=0.2,Re=1.9～3.3×106/m (1.93×106, 2.19×106, 2.40×106, 2.73×106, 3.27×106)。在Chant 2.0计算平台上采用基准参数的横流模型，由于计算平台差异，采用原始基准参数的模型预测的NFL- 0415(2)后掠翼转捩起始位置与实验结果偏差较大，如图5所示。在雷诺数为3.27×106算例中转捩起始位置偏差大约在30%以上。根据现有的NFL- 0415后掠翼转捩实验数据[19]，采用改变模型参数值的方法调整横流转捩起始位置，对横流转捩模型进行重新标定。表面粗糙度设置为实验测量结果[13,19](h=3.3 μm)。

图5 基准参数模型预测转捩起始位置与实验对比Fig.5 Transition location of modeling and experiment

由第2节不确定度与参数敏感性分析结果可知，在横流不稳定性主导的转捩中，模型参数cCF和cθt均影响转捩位置，但cCF的参数敏感性指数更高(见表1和图4)。同时cCF仅是动量厚度输运方程横流源项系数，该系数的调整与横流转捩位置变化具有单调一致性。因此选取参数cCF进行横流标定。

虽然常规变参分析可以选取横流耗散项DSCF系数cCF进行直接标定，但参数选取及变参数调试缺乏定量的误差带和敏感性数据支持，经验性较大。

图6 变参数的后掠翼的计算和实验结果[19]Fig.6 Experiment & modeling results with varying parameter values[19]

就参数cCF对输运方程的影响进行定性分析：该系数越小，Reθt输运方程横流破坏项占比越低，由间歇因子输运方程启动项对Reθt的单调性，减小该系数使转捩起始位置后移。极限情况下cCF参数为0，横流模型恢复至原始γ-Reθt转捩模型。

根据上述分析以及图3的采样样本结果，以表1样本17, 3, 8为参考，设置参数cCF的标定范围为[0，0.6]，选取cCF=0, 0.05, 0.1, 0.15, 0.2, 0.4, 0.6七个参数值在雷诺数Re=3.27×106算例中进行精细化标定。参数值取0.2时与实验数据拟合最为准确，进一步在较大雷诺数范围进行测试，表面粗糙度h=3.3 μm，Re=2.37×106与Re=3.27×106的转捩起始位置偏差都得到了有效修正，转捩起始位置与风洞实验符合较好(见图6)。

3.2 横流转捩算例

前文基于固定粗糙度的后掠翼算例对横流模型参数进行了标定，本节对三种粗糙度、不同雷诺数条件下的后掠翼以及15°攻角椭球体和DLR-F4翼身组合体进行计算，以验证横流模型参数的适用性。

3.2.1NLF(2)- 0415后掠翼

NFL(2)- 0415无限展长后掠翼在-4°攻角下，机翼上表面的转捩由横流不稳定性主导，是低速横流转捩典型算例。选取该算例，采用标定后的模型对变粗糙度的风洞实验[19]转捩位置进行预测，验证模型在不同粗糙度下横流转捩模拟能力。攻角为-4°，后掠角45°，雷诺数范围为Re=1.9×106～3.8×106，网格量约50万，物面第一层网格法向间距y+<1，壁面粗糙度(h)根据风洞模型加工精度设置为0.5 μm,3.3 μm,9 μm，来流湍流度Tu∞≈0.1%，νt/ν=5，前缘边界层远场湍流度Tu≤0.02%。

图7是三种粗糙度、多雷诺数条件下的计算结果，预测的转捩起始位置随粗糙度和雷诺数变化规律与风洞实验相同，粗糙度促进转捩，增大雷诺数转捩靠前。高雷诺数下模型预测的转捩起始位置和实验符合较好，低雷诺数下预测的转捩起始位置相比实验值靠前。

图7 不同粗糙度下NFL- 0415后掠翼的实验 和计算结果对比[13,19]Fig.7 Modeling and experimental results of different surface roughness values[13,19]

3.2.2带倾角的标准椭球体

采用6:1标准椭球体[20]对重新标定的横流模型在大攻角条件下的横流转捩预测能力进行验证。算例选取攻角15°、雷诺数6.5×106的典型状态进行测试。网格量为200万，物面第一层网格法向间距y+<1。来流湍流度按衰减公式[12]进行设定，保证靠近椭球体的来流Tu≈0.1%，黏性比νt/ν=5，壁面粗糙度取默认值[13]h=3.3 μm。

图8为实验测量以及模型预测的椭球体表面摩阻系数分布云图。图8由上至下依次是实验结果、γ-Reθt计算结果、Chant平台横流模型计算结果以及文献计算结果[13]。在高雷诺数、大攻角且横流不稳定性占主导的情况下，原始γ-Reθt模型的预测转捩阵面与实验存在较大差别，而Chant平台标定后的横流模型能较准确预测椭球表面的横流转捩阵面，转捩区Cf值比实验结果偏低，与文献横流模型[13]预测能力相当。图9为沿长轴周向展开后的摩阻系数分布，转捩模型预测横流转捩阵面与稳定性分析和风洞实验符合较好。

图8 椭球体表面摩擦系数分布云图Fig.8 Cf contours on spheroid

图9 Chant平台横流模型模拟表面摩擦力云图Fig.9 Cf contour on spheroid: Chant modeling, stability theory and experimental result

3.2.3DLR-F4翼身组合体

DLR-F4翼身组合体是在欧洲跨声速风洞中进行的实验。风洞实验[21]采用温敏漆技术显示层/湍流区域以及转捩位置。图10、图11中实验照片的明暗界线即为转捩位置。风洞实验Ma=0.785，机翼上表面为跨声速流动区域。翼面有转捩发生，上翼面靠近翼根部分的转捩由横流不稳定性主导，靠近翼尖区域的转捩由T-S不稳定性主导。选取两个攻角状态：-2.59°，-0.87°，雷诺数Re=6×106，网格量约为320万，物面第一层网格法向间距y+<1，来流湍流度Tu∞≈0.1%，保证边界层远场湍流度自由衰减至Tu≤0.05%，黏性比νt/ν=1，表面粗糙度设置为0.15 μm[5]。

图10 -2.59°攻角下的转捩位置示意图Fig.10 Transition location on DLR-F4 with AoA of -2.59°

图11 -0.87°攻角下的转捩位置示意图Fig.11 Transition location on DLR-F4 with AoA of -0.87°

图10、图11是不同攻角下DLR-F4风洞实验和数值计算的转捩位置对比。转捩模型能够较准确预测靠近翼根处的横流不稳定性占主导的转捩区域。图11所示机翼中段部位，数值计算同实验存在差距，现有模型预测的T-S波转捩过早发生。

4 结 论

本文横流转捩模型不确定度量化分析与参数研究结论如下：

1) 参数调整对转捩不确定度贡献明显。在参数cCF,h与cθt给定范围后，转捩区Cf不确定度较大，层流区为0。低速平板转捩区Cf不确定度最大达90%，后掠翼转捩区不确定度最大达189%。

2) 根据参数灵敏度指数分析结果，在横流转捩中，参数cCF对Cf和转捩起始位置的影响要大于参数cθt的影响。应选取横流参数cCF对模型进行标定。粗糙度h作为固有参数也会影响横流转捩，在风洞实验与飞行试验中应进行精密测量。

3) 以不确定度及敏感性分析结果为指导进行重新标定后的横流模型对变粗糙度NFL- 0415翼型、带倾角的6:1标准椭球体和DLR-F4翼身组合体的横流转捩能够进行较好地预测。

基于参数不确定性的横流转捩模型不确定度与参数敏感性研究，能够量化模型参数对转捩的影响，提供转捩结果误差带定量分布，具有工程指导价值。参数导致的模型不确定度和敏感性定量结论，对研究者进行模型使用、标定与修改具有参考价值。研究方法具有通用性，可用于各类转捩/湍流模型的不确定度分析，甄别模型的关键参数，指导模型的精细化调试，对模型的改进与工程应用有所裨益。