大型低轨航天器与星座卫星的碰撞风险研究

李翠兰，欧阳琦，陈 明，刘 静

(1. 中国科学院国家天文台，北京 100012；2. 中国科学院大学，北京 100049； 3. 北京航天飞行控制中心，北京 100094)

0 引 言

自20世纪90年代以来，微小卫星技术迅猛发展，通信与导航卫星在低地球轨道(简称低轨)上的应用潜力渐渐被挖掘[1-4]。由于低轨微小卫星具有成本低、部署快、时间分辨率高、覆盖范围广、响应速度快、传输时延小等优势，新型商业低轨小卫星星座不断涌现。由于星座卫星数量庞大，随着星座卫星的发射，预计空间目标的数量将快速增长，对长期在轨飞行的低轨航天器产生严重威胁，为航天器的安全管理带来新的挑战。因此，研究星座卫星对航天器碰撞风险的影响至关重要。据美国北方天空研究机构(Northern Sky Research，NSR)对全球中低轨通信卫星星座的统计分析，全球至少有16家公司已经对外公布其星座计划，星座卫星数量几十到几千不等，高度主要集中在1000～1500 km和600 km左右[5]，为保证全球覆盖率，部分星座轨道设计为极轨道，如，铱星二代星座、OneWeb星座、Telesat LEO星座、LeoSat星座以及我国的鸿雁星座，其余星座也设计了大倾角轨道。目前已有公司开始逐渐部署低轨星座卫星。如，全球卫星电信网络的美国初创公司(OneWeb)在今年2月份首次发射了6颗卫星[6]。太空探索技术公司(Space Exploration Technologies Corp, SpaceX)在今年5月成功将其星链(Starlink)星座的第一批60颗互联网卫星送入太空[7]。Space-X一共计划向低地球轨道发射约1.2万颗Starlink卫星。如果这些星座卫星全部发射，且退役或失效后采用无控陨落，则会出现在短时间内有大量卫星进入近地空间，对近地空间卫星安全产生威胁，特别是对长期在轨飞行航天器的影响较大。

中国预计在2022年前后建成空间站，空间站轨道高度约400 km左右，倾角42°～43°，总重量90吨左右，在轨运营10年以上[8]。中国空间站在轨飞行期间极有可能受到星座卫星的碰撞。因此，本文重点研究了星座卫星在退役或失效后无控衰减过程中与中国空间站的碰撞风险。目前在空间目标碰撞风险评估中广泛采用最小接近距离、碰撞概率等评价指标，对应碰撞预警的区域方法(BOX)和碰撞概率方法(PC)[9-11]。

考虑到600 km以上的圆轨道卫星，受大气阻力等非保守力的影响较小，其轨道衰减缓慢，与大型低轨航天器的碰撞风险几乎为零。本文以600 km高度星座为研究对象，通过计算交会时间、交会次数、碰撞概率等参数，对星座与大型低轨航天器的碰撞风险进行评估，为空间站的理论轨道设计、发动机和燃料的设计、以及碰撞规避控制相关参数的设置提供有益参考。

1 星座轨道演化分析

由于目前还没有规模较大的低轨星座。因此在分析星座卫星对空间站碰撞风险时，结合目前对外公布的星座计划和星座轨道演化特性，首先构建了一个具有156颗小卫星的、高度约600 km的星座，采用数值积分的方法，分别对每颗卫星进行了轨道演化分析；其次，选取已经发射的SpaceX的Starlink星座第一批60颗卫星，采取同样的方法进行了分析。

1.1 低轨小卫星星座构建

星座的组网方式模拟了Walker类星座的组网方式[12]，建立了具有156颗小卫星的均匀对称星座。如图1所示，分别部署在13个轨道面，每个轨道面均匀分布12颗卫星。

图1 低轨卫星星座卫星分布Fig.1 The distribution of constellation satellites

星座卫星的部分参数值参考了OneWeb星座卫星参数[6]，其它参数按照卫星星座分布设置。卫星面质比约0.01 m2/kg，轨道高度为600 km，偏心率为零，轨道倾角约87°，近地点幅角为零，升交点赤经为360[i/12]/13，平近点角为360[i/13]/12-360[i/12]/13，i为卫星编号(i=1,2,3,…,156)。

假设该星座从2019年1月1日退役后无控飞行，受大气阻力的影响逐渐衰减陨落。

1.2 轨道演化动力学模型设置

对于轨道高度600 km及以下的空间目标，摄动影响因素主要包含地球质点引力摄动、地球非球形引力摄动、日月引力摄动、其它大行星引力以及大气阻力摄动等[13]。其中，由于轨道预报时间较长，太阳活动和地磁活动均取其平均值，大小参考了美国CelesTrak网站发布的2020年到2026年太阳活动和地磁活动预报参数的平均值。表1给出了本文在轨道演化过程中采用的动力学模型及参数。

1.3 低轨小卫星星座轨道演化分析

以2019年1月1日0时0分0秒为轨道演化的时间起算点，采用数值积分的方法，分别对星座卫星进行轨道演化，并计算了星座卫星与大型低轨航天器可能发生碰撞的时间区间。

表1 动力学模型及参数Table 1 Models and parameters for orbital propagation

假设大型低轨航天器正式运行起始时间t0为2022年1月1日0时0分0秒，且长期运行在420 km到380 km的高度区间，即当轨道高度由420 km衰减到380 km，则进行轨道维持，将轨道抬高到420 km，在下文中将该高度区间称为小卫星与大型低轨航天器可能发生碰撞的高度区间，小卫星由420 km逐渐衰减到380 km的飞行时间称为小卫星与大型低轨航天器可能发生碰撞的时间区间。

图2描述了每颗小卫星与大型低轨航天器可能发生碰撞的时间区间，横坐标为星座卫星编号，纵坐标为小卫星与大型低轨航天器可能发生碰撞的时间t，该时间为相对于2022年1月1日0时0分0秒的积年。图3描述了每颗小卫星与大型低轨航天器可能发生碰撞的持续时间Δt，横坐标为星座卫星编号，纵坐标为小卫星与大型低轨航天器可能发生碰撞的持续时间Δt。从图2、图3可以看出，星座卫星在大型低轨航天器正式运行约第5.9年后，可能与大型低轨航天器发生碰撞，持续时间约1.1～1.4年，且时间相对集中。由此可知，如果小卫星轨道初始高度设置一致，则导致在1～2年的短时间内，星座卫星与大型低轨航天器存在较大的潜在碰撞风险。

图2 碰撞时间分布Fig.2 The distribution of collision time

1.4 Starlink星座卫星轨道演化分析

目前已发射的星座卫星，在600 km左右高度且卫星数量较多的仅有SpaceX发射的Starlink星座首批60颗互联网卫星。卫星轨道高度约550 km左右，偏心率约0.001左右，轨道倾角约53°左右，如图4所示。

图3 碰撞持续时间Fig.3 The duration time of collision

图4 Starlink星座首批60颗卫星分布Fig.4 The distribution of 60 Starlink satellites

本文以Starlink星座首批60颗卫星2019年7月9日发布的双行轨道根数作为初始轨道。为保证Starlink星座卫星在轨道演化过程中与大型低轨航天器使用大气环境参数一致，减少由大气环境参数不一致造成的轨道误差，本文将双行轨道根数转换为J2000.0惯性坐标系位置速度，然后再使用第1.2节的轨道演化动力学模型进行轨道外推。面质比通过分析双行轨道数据取0.004 m2/kg。

以双行轨道根数中历元时间为轨道演化的时间起算点，采用数值积分的方法，分别对卫星进行轨道演化，并计算了Starlink星座卫星与大型低轨航天器可能发生碰撞的时间区间。Starlink星座卫星轨道演化结果分析过程中，计算卫星与大型低轨航天器可能发生碰撞的时间区间t和持续时间Δt，时间同样取相对于2022年1月1日0时0分0秒的积年。图5描述了Starlink星座每颗小卫星与大型低轨航天器可能发生碰撞的时间区间t，横坐标为星座卫星编号，编号规则为按双行轨道根数中卫星编号升序从1编到60，纵坐标为小卫星与大型低轨航天器可能发生碰撞的时间t。从图5可以看出，有51颗卫星在大型低轨航天器正式运行约第11～13年间可能与大型低轨航天器发生碰撞，且时间相对集中，其余9颗卫星时间不等，经分析主要是由于轨道高度相差较大引起的，其余9颗卫星均未到达550 km高度。图6描述了每颗小卫星与大型低轨航天器可能发生碰撞的持续时长Δt，横坐标为星座卫星编号，编号规则同图5，纵坐标为小卫星与大型低轨航天器可能发生碰撞的持续时间Δt。从图6可以看出，持续时间约1～2年。轨道演化结果与上一节星座演化分析结果基本一致。两星座与大型低轨航天器可能发生碰撞的时间相差较大，主要是由于星座卫星面质比相差较大引起的，与轨道演化特性吻合，即在相同大气环境下面质比大的星座卫星衰减较快。

图5 碰撞时间分布Fig.5 The distribution of collision time

图6 碰撞持续时长Fig.6 The duration time of collision

2 碰撞风险评估方法简介

本节对碰撞风险评估方法进行简要介绍，主要包括BOX方法和碰撞概率两种算法[9-11]。

2.1 BOX方法

由于对空间目标轨道确定和预报都存在一定的误差，因此碰撞不可能通过轨道预报绝对地确定，而只能是确定一个极有可能发生碰撞的区域。以相互交会的两个空间目标在其中一个空间目标U-N-W坐标系内的最小距离作为判据，当其中一个目标进入主目标的距离门限范围内时，将作为危险目标。U-N-W坐标系的定义为：U方向为主目标速度矢量方向，N方向为与U方向垂直并指向轨道外法线方向，W方向与U-N方向构成右手系，如图7所示。

图7 BOX方法示意图Fig.7 The BOX method

2.2 碰撞概率算法

碰撞概率计算方法通常基于以下假设：能够获得两个航天器最接近时刻在惯性系中的位置、速度和位置协方差矩阵；两目标均可等效为半径已知的球体；在交会期间两目标的运动都是直线运动，没有速度不确定性；两目标的位置不确定性都服从三维正态分布，可以由分布中心和位置误差协方差矩阵描述，且两目标位置误差协方差矩阵不相关。

危险目标假定为半径为L1的球形物体，在最接近点J2000.0惯性坐标系位置为r1，在U-N-W坐标系的位置协方差矩阵为B1；主目标假定为半径为L2的球形物体，在最接近点J2000.0惯性坐标系位置为r2，在U-N-W坐标系位置协方差矩阵为B2。

则定义碰撞距离为

d=L1+L2

(1)

相对位置矢量为：

r=r1-r2

(2)

由于r1和r2相互独立，因此r对应的协方差矩阵为：

(3)

式中:M1和M2分别为两目标U-N-W坐标系到J2000.0惯性坐标系的转矩阵。

两目标的位置误差满足三维正态分布，则其碰撞概率如下所示：

(4)

以垂直相对速度矢量的平面作为交会平面，建立交会坐标系。交会坐标系定义：以主目标的质心为坐标原点，z轴指向过最近点时的相对速度方向，x轴指向复合位置误差椭球在交会平面上投影椭圆的主轴方向，y轴由右手规则得到。

在交会坐标系中，危险目标的位置为：

r′=Mr

(5)

式中：M为J2000.0惯性坐标系到交会坐标系的转换矩阵，忽略由相对速度不确定性所带来的影响，把它看作为常数矩阵。

同样，在交会坐标系中，误差协方差矩阵变为：

B′=MBMT

(6)

不考虑相对速度方向(即z轴方向)的位置不确定性，于是，碰撞概率PC可简化为在交会平面上，危险目标进入主目标碰撞圆内的概率,即

(7)

3 碰撞风险分析

3.1 初始轨道参数设置

本文构建了大型低轨航天器的初始轨道参数，假定初始轨道历元为2022年1月1日0时0分0秒，轨道高度为400 km，长期飞行在420 km到380 km之间，具体参数见表2。

表2 轨道参数Table 2 Orbital parameters

3.2 低轨小卫星星座碰撞风险分析

依据星座卫星和大型低轨航天器的轨道演化结果，采用BOX方法和碰撞概率两种方法，分别计算每颗星座卫星与大型低轨航天器潜在交会时间段内的接近距离和碰撞概率，并对风险进行评估。

3.2.1BOX方法碰撞风险分析

依据BOX方法，假设以大型低轨航天器为中心，以文献[15]国际空间站的-72 h门限作为U-N-W三方向黄色预警门限25 km×2 km×25 km，小于48 h门限作为红色预警门限4 km×0.5 km×4 km。图8、图9分别给出了每颗卫星与大型低轨航天器交会并进入预警门限范围的次数。从图8、图9可以看出，进入黄色预警门限总计约2629次，进入红色预警门限总计约1679次，平均每颗卫星与大型低轨航天器交会并进入红色预警门限的次数可达10次左右。

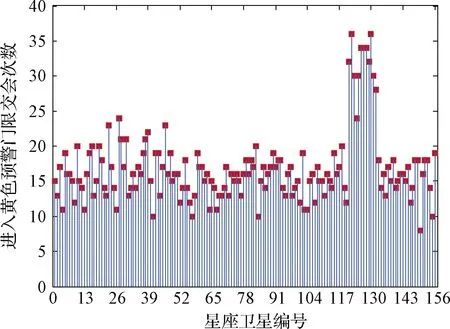
图8 进入黄色门限的交会次数Fig.8 The number of yellow alert conjunction

图9 进入红色门限的交会次数Fig.9 The number of red alert conjunction

3.2.2碰撞概率方法碰撞风险分析

依据碰撞概率方法，假设两目标在各自U-N-W坐标系的误差协方差均为σU=1.5 km，σN=0.5 km，σW=0.5 km，dcollision=0.01 km，分别计算最近距离时刻两目标的碰撞概率。依据目前国际常用碰撞概率门限，假设黄色预警门限为10-5，红色预警门限为10-4。图10给出了不同碰撞概率范围内总的交会次数，横坐标为碰撞概率的对数，纵坐标为不同碰撞概率范围内总的交会次数。图11给出了每颗卫星与大型低轨航天器交会并进入红色预警门限范围的次数。从图10、图11可以看出，进入黄色预警门限总计13次，进入红色预警门限总计7次，大于10-10的约有55次。与BOX方法相比，使用碰撞概率作为门限，交会次数显著降低,主要是由于两种评估方法的差异造成的。BOX方法仅考虑了空间两目标的位置和轨道预报误差。碰撞概率不但考虑了轨道预报误差，还同时考虑了空间交会物体的轨道特征、交会时刻双方的距离、交会角度以及交会时刻的相对速度以及参数之间的相互关系，是一种更客观、全面和精确的碰撞判据。BOX方法与碰撞概率方法各有优缺点，碰撞概率方法可以得到更加合理的几何相对关系，减少碰撞预警中的“虚警”问题；当轨道精度较差时，碰撞概率判定法可能会失效(计算得到的概率偏小)，所以在轨道精度较差时需要结合BOX方法进行综合评估，减少碰撞预警中的“漏警”问题[14]。

图10 碰撞概率计算结果交会次数统计Fig.10 The number of conjunction for collision probability

图11 碰撞概率值进入红色门限的交会次数Fig.11 The number of red alert conjunction

国际空间站自1998年发射以来，已经进行了20多次成功的规避[15]。相对于国际空间站平均每年规避1次的频率而言，星座与大型低轨航天器碰撞仿真计算结果约1.5年之内规避7次，显然是不可接受的。

3.3 Starlink卫星碰撞风险分析

采用与第3.2节相同的方法对Starlink星座卫星和大型低轨航天器的碰撞风险进行了评估。

3.3.1BOX方法碰撞风险分析

假设BOX方法预警门限与第3.2.1节中相同，图12、图13分别给出了每颗卫星与大型低轨航天器交会并进入预警门限范围的次数。从图12、图13可以看出，进入红色预警门限总计997次，进入红色预警门限总计636次，每颗卫星与大型低轨航天器交会并进入红色预警门限的次数可达10次左右，与第3.2.1节碰撞风险分析结果基本一致。

图12 进入黄色门限的交会次数Fig.12 The number of yellow alert conjunction

图13 进入红色门限的交会次数Fig.13 The number of red alert conjunction

3.3.2碰撞概率方法碰撞风险分析

假设碰撞概率方法预警门限与第3.2.2节中相同，图14给出了不同碰撞概率范围内总的交会次数，横坐标为碰撞概率的对数，纵坐标为不同碰撞概率范围内总的交会次数。图15给出了每颗卫星与大型低轨航天器交会并进入红色预警门限范围的次数。从图14、图15可以看出，进入红色预警门限总计3次，碰撞概率值大于10-10的约有21次。与第3.2.2节碰撞风险分析结果基本一致，星座中约有5%的卫星进入红色预警门限。

图14 碰撞概率计算结果交会次数统计Fig.14 The number of conjunction for collision probability

图15 碰撞概率值进入红色门限的交会次数Fig.15 The number of red alert conjunction

4 结论与展望

本文以600 km高度星座和大型低轨航天器为研究对象，通过计算交会时间、交会次数、碰撞概率等参数，分别对构建的轨道高度为600 km小卫星星座和已经发射的SpaceX的Starlink星座第一批60颗卫星与大型低轨航天器的碰撞风险进行了评估分析，得到以下结论：

1) 星座轨道演化分析表明，星座卫星与大型低轨航天器可能发生碰撞的时间相对集中，持续时间约1～2年。

2) BOX方法计算结果表明，如果取U-N-W三方向相对距离4 km×0.5 km×4 km为红色预警门限，每颗卫星与大型低轨航天器进入红色预警门限的交会次数约10次左右。

3) 碰撞概率计算结果表明，如果取碰撞概率10-4为红色预警门限，约有5%的卫星进入红色预警门限。

由此可见，星座如果采取无控衰减陨落，将对大型低轨航天器在短时产生较大的威胁。本文的研究成果可为大型低轨航天器相关参数的设计和预警规避提供技术支撑，也可为小卫星星座的设计提供参考。