采用伪速度冲击响应谱评估蜂窝夹层板破坏边界

洪润民，李 响，丁继锋

(1.北京理工大学宇航学院，北京 100081； 2. 北京空间飞行器设计总体部，北京 100094)

0 引 言

蜂窝夹层板结构由两层面板和芯层复合而成，具有较高的比强度、比刚度以及较好的隔热、隔振性能，在航空航天领域得到广泛应用，是现代飞行器中的主要承力结构形式。蜂窝夹层结构具有明显的冲击敏感性，冲击破坏是蜂窝夹层结构安全研究中的重要问题[1]。

航天器在工作过程中，需要使用火工分离爆炸装置用于子结构间的分离，如：星-箭分离，火箭级间分离，整流罩分离等。火工冲击载荷具有高频、瞬态和高量级的特点[2]，这是航天器结构面临的最严酷的力学环境之一，能否在火工冲击载荷下保持结构安全是包括蜂窝结构在内的航天器结构安全性评估的重要指标。而火工冲击载荷是一种随时间持续变化的复杂波形，较难在时域和频域内精确复现。针对这一情况，冲击响应谱(Shock response spectrum，SRS)方法在航天器结构火工冲击安全性评估中得到了较广泛的应用，该方法将一个实际的物理系统分解为多个不同固有频率的单自由度子系统，对每个单自由度子系统进行冲击响应分析计算，将各子系统响应的最大值连接即得到冲击响应谱。冲击响应谱试验目前已成为了大多数航天器结构必做的试验，NASA与美国军方都已设立相关标准[3-4]。

国内在航天器结构的冲击响应谱方面也已进行了一系列的应用和理论研究。严鲁涛等[5]通过冲击响应谱测试了火工冲击环境下整星减冲装置的效果。王锡雄等[6]应用冲击响应谱验证了应用激光激励模拟火工冲击环境的可行性。杨新峰等[7]结合冲击响应谱与应变等效原则提出了一种制定冲击响应谱试验规范的方法。目前国内航天器结构响应谱研究都应用的是绝对加速度冲击响应谱(Absolute-acceleration SRS，AASRS)， AASRS与结构在不同频段下的力学模型之间的关系不明确，不能直接用于结构破坏边界的评估。在利用加速度冲击响应谱确定结构冲击安全包络边界时需要较多的人为经验。

除了加速度冲击谱，文献[8-10]建议用伪速度谱来评估结构在冲击载荷下的安全性。结构通常在低频、中频和高频段呈现不同的力学特征[11]，伪速度谱能直观地表征出这些特征。在国内，韩璐等[12]利用伪速度谱进行冲击实验舱段的环境特性研究，王晓欣等[13]分析了伪速度谱的特性数值，吴震等[14]采用伪速度谱得到了舰用设备的冲击极限载荷。这些研究并没有讨论结构在整个频率范围内的力学模型及相应的破坏边界。Li等[15]探讨了用伪速度谱构建航天器结构冲击载荷下的两类破坏边界问题。在国内航天器结构冲击领域，采用伪速度谱进行结构安全性的研究仍较为少见。

本文以航天器结构中常用的蜂窝夹层结构为研究对象，讨论了结构在低频段、中频段、高频段的力学模型及PVSRS破坏边界，并通过有限元仿真试验对此破坏边界进行了校验、分析和修正。本文的研究对目前常用的加速度冲击响应谱方法起到有益补充。

1 加速度响应谱与伪速度响应谱

冲击响应谱方法将一个实际的多自由度系统分解为一系列的具有不同固有频率的单自由度子系统。各子系统可表示为质量-弹簧-阻尼系统，如式(1)、式(2)所示：

(1)

z(t)=x(t)-y(t)

(2)

式中：m为系统质量,c为阻尼系数,k为弹性系数,x(t)为质量块的绝对位移,y(t)为基座的绝对位移,z(t)为质量块与基座之间的相对位移。

相应的伪速度冲击响应谱V、加速度冲击响应谱A分别为：

(3)

(4)

式中：wn为单自由度系统的固有频率。

在航空航天领域，目前通常采用机械撞击式冲击试验结合绝对加速度冲击响应谱来制定冲击试验规范[16-18]，该方法的优点是操作简单、容易实现、成本较低且现有体系已较为成熟，但其只能给出加速度信息。

与加速度谱相比，伪速度谱包含了更丰富的信息，在对数四坐标系下，伪速度谱除了能给出横坐标频率与纵坐标伪速度的信息外，还能给出与纵坐标伪速度相互成45°关系的位移、加速度信息，因此又叫做对数四坐标冲击响应谱[8]。此外，伪速度谱能反应出冲击载荷下结构在低频、中频和高频段的不同响应特征。在峰值大小为49g，持续时间为22 ms(即一个周期)的正弦波激励下，一个典型的加速度谱及相应的伪速度谱分别如图1所示。从图1可以看出，伪速度谱有较明显的三折线特征，经过圆整后可得三折线谱，其中等位移线、等加速度线分别与纵坐标(即等伪速度线)成正负45°关系[9]。

与图1(a)中的加速度谱相比，图1(b)中的伪速度谱包含了更丰富的信息。图1(a)所示的加速度谱反应出了加速度响应随频率的变化，但仅能看出在75 Hz左右时最大加速度约为82g。而在图1(b)所示的伪速度谱中可以看出，在0～12 Hz的低频段，伪速度谱曲线与位移坐标轴平行，坐标值约为0.04 m，而且在整个频率范围内这是位移响应的最大值；与此类似，在12～45 Hz的中频段，伪速度谱曲线与速度坐标轴平行，坐标值约为3 m/s，这也是整个频率范围内伪速度响应的最大值；在45～10000 Hz的高频段，伪速度谱曲线与加速度坐标轴平行，坐标值约为82g，这也是整个频率范围内加速度响应的最大值。如上所述，伪速度谱自然地反应出冲击载荷下结构在低频、中频和高频段的不同响应特征。

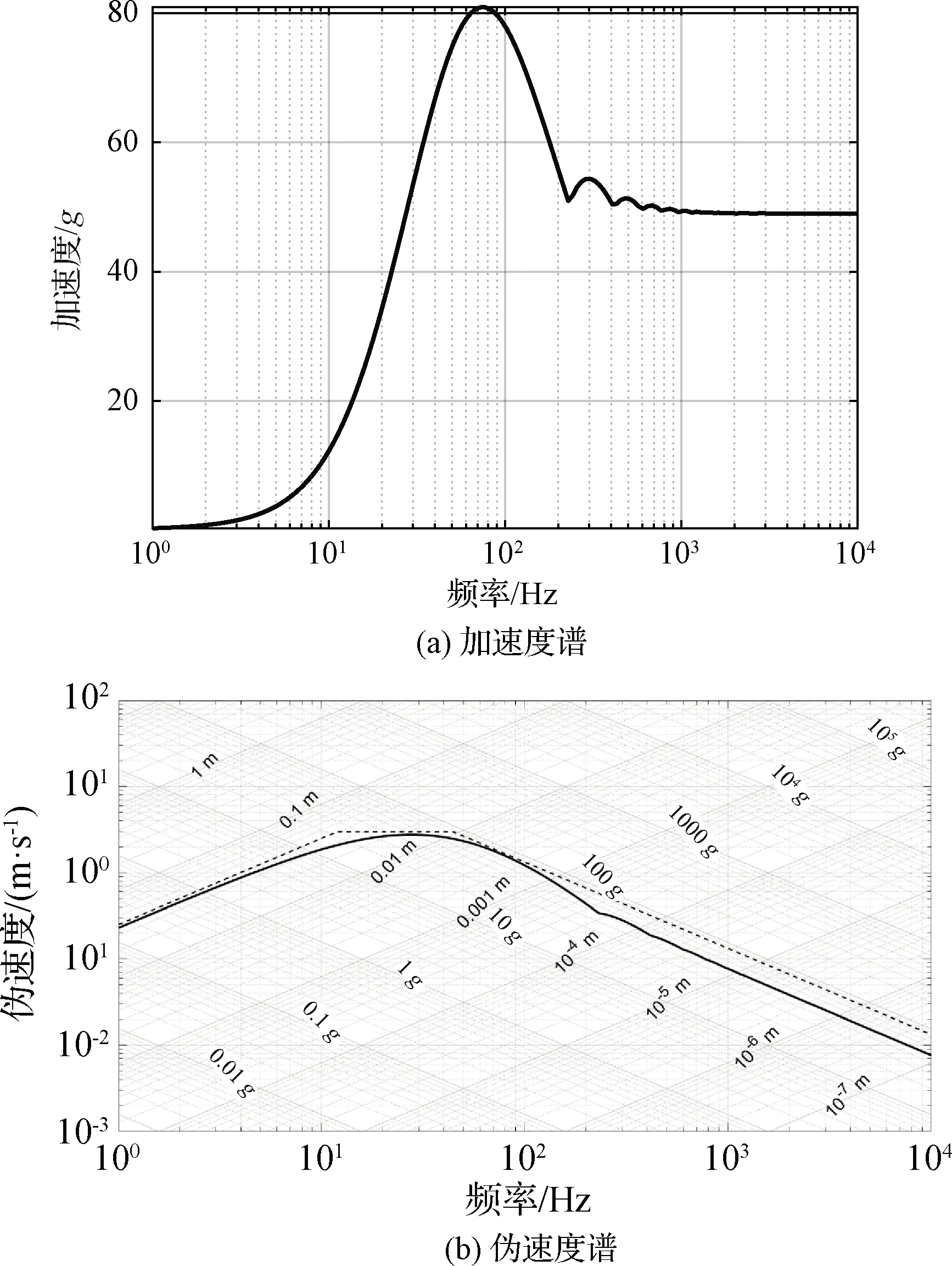
图1 典型的加速度谱及对应的伪速度谱Fig.1 Typical AASRS and corresponding PVSRS

2 三个频段下的力学模型与安全边界

2.1 低频段下的力学模型

设施加于弹簧上的力为F，根据弹性定理最大应力为:

(5)

式(5)表明，在低频段，系统的最大应力取决于基座与质量块之间的相对位移D。

2.2 高频段下的力学模型

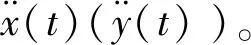
(6)

式中：S为弹簧与质量块连接处的受力面积，A的定义见式(4)。

式(6)表明，在高频段，系统的最大应力取决于最大绝对加速度A。

2.3 中频段下的力学模型

在中频段m和k处于大致相同的量级，此时系统所受的惯性力与弹性力皆不可忽略，故在中频段不能沿用上述的两类模型。在中频段，系统的最大应力σmax与模型的最大速度Vm成正比，二者存在以下关系[8-9]：

σmax=κρcVmax

(7)

此处的最大速度Vmax是系统实际运动中的最大速度而非式(3)中定义的伪速度谱V，设V与Vm间的比值为λ：

(8)

则式(7)可以表示为：

σmax=κρcV/λ

(9)

式中：λ的取值方法参见文献[15]。

式(9)表明，在中频段，系统的最大应力与伪速度V有关。

2.4 伪速度谱表征的结构破坏边界

据临界应力σmax及式(5)、(6)、(9)便可计算出临界位移谱DC、临界伪速度谱VC及临界加速度谱AC：

(10)

(11)

(12)

如何在伪速度响应谱坐标系下利用各临界谱值DC，VC与AC来构造结构的安全边界是一个值得关注的问题。文献[15]中构建了两类边界，以第一类边界为例，如图2所示。图2中实线部分即为破坏边界，若相应的伪速度冲击响应谱有部分曲线明显位于破坏边界上方，则视为结构破坏；若相应的伪速度冲击响应谱被基本包络于破坏边界下方，则视为结构未被破坏。

图2 第一类破坏边界示意图Fig.2 The diagrammatic sketch of Type-I damage boundary

3 冲击载荷下蜂窝夹层结构的破坏边界

本节利用前文构建的结构破坏边界对航天器上常用的蜂窝夹层板在冲击载荷下的安全性进行了讨论，同时针对特定的工况，根据有限元模拟结果对现有的边界进行了适当修正。

3.1 有限元模型

3.1.1结构模型

正六边形蜂窝夹层板是使用最为广泛的夹层板结构之一。在本文中使用的正六边形蜂窝模型进行了如下简化：1)忽略薄胶层对蜂窝夹层板壁厚的影响，在分析建模时将蜂窝板的芯层视为壁厚均匀；2)忽略由芯层制作工艺导致的芯层各边厚度不均匀现象，在分析建模时将芯层厚度视为均匀。

芯层均匀的正六边形蜂窝夹层板的几何参数定义如图3所示，其中蜂窝夹层板的板长为a，板宽为b，板厚度为H，上、下面板厚度为hf，芯层长度为hc，厚度为t，边长为l。面板材料弹性模量为Ef，泊松比为vf，密度为ρf，屈服应力ρfmax，芯层材料弹性模量为Ec，泊松比为vc，密度为ρc，屈服应力σcmax，上述参数的取值见表1。

图3 蜂窝夹层板的几何参数Fig.3 Geometric parameters of honeycomb sandwich panel

在Abaqus平台下建立的有限元模型见图4，其中，芯层及上、下面板的网格划分均采用的是正四边形壳单元，芯层网格与上、下面板网格间采用Tie连接。

表1 蜂窝夹层板参数表Table 1 ParameterTable of honeycomb sandwich panel

网格尺寸采用以下方法确定：由初始网格尺寸不断缩减为原尺寸的1/2，当缩减前的数值计算结果与缩减后的数值计算结果相差在5%以内时，取缩减前的网格尺寸作为最终确定的网格尺寸。在该有限元模型中，芯层及面板的网格尺寸皆为0.00625 m，芯层网格数量为174560个，上、下面板各有14744个，模型网格总数204048个。

图4 蜂窝夹层板模型Fig.4 Honeycomb sandwich panel model

3.1.2载荷及边界条件

蜂窝板的一个板面完全固支作为边界条件，另一个板面受到与其垂直的半正弦载荷，其峰值为Ps，加载时间为ts。

在对蜂窝夹层板进行冲击载荷有限元模拟时，当结构出现塑性形变时即认为结构破坏。采用了多组(Ps,ts)组合进行结构冲击有限元模拟，具体情况在后文中给出。

需要说明的是，提取有限元计算结果作为冲击响应谱计算的输入时，并非提取整个ts的时间历程，而是提取初始零时刻至某一个单元发生一定程度塑性形变的时刻作为输入的时间历程。同时取第一个发生塑性形变的单元作为采样点。

3.2 计算伪速度谱下的破坏边界

在仿真试验过程中，发现在本文讨论的边界条件及载荷类型下，先出现塑性形变的总是芯层，芯层中的每一个蜂窝结构可近似视为长柱体，且受到轴向的载荷，此种情况下κ为常值1，λ为常值1.47。计算得到m=16.68 kg，c=4770.9 m/s，将k=EcS/hc代入式(10)，则该蜂窝夹层结构的临界位移响应谱、临界伪速度响应谱和临界加速度响应谱分别为：

根据计算结果及两类破坏边界的定义，蜂窝板应该遵循第一类破坏边界，如图5实线所示。

当Ps取6 MPa，ts分别取0.08 ms,0.2 ms,0.4 ms,0.6 ms,0.8 ms,1 ms时，相应的伪速度冲击响应谱，如图5虚线所示。

图5显示，Ps取6 MPa载荷下的一系列临界冲击响应谱皆能被预设的第一类破坏边界包络，但对于本文中的模型及特定工况，在中低频段裕度明显较大。

3.3 破坏边界的修正与校验

为了减少中低频段裕度，得到更贴近的破坏边界曲线。在第一类破坏边界的基础上，在低中频段用DC线取代VC,AC线进行包络，此时的破坏边界由部分的DC线与VC线组成。DC线与VC线的交点频率为f1，在ff1时，破坏边界为VC线。修正后的破坏边界对Ps取6 MPa载荷下的临界冲击响应谱包络情况如图6所示。

图5 第一类破坏边界及Ps取6 MPa时的系列 临界冲击响应谱Fig.5 Type-I damage boundary and critical SRSs for Ps is 6 MPa

图6 修正后的破坏边界及Ps取6 MPa时的系列 临界冲击响应谱Fig.6 Modified damage boundary and critical SRSs for Ps is 6 MPa

由于改变载荷峰值Ps大小，理论上不会改变结构破坏边界，使Ps由原来的6 MPa变为3 MPa、9 MPa，ts仍分别取0.08 ms,0.2 ms,0.4 ms,0.6 ms,0.8 ms,1 ms时，绘制相应的临界破坏冲击响应谱来进一步验证修正后的破坏边界的有效性。Ps取3 MPa和9 MPa的一系列临界冲击响应谱分别如图7、图8所示。由图7、图8可知，随着Ps及ts不同产生的不同的临界冲击响应谱皆能被修正后的破坏边界包络，故对于给定的工况，修正的破坏边界是可行的。

此外，有限元仿真结果也显示出冲击载荷的幅值和频率对临界破坏伪速度谱的影响趋势。图6显示，载荷峰值相同时，载荷频率越小，临界伪速度谱在低频段越接近破坏边界，在高频段越远离破坏边界。图9显示，载荷频率相同时，载荷峰值越大，临界伪速度谱在低频段越接近破坏边界，在高频段越远离破坏边界。因此，在采用伪速度谱确定边界时，应综合考虑载荷和结构的具体情况。

图7 Ps取3 MPa时的系列临界冲击响应谱 及高频破坏边界Fig.7 Modified damage boundary and critical SRSs for Ps is 3 MPa

图8 Ps取9 MPa时的系列临界冲击响应谱 及高频破坏边界Fig.8 Modified damage boundary and critical SRSs for Ps is 9 MPa

图9 ts为0.6 ms时的系列临界冲击响应谱 及高频破坏边界Fig.9 Modified damage boundary and critical SRSs for ts is 0.6 ms

4 总结与展望

采用伪速度谱，构建起了蜂窝夹层结构的破坏边界，并与有限元分析结果进行了对比，得到了以下结论：

1) 相对于航天领域目前常用的加速度谱，本文采用的伪速度谱能更清楚地表征出结构在低频、中频和高频段对分离冲击载荷不同的响应特征。

2) 蜂窝夹层结构的冲击载荷下的有限元模拟结果与伪速度谱边界符合得较好。对于给定的工况，可在目前提出的伪速度谱边界基础上适当调整裕度。

3) 本文采用数值模拟方法校验了伪速度谱能有效地给出蜂窝夹层板在冲击载荷下的破坏边界，是目前常用的加速度谱的一个有益补充，在后续研究中可进一步结合试验数据，探讨将伪速度谱方法用于指导航天器结构冲击试验。