考虑火箭约束的深空探测弹轨道拼接模型
张博戎,马 英,何 巍,容 易,刘竹生
(1. 北京宇航系统工程研究所,北京 100076;2.中国运载火箭技术研究院,北京 100076)
0 引 言
目前,深空探测轨道优化研究大多基于天体引力影响球模型和轨道拼接方法进行,对于飞出地球引力影响球的深空任务,探测器出发条件在初步轨道设计环节一般简化为从地心出发的速度矢量[1-2]。如果考虑地球引力影响球大小尺度,弹轨道拼接将具有更多的自由度和优化空间。
此外,部分研究将深空出发条件限定为“施加逃逸速度脉冲前,探测器位于指定高度近地轨道上的任意一点”[3-5],并对出发点赤纬[6]或停泊轨道倾角进行约束[7],这相当于限制了弹轨道拼接的自由度,但并未进一步解决近地停泊轨道与运载火箭主动段弹道的拼接问题,因此仍具有研究空间。
事实上,对运载火箭主动段弹道设计来讲,受限于火箭发射场地理位置、射向、末级滑行时间等实际约束,探测器从地球引力影响球面或停泊轨道上的出发位置十分有限[8],这些参数也直接影响到弹轨道是否可以成功拼接。目前深空探测轨迹优化理论研究和工程应用中均未详细分析火箭约束对于弹轨道拼接问题的影响规律,并未分析不同火箭约束对于各类深空探测窗口的适应能力,但这些指标却是实际工程任务开展所必须考虑的要素,也有可能影响全局任务规划结果,因而对其进行详细的定量研究十分必要。
实现弹轨道全局设计需要依据具体情况,在优化能力、复杂度、适用性之间加以权衡。运载火箭发射深空探测器不同于临近空间飞行器,不需多次出入大气层,因此有必要对此类情况单独分析[9]。本文对弹轨道拼接过程进行了建模,分析了方程组自由度个数,并研究了弹轨道拼接存在解的变量区间及变化规律,最后提出了一种δ-C3图方法,可以用于一般弹轨道拼接问题是否有解的判断依据。
1 轨道拼接计算模型与自由度分析
一般来讲,运载火箭发射深空探测器会先将有效载荷和火箭末级的组合体送至近地停泊轨道,轨道高度一般在180~400 km范围,随后末级等待合适时机二次点火,使有效载荷得到足够飞出地球引力影响球的速度[10]。
建立弹轨道拼接问题简化模型,本文基于以下3点假设:1)地球引力影响球假设;2)假设近地停泊轨道是半径为6578 km圆轨道;3)逃逸速度脉冲切向假设。
依据以上模型,深空探测弹轨道拼接可以分为两个步骤:第一步是已知深空出发速度,选择合适的双曲线逃逸轨道与近地停泊轨道拼接;第二步是根据停泊轨道选择合适的参数与火箭发射弹道拼接。
1.1 逃逸轨道与停泊轨道拼接问题分析
在地球惯性系中考虑双曲线逃逸轨道与近地停泊轨道(LEO)拼接问题,如图1所示,Z轴为地球自转轴,vdpt为地球惯性系下深空出发速度矢量,其大小方向已确定,但在地球引力影响球面上的拼接点位置可以自由选择。通过平移vdpt矢量,其延伸出的可拼接双曲线轨道有多种选择,这些双曲线轨道的集合是以图中H轴呈中心对称的一簇曲线,例如轨道①和轨道②,即为该簇曲线中的两条。以轨道①为例,其与地球引力影响球(SOI)球面相交于Q点,与停泊轨道相切于P点,P点即是施加逃逸速度脉冲位置。与这一簇双曲线逃逸轨道拼接的近地圆轨道集合关于出发速度地心矢量轴(即图1中H轴)中心对称,且均经过公共点M。

图1 逃逸轨道与停泊轨道拼接示意图Fig.1 Splicing diagram of escape orbit and parking orbit
在Q点建立描述拼接问题的方程组,与拼接方程相关的变量是速度v、位置r、时间t,共7个自由度。其中速度需要严格等于深空出发速度vdpt,占去3个自由度;位置要求大小等于地球引力影响球半径RSOI,占去1个自由度,按文献[11]计算方法,本文取92万千米为地球引力影响球半径;此外,停泊轨道高度为定值和切向加速假设同时也对Q点位置施加了一个额外的等式约束,占去1个自由度。需要注意到,尽管严格来讲,Q点的时间也应当等于深空出发时刻,但是考虑到在地球自转一周的时间范围内寻找发射机会,拼接时刻变化给深空轨道带来的改变十分微小,因此可以认为时间没有约束。
为便于描述约束关系与自由度所代表的实际含义,建立原点在地心O的空间球坐标系,如图2所示。以深空出发速度vdpt方向为z′轴,即天顶方向,以ψ表示仰角。在垂直于z′轴方向建立x′Oy′平面,其上用θ表示方位角,通过r,ψ,θ表征Q点几何位置。

图2 描述自由度的球坐标系定义Fig.2 Definition of spherical coordinate system describing DOF
根据以上判断可知,指定高度停泊轨道约束和逃逸速度切向假设相当于限定了Q点的仰角ψ为定值,其大小可以根据∠MPO和∠POQ求解确定,∠MPO的大小φMP与停泊轨道高度和逃逸速度相关,在后文式(8)中有详细计算过程。∠POQ大小φPQ与停泊轨道高度和引力影响球半径有关,可参考文献[12]由几何关系求解确定。方位角θ可以在0°~360°范围内任意取值。用数学关系描述Q点的约束关系,有方程组关系式(1)。
(1)
方程组(1)共具有2个自由度,其中一个是时间自由度,另一个是方位角的自由度,也可以理解为停泊轨道面绕H轴转角的自由度。由几何关系易知,一旦确定了停泊轨道面绕H轴的转角,就可以直接求解得到P点的停泊轨道六根数,进而考虑停泊轨道与发射弹道的拼接问题。
1.2 停泊轨道与发射弹道拼接问题分析
在方程组(1)基础上,进一步考虑发射场位置,分析发射弹道拼接问题。定义地球惯性系Z轴与停泊轨道对称轴H形成的Z-H平面,设H轴上与M点相对地心O对称的点为N,易知ON指向即为深空出发速度vdpt方向,按Z轴北极向上指向画出Z-H平面示意图。定义θ角为停泊轨道绕H轴所转夹角,其取值范围为[0,2π],θ零点位置对应停泊轨道定义为在Z-H平面内,轨道运行方向从N点转向Z轴南极方向,如图3中N点沿轨道切向箭头所示。

图3 停泊轨道与运载火箭弹道拼接示意图Fig.3 Splicing diagram of parking orbit and launching ballistic
假设发射场位于北半球所在纬度圈,则在地球自转一周时间范围内,针对每一个θ角的停泊轨道,其在天球上都可能存在两个与发射场纬度圈交点,分别是L1-L1′、L2-L2′,其中L1、L2点位于发射场纬度圈上,L1′、L2′点位于停泊轨道上。这两组交点分别代表一条从指定点出发的无偏航发射弹道,分别是:1)L1点发射,I1点入轨,经过降交点E2滑行至M点,随后于P点加速逃逸;2)L2点发射,I2点入轨,经过降交点E2至M点后,于P点逃逸。这两条弹道虽然达到同样的停泊轨道,但是其发射时刻、射向、滑行时间、抵达M点时刻均不同。区别起见,本文以下部分将此同一停泊轨道下的两种发射方案分别称为“升轨发射”和“降轨发射”。
考虑方程组(1)中剩余的2个自由度,其中一个表征为θ角的自由度,在停泊轨道确定后,这一自由度就不复存在。另一个自由度需用于匹配发射场地理经度,因为无法保证L1、L2点的位置在发射时刻恰好与发射场重合,所以必须建立等式关系以满足发射时刻约束式(2)。
αL=α0(L0,t*)
(2)
式中:α0是发射场在时刻t*时的赤经,其同时与发射场地理经度L0相关。αL是依据停泊轨道反算得到的发射点赤经。
求解式(2),得到地理经度与赤经匹配的发射时刻t*后,停泊轨道与发射弹道拼接问题即可全部确定。将以上计算过程代入方程组(1),得到完整描述整段弹轨道拼接问题的方程组(3)。
(3)
式中:t*代表根据式(2)求解得到的发射时刻,tL代表火箭主动段飞行时间,在初步分析中可以认为是定值,tc是火箭滑行段时间,其计算过程会在下文详细分析,th代表火箭逃逸段飞行时间,在双曲线轨道确定后可以直接根据几何关系求解[12],本文不再赘述。
方程组(3)中含有一个自由度,将这一个自由度理解为停泊轨道面绕H轴旋转的角度θ,当θ确定后,停泊轨道的轨道倾角和升交点赤经即可直接由球面几何关系求解式(4)~式(5)确定。
i=arccos(sinθcos|δM|>)
(4)
Ω=αM+arctan(tanθsin|δM|>)
(5)
式中:αM,δM分别为停泊轨道公共点M的赤经和赤纬,可以通过vdpt求得。
需要注意,式(4)求解涉及反三角函数值域和求解参数定义域的匹配,在部分区间需要视具体情况增补2π项以满足参数定义域。
由几何关系易知,当轨道倾角和升交点赤经确定后,拼接问题有可能存在0,1,2个解,解的存在性和数量取决于发射场纬度与M点赤纬的大小关系。当发射场纬度绝对值大于M点赤纬绝对值时,停泊轨道圈与发射场纬度圈不相交,因而无解;当发射场纬度绝对值等于M点赤纬绝对值时,停泊轨道圈与发射场纬度圈恰好有一个交点,因而解的数量是1;当发射场纬度绝对值小于M点赤纬绝对值时,停泊轨道圈与发射场纬度圈存在两个交点,因此解的数量为2,分别对应升轨发射和降轨发射。本文第2节中将通过仿真详细讨论解的特点。
当θ角和解的存在性确定后,可以在停泊轨道平面内计算滑行时间,如图4所示。假设运载火箭于L点起飞,飞行至I点进入停泊轨道,随后滑行经过停泊轨道公共点M,最后至P点进入逃逸轨道。

图4 停泊轨道面内弹轨道示意图Fig.4 Schematic diagram of ballistic-orbit splicing in parking orbit plane
这一发射方案的滑行时间tc可通过IP弧段所对应的地心角计算,如式(6)所示。
(6)
式中:T为停泊轨道周期,LM段地心角φLM可由球面几何关系算得,如式(7)所示。
(7)
式中:H0为发射场的地理纬度,i为停泊轨道倾角,正负号取值需分类讨论,此外需判断升降焦点与LM弧段位置关系增减π项以满足反三角函数值域和参数定义域匹配,本文第2节对此有详细说明。
注意到,由于arcsin函数有定义域限制,所以式(7)可能无解。从物理意义上讲,式(7)无解说明选定的停泊轨道不经过发射场纬度圈上方,因而无法在不施加偏航的情况下完成弹道拼接。
式(6)中MP段地心角可通过双曲线逃逸轨道几何参数求得[12],如式(8)所示。
(8)
式中:μ为地球引力常数,RE和hLEO分别为地球半径和停泊轨道高度。
最后,还需根据弹道程序获得LI段地心角,由于同一型火箭达到同一高度停泊轨道所飞行的路线长度近似,所以φLI在初步计算中可以认为是定值。设运载火箭进入停泊轨道的射程为Lr,如式(9)所示。
(9)
将式(7)~式(9)代入式(6),可得到滑行时间的全部计算公式。
根据球面几何关系推导射向A,如式(10)所示。
(10)
至此,与弹轨道拼接相关的全部参数均已求解确定,可以依此进一步计算不同出发条件和发射场约束下的射向与滑行时间。
2 运载火箭射向与滑行时间匹配规律分析
已知深空出发速度vdpt大小和其对应的停泊轨道公共点M赤纬δM,就能求解确定所有θ角停泊轨道对应的发射参数。需要注意到,根据δM与发射场地理纬度H0的大小关系不同,需要对该问题进行分类讨论。如果δM高于发射场纬度,则在所有停泊轨道倾角取值时,拼接问题均存在两个解,如果δM低于发射场纬度,则在停泊轨道倾角为部分取值时无解或只有一个解。此外,当M点与发射场分别位于南北同半球或异半球时,停泊轨道升降交点E1、E2与LM段位置关系不同,因而LM段地心角计算式(7)也须进行分类讨论。以发射场位于北纬28.5°为例,针对不同δM取值可以按表1分类讨论,第2.1~2.4节将分别计算这四类情况。

表1 不同M点赤纬取值范围对应轨道形式Table 1 Orbital status correspond to different range of M declinations
2.1 停泊轨道公共点纬度高于发射场且位于异半球
假定深空出发速度vdpt大小为10 km/s,M点赤纬δM为-40°,与发射场异半球且高于发射场地理纬度。入轨位置关系见图3。
在此类情况中,所有绕H轴旋转的停泊轨道均在天球上与发射场纬度圈有两个交点,由式(4)、式(5)可以计算θ角与停泊轨道倾角、升交点赤经的关系,如图5所示。

图5 停泊轨道轨道倾角、升交点赤经随θ角变化曲线Fig.5 Correlation curve of RAAN and inclination of parking orbit expressed by θ
从图5可以看出,升交点赤经与θ角一一对应,在θ绕H轴旋转一周时,停泊轨道升交点也恰好旋转一周。与此同时,轨道倾角可唯一确定,随θ呈类正弦波动,最小值与出发速度方向赤纬相等,最大值对应轨道面与最小轨道倾角面重合,旋转方向相反。此图进一步说明了方程组(3)所包含的自由度关系,其既可以用θ角表示,也可以用停泊轨道的升交点赤经或轨道倾角来描述。本文采用θ角来表征这一自由度,原因是θ角既可以与每个停泊轨道一一对应,同时也能在0到2π的范围内连续变化,其物理意义相比升交点赤经和轨道倾角更为明确。
根据式(6)~式(9),可以计算不同停泊轨道对应的火箭末级滑行段地心角大小,如图6所示。

图6 运载火箭末级滑行段地心角随θ角变化曲线Fig.6 Correlation curve between rocket’s coasting angle and θ
从图6可以看出,滑行时间随θ角呈现周期变化关系。无论是降轨发射还是升轨发射,其最短滑行时间均对应θ角取180°,最大值均对应θ角取0°或360°,且长短滑行时间增减趋势基本保持同步。本类情况中,可达到的最短滑行地心角约为110°,约相当于27 min。另外注意到,升轨发射方案的滑行时间均会大于降轨发射,这是因为M点位于发射场纬度圈南方所致。

图7 运载火箭射向随θ角变化曲线Fig.7 Correlation curve between launching azimuth and θ
进一步根据式(10)计算不同发射弹道对应的射向,如图7所示。从图7可以看出,两种发射方案射向均随θ角表现出周期变化的关系,且当θ角小于180°时,两种发射方案射向关于90°对称,当θ角大于180°时,两种发射方案射向关于270°对称。在本算例中,由于发射场地处北半球,所以短滑行的降轨发射方案射向均为偏南方向,长滑行的升轨发射方案均为偏北射向,即火箭起飞后会经由北极上空再飞至M点。
一般情况下,希望运载火箭射向接近90°,这样可以充分利用地球自转能量,但是对比结果发现,滑行时间短的发射方案射向均为正南或正北,接近90°射向的滑行时间一般都大幅高于最短滑行时间,因此在实际任务中,需要根据火箭滑行时间和射向约束合理选择发射方案,以求在满足拼接条件的情况下实现最大运载能力。
2.2 停泊轨道公共点纬度低于发射场且位于异半球
假定深空出发速度vdpt大小为10 km/s,M点赤纬δM为-10°,与发射场异半球且低于发射场地理纬度。入轨位置关系见图8。
图8中,L1、L2、L1′、L2′、E1、E2等所有点的定义方式均同第2.1节,分别分析停泊轨道轨道倾角、升交点赤经随θ角变化关系,以及升降轨滑行段地心角大小和射向随θ角变化关系,如图9所示。

图9 公共点M赤纬为-10°时各参数随θ角变化曲线Fig.9 Correlation curve between each parameter and θ when M declination is -10°
从图9可以看出,升交点赤经与轨道倾角的变化规律与图5基本类似,但是由于出发速度矢量的赤纬由-40°降低为-10°,所以也使得升交点赤经随θ角的变化速率有所不同,在θ角处于90°和270°附近,停泊轨道升交点赤经会发生快速变化。另外,由于出发速度矢量的赤纬较低,所以停泊轨道轨道倾角取值范围可以进一步扩大,能够在低纬度地区出现更多的发射机会。
此外,由于出发速度矢量所指向的赤纬低于发射场,所以对于倾角小于28.5°的停泊轨道,不存在不施加火箭偏航的发射机会,该类情况下滑行时间无解。在有解的区域,升降轨飞行方案之间的差异也呈现出“从0增大再减小至0”的规律,在升降轨发射方案的交点处,表示停泊轨道与发射场运动轨迹在天球上相切,因而两个解重合,退化为一个解。该例仿真结果与第1节中关于式(3)的理论分析相符。
另外注意到,在滑行段地心角随θ角变化曲线中,由于升轨发射部分弧段的滑行地心角大小超过了360°,所以该情形实际相当于多滑行了一周,与之对应的实际发射方案可以晚一圈再入轨,因此就可能出现“0滑行时间”的解。由式(6)可知,滑行段是否出现零点解与火箭主动段射程和深空出发速度大小相关。
在射向变化方面,与滑行时间的计算结果类似,在停泊轨道倾角小于发射场地理纬度的情况下,射向无解。在有解的区域内,同样与图7呈现出类似的规律,这是由于发射点位于M点北方的假设条件所决定的。不同于第2.1节中情形的是,在升轨发射方案中,接近90°射向可以对应到短滑行时间的飞行方案。
2.3 停泊轨道公共点纬度低于发射场且位于同半球
假定深空出发速度vdpt大小为10 km/s,M点赤纬δM为10°,与发射场异半球且低于发射场地理纬度。本节分析方法同第2.1节、2.2节,但滑行时间计算公式需考虑到位置关系变化所带来的正负变化和反三角函数值域对应关系,因此需对式(7)结果分类讨论,限于篇幅此处不详细说明。
此种情况中,升交点赤经、轨道倾角、升降轨发射射向变化规律完全等同于M点赤纬为-10°时的情形,因为二者的几何关系是关于赤道面对称的。
在滑行段地心角随θ角变化规律中,除基本保持第2.2节中规律外,更可以发现平均值要普遍小于M点赤纬为-10°时的情形。这是因为此例中入轨点偏向发射场所在的北半球,因而其在大多数发射情况下可以实现比南半球入轨更短的滑行时间。
2.4 停泊轨道公共点纬度高于发射场且位于同半球
假定深空出发速度vdpt大小为10 km/s,M点赤纬δM为40°,与发射场异半球且低于发射场地理纬度。分析方法同第2.1~2.3节,滑行时间计算与第2.3节相同,但是升降轨发射对应的滑行段地心角求解的大小关系恰好相反,这是因为停泊轨道共同点M位于发射场北方的原因造成的。
此种情况中,升交点赤经、轨道倾角、升降轨发射射向变化规律完全等同于M点赤纬为-40°时的情形,因为二者的几何关系关于赤道面对称。在滑行段地心角随θ角变化规律中,除保持与第2.1节中相同规律外,更出现了短滑行时间发射选择,这是因为此例中入轨点偏向发射场所在的北半球。
3 考虑约束的弹轨道拼接问题解集范围分析
进一步考虑指定型号运载火箭射向和滑行时间的约束范围,分析固定地理位置发射场对不同出发条件的匹配能力,找出不同停泊轨道中满足约束的解集范围。
假设发射场位于北纬28.5°,第3.1节、3.2节将分别分析考虑具体射向和滑行时间约束下的弹轨道拼接解集范围。
3.1 考虑射向约束的解集范围
由式(10)可知,求解射向过程与vdpt大小无关,因此在分析射向约束下的解集变化时,vdpt大小任意取值即可,令vdpt大小为10 km/s,变换M点赤纬,以δM和θ角为横纵坐标,画出求解得到射向的曲面图。由于射向解集在θ-δM平面内左右对称,且在各自半区也分别关于90°和270°取值对称,所以只考察90°~180°射向范围内的解集变化情况即可知其趋势。分别查看射向约束为90°~105°、105°~120°、120°~135°、135°~150°、150°~165°、165°~180°六种情况下的解集范围,如图10所示。

图10 不同射向约束下解集变化示意图Fig.10 Schematic diagram of solution set variation under different constraints
随着射向约束范围从90°逐步增加到180°,可行域的范围也呈类同心圆状逐步扩大,直至覆盖θ-δM平面的边缘地区。当射向约束涵盖180°时,在任何深空出发速度方向下,均可以找到匹配拼接问题的解。
如果已知运载火箭射向的约束范围,则可以通过射向约束反求可行域的边界点M赤纬值,根据式(2)和式(10),假设射向约束边界值为Acr,则可以反推得到可行域边界点M赤纬表达式,如式(11)所示
δcr=±arccos(sinAcrcosH0)
(11)
从式(11)可以看出,可行域边界点M赤纬的值与深空出发速度大小并无关系,因此可以直接根据运载火箭的射向约束判断其与深空出发速度方向的约束关系。
3.2 考虑滑行时间约束的解集范围
由式(6)~式(9)可知,滑行时间的计算结果同时与vdpt大小、M赤纬、θ角相关,因此无法将其表示在同一幅三维曲面图中。先假设深空出发速度大小为10 km/s,以停泊轨道转角θ和公共点M赤纬为横纵坐标,计算滑行时间曲面,可以分别得到升轨发射与降轨发射的滑行时间曲面图。取滑行时间约束范围为200~1500 s,在θ-δM平面上用黑色阴影区域表示满足约束的解集范围,如图11所示。
从图11可以看出,升轨发射与降轨发射的解集有所不同,升轨发射解集基本处于θ角在小于90°或大于270°的范围,而降轨发射的解集大致处于θ角在90°~270°的范围内,且两者均偏向于M点偏北的部分,这是因为滑行时间的约束使得太靠南方的入轨点都超出了约束上限。
综合考虑升降轨的发射方案,取两者可行域的并集,即为此出发条件下的全部解集。因为一般的深空探测任务地球出发速度矢量不会超过10 km/s,因此分别考虑出发速度大小为2~9 km/s时的可行域变化情况,如图12所示。

图11 升、降轨发射滑行时间曲面及其解集示意图Fig.11 Schematic diagram of coasting time surface and its solution set by ascending/descending launch

图12 出发速度为2~9 km/s时解集变化情况Fig.12 Solution set change when departure speed is 2~9 km/s
当出发速度矢量较小时,在M赤纬方向存在较多解。随着出发速度矢量大小逐渐增大,解集范围向高纬方向移动,也就是说此时如果深空出发方向要求M点的赤纬过于偏南,则无论θ角取何值,均不会存在满足滑行时间约束的发射机会。
4 利用“赤纬-能量”(δ-C3)图描述运载火箭深空发射能力方法
将射向和滑行时间约束下的解集表示为深空出发赤纬和速度大小的函数,并在图上表示存在拼接解的可行域。在某一出发条件下,只要存在可以拼接的停泊轨道,则认为该点处在可行域内。对于滑行时间约束为200 s~1000 s,射向约束为95°~105°的情况,其可行域如图13所示。

图13 滑行时间与射向可行域示意图Fig.13 Feasible domain of coasting time and launching azimuth
从图13可以看出,两部分阴影区域分别对应射向约束和滑行时间约束,重叠区域即为同时满足两种约束的总可行域。可以看出射向约束的变化与vdpt大小无关,且关于δ=0°对称,这与第3.1节中结论一致。
滑行时间约束随着vdpt大小的增大而逐渐减小,并关于δ=H0对称。进一步根据特殊点性质判断可行域边界随速度大小的变化情况,可以推导得到,在vdpt处,临界滑行时间约束对应的赤纬临界值δcr计算如式(12)所示。
δcr|vdpt=H0±(φc+φLI-φMP|vdpt)
(12)
根据式(12),可以省去数值计算判断某点是否存在拼接解,而是直接画出可行域边界曲线,进而快速判断结果。以射向约束为95°~105°,滑行时间约束下限为200 s、上限分别为1000 s~2200 s的情况为例,画出δ-C3图及可行域边界如图14所示。
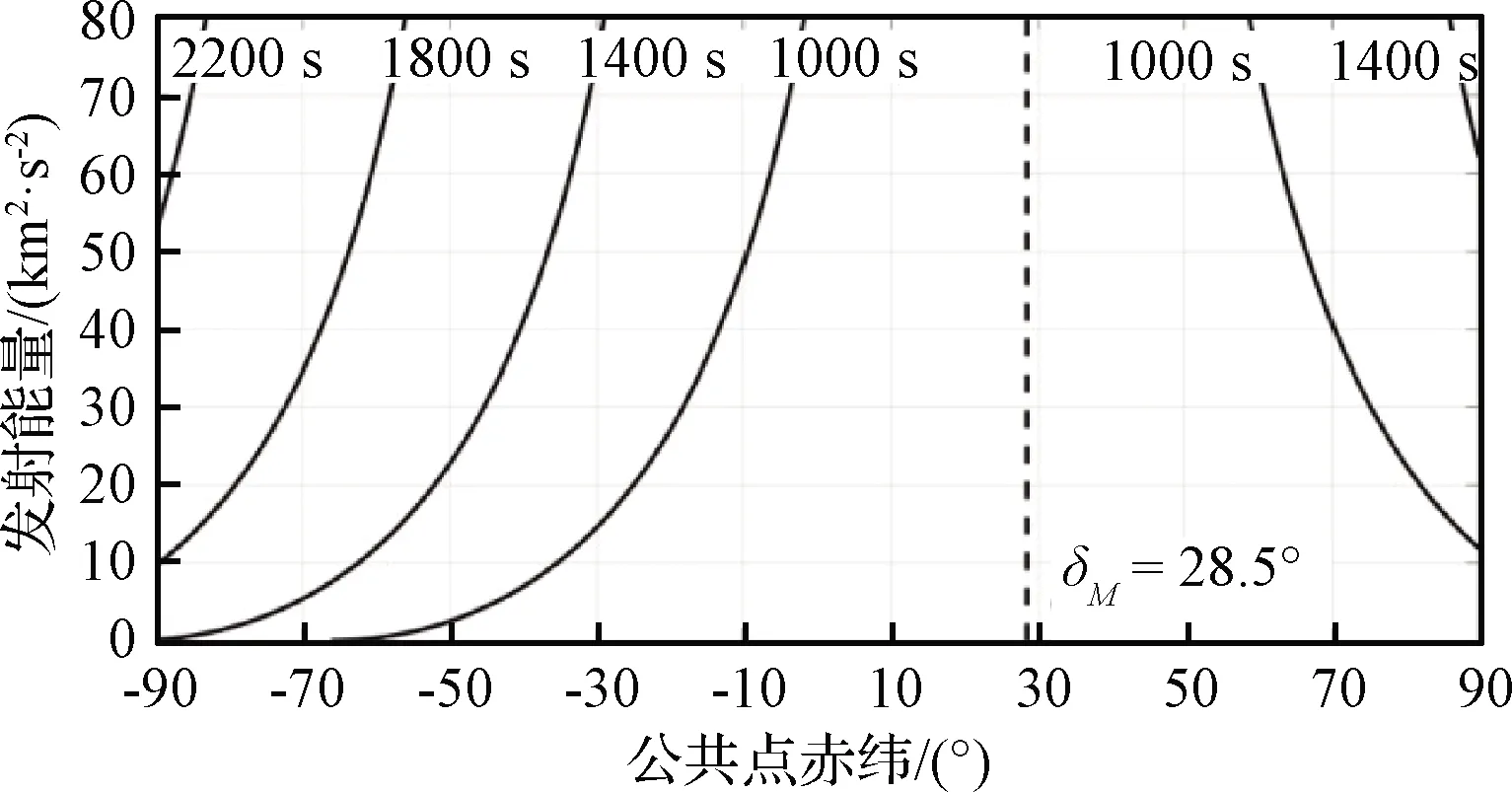
图14 不同滑行时间对应可行域变化图Fig.14 Feasible domain change under different coasting time
随着滑行时间上限的提升,可行域逐步扩大,当滑行时间上限超过1400 s时,δ-C3图右上角已基本不存在无解区域,说明可以胜任所有北半球出发情况。计算发现,当滑行时间上限取至2300 s后,图14范围内所有区域均变为可行域。
针对不同型号的运载火箭和发射场位置,均可根据式(11)~式(12)快速画出其δ-C3图上的可行域范围,进而能够直接判断某一出发条件是否能够在限制条件内完成弹轨道拼接。
对于特定目标和转移方式的深空探测轨道,其出发速度在δ-C3图上也表现为特定区域形式。考虑从地球出发直接转移至火星的探测轨道,在Pork-Chop图上筛选总速度增量小于10 km/s区域,遍历取点并将其表示在δ-C3图中,如图15所示。

图15 在δ-C3图中表示火星探测窗口Fig.15 Representing Mars detection window in δ-C3 diagram
图15中,灰色矩形区域代表95°~105°的射向可行域,左右弧线间包围的区域分别代表1000 s、1400 s、1800 s的滑行时间可行域,滑行时间的可行域关于28.5°呈对称分布。从图15可以看出,代表本窗口轨道方案的所有散点均处在1000 s滑行时间可行域内。若某个其他深空出发窗口在δ-C3图中所代表的散点处在可行域范围外,则说明该方案一定无法满足火箭的发射约束。针对其他探测目标和其他轨道方案的深空探测弹轨道拼接问题,均可以使用此方法进行快速分析。
5 结论与展望
本文基于地球引力影响球模型,建立火箭无偏航情况下的弹轨道拼接模型,推导得到射向和滑行时间的数学表达式,计算并分析了不同出发情形下的弹轨道拼接规律,主要归纳得到以下3点结论:
1) 对于依靠脉冲机动飞出地球引力影响球的深空探测轨道与运载火箭弹道拼接问题,限定停泊轨道高度和发射场地理位置后,该问题具有1个自由度。这一自由度可以表征为停泊轨道绕出发速度过地心轴的转角。停泊轨道升交点赤经和这一转角一一对应,停泊轨道倾角会随其在一定范围内波动,出发点赤纬越低,停泊轨道倾角变化范围越大。
2) 对于深空出发速度在天球上的赤纬不同,弹轨道拼接求解结果呈现不同规律。在停泊轨道公共点赤纬高于发射场地理纬度时,所有转角的轨道面均可以求解得到升轨和降轨两种发射模式;在停泊轨道公共点赤纬低于发射场地理纬度时,部分转角取值时会存在无解情况。公共点赤纬越接近0°,无解区间越大,意味可选择的停泊轨道区间更狭窄。
3) 针对指定型号运载火箭执行的深空发射任务,利用本文提出的δ-C3图方法,可以将火箭在指定射向和滑行时间约束下的发射能力表示为δ-C3图中的特定区域。如果深空出发点位于这一区域内,则意味着弹轨道拼接必然存在满足发射约束的解,反之则必然无解。通过这一方法可以快速判断任一深空出发速度条件是否具有工程上可行的发射机会。
本文研究并未考虑火箭射向、滑行时间等与运载能力的对应关系,可以在此模型基础上进一步补充研究。

