“另类” 的裂项相消法
2020-10-11 07:44:26洪汪宝
数理化解题研究 2020年25期
洪汪宝
(安徽省安庆市第一中学 246004)

在近几年的一些考试中,除了考查上述常见的裂项相消,还出现了不少“另类”的裂项相消,体现了命题老师的一种创新.而对于学生来说,创新制造了不小的麻烦,对学生的思维能力和应变能力要求较高.实际上在利用裂项相消法时,关键要抓住通过裂项达到相消求和的目的.下面举例说明,以期抛砖引玉.

分析将分母由两个因式改为三个因式,但裂项时仍然将一项裂开为两项,注意正负号和系数,达到相互抵消的目的.
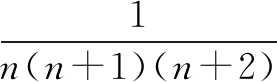
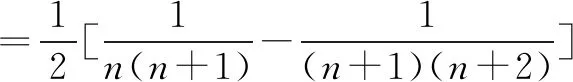
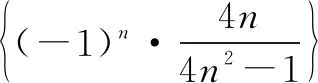
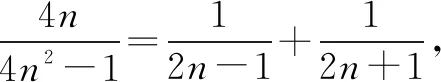
解由分析知
于是当n为偶数时,
当n为奇数时,

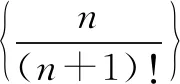
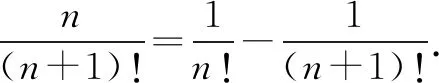

变式求数列{n·n!}的前n项和Sn.
解由n·n!=(n+1)!-n!得
Sn=1×1!+2×2!+3×3!+…+n·n!=(2!-1!)+(3!-2!)+(4!-3!)+…+[(n+1)!-n!]=(n+1)!-1.
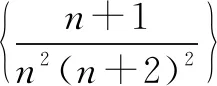
分析分母的次数升高了,但仍然将n2(n+2)2看成两个因式n2与(n+2)2相乘,形式相同,考虑裂项,要注意系数.
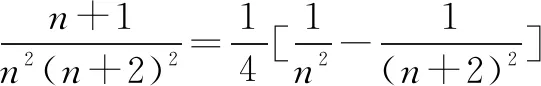
例5 求数列{tann·tan(n+1)}的前n项和Sn.
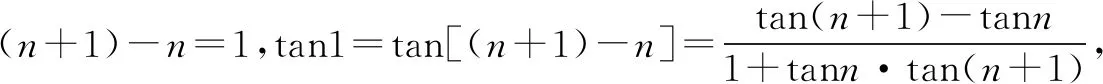
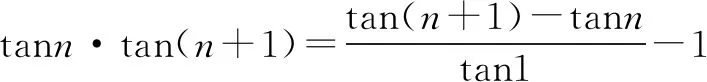
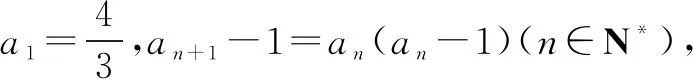
A. {0,1,2} B. {0,1,2,3} C. {1,2} D. {0,2}
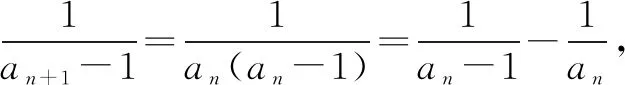
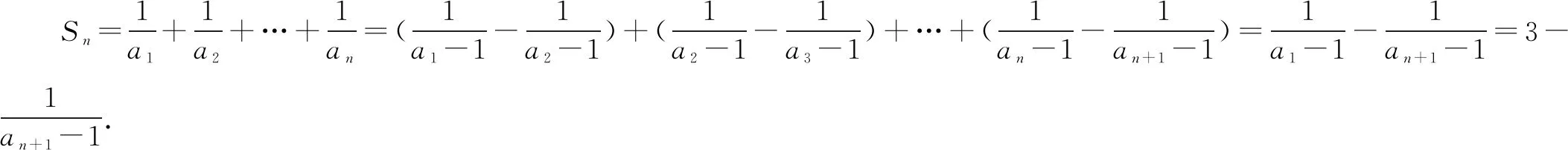
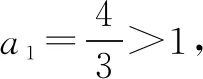
猜你喜欢
中学数学研究(2024年1期)2024-04-29 10:07:30
成功密码(2023年3期)2023-11-08 15:05:43
客联(2021年4期)2021-09-10 15:40:08
中学生数理化(高中版.高二数学)(2020年10期)2020-11-10 08:48:56
中学生数理化·七年级数学人教版(2017年11期)2017-04-23 07:18:05
中学生数理化·高三版(2017年1期)2017-04-20 16:18:34
中学数学杂志(高中版)(2017年2期)2017-03-28 07:51:33
教学月刊·中学版(教学参考)(2016年8期)2016-07-27 08:57:14
消费电子(2014年3期)2014-03-22 18:36:13
数学学习与研究(2012年21期)2012-04-29 01:20:36

