蝗虫切片图像Shannon-Cosine小波精细积分混合降噪

李 丽 朱磊平 梅树立

(中国农业大学信息与电气工程学院， 北京 100083)

0 引言

蝗虫切片图像是研究蝗虫生理结构的有效工具。与普通生物切片图像相同，蝗虫切片图像中的纹理结构呈现为具有多尺度特性的光滑曲线，且边界轮廓不清晰[1-2]。蝗虫切片图像是在显微镜下拍摄得到的，空气中的尘埃及由此带来的光线反射会形成图像中的椒盐和高斯混合噪声。因此，采用常见的典型图像降噪方法很难获得蝗虫切片图像高质量的降噪效果。非线性偏微分方程[3]方法是生物图像处理的常用方法，可实现图像的保边降噪，但该方法缺少多尺度特性，因此对细小纹理保护较差。

小波精细积分法是一种求解偏微分方程的有效方法[4]。该方法可实现偏微分方程空间[5]和时间[6]的多尺度自适应性离散，有效提高了数值算法的效率和精度。近年来，随着同伦技术的引入[7-8]和区间小波[9-10]的提出，小波精细积分法得到不断完善和发展，已在随机振动[11]、土壤侵蚀分析[12]、图像处理[13]、期权定价[14]等领域得到广泛应用。

采用差分法或者单尺度小波数值方法求解二维偏微分方程，离散点总量大，很难满足工程中大数据量问题(如图像处理)求解的要求。因此，将小波精细积分法推广应用于二维偏微分方程的求解具有非常重要的意义。构造二维偏微分方程小波精细积分算法的关键是二维多尺度插值小波算子的构造。利用多尺度小波插值算子对偏微分方程进行自适应离散，得到的常微分方程组可使用基于外推技术的自适应精细积分法[4]直接求解。

本文基于Shannon-Cosine小波[15]构造多尺度小波插值算子，以实现图像的稀疏表达、去除椒盐噪声，基于该算子构造小波精细积分法，以消除图像的高斯噪声和椒盐噪声。

1 Shannon-Cosine多尺度小波变换

1.1 Shannon-Cosine小波及其性质

Shannon-Cosine小波母函数[15]定义为

(1)

其中

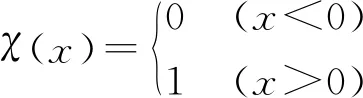
式中N——与支撑区间相关的常数

an——线性组合系数，表示光滑度

χ(x)——Heaviside函数

n、m——函数光滑度参数

显然，函数的支撑区间为[-N/2,N/2]。参数an用来定义函数边界处的光滑度，可通过如下偏微分方程组求得。

(2)

不难验证，Shannon-Cosine小波母函数具有插值特性，即φ(0)=1。将x=N/2 (或者x=-N/2)和x=0代入到式(1)、(2)，可以得到关于参数an的线性代数方程组。

相对于Shannon小波母函数[16-17]，Shannon-Cosine小波母函数具有更好的紧支撑性，如图1所示。

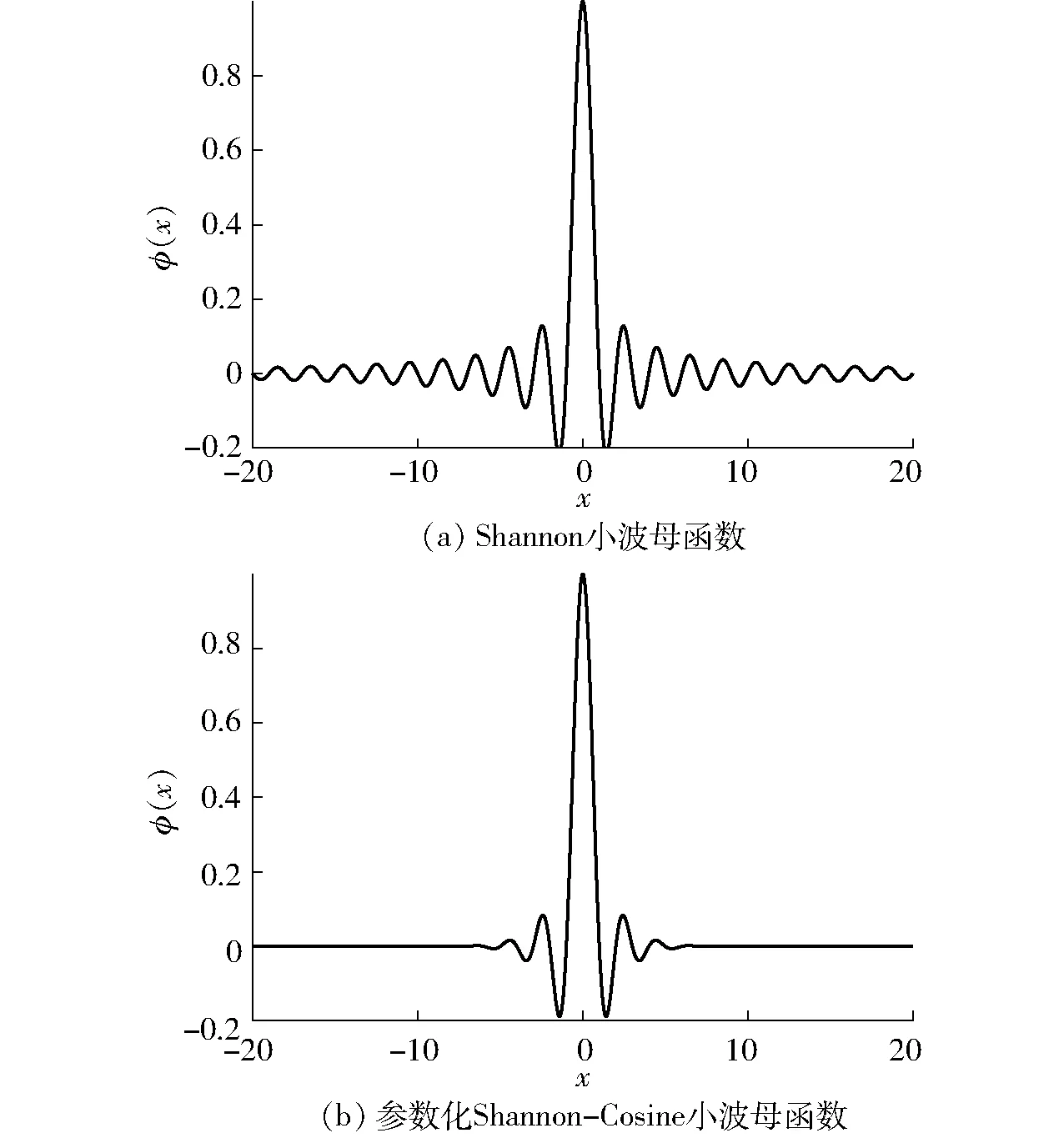
图1 Shannon函数与参数化Shannon-Cosine小波母函数对比Fig.1 Comparison between Shannon function and parametric Shannon-Cosine mother wavelet function

1.2 多尺度插值小波算子

设φ(x)为具有插值特性的小波母函数，通过平移和伸缩得到的函数序列定义为

φj,k=φ(2jx-k)
(k=0,1,…,2j；j∈Z)

(3)

式中j——伸缩系数k——平移系数

φj,k——尺度基函数

对应的小波函数定义为

ψj,k(x)=φj+1,2k+1(x)

(4)

对于函数f(x)∈L2(0,1)，x∈[xmin,xmax]，L表示平方可积的可测函数组成的空间，插值小波变换系数定义为

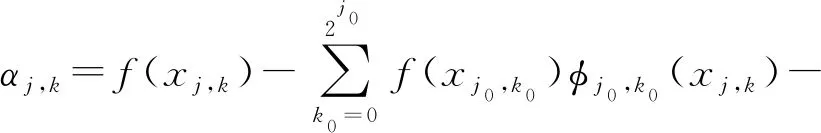
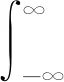
(5)

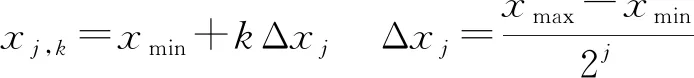
式中αj,k——小波变换系数

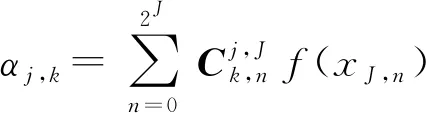
(6)

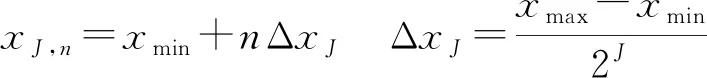
根据插值小波变换系数的定义，有

(7)

其中ψj,k=φj+1,2k+1,利用限制算子的定义得到

(8)

其中

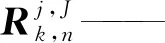
将式(8)代入式(7)，得

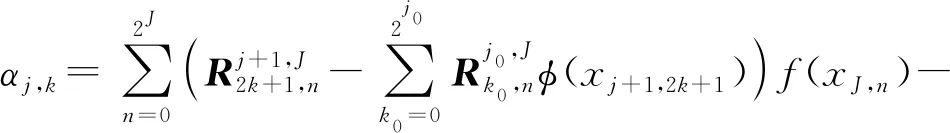
(9)

将式(6)代入式(9)，得

(10)

由式(10)等号两侧对比得到基于Shannon-Cosine小波的多尺度插值小波变换矩阵为

(11)

当j=j0时，得

(12)

利用式(6)，可以方便地计算图像中每个像素点处的插值小波变换系数αj,k。生物医学图像通常可视为分块光滑函数，因此，椒盐噪声点属于光滑图像函数中的不连续点，这便导致椒盐噪声点处的多尺度插值小波变换系数较大。基于该原理，很容易识别图像中的椒盐噪声点，即预先设定阈值为h，对应的软阈值函数定义为

(13)

当图像中某点处的小波系数大于该点处的软阈值时，该点处的图像信息用图像中的其他像素点逼近表达，从而消除了该椒盐噪声。换句话说，稀疏表达本身可消除图像中的椒盐噪声。

2 多尺度Shannon-Cosine小波精细积分法

用P-M模型对图像进行展开，使用小波插值算子实现图像纹理的自适应识别。用Shannon-Cosine小波配置法将偏微分方程离散成常微分方程，在此过程中，小波配置法对纹理实现自动捕捉，即根据图像灰度的变化特点自适应离散，以自适应选取图像的特征点。在纹理处密集选取点集，在平滑处稀疏选点。最后，利用小波精细积分法求解常微分方程得到高精度解，方程组的解即为降噪后图像在该点处的像素值。

2.1 图像处理变分模型

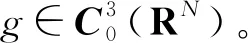
(14)

这个收敛性在L2(RN)空间逐点适用。其中，(g)n*表示g的n次卷积。所以对于每个原始有界图像u0(x)，定义为

Lhu0=gh*u0

(15)

由此可进一步得到(Lh)nu0→Ttu0，这里，Ttu0=u(t,x)，且u(t,x)是一个非线性热传导方程初值问题，P-M模型表示为

(16)

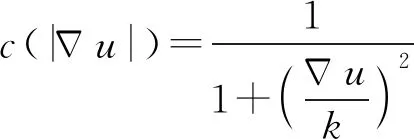
(17)

式中 (x,y)——像素点坐标

t——时间

u(x,y,t)——处理后的图像，简称为u

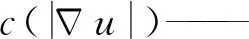
Ω——图像所在区域

∂Ω——图像边界

k——常数，梯度阈值

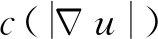
2.2 变分模型的小波精细积分法求解

函数u(x,y)表示像素点(x,y)处的灰度，引入记号

φ(x,y)=φ(x)φ(y)

(18)

则φj,k,l(x,y)=φ(2jx-k)φ(2jx-l),k、l∈Z。由配置法思想, 偏微分方程的解可近似表示为

(19)

将式(19)代入式(16)可得其小波离散格式为

(20)

其中k1=0,1,…,2j;k2=0,1,…,2j,j∈Z。记

(21)

(22)

于是方程组(20)可简记为矩阵形式

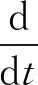
(23)

以上方程组的解可表示为

(24)

其中

T=exp(Wτ)

式中τ——时间步长W——常数矩阵

T——指数函数wn1,n2——常数矩阵

由此，问题可归结为矩阵T的计算，而矩阵T可通过精细积分方法[4]精确求得。

3 蝗虫切片图像降噪实验

3.1 蝗虫切片显微图像的获取

根据项目任务和目标要求，筛选满足条件的蝗虫直接作超薄连续切片，以获取蝗虫与微生物农药在组织水平上相互作用的图像，为在组织水平上的三维重建提供数据。显微镜下观察到的原始图像稍显模糊。在显微镜上观察得到的图像噪声属于混合噪声，成分复杂且含量不明确。为了便于量化对比各种方法，借助于PS软件采用人工方法对原始图像进行降噪和增强，结果如图2a所示。定量添加人工噪声(如高斯噪声、椒盐噪声等)后，如图2b所示。不同方法对图像的降噪效果如图2c～2e所示。

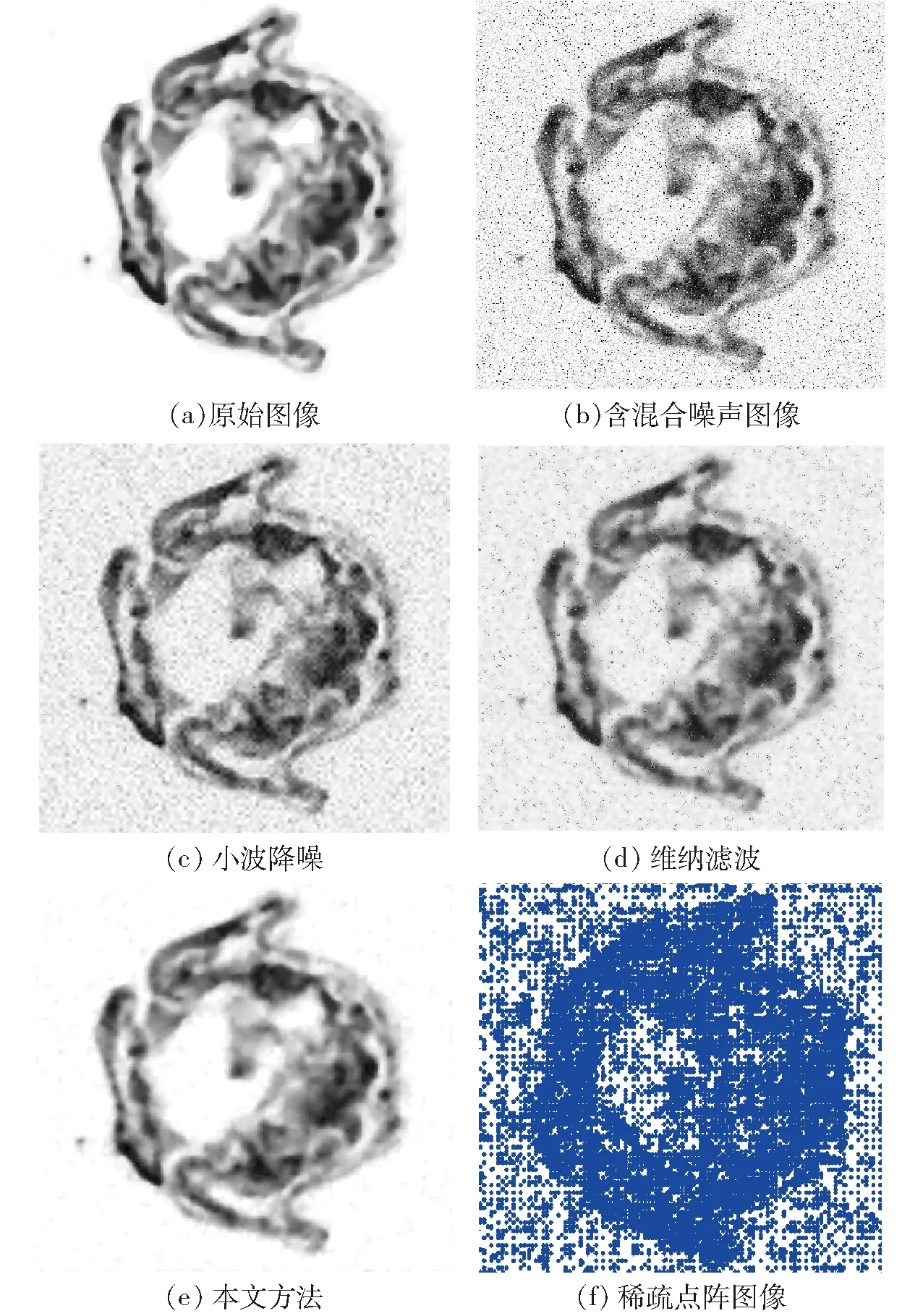
图2 含人工混合噪声图像的降噪效果对比Fig.2 Comparison of different denoising methods on slice image of locust with mixed noises

3.2 蝗虫切片显微图像降噪效果对比

3.2.1降噪方法对比

可用于生物图像降噪的典型方法包括维纳滤波、小波降噪、偏微分方程方法(变分法)、剪切波变换等。均值算子和中值算子也是图像降噪的常见方法，但适用范围较窄，不适合多种类型噪声混杂的情况。变分法[18-19]通过迭代求解偏微分方程实现图像降噪，且容易将细小纹理当作噪声处理[20]，尽管提高偏微分方程的阶数可以改善降噪效果，但迭代求解效率较低，精度也相应下降。因此，本节重点对比维纳滤波方法和小波降噪方法。维纳滤波是一种自适应滤波器，具有较广的适用范围和较好的降噪效果[21-22]。在众多的小波中，Daubechies小波是唯一同时具有正交性、光滑连续性、紧支撑性的小波；Symlets小波是在Daubechies小波的基础改进得到的[23]，保留了Daubechies小波的优点，且具有近似对称的特性，相对于Daubechies小波，具有更好的图像处理效果[24]。

本节用于对比实验的小波为sym4小波，采用Matlab内嵌函数wdencmp进行图像降噪，对应的阈值、逼近系数等参数由Matlab内嵌函数 ddencmp根据被处理图像自适应获取。维纳滤波方法则采用Matlab内嵌函数 wiener2来实现。图2d是序列切片图像的维纳滤波结果，估算局部图像噪声均值和方差的邻域图块的尺寸为6像素×6像素；图2c是通过小波变换实现图像降噪的结果。本文方法则采用Shannon-Cosine小波构造多尺度插值算子，N取23.123 447 719 961 405，此时精度具有更好的数值性能，Shannon-Cosine小波具有紧凑的支持域，提高了数值精度和效率[25]。输入图像后，对图像用P-M模型展开，用Shannon-Cosine小波配置法将偏微分方程离散成常微分方程，在此过程中，小波配置法对纹理实现自动捕捉，即根据图像灰度的变化特点自适应离散，以自适应选取图像的特征点。而后，小波精细积分法求解常微分方程得到高精度解，方程组的解即为降噪后图像在该点处的像素值。对切片图像进行降噪的效果如图2e所示，对应的稀疏点阵图像如图2f所示。

由稀疏点阵图可见，在图像纹理丰富区域，小波插值算子在纹理密集处特征点自动加密，特征点在平滑区域则自动减少。由此可见小波插值算子对图像中的纹理和轮廓具有较强的敏感性。其中，总像素点数为198 338，特征像素点为16 357个。稀疏点的个数只占图像像素总数的10%左右，利用稀疏点阵重构图像时，可有效消除噪声，同时保持较为清晰的纹理。单纯从视觉效果来看，本文方法优于小波降噪和维纳滤波，维纳滤波又优于symlets小波降噪。

3.2.2噪声种类对降噪效果的影响

为便于量化对比，对不含噪声的图像增加人工混合噪声(强度为0.05的椒盐噪声和均值与方差分别为0、0.02的高斯噪声)，结果如图2b所示。表1给出了采用不同方法得到的降噪图像的峰值信噪比(Peak signal-to-noise ratio，PSNR)和结构相似度(Structural similarity index, SSIM)。这两个参数是评价图像降噪方法的常用指标，此处直接采用Matlab中的内嵌函数psnr和ssim计算得到。

中值滤波对椒盐噪声具有非常强的敏感性，表1所示数值也反映了该点。而对混合噪声和高斯噪声来说，本文方法的降噪效果最好，明显优于其他方法。

3.2.3噪声含量对降噪效果的影响

通常，随着高斯噪声基本偏差的增大，噪声含量也相应增加。表2给出了在噪声含量增加时，不同滤波方法的去噪效果。可以看出，各种降噪方法中，峰值信噪比(PSNR)和结构相似度(SSIM)两个参数都随着噪声含量的增加而衰减，但本文方法始终具有最好的降噪效果。图3为不同降噪方法的降噪效果指标(PSNR和SSIM)随高斯噪声方差的变化曲线。随着高斯噪声方差由0.02增加到0.10，本文方法得到的降噪图像的PSNR下降了11.67%；而维纳滤波、小波方法、中值滤波和均值滤波方法得到的降噪图像的PSNR分别下降了25.36%、25.74%、17.96%、24.55%；上述5种方法的SSIM分别下降了13.67%、31.26%、33.85%、27.66%、22.78%。显然，本文方法随着噪声含量的增加，降噪效果参数衰减率最低，表明本文方法具有较好的鲁棒性和对不同图像较强的适应能力。

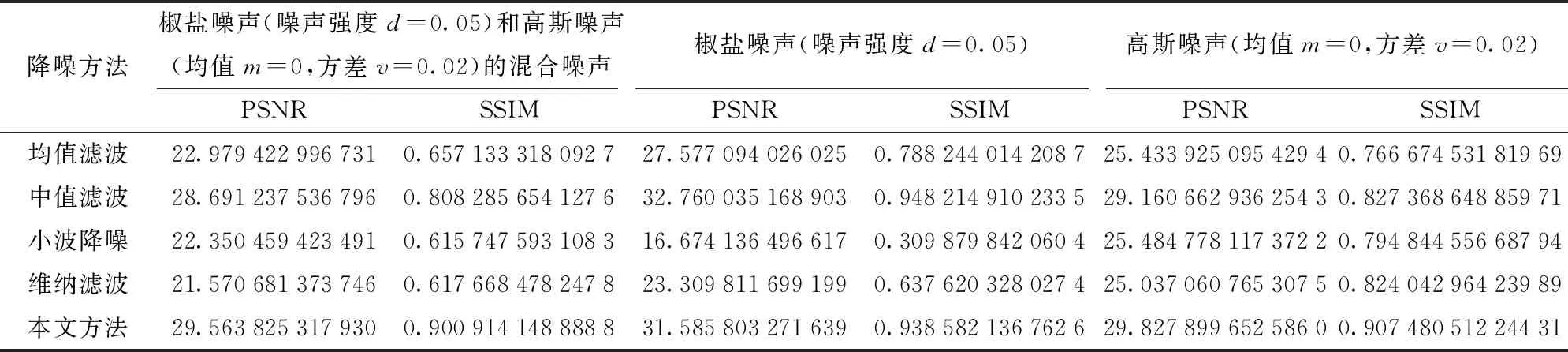
表1 噪声种类对降噪效果的影响Tab.1 Influence of noises type on denoising effect

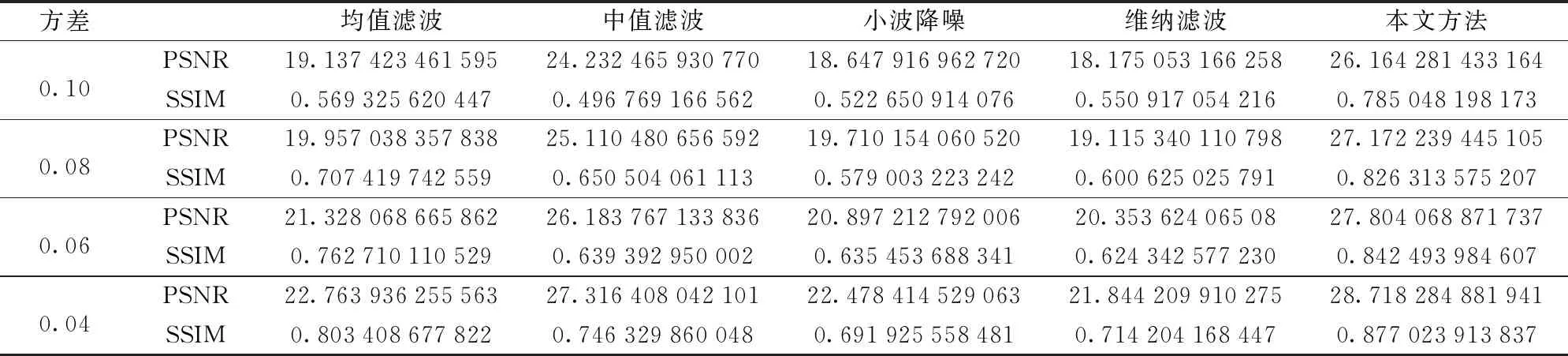
表2 高斯噪声方差对降噪效果的影响(均值m=0)Tab.2 Influence of Gaussian noise variance on denoising effect (mean m=0)

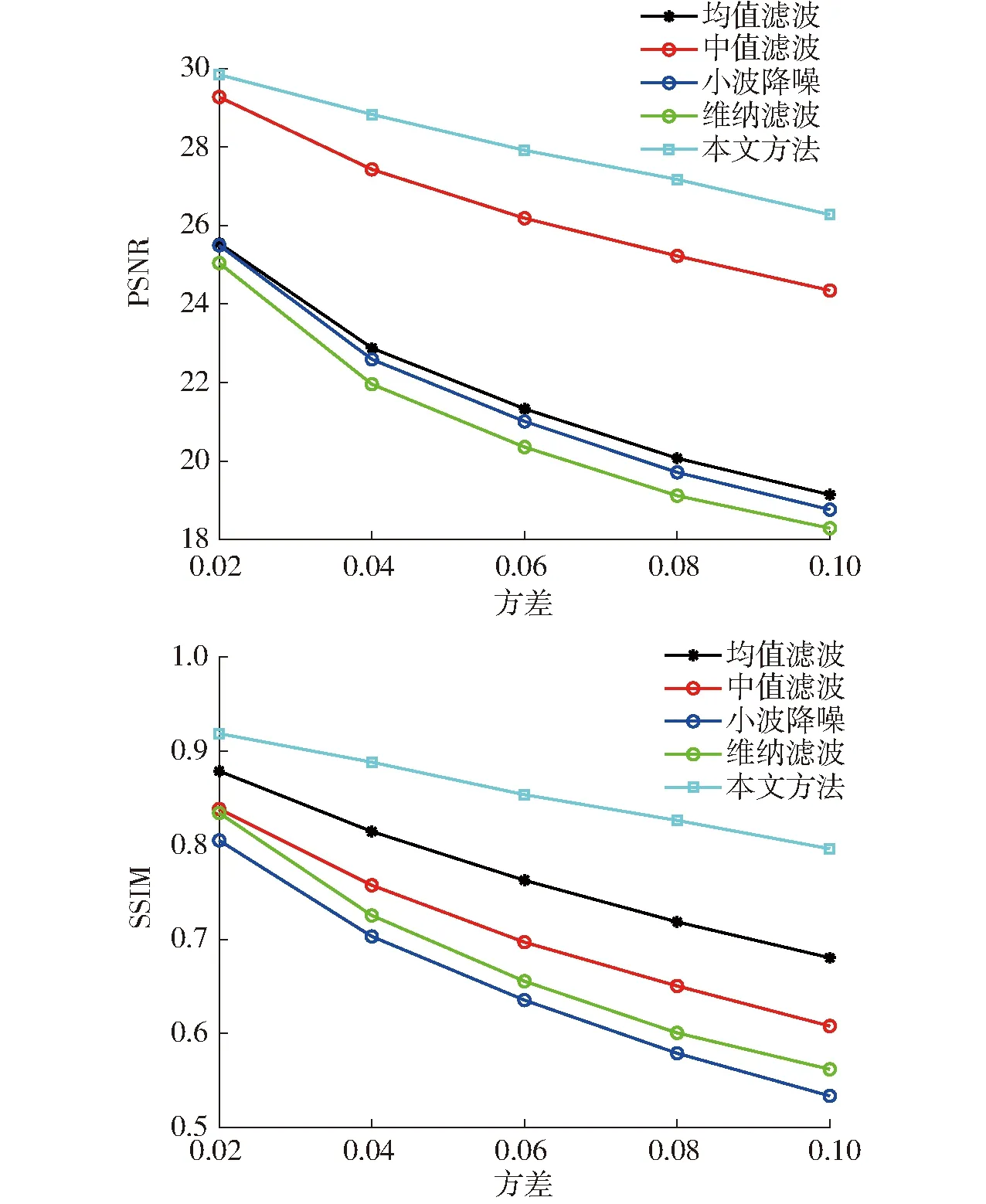
图3 峰值信噪比和结构相似度随高斯噪声方差的变化曲线Fig.3 Changes of PSNR and SSIM with increase of Gaussian noises variance

4 结论

(1)基于Shannon-Cosine小波构造的多尺度插值算子对蝗虫切片图像中的纹理和轮廓具有较强的敏感性，由此得到图像的稀疏特征点，为图像保纹理降噪奠定了基础。

(2)多尺度插值算子适合对包含混合噪声的蝗虫切片显微图像进行降噪，且对噪声含量不敏感，实验表明，本文方法随着高斯噪声方差由0.02增加到0.10，降噪图像的PSNR下降了11.67%，远低于其他方法。

(3)基于差分求解的变分法是生物图像领域的经典方法，基于该方法，本文采用了多尺度稀疏表示方法，从而具有较高的求解效率。