基于非线性模型预测控制的移动机器人实时路径跟踪

白国星 刘 丽 孟 宇 刘思言 刘 立 罗维东

(1.北京科技大学机械工程学院， 北京 100083; 2.吉林省农业机械研究院， 长春 130021)

0 引言

路径跟踪是车辆、机器人等移动装备自主行驶控制的一项核心技术，其任务是减小移动装备与参考路径之间的误差，从而使移动装备沿参考路径行驶[1]。路径跟踪控制的本质是一个多约束条件下的优化问题。模型预测控制(Model predictive control, MPC)能够显式地考虑系统约束条件[2-3]，因此被广泛应用于路径跟踪控制。目前，基于MPC的路径跟踪控制面临的较为突出的就是实时性问题[4]。

在一些路径跟踪控制研究[5-9]中，MPC的实时性问题尚未受到重视。不过这一问题得到了越来越多的关注，出现了较多的研究成果。文献[10]使用自动控制和动态优化工具包(Toolkit for automatic control and dynamic optimization, ACADO Toolkit)在计算机代码层面对控制器进行了优化。文献[11]则通过连续/广义最小残差(Continuation/Generalized minimal residual, C/GMRES)算法提高了控制器的求解效率。这两种优化方法对于提高控制器的实时性具有十分积极的意义，但与MPC本身的实时性能并不相关。

从MPC的角度出发，常见的实时性优化方案是线性化预测模型。文献[12]将这种方法命名为线性模型预测控制(Linear model predictive control, LMPC)，并证明LMPC相比非线性模型预测控制(Nonlinear model predictive control, NMPC)具有更好的实时性。文献[13-14]的研究重点并非实时性，但是也采用该方案设计了路径跟踪控制器，并命名为线性时变模型预测控制(Linear time-varying model predictive control, LTV-MPC)。此外，文献[15-23]的研究重点各不相同，但采用的控制方法都是LTV-MPC。

然而，线性化后的预测模型无法精确预测机器人的位姿状态，只能通过当前的误差进行预测，因此削弱了控制器对路径曲率突变和航向突变的响应能力[24-26]。对于农用机器人的路径跟踪控制，参考路径通常由直线和圆弧组成，其曲率变化很大，线性化预测模型的实时性优化方案并不十分适用。本文根据NMPC的控制周期、控制步数和计算复杂度之间的关系，提出两种实时性优化方案，并通过Matlab/Simulink中的Desktop Real Time实时性仿真框架以及实验验证，将这两种方案与线性化预测模型的方案进行对比研究。

1 NMPC控制器

在基于MPC的路径跟踪控制中，运动学模型的应用十分广泛[6,7-9,12-14,18-21]。在这种模型中，通常假设系统符合非完整约束，车体无侧向滑动。由于农用机器人速度较低，在转向时受离心加速度等侧向加速度的影响较小，所以可以通过机器人的运动学模型推导控制器的预测模型。

农用机器人的运动学模型十分成熟，其一般形式为

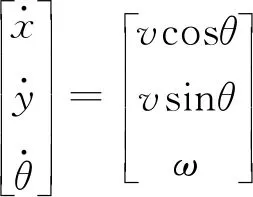
(1)

式中x、y——机器人转动中心的横、纵坐标，m

θ——机器人航向角，rad

ω——机器人航向角速度，rad/s

v——机器人纵向速度，m/s

为了便于表达，式(1)抽象为

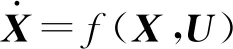
(2)

其中

(3)

参照文献[12-13]，采用欧拉法(Euler method)将式(3)离散化

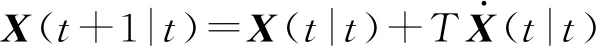
(4)

式中T——控制器的控制周期

将式(2)代入式(4)可得

X(t+1|t)=X(t|t)+Tf(X(t|t),U(t|t))

(5)

假设预测步数为Np，控制步数为Nc，则在预测时域内机器人的位姿状态为

(6)

设路径规划系统给出的参考路径点序列为Xref(t+i|t)(i=1,2,…,Np)。则优化目标函数可设计为

(7)

式中Q——误差惩罚项权重矩阵

R——控制量增量惩罚项权重矩阵

其中控制量增量惩罚项的作用是保证控制器较为平稳地控制机器人跟踪参考路径，避免机器人在短时间内过于频繁地加减速和转向。

路径跟踪控制即等效于在约束条件下求解

(8)

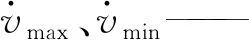
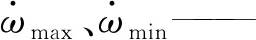
求解后，即可获得路径跟踪控制的输入变量序列

U*=(U(1),U(2),…,U(Nc))T

(9)

其中第1个元素U(1)即控制器在下一时刻输出的控制变量。

2 实时性优化方案

由于NMPC控制器每经过一个控制周期输出一组控制变量，所以求解式(8)的时间如果大于控制周期长度，则控制器的实时性就无法得到保证。因此较为容易得到的实时性优化方案为减少求解式(8)的计算复杂度。

由式(6)可知，机器人未来的状态，可以通过当前的状态和未来的控制输入预测获得，而对于每一步预测，理论上的最大搜索次数由约束条件决定。

(10)

式中ns——单步预测中的理论最大搜索次数

p——搜索步长

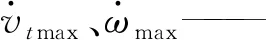
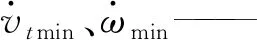
对于Nc步之后的预测，因为其控制变量与第Nc步相同，所以理论上NMPC控制器的预测时域内最大搜索次数为

(11)

由式(11)可知，减少控制步数可以大幅减少预测时域内理论最大搜索次数，因此可以提出如下实时性优化方案：

(1)方案1：减少控制步数方案。设置控制步数Nc1为1，并对与控制步数有关联的预测步数Np1进行相应调节，其他参数与NMPC控制器一致。

(2)方案2：降低控制频率方案。由于

(12)

式中Tc——控制时域

所以如果控制时域不变，增大控制周期，降低控制频率，尽管会增大单步预测中的理论最大搜索次数，但是可以减少控制步数，从而减少预测时域内理论最大搜索次数。在方案2中，设置控制周期T2=5T，预测步数Np2=Np/5，控制步数Nc2=Nc/5，其他参数与NMPC控制器一致。

3 仿真验证

本文提出的NMPC路径跟踪控制器实时性优化方案通过Matlab/Simulink中的Desktop Real-Time平台进行仿真验证，硬件中处理器为Intel®CoreTMi5-8500，内存为8 GB。仿真中各控制器的参数如表1所示，这些参数是通过参数调整获得的各控制器性能较佳时的取值。

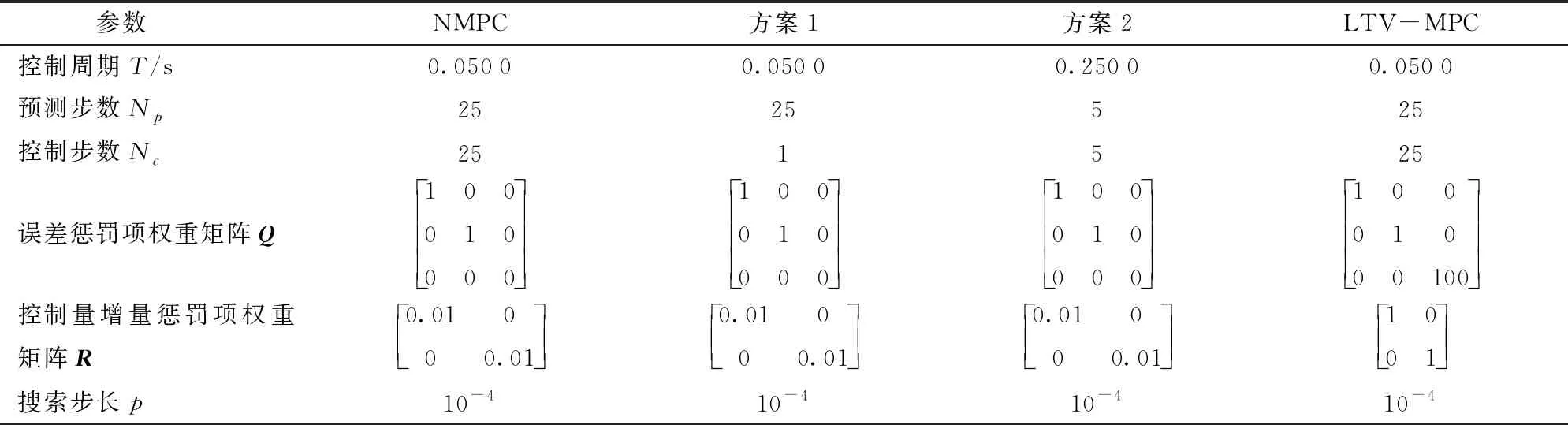
表1 机器人及NMPC控制器的参数Tab.1 Parameters of robot and NMPC controller

在仿真中，机器人的行驶速度设置为3 m/s，参考路径由直线和圆弧路段组成，其中圆弧路段的半径为10 m。

由图1可知，在较大的尺度范围内，所有基于MPC的路径跟踪控制器都可以实现路径跟踪，通过图2可以看出，NMPC控制下机器人的行驶轨迹偏离参考路径最少，本文提出的实时性优化后的控制器在精度方面稍逊色于NMPC控制器，而常见的LTV-MPC控制器则在面临参考路径曲率突变时出现了较大的误差。

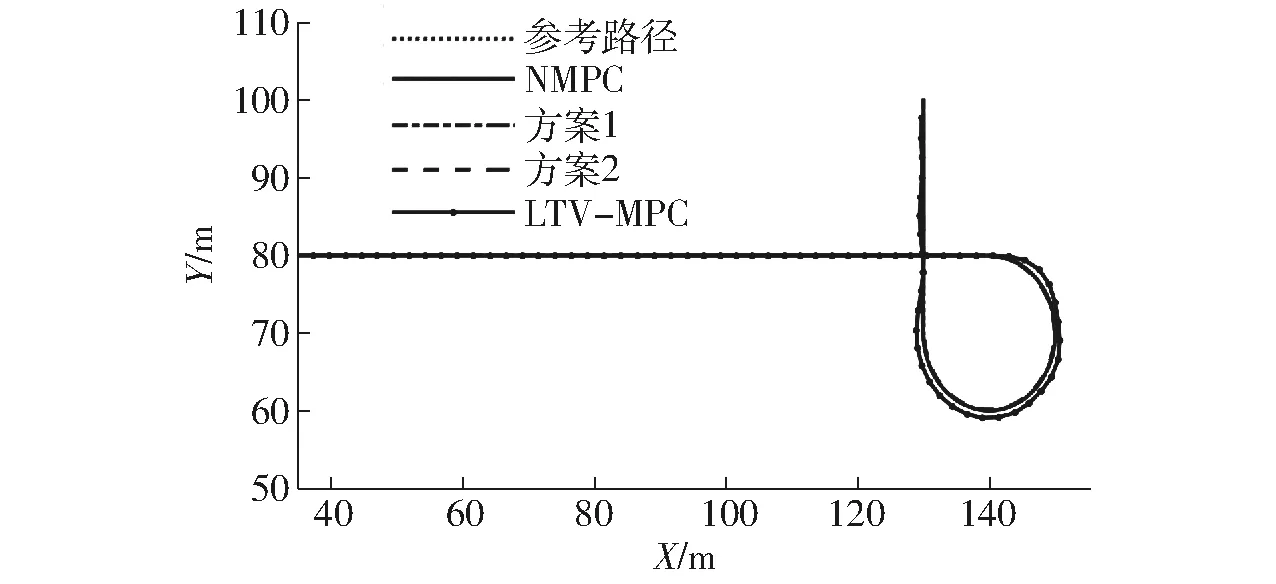
图1 仿真行驶轨迹Fig.1 Trajectory of simulation

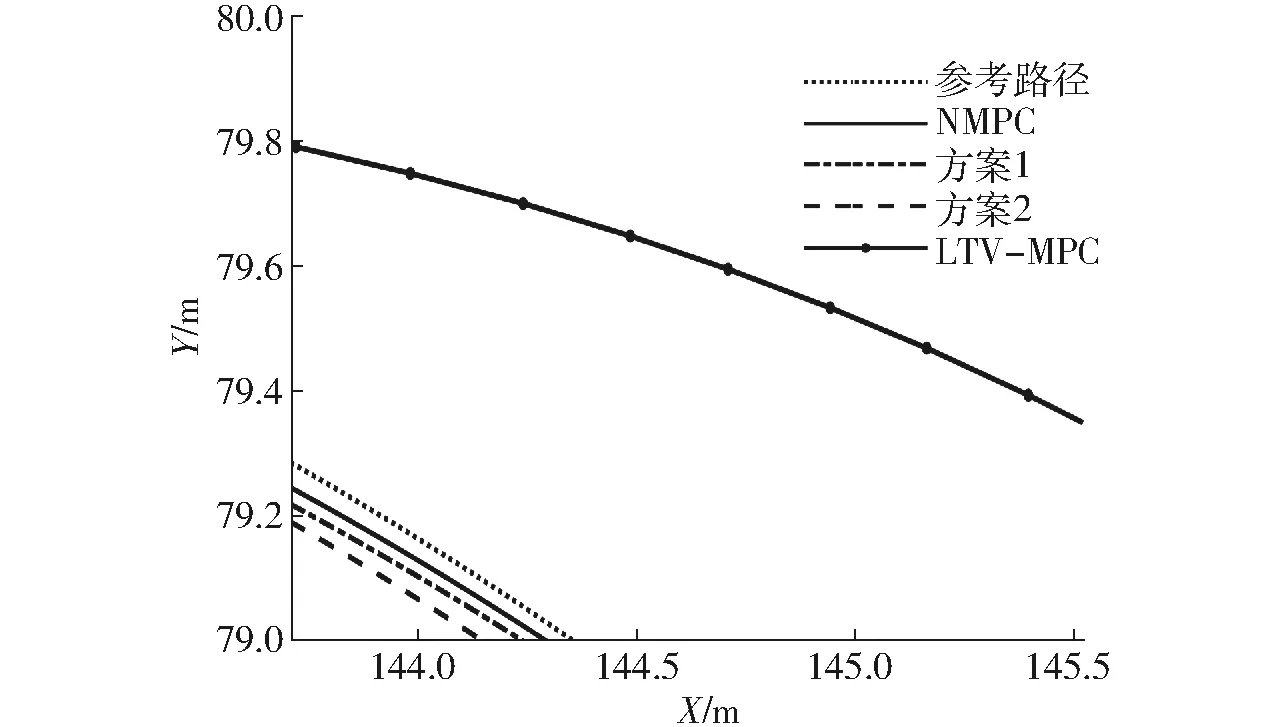
图2 仿真行驶轨迹的局部放大图Fig.2 Partial enlarged view of trajectory of simulation

图3中显示的横向误差即机器人距离参考路径的最短直线距离。NMPC、方案1、方案2和LTV-MPC的最大横向误差分别为0.081 1、0.094 7、0.107 4、1.167 4 m。由此可知，相比将预测模型线性化，在NMPC控制器的基础上进行实时性优化，可以较大程度地减少控制精度的下降。

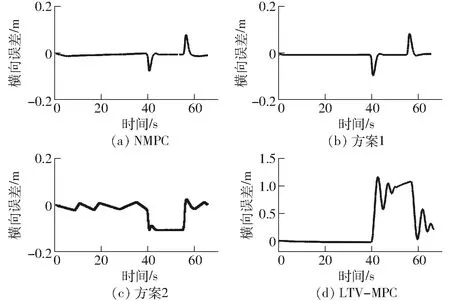
图3 横向误差仿真结果Fig.3 Displacement error of simulation

图4中显示的航向误差即机器人行驶方向与参考路径切线方向的偏差。NMPC、方案1、方案2和LTV-MPC的最大航向误差分别为0.054 6、0.060 8、0.058 2、0.210 6 rad。在NMPC控制器的基础上进行实时性优化，也可以较大程度地保证机器人的航向与参考路径一致。

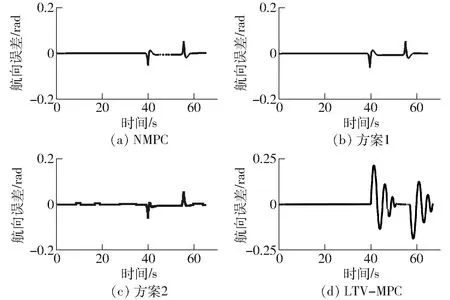
图4 航向误差仿真结果Fig.4 Heading error of simulation

图5显示的是每一控制周期内控制器的解算时间，由图5a可知，当路径的航向发生较大程度的变化时，NMPC控制器的解算时间显著增大，其最大值为0.087 0 s，是控制周期的1.74倍，而且解算时间超过控制周期的时段是连续的，由此可知此时NMPC无法满足路径跟踪控制的实时性要求。由图5b、5d可知，本文提出的优化方案1和LTV-MPC控制器的解算时间较短，其最大值分别为0.036 0、0.010 0 s，均远小于控制周期。本文提出的优化方案2则没有大幅度减少解算时间，其最大值为0.045 0 s，但是由于控制频率降低，在该仿真系统中控制周期为0.250 0 s，所以解算时间远小于控制周期，可以满足实时性需求。

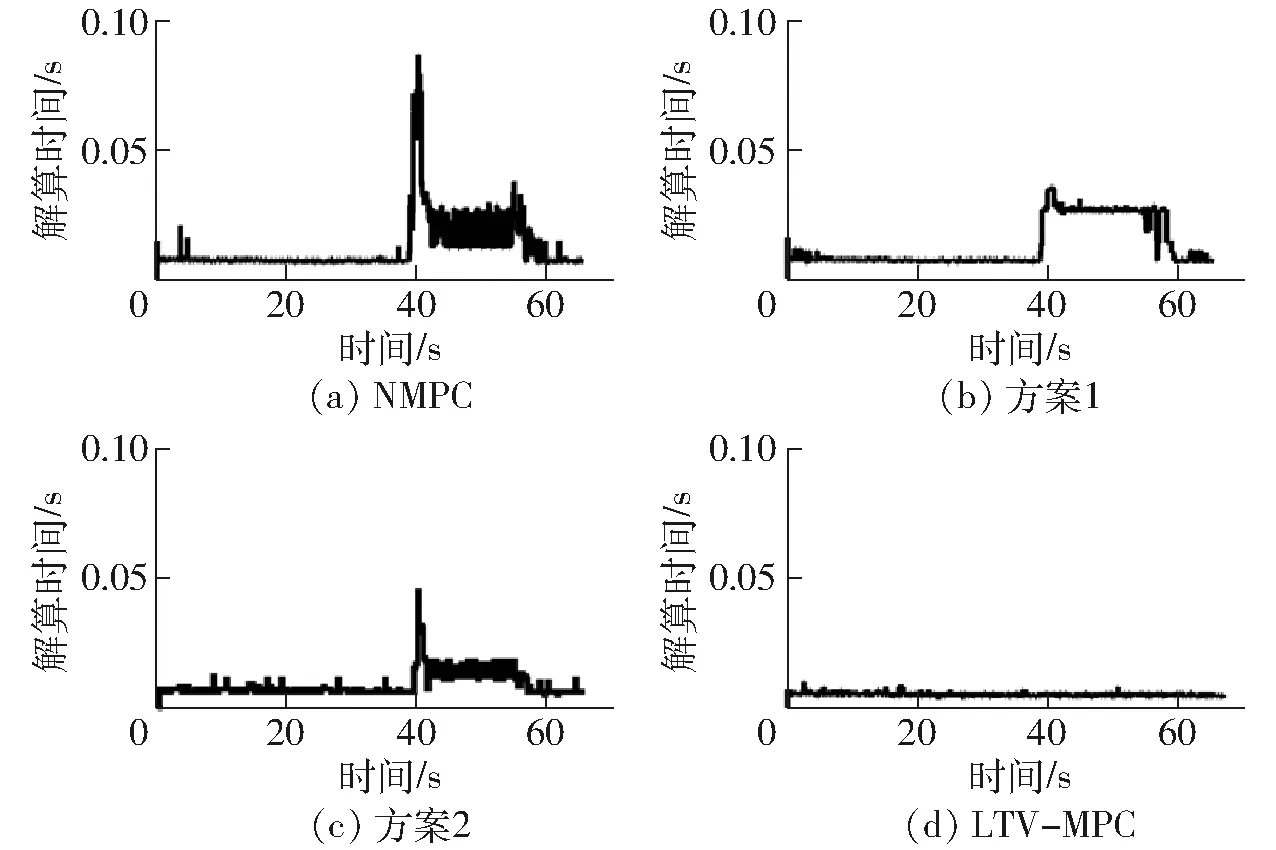
图5 仿真解算时间Fig.5 Computation time of simulation

4 实验验证

采用图6所示的国兴智能履带式机器人作为实验平台。实验系统的主控制器为研华ARK-3500型工控机，其处理器型号为Intel Core i5-3610ME，频率为2.7 GHz。执行控制器采用的是样机自带的线控驱动系统，用于实现行驶速度和航向角速度的控制。定位系统采用的是较为可靠的多传感器联合定位系统Inertial Labs INS-D，在RTK(Real time kinematic)模式下，该系统的坐标误差为0.01 m以内，航向误差为0.03°以内。图7所示为导航系统的回环检测结果。回环检测即人工操作机器人，使其移动一定距离后再返回原点，然后将其初始定位结果与最终定位结果之间的偏差作为定位是否可靠的判断标准。如图7所示，移动距离较短时，定位系统的累积误差较小，基本可以忽略不计。

图6 农用机器人模型样机Fig.6 Model prototype of agricultural robots

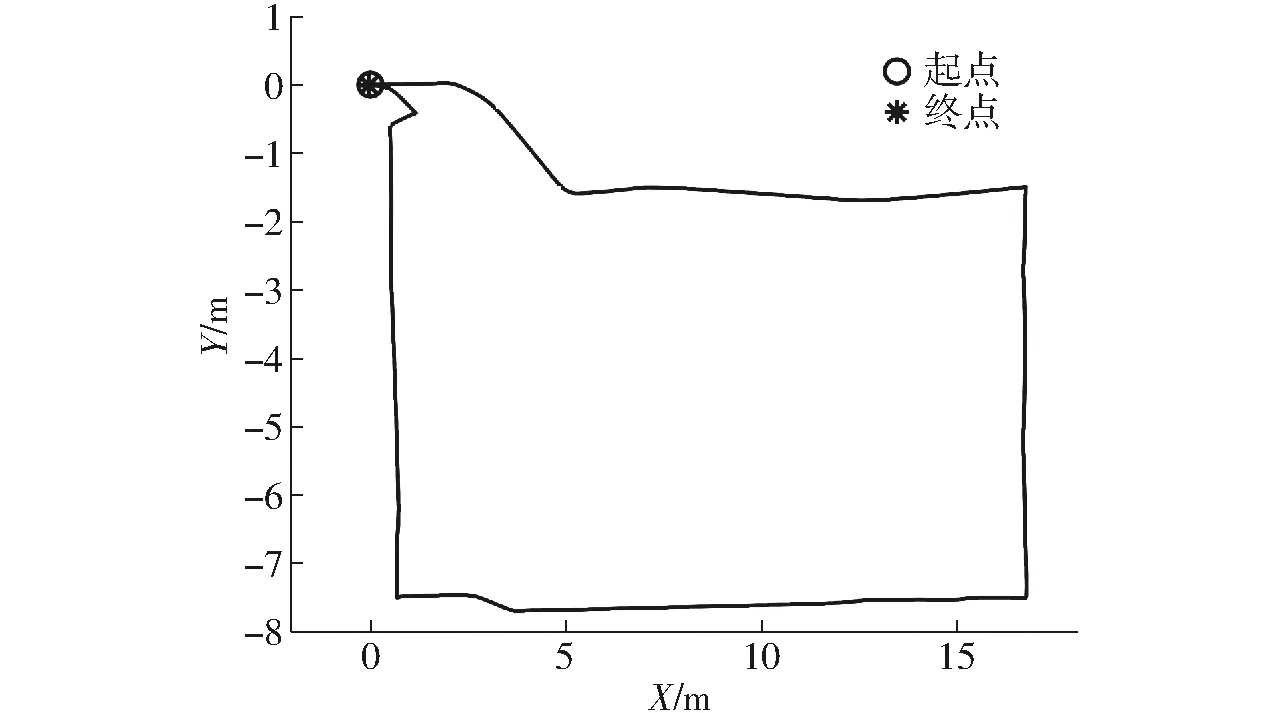
图7 定位系统回环检测结果Fig.7 Loop detection of positioning system

由于未经优化的NMPC控制器无法在控制周期内完成优化求解，所以不能用于实验验证。实验中对比了方案1、方案2和LTV-MPC，各控制器的参数与仿真中控制器的参数相同。由于实验场地面积有限，参考路径的弯道半径设置为5 m。为了在此情况下保证实验的安全性，机器人的行驶速度设置为1 m/s。

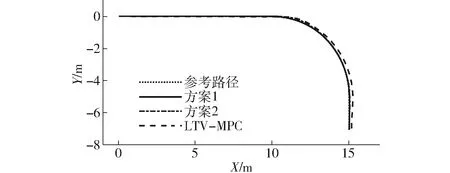
图8 实验行驶轨迹Fig.8 Trajectory of experiment

由图8可知，3种经过实时性优化的MPC控制器均可以控制机器人跟踪参考路径。图9显示了方案1、方案2和LTV-MPC的最大横向误差分别为0.019 9、0.075 6、0.238 1 m。图10显示了方案1、方案2和LTV-MPC的最大航向误差分别为0.032 3、0.071 3、0.118 9 rad。

图11显示了每一控制周期内控制器的解算时间，方案1、方案2和LTV-MPC的最大解算时间分别为0.047 0、0.187 0、0.010 0 s。

整体而言，实验结果与仿真结果具有一致的规律，采用减少控制步数或者降低控制频率的方案，可以实现对NMPC控制器的实时性优化。从控制精度来看，减少控制步数的效果相对较好。

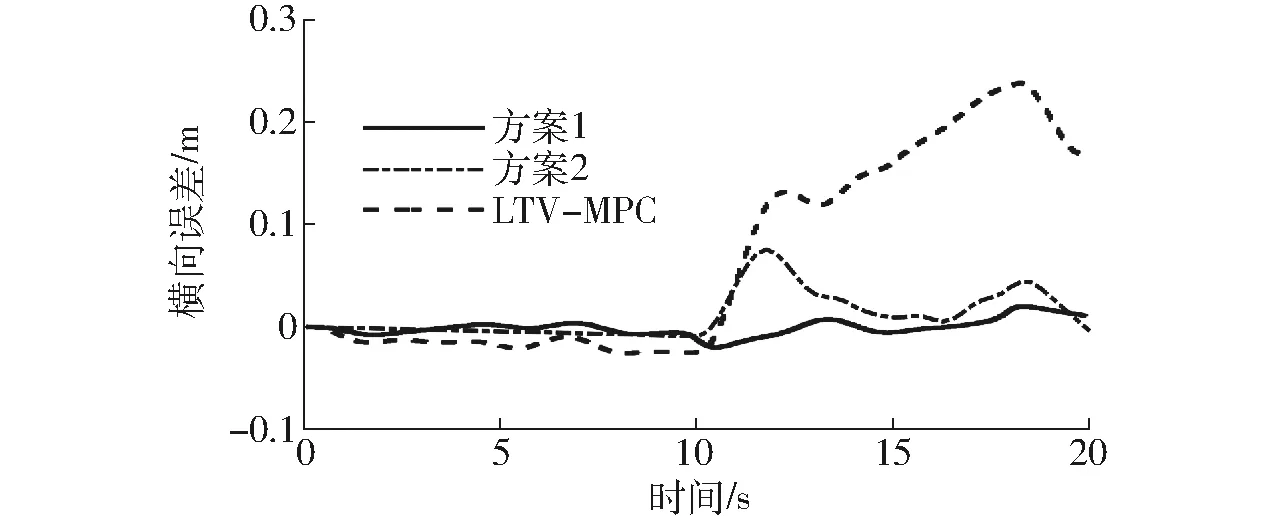
图9 实验横向误差Fig.9 Displacement error of experiment

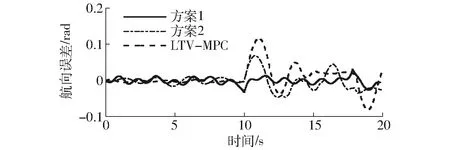
图10 实验航向误差Fig.10 Heading error of experiment

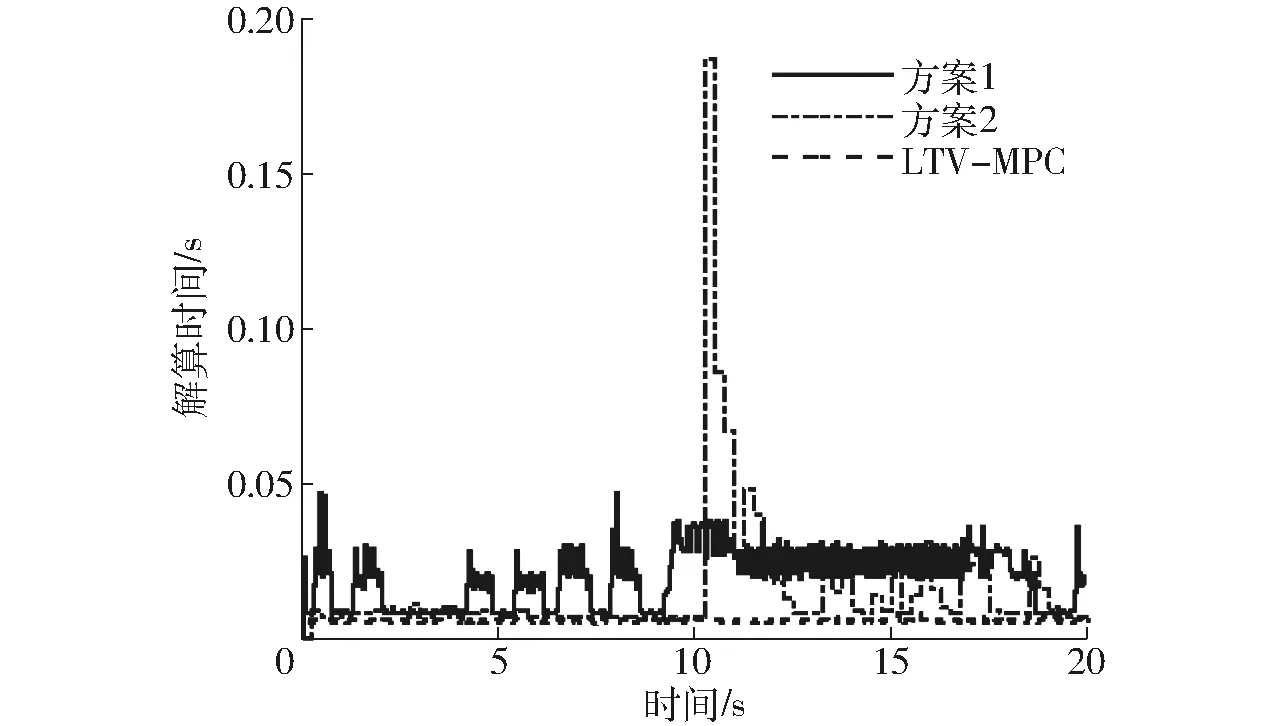
图11 实验解算时间Fig.11 Computation time of experiment

5 结论

(1)针对基于NMPC的机器人路径跟踪控制的实时性问题，基于模型预测控制算法提出了两种实时性优化方案，即减少控制步数方案和降低控制频率方案。对经过实时性优化的NMPC控制器与未经优化的控制器以及经过预测模型线性化的控制器进行了对比。

(2)仿真与实验结果表明，未经优化的NMPC控制器在实时性方面表现不佳，仿真中NMPC控制器在控制周期内的最大解算时间大于控制周期，无法满足实时性需求；采用减少控制步数方案对NMPC控制器进行优化后，仿真和实验中的最大解算时间均小于控制周期，能够满足实时性需求，路径跟踪的控制精度较高；采用降低控制频率方案对NMPC控制器进行优化后，仿真和实验中的最大解算时间均小于控制周期，能够满足实时性需求，但控制系统的误差稍大于采用减少控制步数方案时的误差；采用线性化预测模型方案，即将NMPC控制器转变为LTV-MPC控制器后，控制器实时性大幅度提高，但在跟踪曲率变化较快的参考路径时，LTV-MPC控制器的精度较差。

(3)考虑到农用机器人的工作场景，控制器除了要保证实时性，还需保证机器人的灵活性，即机器人跟踪曲率变化较快的参考路径的能力，因此，减少控制步数是较佳的实时性优化方案。在实际工程应用中，也可以将减少控制步数方案与降低控制频率方案组合使用，进一步保证NMPC路径跟踪控制器的实时性。