基于逻辑自映射和Beta 变异的混沌蚁狮优化算法∗

胡元娇 郭玉纯

(西安邮电大学计算机学院 西安 710121)

1 引言

蚁狮优化算法（antlion optimizer，ALO）［1］是由澳大利亚学者Seyedali 于2015 年提出的一种新的仿生智能优化算法。相比其他智能方法，例如粒子群算法［2］、蝙蝠算法［3］和人工蜂群算法［4］，ALO 算法具有调节参数少，易于实现、求解精度高等优点。目前，ALO算法已经被广泛使用，例如：特征选择［5～6］，多目标优化［7～8］，优化SVM 参数［9］，解决最优潮流问题［10］，硅单晶热场温度模型的参数辨识［11］，无人机的航迹规划问题［12］，以及其他一些工程领域［13］。但是，在应用中蚁狮优化算法也存在易陷入局部最优、后期收敛速度较慢、出现早熟收敛的问题。为了克服蚁狮优化算法的缺点，本文提出了一种基于逻辑自映射和Beta 变异的混沌蚁狮优化算法（chaotic antlion optimizer，CALO）。通过对5 个Benchmark 基准函数的寻优测试表明，CALO 算法与ALO算法和PSO 算法相比，其全局搜索能力更强、收敛速度更快、精度更高、寻优能力更佳。

2 基本蚁狮优化算法

2.1 ALO算法的数学模型

式中：cumsum 表示计算蚂蚁游走位置累加函数，n表示最大迭代次数，t 表示游走步长，r(t)是一个随机函数，其表达式如下：

式中：rand 为［0，1］上均匀分布的随机数。

为了使蚂蚁在可行域范围内随机游走，根据式（3）进行归一化：

式中：ai表示第i 维变量随机游走的最小值；bi表示第i 维变量随机游走的最大值；表示在第t 次迭代第i 维变量的最小值；表示在第t 次迭代第i 维变量的最大值。

蚂蚁游走的区域边界受蚁狮位置的影响：

式中：ct表示第t 次迭代所有变量中的最小值；dt表示第t 次迭代所有变量中的最大值；表示第t 次迭代通过轮盘赌选中的蚁狮或者精英蚁狮第j 个变量的位置。T 为最大迭代次数；t 为当前迭代次数；ω 为随迭代次数增大的数（ω=2，t＞0.1 T；ω=3，t＞0.5 T；ω=4，t＞0.75 T；ω=5，t＞0.9 T；ω=6，t＞0.95 T）。

当蚁狮捕获蚂蚁后，其位置更新到蚂蚁位置以增强其捕获猎物的机会：

式中：f 为适应度函数。

轮盘赌选择的蚁狮和精英影响着蚂蚁的随机游走：

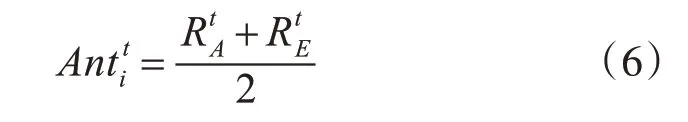
2.2 基本蚁狮优化算法的局限性

ALO 算法的寻优能力主要依赖于蚂蚁和蚁狮种群个体之间的相互作用和影响。蚂蚁绕选定的精英蚁狮进行随机游走实现对搜索空间的探索，如果选取当前精英个体在局部最优邻域内并不是全局最优值，则容易带领整个种群陷入局部最优，降低种群的多样性，同时适应度较差的种群个体会使得算法的收敛速度变慢，精度不高，甚至出现进化停滞现象。提高种群的多样性以加快收敛速度和精度可以提高蚁狮优化算法的性能。

3 改进蚁狮优化算法

3.1 混沌优化策略

本文采用逻辑自映射函数来产生混沌序列［14］，数学表达式为

混沌优化的过程如下。

1）在搜索过程中的某个时刻，蚂蚁i 位于D 维空间内，位置为xid。首先按照式（8）将个体空间位置的每一维映射到［-1，1］上：

式中：aid表示蚂蚁i 第d 维变量的上界，bid表示蚂蚁i 第d 维变量的下界。

2）将变换后的变量使用式（7）进行载波操作，将获得的新混沌变量序列按照式（9）变换到原解空间：

3）在此过程中，如果搜索到更优的解则更新原来蚂蚁的位置为当前更优位置；否则继续进行混沌搜索，当达到最大搜索次数时停止搜索。

3.2 Beta变异策略

Beta分布是一组定义在区间［0，1］上的连续概率分布，有两个形参α 和β，α 和β 都为正数，用于控制函数图像形状。Beta分布的概率密度函数是：

式中：Γ 是Gama 函数；B 是一个归一化常数，用于确保总概率和为1；x 是随机变量；当形状参数α和β 接近零值时，Beta 分布接近极限的伯努利分布。Beta变异能取得较好的扰动效果，且利于算法控制变异方向及位置边界。本文根据Beta 分布设计了一种精英定向Beta变异算子，用于每个迭代周期的变异，其目标是加快收敛速度，去除随机方向变异带来的不确定性，对目标个体进行变异时，变异方向指向精英个体。精英定向Beta 变异的位置变异公式如下所示：

式中：σ 为Beta 分布函数产生的随机值，σ∈[0,1]，xid为变异前的位置，x'id为变异后的位置，xelite为精英个体。由公式可以看出，变异后的点位于精英个体和变异个体之间，即变异后的个体向精英个体靠拢，σ 越小，离精英个体越近。

3.3 CALO算法描述

本文提出的CALO 算法引入逻辑自映射混沌序列［15］优化精英个体，使得精英个体摆脱局部极值的约束，向局部最优邻域内的全局最优点靠拢，从而提高种群多样性。使用Beta 变异策略［16］对适应度值较差的种群个体采取定向变异的方式，去除随机方向变异带来的不确定性，变异方向指向精英个体，加快了算法的收敛速度，提高算法的求解精度，使得种群在迭代过程中能保持持续优化的能力。具体算法如下。

Step1：初始化蚂蚁和蚁狮的数目、位置、最大迭代次数、最大搜索次数、适应度函数维数、变量范围的上界和下界。

Step2：计算蚁狮和蚂蚁个体适应度函数值，找到当前最好的蚁狮个体并作为当前精英个体。

Step3：更新蚂蚁的位置。

Step4：对所有种群的适应度值排序，取性能较好的前n 个种群个体采用混沌优化策略进行优化；对性能较差的后n 个种群个体采用Beta 变异策略产生新的个体。更新并保留精英蚁狮个体位置。

Step5：判断算法迭代终止条件是否满足，若满足则转至Step6，否则跳转至Step2～4。

Step6：输出个体最优值，算法结束。

4 实验设计及仿真分析

4.1 测试函数设计

为验证提出的CALO 算法的特性，本文选取了5 个Benchmark 基准函数对算法进行寻优测试，见表1所示。实验仿真环境Matlab R2017a。

4.2 实验条件设计

每个算法实验按照维度的不同划分为三组，分别是维度N=10、N=20、N=50，随着维度的增加，测试难度不断增大，更加能反映算法在不同维度下的搜索能力，体现出算法综合性能。每组实验在每个测试函数下都独立执行30 次，记录下30 次执行后的最优适应度值BF（Best Fitness）、平均最优适应度值MBF（Mean Best Fitness）、标准差SD（Standard Deviation）、平均适应度值误差AE（Average Error）这四组数据，其中AE 的计算公式为AE=MBF-BF。在实验设计中，三个算法的参数始终保持一致。具体设置如下：蚁狮和蚂蚁的种群数均为30个，最大迭代次数为1000次，混沌搜索次数为30次，搜索范围见表1 所示。PSO 参数设置如下：c1=2、c2=2、w=1.0。5 个基准测试函数进化曲线如图1所示，10维、20维和50维的测试结果见表2所示。

4.3 结果分析

根据图1所示在1000次迭代情况下，不同基准函数在不同维度下的进化曲线可以看出，ALO算法和PSO 算法均出现了早熟收敛及算法陷入局部最优解的问题，而此时CALO 算法可以保持较强的开发能力，收敛速度也比另外两种算法要快，种群多样性得以改善，算法可以成功跳出局部最优解搜索到全局最优解。

表1 基准测试函数

图1 5个基准测试函数进化曲线

表2 多组测试函数不同维度下的仿真结果

从表2 的仿真结果可知：无论是单峰函数还是多峰函数，根据最优适应度值和平均最优适应度值可以看出，本文提出的CALO 算法均优于另外两个算法，说明CALO 算法的平均寻优精度能力更强；根据标准差和平均适应度值误差可以看出，CALO算法相比其他两种算法均有较为满意的解，说明CALO算法的稳定性更好，性能更优越。

综上所述，在BF、MBF、SD、AE 四组指标下，可对三种算法的寻优性能排序如下：CALO＞ALO＞PSO。所以无论从算法精度层面考虑还是从稳定性层面考虑，CALO 算法具有更强的寻优能力和稳定性。

5 结语

本文在研究基本蚁狮算法的基础上，针对ALO算法在寻优过程中有可能会陷入局部最优，提出了一种基于逻辑自映射和Beta 变异的混沌蚁狮优化算法。该算法在ALO 算法中引入逻辑自映射混沌序列，丰富了蚂蚁个体的行为，并将蚂蚁个体均匀映射到定义空间中。使用Beta 变异策略对适应度值较差的种群个体进行变异，使得算法能有效跳出局部极值。对五个Benchmark 基准函数的寻优测试表明，CALO 算法与ALO 算法和PSO 算法相比，其寻优速率、收敛精度及算法稳定性更佳。