基于DBSCAN 的缺失值填充算法研究∗
冯宪凯 黄树成
(江苏科技大学计算机学院 镇江 212003)
1 引言
在数据挖掘领域,数据预处理扮演着非常重要的角色,数据质量好坏直接影响数据挖掘算法的正确性。对正确完整的数据进行数据挖掘可以得到宝贵而有价值的信息,进而让用户做出正确的决策[1]。而对错误的数据挖掘得到的信息必然是错误的,没有任何价值。由此可见正确完整的数据的重要性。但是数据集中难免会有各种各样的脏数据,主要包括重复记录、缺失值和错误数据。其中较关键的就是缺失值问题,导致缺失值记录的原因包括很多,例如数据采集错误,度量方法错误和人工的疏忽录入等。因为数据是宝贵的,要把缺失值记录变成宝贵的数据就要对其进行数据清洗。因此,如何处理缺失值记录已成为数据预处理领域研究的热门话题之一。
当前对于缺失值记录的处理办法通常包括两种,第一种方法就是删除法,即对缺失值记录直接从数据集中删除,虽然这可以保证剩余数据集结果的正确性,但也白白浪费了大量的数据资源,而且当数据集中存在大量的缺失值记录时,直接删除会影响数据集的完整性和后续数据挖掘结果的正确性。另外一种方法是基于填充技术的方法,即用合适的数据填充缺失值记录对应的属性。填充法无论是从量上还是质上都明显好于第一种方法。当前国内外已提出多种缺失值记录填充方法,主要包括分类方法、关联规则[12]和统计方法[13]等;虽然这些方法在不同的环境下都有各自的优点,但还是有一些不足。
本文研究聚类在缺失值填充中的应用[7]。聚类顾名思义是将相同的事物聚集到一起,而缺失值记录是和数据集有关联的,我们通过聚类将数据集分成几大类,然后分别比较缺失值记录和聚类分成的几大类的相似度,然后取其相似度最大的类标记缺失值记录,该缺失值记录的缺失属性值就可以用该类的所有记录的属性均值填充。基于DBSCAN的缺失值填充算法可以将缺失值记录和数据集中相似度最高的类进行关联,然后计算该类的属性均值来估计缺失值,处理后的缺失值记录具有较高的正确率。但是该算法仍有一些不足,主要因为传统的DBSCAN 算法使用固定的ε 邻域半径进行聚类,可以对密度均匀的数据集有很好的聚类效果,但却不能处理多密度数据集[2]。因此,本文提出一种改进的基于DBSCAN算法的缺失值填充算法:新算法提出可变的MinPts 邻域来代替固定的ε 邻域来进行核心对象的查找,可以根据记录周围的密度自适应调整邻域大小,还能过滤噪点;借助于有向图的强连通分量,可以让核心对象之间密度相连,避免了一个孤立点将两个不同的类连接成一个类的情况;在聚类完成后,计算缺失值记录与数据集中的多个类相似度时,利用欧几里得距离公式的三角不等式性质[5],减少了距离的计算量和比较次数,尤其在数据集数据量很大的情况下,能极大地提高算法的运行效率。
2 改进的基于DBSCAN 的缺失值填充算法
2.1 基于DBSCAN的缺失值填充算法
基于DBSCAN的缺失值填充算法思想:首先将数据集按照数据的完整性分成两个数据集,即完整数据集和缺失值数据集。完整的数据集保存了整个数据集的完整信息,因此,我们对完整的数据集进行聚类,得到若干个分类,然后再对缺失值数据集中的记录逐一的与这若干分类进行相似度比较,得到相似度最大的那个类标记缺失值记录,最后可以根据缺失值记录所属类的信息计算出缺失值并加以填充。
基于DBSCAN 算法的缺失值填充算法的流程如图1所示,详细步骤如下:
步骤如下:
输入:数据集D,参数Eps 和MinPts。
输出:对缺失值记录填充完成的完整数据集D′。
Step1:先将数据集D 根据样本属性的完整性划分成两部分,包括完整数据集C 和缺失值数据集M 。
Step2:对数据集C 进行DBSCAN 算法聚类,该算法将根据数据对象的密集程度将数据集划分为k 个类,记为C1,C2,…,Ck。
Step3:根据上面得到的k 个类,遍历数据集M 中的记录,遍历的同时,逐一比较缺失值记录与这k 个类的数据相似度,取相似度最大的那个类标记缺失值记录。
Step4:填充M 中的缺失值,根据上一步标记的所属类,对M 数据集中的每一条记录的缺失值用标记类的属性均值填充。

图1 基于DBSCAN算法的缺失值填充算法流程图
通过上面几个步骤,我们就将M 中的每一条记录缺失值填充完毕,填充过的数据集记为M',数据集M'和数据集C 就构成了完整数据集D',算法最后输出数据集D'。
从上面的算法步骤中,可以看出上面算法有两个不足,1)传统的DBSCAN 算法使用固定的ε 邻域半径进行聚类,可以对密度均匀的数据集有很好的聚类效果,但却不能处理多密度数据集,对于包含多个密度类的数据集,该算法的填充效果可能不太令人满意[2]。2)随着数据量的增加,该算法的时间复杂度也不断增长。
2.2 改进算法的策略
本文针对上面填充算法的不足,将从两个方面进行改进。
1)针对传统的DBSCAN 算法使用固定的ε 邻域半径进行聚类,可以对密度均匀的数据集有很好的聚类效果,但却不能处理多密度数据集,提出一种基于DBSCAN 的多密度聚类算法用于缺失值填充。
定义1:(MinPts 邻域)数据集合D 中数据对象a 的MinPts 邻域是指在其邻域半径ε 范围内距离数据对象a 最近的MinPts 个点的集合(包含点a),表示为NMinPts(a)。定义为NMinPts(a)={b∈D|dist(a,b)≤min(ε,dist(a,ak))}。ak表示离数据对象a 第MinPts 个最近的邻域点。
定义2:(核心对象[2])若数据对象a 满足|NMinPts(a)|=MinPts,那么数据对象a 就是核心对象。
定义3:(直接密度可达)对于数据集D,设数据对象b 在核心对象a 的MinPts邻域内,那么我们就说数据对象b 从核心对象a 出发是直接密度可达的。
定义4:(密度可达)对于数据集D,如果存在一条数据对象链a1,a2,…,an,设p=a1,q=an,ai∈D(1≤i≤n),ai+1从ai关于ε 和MinPts 直接密度可达的,那么数据对象p 是从数据对象q 关于ε和MinPts 密度可达的。
定义5:(密度相连)对于数据集D 中的两个数据对象a 和b,如果a 是从数据对象b 关于ε 和MinPts 直接密度可达的,并且b 是从数据对象a 关于ε 和MinPts 直接密度可达的,那么数据对象a和b 是关于ε 和MinPts 密度互联的,即有向图的强连通分量。
基于DBSCAN的改进算法步骤:
输入:数据集D,参数ε 和MinPts。
输出:含有类标记的结果数据集D'。
Step1:从数据集中随机找一个核心对象a,对该核心对象MinPts 邻域内的数据对象进行遍历,并标记为类C1,如果邻域内的数据对象b 和a 密度相连,那么就将核心对象b 加入到队列Q 中,否则数据对象b 是类C1的边界对象。
Step2:遍历队列Q,依次从队列Q 中取出一个核心对象,对该核心对象执行步骤1,直到队列Q 为空,那么类C1的所有数据对象聚类完成。
Step3:再从数据集D 中查找是否还有未标记的核心对象,如果找到了,就执行步骤1和步骤2,否则就将数据集D中还未标记类的数据对象标记为噪点。
传统的DBSCAN算法,需要用户自己输入邻域半径参数ε,如果邻域半径ε 过大,会将噪点划分到类中,识别不了噪点,也会将两个高密度的类划分到一类中。如果邻域半径ε 过小,数据距离过大的类就无法识别,并且会被标记为噪点,影响聚类质量。改进的算法提出了MinPts邻域的概念,借助于图的强连通分量,可以获得数据集中每个类的核心对象集合。该算法可以自适应的根据数据对象周围密度的大小自动调整邻域半径大小,解决了传统DBSCAN 在邻域半径参数ε 固定情况下,无法对多密度数据集进行聚类的问题,同时该改进算法也可以正确地识别噪点。
2)在使用基于DBSCAN的填充算法的时候,通过对完整数据集C 聚类,形成了k 个聚类,然后通过对缺失值数据集M 进行缺失值填充时候,需要计算数据集M 中每条数据对象与上面k 个聚类的相似度,在缺失值数据集M 数据量很大的时候,计算缺失值记录与类的相似度需要浪费很多的时间,由于计算相似度距离的时候,我们使用的是欧几里得距离公式,而欧式距离满足三角不等式性质,假设c1 和c2 是数据集的两个聚类中心,则对于任意一个数据对象b,会得到如下公式:

即两个聚类中心c1 和c2 的距离小于b 到c1距离与b 到c2 的距离之和。如果d(c1,c2)≥2d(b,c1),我们就可以得出结论d(b,c2)≥d(b,c1),即b 到c1 距离小于b 到c2 的距离,这样我们就可以不用计算d(b,c2),避免了一些不必要的计算与比较,提高了算法的运行效率。
2.3 改进的基于DBSCAN的缺失值填充算法步骤
基于DBSCAN 的缺失值改进填充算法步骤步骤如下:
输入:数据集D,参数Eps 和MinPts。
输出:对缺失值记录填充完成的完整数据集D'。
Step1:先将数据集D 根据样本属性的完整性划分成两部分,包括完整数据集C 和缺失值数据集M 。
Step2:对数据集C 进行改进的DBSCAN 算法聚类,该算法将根据数据对象的密集程度将数据集划分为k 个类,记为C1,C2,…,Ck。
Step3:借助于三角不等式定理,分别计算缺失值记录集M 中的记录和上面得到的k 个类的相似度,选出相似度最大的那个类,将缺失值记录赋给该类。
Step4:填充M 中的缺失值,根据上一步标记的所属类,对M 数据集中的每一条记录的缺失值用标记类的属性均值填充。
3 实验结果
本实验使用的数据集来自UCI 网站的Banknote Authentication Dataset,该数据集包含1372 条数据,由于数据集是完整的不包含缺失值的数据集,我们采用人工的方式对其中100 条记录的相应属性清除,然后重新放在数据集中,然后通过对传统的DBSCAN缺失值填充算法、均值填充算法和本文提出的改进的基于DBSCAN 的缺失值填充算法算法进行实验对比,主要从算法结果的正确率进行比较,即正确填充的缺失值记录的数量占总缺失值记录数的比率。设定P 是缺失值填充的正确率,M 是正确填充的缺失值记录的数量,N 是缺失值记录总数,那么可得正确率公式:

当p=0 时,表示算法没有正确填充任何一条缺失值记录,如果p=1,则表示所有的缺失值记录都被正确的填充。
下面我们通过实验来比较一下三种算法在缺失值记录填充正确率方面的差异。
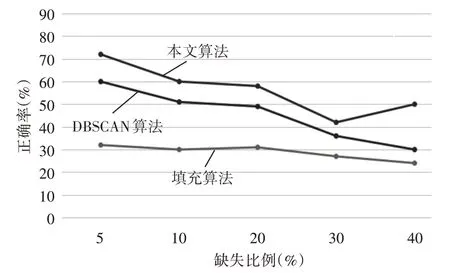
图2 不同填充算法在不同缺失比例下的正确率折线图
从图2 中我们可以看出,在数据对象的缺失值较少的情况下,本文算法和DBSCAN填充算法正确率都很高,随着确实比例的增大,填充算法的正确率都有所下降,当缺失比列很大时,算法的正确率就会变得很低。

表1 不同填充算法最优正确率对比表
从上面表格中可以看出,使用基于DBSCAN的缺失值填充算法的正确率明显高于均值填充算法的正确率,因为均值填充算法使用的是整个数据集的属性平均值填充缺失值,完全忽略了数据集中记录的差异性,所以填充的正确率明显很低。而基于DBSCAN 的缺失值填充算法通过对完整的数据集进行聚类,将数据集根据数据对象之间的相似度分成多个类别,然后再通过缺失值记录与上面的多个类别进行相似度计算,使用相似度最高的那个类中的数据对象属性均值填充,可以很正确地填充缺失值。尤其是改进后的基于DBSCAN 的缺失值填充算法具有更高的正确率,因为改进后的基于DBSCAN的缺失值填充算法可以对多密度数据集进行聚类,可以得到质量更高的聚类效果,所以填充的正确率也就更高。但是随着缺失比例的增大,上面算法都会有所下降,因为随着缺失比例的增大,缺失值记录包含的信息不够反应这条记录的信息,也就失去了这条数据的价值,因此正确率会明显下降,当缺失比例达到一定程度的时候,缺失值记录就失去了数据的价值,应当予以舍弃。
4 结语
本文提出了基于DBSCAN 的数据缺失值填充算法,针对传统DBSCAN算法不能运用在多密度数据集环境下,传统的DBSCAN算法通过固定邻域半径ε 识别聚类,这就会导致选取过大的邻域半径ε就会将密度大的两个类合并到一个类中,还会把噪点也聚类到类中,而如果选取过小的邻域半径ε 就会把密度较小的类标记为噪点,针对以上缺点,本文通过借鉴图的强连通分量,定义了MinPts 邻域,可以自适应地根据数据对象的密集程度自动调整邻域大小,能够很好地识别出多密度聚类,也就能得到质量更好的聚类效果,这样在缺失值记录填充的时候会得到更加准确的属性值。在改进的基于DBSCAN 的数据缺失值清洗算法中,在计算缺失值记录和完整集中的多个聚类相似度时,运用三角不等式定理,极大地减少了不必要的计算和比较,提高了算法的运行效率。

