基于ICA 优化SVR 的风电场短期风速预测∗

尤亚锋 周武能

（东华大学信息科学与技术学院 上海 201600）

1 引言

风能作为新能源的一种类型，在当今社会发展中处于举足轻重的位置。能源对于经济的发展是不可替代的。目前国内外已经建立许多大型风电厂用于风力发电，风速的大小直接决定风能出力的多寡。由于风速的随机性以及影响因素不定，风速的精准预测是一个重要的问题。短期风速风功率预测可以给电网调度和控制提供依据，有效减小风功率对电网的影响，增强系统的安全性、可靠性和可控性［1］。因此提出一种能够比较精确预测风速的模型是优化风能结构的关键一步。

目前关于风速预测的算法也比较丰富，例如文献［2］采用基于时间序列的BP神经网络进行预测，但是不能克服BP神经网络本身易陷于局部最优解的缺陷，本文将其作为对比算法加以验证。文献［3］采用空间相关法与径向基神经网络相结合来进行预测，取得了不错的效果；文献［4］利用高斯回归的方法进行短期风速预测；文献［5］使用了优化的最小二乘支持向量机算法进行短期预测；文献［6］采用自适应粒子群优化支持向量机回归的算法，获得了较高的预测精度和鲁棒性。支持向量机（Support Vector Machine，SVM）作为新的机器学习算法，对小样本、非线性、高维数的样本数据有较好的适应性［7］。支持向量机（SVM）不但能够较好解决分类问题，而且能够用于回归问题预测。支持向量机回归（Support Vector Regression，SVR）就是用支持向量机作回归分析或者预测。在其他的领域，如模式识别、分类预测等也大量用到支持向量机技术。

2 支持向量机回归理论

SVR以统计学习理论为基础，基于结构风险最小化原则，样本泛化性能极强，避免了对样本数据的高度依赖［8］。 与人工神经网络算法相比，SVM避免了神经网络中拓扑结构难以确定和局部量最优问题，并克服了“维数灾难”［9］。所以，支持向量机广泛应用于各种实际问题当中。

其中模型的构建对于结果准确度具有重大影响，这就涉及到了支持向量机的主要影响参数，包括惩罚因子C、核函数参数Υ、时间延时迟τ、嵌入维数E。

对于支持向量回归机，惩罚因子和核函数参数的选取影响支持向量回归机模型的个数和训练模型的泛化能力［10］。惩罚因子C 的作用是在对样本分类错误的情况下进行惩罚，其值越大表明越重视损失。随着C 的增大，总能实现更加正确的分类，此时会产生过拟合现象，使得泛化能力相对较差。对于核函数，不同的核函数对应不同的回归算法，目前研究较多的核函数如下［11］：

1）多项式核函数

式中：c≥0，d为任意的正整数。

2）高斯径向基核函数

式中：γ＞0 为核参数，表示核函数宽度。

3）Sigmoid核函数

式中：υ＞0，c＜0。

4）傅里叶核函数

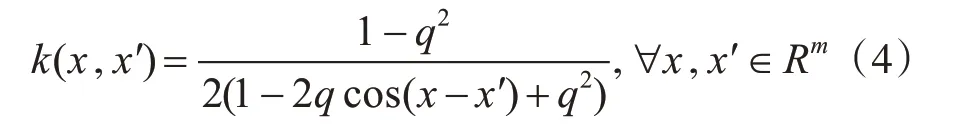
式中：q为满足-1＜q＜1的常数。

本文中选取RBF作为核函数，其参数数目相对较少，且数值限制条件少，可降低模型的复杂性，提高训练速度［12］。

SVR 应用于回归拟合分析，其基本思想是寻找一个最优分类面使所有训练样本离该最优分类面的误差最小［13］。其在高维特征空间中建立的线性回归模型为

式中：ω表示函数权向量，b 为函数阈值，φ(x)为非线性映射函数。一般情况下支持向量机的回归问题可以表示为以下规划问题：

约束条件如下：

为解决线性可分带来的凸二次优化问题，这里利用对偶技巧将其转化为如下问题：

因此风速的回归函数模型可以写成：

3 帝国竞争算法基本原理

帝国竞争算法是不同于粒子群算法、遗传算法、萤火虫算法等仿生算法的一种社会启发式智能寻优算法。在算法中，每一个个体都被定义为一个国家，同时，所有的国家被分类为两类，即帝国主义国家和殖民地［14］。目前，帝国竞争算法以及广泛的应用于解决各种实际问题当中，如参数寻优［15］，调度问题［16］等。与其他优化算法相比，帝国殖民竞争算法在运算时间和优化效果方面显示了其优越性［17］。基于此理论，本文采用帝国竞争算法优化支持向量机的相关参数来获得更加准确的风速预测模型。

帝国竞争算法主要包括四个部分：帝国集团的初始化、帝国集团的同化、帝国集团的竞争与总体适应度计算、帝国灭亡。帝国殖民竞争算法中国家的成本是评价国家优劣的标准，国家的成本越小越好［18］。

3.1 帝国集团的初始化

在帝国集团的初始化阶段随机生成若干权力不等的国家，这些国家按照权力大小又可以分为帝国主义国家和殖民地国家。将殖民地国家分配给帝国主义国家，帝国主义国家及其附属的殖民地国家共同组成帝国集团。对于一个优化问题涉及到的所有解向量可以包含在如下解向量里：

其中：xn表示待优化向量。

第m 个帝国主义国家分得殖民地国家个数计算如下［19］：

式中：其中，Cm表示第m 个国家的代价值，Pm表示第m 个国家的适应度，Nc表示帝国主义国家初始殖民地个数，Ncol表示殖民地国家个数，Nimp表示帝国集团个数。

3.2 帝国集团的同化

随着帝国集团的产生，同化是发生在帝国集团内部的演变。为了完成对殖民地的有效统治，帝国主义国家必须将自己在经济、文化、生活等方面的影响逐步渗透到殖民地国家中去，从而实现对殖民地国家的绝对掌控。这种同化通过殖民地国家的移动来实现。但是在殖民地国家移动的过程中，如果其包含的势力超过所属帝国主义国家的势力，那么殖民地国家与帝国主义国家角色互换，即殖民地国家变为帝国主义国家。

3.3 帝国集团的竞争与总体适应度计算

帝国集团除了内部之间的同化机制外，还会与其他帝国集团发生相互竞争的行为，称之为帝国集团的竞争。势力强大的帝国集团通过吞并弱小帝国集团殖民地国家的方法来扩大自己的统治范围，此处势力代表帝国集团的总体适应度值。这种被吞的殖民地国家指的是最弱的帝国集团中最弱的殖民地国家。整个帝国集团的适应度公式计算如下：

式中：Tc为第m 个帝国集团总体适应度，ξ∈(0,1)表示殖民地国家在该帝国集团总体适应度所占的贡献，fimp,m表示第m 个帝国集团中帝国主义国家的适应度值，Nc表示帝国主义国家初始殖民地个数，fcol,i表示帝国集团中第i 个殖民地国家的适应度值。

3.4 帝国灭亡

伴随着帝国集团之间竞争的不断进行，较弱的国家终将被强国所吞并，当帝国集团中所有的殖民地丢失完后，该帝国走向灭亡。最终只留下最强的一个帝国集团，此刻算法结束并取得特征向量解，否则算法继续迭代，直至找出最优参数组合即是支持向量机最佳参数组合。帝国竞争过程如图1所示。

图1 帝国竞争过程

4 实验分析

4.1 原始数据预处理

本文实验数据来自某风电场连续实际测得的7 天共336 个风速数据，平均每30min 取一次观测点。其中前5天240个数据用作训练集来产生训练样本，后2天96个数据用于测试。为加快算法收敛速度，提高预测精度，本文采用的是比较普遍的基于历史风速数据的预测方法，即依据前2 个小时的4 个风速数据作为样本的输入特征向量，输出则采用下一点的风速数据。本次训练样本作了归一化处理将数据映射到［0，1］变成无量纲形式，从而提高了求解速度，最终结果需要作反归一化处理。本次输入输出特征向量的样本集表示如下：

其中，Xi,Yi表示第i 个样本集的输入输出特征向量。

对于测试集数据，将已经取得预测的数据作为输入向量的一部分，用来预测输出，依次迭代至获取所有预测风速数据。

4.2 风速预测模型的建立

本文算法的主要步骤如下：

1）对帝国集团初始化处理，选出势力较大的帝国主义国家和殖民地国家；

2）帝国集团的同化，帝国主义国家对殖民地国家进行思想和行为上的同化；

3）国集团之间进行竞争，适应度较大的帝国吞并适应度较小的帝国；

4）最终帝国灭亡，在帝国吞并的过程中弱小国家的殖民地完全丢失后，帝国灭亡算法停止，取得最优参数；

5）将取得的最优参数代入支持向量机模型训练样本并预测风速。

本次通过帝国竞争算法获取的惩罚因子C、核函数参数γ 的最优组合为(C,γ)=(71.2,0.0138) 。本次算法流程图如图2所示。

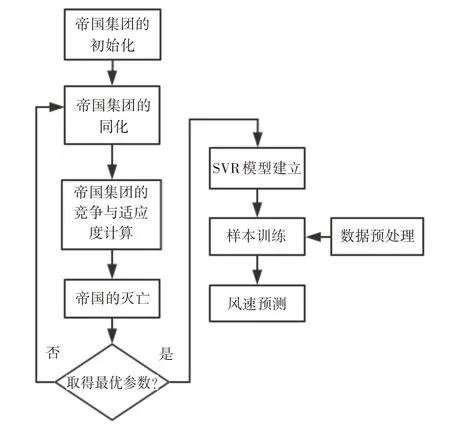
图2 帝国竞争算法优化支持向量机回归的风速预测模型

4.3 风速预测模型评估

为了能够更加直观地描述预测的精度，衡量本次优化后模型的性能，本文采用了四种常用的误差判别方式。

1）均方根误差RMSE（Root Mean Square Error）

2）平均绝对误差MAE（Mean Absolute Error）

3）平均绝对百分比误差MAPE（Mean Absolute Percentage Error）

4）相关系数R

式中，fi表示实际风速，f 表示实际风速平均值，yi表示预测风速，y 表示预测风速平均值。N 为样本容量，RMSE、MAE、MAPE的值越小、R越接近1，模型精度越高。

4.4 风速结果预测

本文将BP 神经网络，未经优化的SVR 算法作为ICA优化SVR的对比算法，其预测结果曲线与误差如图3和表1所示。

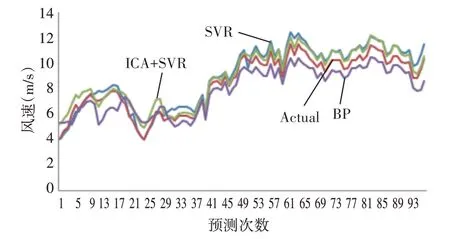
图3 三种模型预测结果对照图

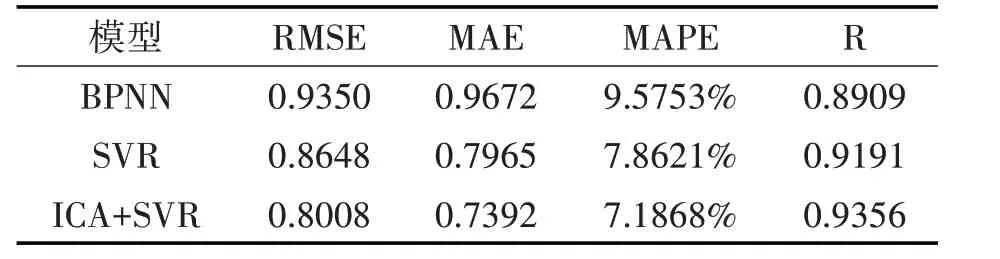
表1 三种不同模型下预测误差分析

5 结语

通过本文的研究分析可以得出，建立的三种风速预测模型均能够模拟风速变化的趋势，经帝国竞争算法优化后的支持向量机回归模型在误差表现上优于BP神经网络和未经优化的支持向量机回归模型。图3 可以看出误差较大的预测点多出现于风速波动较大的拐点处，且三种预测模型在前期的表现优于后期。由此可以看出由于风速预测的不确定性和随机性，对于相对较长时间的风速预测，还应该更加深入挖掘风速变化的潜在规律，随着未来深度学习技术、智能优化算法的崛起，模型的精确度还有待进一步提高。