基于A*初始解的禁忌搜索算法优化及仿真应用∗

刘婷婷 高 尚

（江苏科技大学计算机学院 镇江 212003）

1 引言

无人驾驶汽车在某种性能参数的作用下，索引一条自起点至目标终点的最优级、次优级无碰路径，这种技术被人们称作路径规划［1］。工作实践中，单点搜索算法极易陷身局部最优的状况，禁忌搜索算法的出现，为求解车辆路径问题提供了新的工具［1］。禁忌搜索算法简单易于理解，程序容易实现，运行所需时间较短，禁忌表的约束使算法不易陷入局部极小，在无人驾驶汽车的路径规划技术中，这种算法已然引发了相关科研工作者地高度关注。本文针对现有研究中原禁忌搜索算法大多采用有向边排列的解作为表示方法来构造算法，这样的解的表示不够直观，算法策略表现复杂使人难以理解，搜索效率低和收敛速度慢等缺点。提出了引入A*算法确定初始解的改进措施，通过简化解的表示方法来提高其求解路径规划问题的全局寻优能力。在栅格地图法中，通过对其他智能算法的仿真实验表明，改进的禁忌搜索算法全局寻优能力提高，且具有更快的收敛速度和更高的寻优精度。

2 禁忌搜索算法

2.1 禁忌搜索算法基本原理

禁忌搜索算法（Tabu Search，TS）技术是一种在局部邻域搜索的基础上进行扩展的亚启发式搜索技术，是一种逐步寻优算法［2］。局部邻域搜索是在贪婪思想的基础上，对当前解的邻域进行搜索，这样的搜索方式使得邻域的结构和初始解的选取决定了其性能的优劣［3］，这样的搜索结果容易陷入局部极小而无法保证全局最优。而禁忌搜索算法李用一个禁忌表将已经到达过的局部最优点记录下来，并在下一次搜索过程中有选择的避免重复搜索这些点［4］，以此跳出局部最优点［5］。这好比人类的短期记忆，人们不会重复或者有选择的重复刚刚走过的路；同时“遗忘”又使这些禁止在一段时间后失效，最终达到全局优化的目的［3］。

该算法可以简单地表示为

STEP1 选定一个初始解Xnow；令禁忌表H=ф；

STEP2 若满足终止准则，则中止计算；否则在Xnow的邻域N（Xnow）中选出满足禁忌要求的候选集Can-N（Xnow）；

STEP3 在Can-N（Xnow）中选定一个评价值最好的解Xbest，令Xnow=Xbest，更新禁忌表H，重复STEP2；

STEP4 输出计算结果，停止。

2.2 禁忌搜索算法的改进

禁忌搜索算法作为一种启发式随机搜索算法，确定初始解对算法的优化至关重要。1968 年发明的A*算法就是把启发式方法如BFS，和常规方法如Dijsktra 算法结合在一起的算法。A*算法计算敏捷，虽然无法保证寻求最佳路径，A*却一定能够找到一条最短路径［6］。以这样的解作为初始解可以保证优化算法的高效运行。

假设：将局部范围内路面视为一个第一象限坐标图，已知单位长度为1，以任意点为原点，车辆可向任意方向移动，求网格中任意两个给定坐标之间的最短路径。若将已知的坐标距离改为路径上的障碍物或其他代价参数，例如，路段拥挤、路面限行或者交通事故等因素及其组合，就相当于求任意两点之间绕过障碍物且有最短路程或最少等待的通路。

输入：图G=｛（x，y）|x＞0，y＞0｝有一个元定点s和会定点t，障碍物点B，以及每个相邻单位之间路径代价C。

输出：G中从S到T的最短路径的长度。

初始化阶段：

STEP 0：运行A*算法得到一条最短路径，设为初始解。元定点s标记为永久标记Y，对初始解路径上点做临时标记L，令禁忌表为空。

搜索阶段：

STEP 1：将与永久标记Y 相邻的5 个带有临时标记L 的坐标n，按f（n）=g（n）+h（n）做新的临时标记L。g（n）表示从带有标记Y 的点到任意点n 的代价，h（n）表示从点n 到路径上与标记Y间隔为5的会定点t的评估代价。

在栅格地图中：

计算其最短距离，并将最小点标记为永久坐标Y。

STEP 2：更新禁忌表及当前最优解的记录。

STEP 3：判断f值是否为最小，且路径不经过障碍物，如果是，则f 值在沿着该路径进行时数值恒定。如果否，则将要进行的路径上的f 值均大于恒定f 值。若已经具备最佳f值的结点，算法忽略f 值较高的节点的路径，则删除。重读第2步和第3步，直到取得最优解。

3 数值仿真与分析

3.1 环境建模

为了验证改进后的算法是否在路径规划问题中得到有效应用，本文采用对环境描述较为直接，且容易表示与修改的栅格地图法。设计一个25×25 规模的二维栅格环境模型，每个栅格单元的大小为4m×4m，如图1 所示，黑色区域代表的是未经膨胀处理的障碍物，其余灰色区域表示没有障碍。并将质点以圈状表示汽车的一定体积，保障规划路径与障碍物之间的安全距离。应用改进后的禁忌搜索算法完成从a 点到b 点的安全路径规划，同时还与初始解A*算法（如图1）、人工鱼群算法、蚁群算法以及粒子群算法的仿真结果进行对比分析。

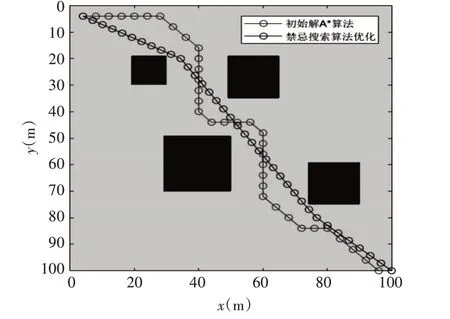
图1 TS-P算法与初始解A*算法对比图

3.2 初始参数设置

应用经验试错法，设置改进禁忌搜索算法（TS-P）；蚁群优化算法（ACO）的功能则是参考文献编程实现［7］；粒子群优化算法（PSO）的功能参考文献实现［8］；鱼群寻优算法（AFSA）的功能则是参考文献的内容编程实现［9］。

3.3 有效性分析

仿真实验的软件平台是Matlab 2017，硬件平台是Windows10的64位操作系统，2.53GHz的主频，4G 的运行内存与Core i5 的处理芯片。各算法所规划的路径效果如图2 中各曲线所示，并将各算法分别运行32 次，统计各算法的平均路径长度（去掉最长路径与最短路径）和平均耗时，结果如表1所示。

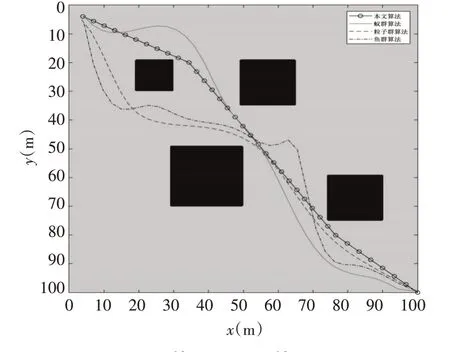
图2 TS-P算法与其它算法对比图

仿真结果显示：A*算法运算时间为0.076，求的距离为164m，采用优化后的禁忌搜索算法，将A*得到的结果作为禁忌搜索的初始值，经过10 次迭代，路径距离为138.49m。其迭代过程如图3 所示，改进后的ST-P 算法经过6 次迭代即可找到最短路径，收敛速度非常快，寻优性能极高。

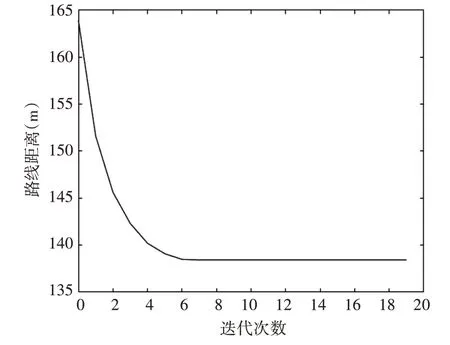
图3 TS-P算法迭代过程图

由图1、图2以及表1可知，初始解A*算法和粒子群算法及鱼群算法虽然较高的时效性，但其规划出的路径过于曲折并且路程较长；而改进后的禁忌搜索算法（TS-P）和鱼群算法（AFSA）的路径比较光滑且长度短，两种算法在时效性方面相差不大，但优化后的TS 算法的路径长度方差明显小于AFSA算法，说明优化后的算法稳定性好。

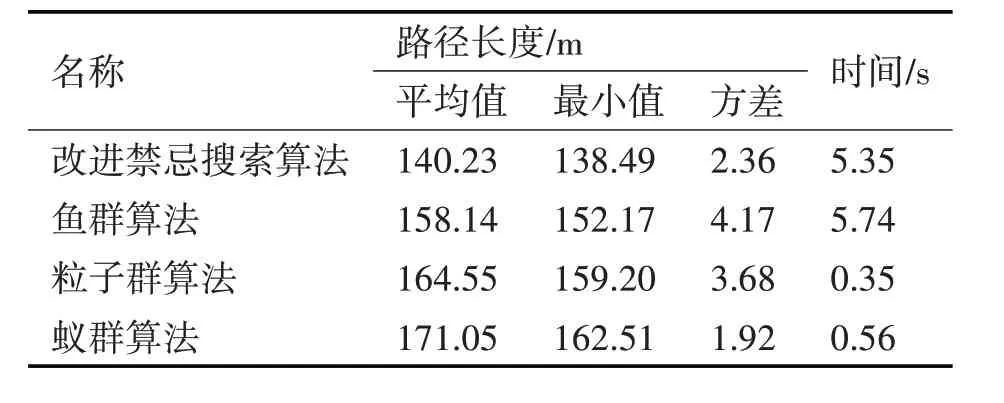
表1 各个算法计算结果统计表

4 结语

禁忌搜索算法是局部搜索算法的扩展，其特点是采用了禁忌表来避免重复前面的工作。相较于其他群智能算法，禁忌搜索算法用一个禁忌表记录下已经到取得的最优解，并且利用禁忌表中的信息必变重复搜索之前的点，简化计算。TS 算法原理简单，计算速度快，易于实现。本文针对原有算法在解决路径规划问题时采用的解的表示方法不够直观，算法策略表现复杂使人难以理解、计算难度大、收敛速度较慢等缺点，提出引入A*算法确定初始解的改进措施，通过简化解的表示方法来提高其求解路径规划问题的全局寻优能力。仿真实验表明，与参考文献中其他智能算法相比，改进后的TS算法在路径规划实例中计算速度和精度都有很大的提高，可用于解决汽车局部路径规划问题的实用高效的智能方法，本文算法有效、可行。