宽带多普勒测速技术中的发射信号∗

黎美琪 王长红 邓 锴

(1 中国科学院声学研究所 北京 100190)

(2 中国科学院大学 北京 100049)

(3 北京市海洋声学装备工程技术研究中心 北京 100190)

0 引言

多普勒测速技术被广泛应用于海洋、医学、气象、军事等领域[1−5]。复协方差频移估计测速法[6−9]简单高效且实时性好，是测频的主要方法。测速数据质量可用偏差及标准差来量化[10]，多普勒频移测量(以下简称测频)误差是载体速度测量(以下简称测速)误差的主要来源，可将测速误差分析简化为测频误差分析[1]。

声波信号作为系统测速的载体，直接影响测速性能，是多普勒测速技术的关键。学者多研究相位编码信号的相关特性[8−9]，缺乏对频谱特性的深入研究。在相关特性方面，文献[8]从自噪声角度论述伪随机二相编码不是最佳波形，以最小方差为目标设计了多相编码信号；文献[9]利用回波自相关第一个旁瓣的位置解决测速模糊。文献[8–9]对信号特性的分析均仅限于相关性，而没有从频谱角度进行分析，本文从频谱角度论述伪随机二相编码不是最佳波形，以最小不对称系数为目标设计差分重复伪随机Blackman 码元幅度调制编码信号。在频谱特性方面，已有关于编码信号频谱特性[11−13]的研究中，一般直接假设时域发射信号为复数形式。如文献[11]推导了复数形式的伪随机二相编码信号频谱表达式，文献[12]介绍了该复数形式编码信号的相关和频谱特性并根据相关性讨论编码参数的选择原则，文献[13]在文献[11–12]的基础上研究了复数形式的非差分重复伪随机二相编码信号的频谱特性，与矩形正弦填充脉冲的频谱进行比较，从频域分析了测速模糊。以上学者均认为编码信号频谱关于载频对称。但实际上，时域发射信号为实信号，不能简单假设为复数形式，编码信号频谱也并不关于载频对称，该不对称主要由正负单边谱旁瓣的相互影响引起。文献[14]指出实数形式的二相调制信号频谱要关于载频对称，需基带脉冲频谱左右频移后的谱没有混叠，即只有高载频才能忽略近似性。文献[1]以常用的伪随机二相编码信号为例对上述不对称性原因进行了简要说明，推导了非差分重复伪随机二相编码信号的不对称系数以量化频谱不对称程度，并指出频谱不对称是测频偏差的重要来源之一。但是文中没有对编码信号的频谱表达式、频谱构成做详细的理论推导及分析，没有对发射信号的形式进行讨论。在雷达系统中，由于大信号的旁瓣会淹没小信号，学者对旁瓣抑制技术进行了较为细致的研究[15−16]，但少有学者将旁瓣与测频误差联系起来。为提高低信噪比条件下的测速精度，往往对编码信号进行重复进而增加发射信号长度[17]，而在编码信号的重复方式上，目前多为简单重复，对差分重复方式的研究较少。且文献[13]中推导得出的重复伪随机二相编码信号频谱表达式仅适用于非差分重复方式，文中给出了适用于非差分与差分两种重复方式的频谱表达式。

本文在文献[1]的基础上进一步分析不同发射编码信号的频谱特性，并基于点回波宽带测频模型分析测频性能。频谱特性方面，推导了不同编码信号的频谱表达式并对频谱的构成及不对称特性进行了详细分析；测频性能方面，基于点回波模型下的复协方差法多普勒频移估计，仿真分析了不同编码信号的测频偏差及标准差。本文对多普勒测速结果校正、发射信号波形设计均具有重要指导意义。

1 伪随机二相编码信号频谱不对称原因分析

宽带测速方式发射编码相干脉冲串信号，比较常用的是伪随机二相编码信号，下面以其为例分析发射信号频谱不对称原因。

一般假设伪随机二相编码信号的复数形式：

其中，ϕ(t)为相位调制函数，取0或π；f0为频率调制载频；a(t)为编码信号幅度调制函数：

其中，L为编码信号码元数，T为码元宽度，LT为单段编码信号时长，根据δ函数性质，复包络可写成

其中，ci为码元编码序列，v(t)为码元幅度调制函数：

实际上发射信号为实信号，伪随机二相编码信号的实数形式为

由于

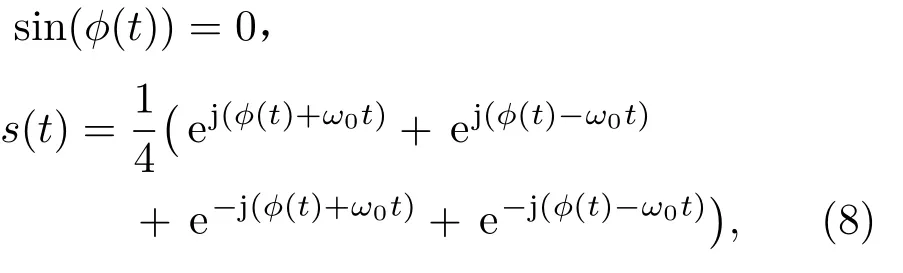
又

则s(t)的频谱S(f)为双边谱：

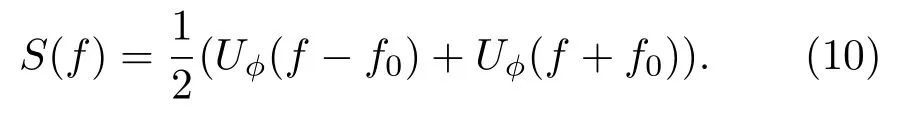
从式(3)、式(5)可以看出，二相调制本质上相当于双极性码元幅度调制，Uϕ(f)完全由码元幅度调制函数v(t)及伪随机码序列ci决定，当单个码元由Rectangle窗调制，V(f)=Tsinc(fT)e−jπfT，对应的(f)旁瓣高、衰减慢；ci决定编码信号相关特性，该特性已在大量文献中被讨论，不再细述。编码信号时域波形可看作子矩形脉冲的叠加，频谱亦可看作子脉冲频谱的叠加。从式(10)可以看出，实数形式的伪随机二相编码信号，在频谱上表现为正负单边谱的叠加，在以往学者的研究中往往忽略了负单边谱。

以采样频率fs= 20 MHz、中心频率f0=600 kHz、编码信号码元数L= 7、填充系数Q= 6、编码序列c= [−1,1,−1,−1,1,1,1]为仿真参数，实数形式的伪随机二相编码信号的时域波形及频谱组成示意图如图1所示。

图1 二相编码信号频谱组成原理Fig.1 Principle of spectrum composition of two-phase coded signals

由码元编码序列c，将信号看作4个子矩形脉冲的叠加，其时域波形如图1(a)所示，at为编码信号，ati(i= 1,2,···,4)为根据相位跳变位置分割所得的4 个子矩形脉冲。由图1(a)可知：不同码符号边界，时域波形幅值反转；每一个码元内填充Q=6个余弦波。信号的频谱叠加示意图如图1(b) 所示，af为编码信号频谱，afi(i=1,2,···,4)为子矩形脉冲对应的子频谱，sum为子频谱afi的叠加。由图1(b)可知：af与sum 完全重合，子频谱叠加得到编码信号频谱，信号频谱旁瓣较高，衰减较慢。子脉冲长度越长，子频谱能量越集中在中心频率附近，但频谱带宽不变，带宽由载频和填充系数决定B=f0/Q。实数形式的伪随机二相编码信号频谱幅值不对称示意图如图1(c)所示，、、S分别为负单边谱、正单边谱、正负单边谱叠加后实信号的真实频谱，由于的符号以−f0为中心，每经过频率长度B即变换正负，且在以f0为中心的±B范围内同符号，故在正频率轴的旁瓣对的影响在f0两侧是相反的(对的影响同理)，造成±f0两侧的频谱不对称。即正负单边谱旁瓣的相互影响导致最终实信号的频谱S在正频率部分不再关于直线f=f0对称。

频谱的以上旁瓣高、衰减慢、不对称特性是由于单个码元由Rectangle 调制。为了减小不对称性，单个码元用Blackman 窗调制，码元幅度调制函数为

编码序列不变，则实数形式的Blackman 码元幅度调制宽带编码信号的频谱为

其中，UϕB(f) =VB(f)C(f)，VB(f)为vB(t)的频域表达。

仿真参数同图1，码元幅度调制函数分别如式(4)、式(11)所示，编码信号的时域波形及频谱结构如图2 所示。图2(a)为分别用Rectangle、Blackman 窗调制码元幅度的伪随机二相编码信号时域波形。图2(b)中、S、SB分别为复数形式的Rectangle 窗码元调制编码信号频谱、实数形式的Rectangle 窗码元调制编码信号频谱、实数形式的Blackman 窗码元调制编码信号频谱。正如前文所分析的，SB较S旁瓣衰减快，不对称程度减小；主瓣展宽且幅度降低。

图2 矩形窗及布莱克曼窗码元幅度调制编码信号时域波形及频谱结构Fig.2 Time domain waveform and spectrum structure of Rectangle and Blackman symbol amplitude modulation coded signals

2 参数对重复编码信号不对称系数的影响

本节给出重复编码信号频谱及不对称系数的数学表示，并重点研究编码信号码元数L、重复次数R、填充系数Q、信号重复方式(差分/非差分)对不对称系数的影响。

参考式(3)，复数形式的重复伪随机二相编码信号复包络可写为

其中，cRi为重复方式序列，非差分重复方式时cR为全1 序列，差分重复方式时，相当于进行了双极性编码信号幅度调制，调制序列为cR= [1,−1,1,−1,···]，由傅里叶变换可得复包络频谱：

根据第1 节中的正负单边谱叠加理论，可得实数形式的重复伪随机二相编码信号的频谱为

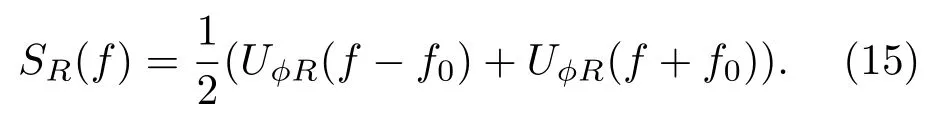
文献[13]中分析非差分重复方式的编码信号频谱时，将式(14)亦写作

由于第1 节中已经对Uϕ(f)进行了详细说明，下面重点分析式(14)中的第二项：

显然e−j2πfkLT为周期函数，假设其周期为∆f，则有

每一个码元由Q个载频为f0的余弦波填充，故单个码元时间长度T=Q/f0，代入式(18)得

即无论重复方式如何，FcR均由一系列间隔为∆f的谱线构成。非差分重复方式时，cR为全1 序列，FcR(f −f0)在f=f0+∆f/2处取值为0，在f=f0时取得极大值，即f=f0处对应一条谱线。差分重复方式时，FcR又可写作

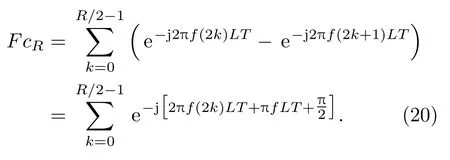
FcR(f −f0)在f=f0处取值为0，在f=f0+∆f/2处取得极大绝对值，即f=f0+∆f/2 处对应一条谱线。

重复次数R=6、编码信号幅度调制序列cR= [1,1,1,1,1,1]或[1,−1,1,−1,1,−1]、其他仿真参数同图1，复数形式的重复伪随机二相编码信号频谱如图3所示。

图3(a)中FcRno、FcR分别表示非差分、差分重复方式对二相编码信号频谱调制的脉冲序列。如前文所分析的，两者均由一系列间隔为∆f= 14.3 kHz 的谱线构成，前者在f=f0处为极大值点，后者在f=f0+∆f/2 处为极大值点。图3(b)中、Rno、R1no、R1分别表示非重复信号频谱(可表示谱包络)、文献[13]推导的非差分重复信号频谱、本文中推导的非差分重复信号频谱及差分重复信号频谱。显然Rno、1no完全重合，即本文推导的结果与文献[13]吻合。图3(b)中较图1(b)中表现了更多频谱细节，因为其为公式直接推导得到，而图1 为时域信号傅里叶变换仿真得到，受频率分辨率影响，图1(b)不能表现全部细节故整体比较平滑。对比分析、R1no、R1，重复编码信号时域上进行周期重复，对应于频域上乘一系列间隔为∆f的脉冲(FcRno、FcR)，从而将频谱离散化，或者称为“频域采样”，频谱包络较近似不变；差分重复编码信号相当于对编码信号幅度再进行cR= [1,−1,1,−1,···]的调制，亦等价为单段编码信号进行一次正负加权叠加后所得的信号进行R/2 次周期重复，该方式改变脉冲位置而不改变脉冲形状，故频谱包络依然近似不变。但是两种方式所得包络对原始信号频谱的表征均不完整，如R1no虽然能够表现f0处的凹陷，但其他位置的凹陷均不能表现；R1则完全相反，能表现除f0外其他全部位置的凹陷。

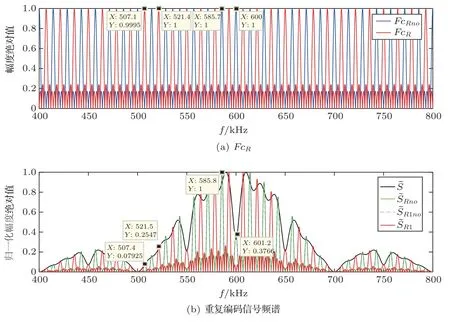
图3 非差分与差分重复编码信号频谱Fig.3 Non-differential and differential repetitive coded signal spectrum

根据以上分析，重复伪随机二相编码信号频谱在正频率轴有如下特点：形状为梳状谱，谱包络近似等于伪随机二相编码信号频谱；谱线以载频f0为中心，在f0、f0+∆f/2处，非差分、差分重复方式为极大值；有相同的频率间隔∆f，且单段编码信号时间长度LT= 1/∆f；在带宽B内非差分方式有2L+1条谱线、差分方式有2L条谱线；f0两侧的频谱幅值不对称，a= (a−L,a−L+1,···,aL−1,aL)表示谱线的幅值向量，非差分方式a0存在，差分方式a0不存在。设立频谱幅值不对称系数εasy以量化频谱不对称程度[1]：

其中，分子表示关于f0对称的两条谱线的幅值，分别与其他所有谱线幅值相乘做差值后的加权和；i表示当前谱线位置；k表示与当前谱线频率相距k∆f；γi= (fi −f0)/∆f为不同位置谱线的加权系数，分母的作用为归一化。

下面仿真εasy随宽带编码信号的参数Q、R、L、重复方式变化的情况。为减小栅栏效应，选取f0= 500 kHz、Q= 4、其他仿真参数未特殊说明时同图3。选取以f0为中心的2B范围内的谱线。不对称系数随各参数的变化情况如图4所示。

图4 中，nodiff、diff 表示非差分和差分重复方式，分别用黑色和红色表示；rec、bla 表示Rectangle窗和Blackman 窗码元幅度调制，分别用方块和星形表示。从整体可以看出红色比黑色曲线更接近直线0，即差分编码方式可减小不对称系数；星形曲线基本接近直线0，远小于方块形曲线的幅度，文中提出的Blackman 码元幅度调制编码信号能够显著降低不对称系数(εasy≈0，可以近似认为频谱完全对称，即该编码信号是以最小不对称系数为目标的最佳波形)。当Q增大，不对称系数整体呈下向降趋势，因为Q越大，带宽越小，单边谱的相互影响就会越小，当Q增大到一定程度，信号接近为窄带信号，不对称系数趋于0；当L增大，不对称系数整体呈上升趋势，因为在一定的带宽内，谱线越密集，谱线间的相互影响越严重，且非严格巴克码的相关性不理想，相应的频谱结构对称性不理想；R基本上不影响不对称系数，因为其不影响整体包络，主要决定单根谱线的分辨率，R越大，编码信号时间越长，频率分辨率越高，谱线越细。

图4 不对称系数随各参数的变化情况Fig.4 The variation of the asymmetry coefficient with parameters

3 几种编码信号测频性能的比较

本节主要分析第2 节中提出的4 种重复编码信号：非差分Rectangle 调制(nodiff+rec)、差分Rectangle 调制(diff+rec)、非差分Blackman 调制(nodiff+bla)、差分Blackman 调制(diff+bla)对测频误差的影响。利用复协方差频移估计测量目标运动速度的流程[10]如图5所示。

图5 复协方差估计频移进而测速的流程图Fig.5 Complex covariance variance estimation Dopplershift and speed measurement flow chart

文献[18]指出，当复相关运算所得相关函数的频谱关于多普勒频移偶对称(不对称系数为0)，多普勒频移估计无偏。假设信号传输环境理想，频谱幅值响应为1(只考虑发射信号频谱不对称性)，由前面两节的分析可知，不对称系数不为0。文献[1]指出相关时延不准确且频谱不对称是测频偏差的重要来源，并建立了基于复协方差法的宽带测频模型，本文利用其点回波宽带测频模型得接收信号

中心谱线f0对应的多普勒频移fd= 100 Hz，接收信号谱线间隔∆ωr= ∆ω(1+ωd/ω0)，n(t)为白噪声，相关时延τ=LT，其他仿真参数同图4。加入与信号频带相同带宽内的噪声，不同信噪比条件下，按图5所示流程进行N=1000次仿真实验，4种信号的不对称系数如表1，测频偏差及标准差如图6所示。测频偏差定义为确定信噪比下，估计多普勒频移均值与真实多普勒频移值fd的差；相对测频偏差定义为测频偏差与真实频移的比值；测量标准差定义为

表1 4 种编码信号的不对称系数Table 1 Asymmetry coefficients of four coded signals

由表1 知，Blackman码元幅度调制宽带编码信号的不对称系数较Rectangle 码元幅度调制低3 个数量级，差分重复方式较非差分方式具有更小的不对称系数。Blackman 窗码元调制信号的不对称性系数已经很小，故差分重复方式对不对称系数的影响不大，差分重复方式在Rectangle 窗码元调制信号中表现出较明显的优势。差分重复Blackman 码元幅度调制宽带编码信号具有最小的不对称系数。

由图6 可以看出，不考虑波束开角的点回波模型下，基于复协方差法的测频性能具有与不对称系数相似的规律。图6(a)表明：Blackman窗码元调制信号对应的测频偏差小于Rectangle 窗码元调制信号；差分重复方式信号对应的测频偏差小于非差分重复方式，高信噪比时，diff+rec 较nodiff+rec的相对测频偏差降低了约2‰,diff+bla 相比nodiff+bla 在偏差上的优势不明显。图6(b)表明：低信噪比时，Blackman 窗码元调制信号对应的测频标准差明显小于Rectangle 窗码元调制信号。总的来看，diff+bla 具有最好的测频性能，其与传统的nodiff+rec相比：信噪比在0∼−10 dB 范围内测频标准差约下降2%∼20%；信噪比高于10 dB 时相对测频偏差约小5‰∼6‰。

综合表1 的不对称系数值及图6 的测频误差分析可知：不对称系数越小，测频偏差、标准差均越小，即测频性能更佳。

图6 不同编码信号及信噪比条件下的测频性能Fig.6 Frequency measurement performance with different coded signals and signal to noise ratio

4 结论

频谱特性方面：二相编码本质上相当于双极性码元幅度调制，当调制窗为Rectangle 窗，编码信号频谱旁瓣高、衰减慢，正负单边谱相互影响导致频谱幅值不关于载频对称；当调制窗为Blackman窗，其频谱结构近似关于载频对称。编码信号频谱不对称程度可由不对称系数量化。对于重复编码信号，其频谱为等间隔离散化的二相编码信号频谱，具有与非重复编码信号相似的谱包络，差分重复方式本质上相当于双极性编码信号幅度调制，差分较非差分重复方式具有更小的不对称系数。

测频性能方面：点回波模型下，基于复协方差法估计多普勒频移，相关时延取值为发射信号长度。当频谱结构对称，测频偏差接近0；当频谱不对称，测频偏差与频谱不对称程度相关。差分重复Blackman 码元幅度调制宽带编码信号较目前常用的非差分重复伪随机二相编码信号具有更好的测频性能，具体表现为：前者比后者的不对称系数低3个数量级；信噪比在0∼−10 dB范围内测频标准差约下降2%∼20%；信噪比高于10 dB 时相对测频偏差约小5‰∼6‰。量化不对称程度的不对称系数越小，测频偏差、标准差均越小，即测频性能更佳。