能量加权时间特征用于浅海声源深度类型判别∗
于梦枭 周士弘
(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)
(2 中国科学院大学 北京 100049)
0 引言
声呐基阵检测到的海上声源目标复杂多样,通常水面声源目标吃水深度在十几米以内,而水下声源目标完全浸水或正常工作深度均在十几米或几十米以下,因此,从多样化的目标类型和复杂变化的特征中脱离出来,解决水面声源和水下声源的深度判别问题,对分类和识别水下声源目标十分重要。
水面及水下声源判别问题一直是水声学领域中研究的难题之一。长期以来,声呐目标识别技术是解决该问题的主要途径[1−2],该途径依赖于对目标数据的获取和训练,由于目标及其工况的多样性、海洋环境复杂性、系统自身条件限制以及用于分类识别的目标特征可分性等多方面因素的制约,声呐目标识别的应用尚存在诸多问题需要解决。从水声物理角度出发,在特定的海洋环境条件下,寻求利用声信号场传播物理特征来判别水面和水下声源值得探索。
用于水面和水下声源判别的声信号场传播物理特征主要包括声源深度或者具有深度差异性的能量、相位或干涉结构特征等,在浅海波导中多从简正模及其干涉结构特征出发进行研究。Shang[3]基于模态滤波技术,使用垂直阵接收声场信号,将包含有限阶简正模的信号分离并转化为带有各阶模态本征函数及声源距离所对应相位信息的向量数据,利用函数正交性及相关算子处理估计声源深度;Yang[4]同样使用垂直阵分解简正模,当实际声场与拷贝场中各阶简正模幅值相关系数达到最大时,其对应深度即为声源深度;Premus 等[5−6]在声线向下折射的浅海波导中使用水平线列阵作为接收阵列,利用多基地声呐回声探测技术及模态滤波器,分析简正模低阶子空间的能量差异,从而实现深度类型判别;郭晓乐等[7]利用消频散变换分离各阶简正模,基于水平波数差与波导不变量的关系实现声源深度估计;李鹏等[8]使用水平阵接收并在已知目标方位的条件下,在模态域进行波束形成,对各阶简正模的模态强度与理论声场进行匹配估计声源深度,其阵元数越多,频带选择越宽,测量精度越高;Conan 等[9]使用水平阵对于简正模进行模态滤波,将低阶简正模与高阶简正模的能量比作为评判量,判别声源深度类型,但方法受阵列孔径影响较大;刘志韬等[10]利用信号自相关函数warping 变换,分离简正模相干项,通过不同深度声源激发的声场能量中,占主导的简正模相干项特征频率不同的性质实现水面和水下声源判别,当频率较高或海深变深或水文环境变得较为复杂后,方法存在一定的困难。以上研究中大多需要对简正模进行分解后再进行深度估计或判别。
水平直线阵作为接收阵列,对频域波束形成后的声场信号做傅里叶逆变换可以获得波束强度-时间分布图。Lee 等[11]基于此提出基阵不变量概念,波束输出最大值对应波束迁移线(Beamformer migration line)的倒数随时间沿固定斜率线性偏移,在信号方位固定且海水声速已知时,该偏移斜率仅与声源距离有关,即基阵不变量,利用基阵不变量方法可以实现声源被动测距。由于各阶简正模存在频散现象,在波束强度-时间分布图中,接收到的各阶简正模分布在不同的时间段内,而声源深度不同时,各阶简正模能量的时间分布也将有所不同。基于以上物理思想,本文将研究一种基于水平线列阵接收以及利用能量加权到达时间特征作为特征量的脉冲声源深度类别判别方法,相比于上述基于简正模或干涉结构特征过滤的方法而言,力求在水平短阵情况下无需进行简正模分解即可进行声源深度类型判别。
1 基本原理
根据简正模理论,浅海波导中远程传播的声压场可表示为

式(1)中,S(f)为声源的频谱,um(·)为第m阶简正模本征函数(关于深度的实函数),km是第m阶简正模水平波数,M为简正模数目,zs为声源深度,zr为接收深度,ρ为海水介质密度,f为频率。
图1 为水平直线阵信号接收示意图,对于N元等间距水平阵接收的信号,经常规波束形成(Conventional beamforming,CBF)后,声压可表示为与扫描角θ有关的函数[11],

式(2)中,θ为信号入射方向与阵列法向夹角,θs为声源真实方位,B(x)=sin(kxNd/2)/sin(kxd/2)为波束指向性函数,s= sinθ,sm= sinϕmsinθs,ϕm为第m阶简正模俯仰角,sinϕm=krm/k,k= 2πf/c。τn= (n −1)dsinθ/c,d为阵元间距,c为接收深度处海水声速,rs为声源距离。

图1 水平线列阵信号接收示意图Fig.1 Schematic diagram of horizontal line array signal reception
对式(2)进行逆傅里叶变换,得到时域表达式:

式(3)中,Re{·}代表实部值,PB+(s,t)为声压的复数表达形式。
波束输出的波束强度-时间分布由式(3)来表示:

波束强度-时间分布图的横轴为扫描波束s,纵轴为时间t。
1.1 方法原理
下面通过仿真示例来具体说明声源深度类型判别方法的基本原理。仿真条件:等声速剖面,海水声速为1500 m/s,海深为70 m;单层半无限海底,海底声速为1700 m/s,密度为1.7 g/cm3,吸收系数为0.2 dB/λ;声源类型为信道冲击响应,信号入射方向为60◦,声源与水平线列阵参考阵元距离为5 km。阵列孔径为441 m,阵元数为64 个,阵元间距为7 m,接收深度为25 m。采用常规波束形成方法获得阵列输出。图2 为声源频率为50∼100 Hz、声源深度为5 m 及40 m 时的波束强度-时间分布图(单位:dB,下同)。

图2 声源频率为50 ∼100 Hz,不同声源深度时的波束强度-时间分布图Fig.2 Beam-time image with different source depth at 50–100 Hz
图2中脉冲宽度皆为0.36 s,脉冲宽度确定方法将在1.3 节中作介绍。声场中,第m阶简正模到达时间为

其中,vgm为第m阶简正模的群速度。而群速度与俯仰角可通过式(6)关联[11]:

当声源频带足够宽且声源方位固定时,各阶简正模的波束迁移线可以连接成一条曲线,即

利用式(7)可解释图2 中各时间点能量最大值对应波束的偏移情况。同时,在脉冲宽度内,各个时间点的阵列输出能量也不同。将脉冲宽度内时间记为ti,波束输出的声强最大值为该时刻简正模贡献的最大能量,记作Ai,Ai=LB(s,i)。由于水面声源激发声场中高阶简正模能量占优,水下声源激发声场中低阶简正模能量占优,两类声源随时间的Ai分布有所不同。以Ai作为权值,对时间ti进行加权平均并构造函数如下:

其中,t1为脉冲到达接收阵的初始时刻。脉冲宽度及脉冲到达接收阵的初始时刻的确定将在1.3 节中作介绍。
该函数利用信号到达时间的加权平均值与脉冲到达接收阵初始时刻的差值来表示不同深度声源的Ai分布,取时间相对量可以减小因声源距离或声速误差带来的影响。通过水平基阵的基阵不变量被动测距方法[11]或其他被动测距方法[12−17]获得声源距离,并在拷贝声场中对函数H在全海深范围内进行统计。一般来讲,水下声源激发的声场中低阶简正模先到达接收器且能量占优,H(zs)较小;水面声源及近海底声源激发的声场中高阶简正模较迟到达接收器且能量占比增大,H(zs)较大。考虑船只吃水深度等因素,在海深不小于几十米的浅海海域,本文定义深度大致在15 m以上的声源为水面声源,15 m 以下的声源为水下声源。
1.2 工作频率选取
对于理想波导,简正模垂直波数[18]为

式(9)中,m= 1,2,···。各阶简正模本征函数可表示成

研究发现,水面和水下声源深度类型判别阈值深度与简正模本征函数在水面下的第一个节点深度有关,并可以此确定声场中最高阶简正模的阶数,从而根据截止频率公式计算最高工作频率。由式(9)可知,kzmz∗=π.因此,判别阈值对应的深度可近似表示为

反过来,若要以z∗≈15 m 作为水面和水下声源判别的基本依据,那么应满足

根据截止频率计算公式,可得到用于判别处理的最高频率

以上是理想波导中最高工作频率的计算过程。针对一般波导,已知声场环境参数后,在拷贝场中计算各阶简正模的本征函数随深度变化示意图,可选择第一节点深度最接近15 m 的简正模阶数作为M,在此也可将海深D带入式(12)中计算得到M,从而计算工作频段的最高频率。此时最高频率计算公式为

以1.1 节的环境参数为例,此时声场中的前6阶简正模本征函数归一化幅度示意图如图3 所示。由图6 可知各阶简正模第一节点深度最接近15 m的是第5 阶简正模,节点深度为15.22 m。将海深D带入式(12)同样求得M= 5。根据式(14)的计算f∗约为102.46 Hz,故本文选取的工作频段为50∼100 Hz。值得注意的是,在选取工作频率时不宜过低,使得声场中仅存1阶简正模,从而导致判别方法性能下降,甚至失效。
考虑到实际应用情况,本文忽略近海底深度范围(这里选取为海底以上深度15 m 范围),选择声源深度为15 m的H值作为判别阈值,即

忽略的深度范围可根据实际海上环境进行适当调整。一般情况下,Q值的确定需要考虑声源距离rs和方位θs以及基阵接收深度zr的影响。最终由实际声场中计算得到的与拷贝场中的阈值进行对比,判断目标为水面声源或水下声源,即

Q值的确定应在一定频带范围要求下进行,以确保能够利用波导中低阶、高阶简正波的时间扩展及其能量分布特征。

图3 前6 阶简正模本征函数归一化幅度示意图Fig.3 Normalized amplitude schematic diagram of first six order normal mode eigenfunctions
图4 为声源距离5 km、 工作频段分别为50∼100 Hz 及70∼120 Hz 时,函数H在全海深范围内随声源深度变化情况。在忽略近海底附近范围后,由图4(a)可知,深度15 m 声源H值为0.09984 s,即选取阈值Q= 0.09984 s 后,可通过H值与阈值的比较判别声源深度;而图4(b)中,最高频率超出理论计算值。此时深度15 m 声源的H为0.0822 s,即阈值Q=0.0822 s,但深度27 m 声源的H为0.088 s,大于阈值Q,会被判定为水面声源,即当最高工作频率高于102.46 Hz 时,会使得方法出现误判的情况。在此情况下,若因客观因素必须使用该频段时,则可以通过选择水下声源H的最大值作为阈值解决该问题,阈值深度根据选定阈值映射至15 m附近,此时判别深度类型时出现一定的误判深度区间,图4(b)中若选择0.088 s 作为阈值,其阈值深度映射至14.4 m 附近,出现0.6 m 的误判深度区间,工作最高频率越高,误判区间越大。故应尽量满足工作最大频率小于理论计算值以保证方法的有效性。

图4 不同声源频率时,H 值随声源深度变化情况Fig.4 Variation of H versus source depths at different frequency
1.3 脉冲宽度及脉冲到达接收阵初始时刻的确定
若脉冲宽度及脉冲到达接收阵的初始时刻误差较大,计算得到的H值将受到较大影响,所以确定以上两物理量十分重要。在脉冲宽度内,根据式(7),声强最大值对应波束的倒数随时间的偏移线斜率固定,可以根据该性质确定脉冲宽度和脉冲到达接收阵的初始时刻。图5 为声源深度5 m 时声强最大值对应的波束倒数随时间变化示意图。

图5 波束迁移线的倒数随时间变化示意图Fig.5 Schematic diagram of the reciprocal of beamformer migration line versus time
图5 中t1为脉冲到达接收阵的初始时刻,te为脉冲结束时刻。在时间为3.33∼3.69 s的区间内,声强最大值对应波束的倒数产生小幅波动,但可近似认为随时间沿一定斜率变化。而当时间小于3.33 s及大于3.69 s 的区间内,不再存在这种规律,由此确定t1= 3.33 s,脉冲宽度为0.36 s,时间区间为3.33∼3.69 s。
2 性能分析
下面考察在不同声源距离、方位、海深以及接收深度和阵列孔径的条件下方法的性能。仿真参数同第1节,声源频率为50∼100 Hz。
2.1 声源距离
图6 为声源距离分别为5 km、10 km 及20 km时,H函数值随声源深度的变化情况。

图6 不同声源距离条件下,H 值随声源深度变化情况Fig.6 Variation of H versus source depths at different source range
由图6 可知,不同的声源距离对应于不同的H曲线,阈值也有所不同。距离变远时,脉冲宽度增加,各阶简正模到达时间差异变大,且相比于低阶简正模,高阶简正模的能量衰减要大,因而阈值变大。可见,式(14)中Q值的选取应根据声源距离的变化而改变,例如,图6 中5 km、10 km 和20 km 时的阈值分别为0.09627 s、0.1712 s、0.2339 s。当给定了声源距离所对应的合适的Q值,即可实现声源深度类型判别。
2.2 声源方位
图7 为声源从不同方位入射时,H函数值随声源深度的变化情况。

图7 不同声源方位条件,H 值随声源深度变化情况Fig.7 Variation of H versus source depths at different source azimuth
由图7可知,对于不同方向入射的信号,H值随声源深度变化情况接近,表明阈值Q及阈值深度与声源方位近似无关。需要指出的是,如果信号从正横及其邻近方向入射,入射角的正弦值为0,此时波束强度-时间分布图中可能无法产生波束迁移线,因此实际应用中无法通过1.3 节方法确定脉冲宽度及脉冲到达接收阵初始时刻,可能导致H值计算出现误差,造成误判的情况。而从端射方向入射时也可能会对高阶简正模不敏感,应尽量避免使信号从阵列正横及端射方向入射。
2.3 海深
验证在不同的海深时,根据1.2 节的频率选定标准,方法是否可行。海深为100 m 和200 m 时,本征函数第一节点深度最接近15 m 的简正模阶数分别为第7 阶和第14 阶,计算最大工作频率分别为103.59 Hz及107.58 Hz,频率选择50∼100 Hz。图8为海深为100 m 及200 m 时,H函数值随声源深度的变化情况。
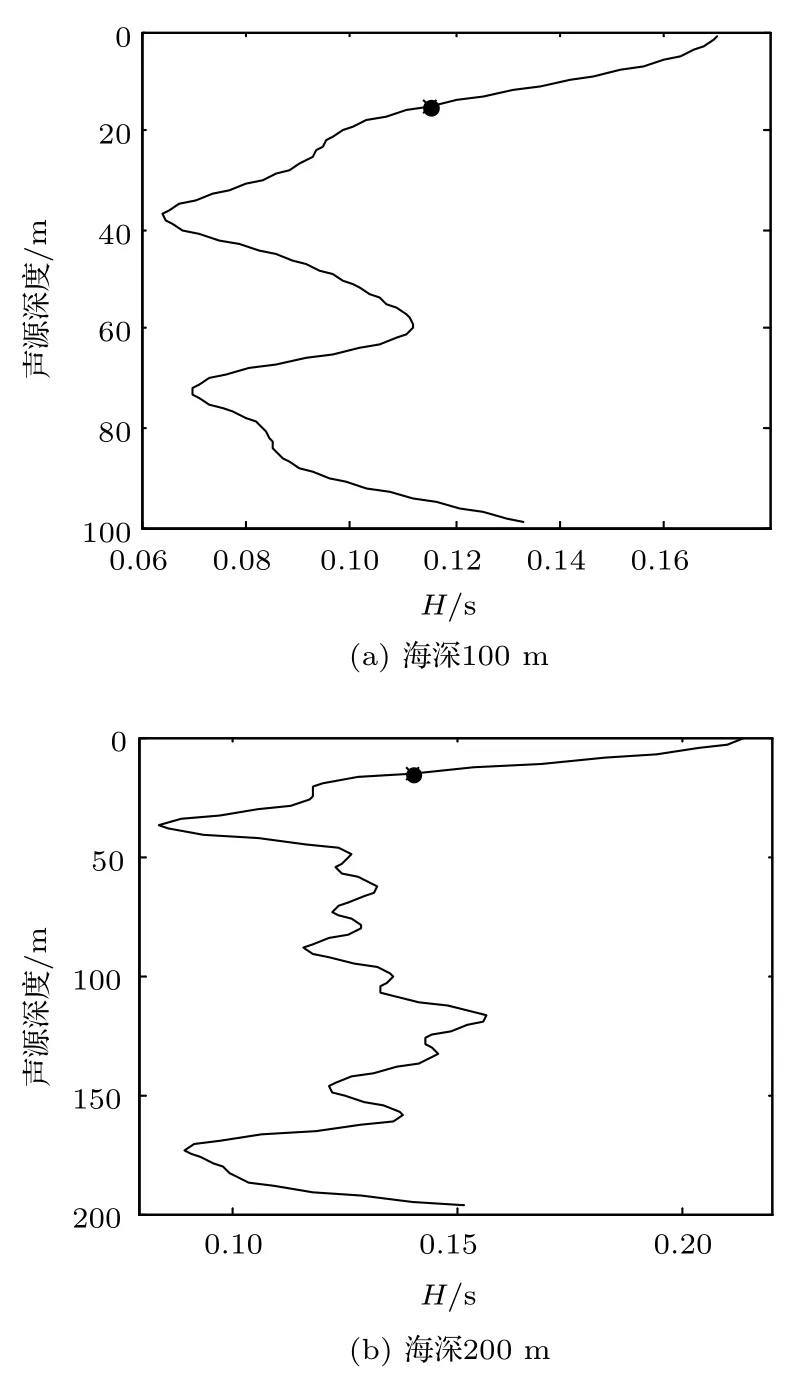
图8 不同海深条件下,H 值随声源深度变化情况Fig.8 Variation of H versus source depths at different sea depth

图9 阵深70 m、海深200 m 时,H 值随声源深度变化情况Fig.9 Variation of H versus source depths at horizontal line array depth of 70 m and sea depth of 200 m
由图8 中标记黑点为声源深度15 m 时的H值,在海深为100 m 及200 m 的条件下,在不改变接收器深度时,通过拷贝声场中H值曲线确定阈值后,可能会导致声源深度类型误判,如图8(b)所示,在深度119 m 附近的声源会被判定为水面声源。而将接收阵深度改为70 m 时,如图9 所示,此时误判区间消失。这是由于不同的接收深度对各阶简正模的敏感性不同,具体内容会在2.4节中分析。海深的改变不会影响方法的性能。
2.4 水平阵接收深度
在布置水平阵时,要考虑不同接收深度对于各阶简正模敏感性的问题。图10 为水平阵分别布置于25 m、30 m 和69 m 深时,H函数值随声源深度的变化情况。根据图3 中前5 阶简正模本征函数随深度变化情况,深度25 m 位于简正模第3 阶节点位置附近,深度30 m非任意阶简正模节点,深度69 m低阶简正模幅度较小,高阶简正模幅度较大。

图10 不同的水平阵深度,H 函数值随声源深度的变化情况Fig.10 Variation of Hversus source depths at different horizontal line array depth
由图9 可知,当水平阵布置于69 m 时,水下声源的H值与阵深25 m及30 m时差异较大。由于海底附近位置的低阶简正模本征函数幅值较小,接收阵对于低阶简正模敏感性变弱,第1 阶简正模尤为明显。水下声源第1阶简正模的能量占比大,因此对其H值改变明显。但在已知接收深度和忽略近海底附近范围的前提下,依旧可以根据Q值,对声源进行深度类型判别。不同的条件使用不同的阈值,对于水面与水下声源深度类型的判断性能影响无影响。方法在阵任意深度皆可使用,但值得一提的是,在布置水平阵的接收深度时,应尽量保证低阶简正模良好的敏感性以获得水面、水下声源区别较大的函数H曲线。同理,接收阵对于声场中激发的最高阶简正模也应保证良好的敏感性,保证脉冲宽度判断的准确性,有利于获得较好的声源深度类型判别性能。这也解释了2.3 节中海深为200 m、接收深度为25 m时,出现了误判深度区间的原因。
2.5 阵列孔径
不改变阵元间距,图11为32 个阵元,即阵列孔径为217 m时,声源深度为5 m及40 m 时的波束强度-时间分布图。图12 为32 阵元与64 阵元条件下H函数值随声源深度的变化情况的对比。

图11 阵元数为32 个时,不同声源深度波束强度- 时间分布图Fig.11 Beam-time image with different source depth when the number of array elements is 32
将图11(孔径217 m)与图2(孔径441 m)进行对比可知,当阵列孔径为217 m 时,波束输出方位谱的主瓣宽度明显增加。两种阵列孔径条件下,水面声源对应的H函数值略有差别,而水下声源对应的H函数值则近似不变;由图12 可知,阵列孔径为217 m 条件下,H函数值随声源深度的变化情况与阵列孔径为441 m的H函数值差异很小。这说明尽管接收阵孔径影响接收阵波束分辨力和空间增益,但对由波束输出声强提取的能量加权时间特征随深度的分布关系而言影响较小。

图12 不同的阵列孔径,H 函数值随声源深度的变化情况Fig.12 Variation of H versus source depths at different array aperture
2.6 水文类型
下面在负梯度水文环境及温跃层水文环境中验证方法的可行性。声速剖面如图13所示,其中温跃层的跃层深度为15∼25 m。图14为两种水文环境下H函数值随声源深度的变化情况。可见,在负梯度及温跃层水文条件下,方法依然保持了对水面声源和水下声源的可判别性。

图13 负梯度及温跃层水文环境的声速剖面Fig.13 Sound speed profile of negative gradient velocity and thermocline
3 失配分析
下面考察声源距离、海底纵波声速、海深参数失配时方法的鲁棒性。仿真参数均第1 节的模型为基础,声源频率选取50∼100 Hz。
3.1 声源距离失配
声源距离是本文方法进一步判别声源深度的前提条件,因为声源距离会影响到拷贝场计算值的准确性,但实际应用中,声源距离的估计值会存在误差,因此有必要讨论方法对于声源距离失配的鲁棒性。图15为声源距离分别设置为4 km、5 km、6 km时H函数值随声源深度的变化情况。
由图15 可知,不同声源距离的H值随深度的变化趋势接近。随着声源距离的增加,低阶简正模与高阶简正模到达接收阵的时间差增加,同时水面声源中到达接收阵列较晚的高阶简正模能量占优,从而使得水面位置H值随着距离增加而变大。
距离失配导致实际声场与拷贝声场各阶简正模到达时间及脉冲宽度有所差异,但差异量很小,相邻两阶简正模的到达时间差在10−2秒级以下,由于H为时间相对量,受小范围变化的距离影响也非常小,因此较小的声源距离失配对于判别阈值影响很小,方法对于声源距离失配具有较好的鲁棒性。
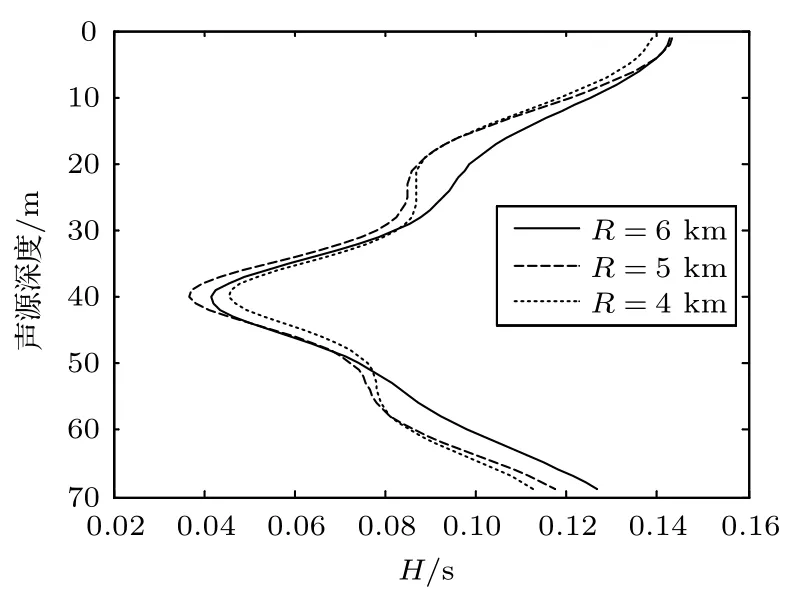
图15 声源距离小范围变化时,H 值随声源深度变化情况Fig.15 Variation of H versus source depths due to the mismatch of source range
3.2 海底纵波声速失配
图16 为海底纵波声速分别为1650、1700、1750 m/s时H函数值随声源深度的变化情况。

图16 不同海底纵波声速时H 值随声源深度变化情况Fig.16 Variation of H versus source depths due to the mismatch of bottom longitudinal wave velocity
海底纵波声速的失配将影响声场中简正模激发阶数及本征函数在深度上的分布。图17为声源深度30 m、不同海底纵波声速条件下的时频分析图,由图17可知,海底纵波声速为1650 m/s时,在25 m的接收深度下(第3 阶简正模本征函数节点位置附近),声场中激发两阶简正模(1 阶、2 阶),第4 阶可以忽略不计,与其他海底纵波声速环境(1阶、2阶、4阶)有所不同。

图17 海底纵波声速为1650 m/s、1700m/s 和1750m/s 时信号时频分析图Fig.17 Signal time-frequency analysis image corresponding to bottom longitudinal wave velocity of 1650 m/s,1700 m/s and 1750 m/s respectively
当简正模总阶数变少时,脉冲宽度变短,H值变小。根据图16中H值随声源深度变化情况及2.3节关于海深变化的性能分析可知,声场中简正模的阶数虽然对方法影响较小,但不同阶数情况下,水面与水下声源的判别阈值却有所差异,所以,当海底纵波声速失配导致声场中出现简正模阶数失配时,方法性能则可能下降。因此在实际应用中应通过底质采样、反演以及资料查询等手段尽量保证海底纵波声速的准确性。
3.3 海深失配
海深的失配同样会影响本征函数随深度的分布情况。3.2 节中已提到,若拷贝声场与实际声场激发的简正模阶数不同,H值差异较大,会导致方法性能下降,本节仅考虑激发简正模阶数相同时,方法对于海深略有失配时的鲁棒性分析。图18 为海深分别为70 m、72 m 及75 m 时,H函数值随声源深度的变化情况,海深70 m。由图18 可知,在不影响声场中简正模阶数的情况下,海深略有失配对方法产生的影响可忽略不计。
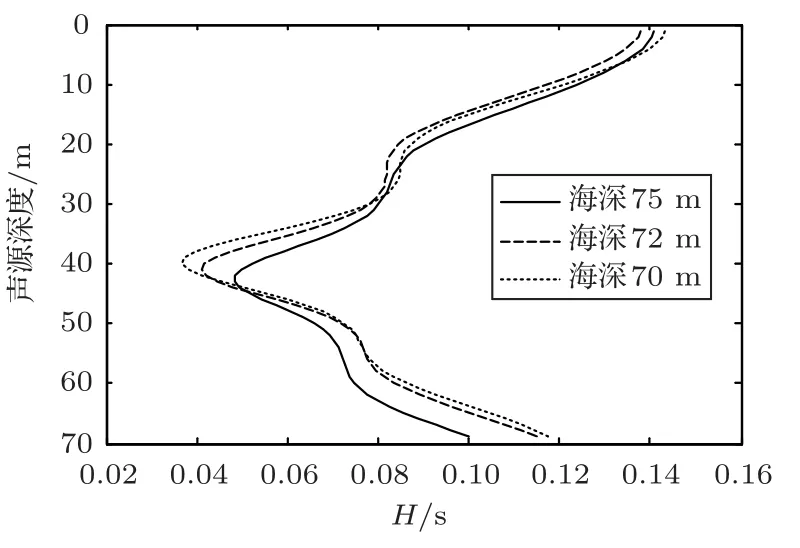
图18 不同海深,H 函数值随声源深度的变化情况Fig.18 Variation of H versus source depths due to the mismatch of water depth
4 结论
根据简正模理论,各阶简正模到达接收器的时间有所不同,简正模阶数越低,群速度越大,到达时间越早。利用水平直线阵作为接收阵列,可获得波束强度-时间分布图,在脉冲宽度内对每一时刻的阵列输出最大声强值(即该时刻信号的能量)进行搜索,以其作为权值,计算各阶简正模到达时间的加权平均值。构造函数H,将信号到达时间加权平均值与脉冲到达接收阵的初始时刻相减,以表示简正模高低阶能量的分布情况。在环境参数及声源距离已知的前提下,可以获得拷贝声场中水面与水下声源判别阈值,将实际声场中值与拷贝声场中判别阈值进行比较,实现宽带脉冲声源的深度类型判别。
在具有一般性意义的等声速浅海波导条件下进行数值仿真表明,以第一节点深度最接近15 m的某阶简正模的截止频率为上限,给出工作频率选取准则。无参数失配时,方法对于定义的水面与水下声源界限方法判别效果好。声源方位及声源距离、海深、阵接收深度和阵列孔径均不影响方法性能。有参数失配时,除海底纵波声速失配对方法影响较大外,方法对于其他参数(如声源距离、海深等)的失配鲁棒性好,同时方法可在负梯度及温跃层水文环境下使用。

