基于动态阈值匹配追踪的主动声呐直达波抑制方法∗

张 蒙 王海斌 汪 俊 张海如

(1 中国科学院声学所 声场声信息国家重点实验室 北京 100190)

(2 中国科学院大学 北京 100049)

0 引言

主动声呐系统中，为了进一步提高探测性能，通常采用长脉冲信号获得时间累积增益。但是，在多基地主动声呐中，回波传播损失较直达波更严重，两者的能量传播损失相差数十分贝。延长探测脉冲宽度会带来更为严重的直达波干扰，从而导致更大的探测盲区，该问题需要通过直达波抑制技术(Direct blast suppress,DBS)解决。直达波抑制问题是双基地声呐探测中的关键技术难题之一[1−2]，已有诸多学者针对该问题进行了研究。

现有的直达波抑制方法一类是从波束旁瓣控制的角度进行的。文献[3]根据波束旁瓣控制技术，提出了一种基于高阶零点约束的直达波抑制方法，该方法扩展了静态权向量中的零点宽度，提高了干扰抑制的稳健性，但是由于声波在浅海信道传播时各号简正波群速度存在较大差异，很难通过零点约束有效抑制直达波干扰。波束旁瓣对消技术[4−7]通过主辅通道自适应对消抑制直达波干扰。该方法选取较近的接收器作为主辅通道，这样直达波信号可以认为经历了相同的信道传播，信道影响相互抵消，因此，旁瓣对消法对信道引起的信号畸变不敏感。但由于声呐中直达波信号与回波信号的相干性，抑制直达波的同时会抵消回波等有用信息，影响声呐检测性能。文献[8]中提出了利用强干扰方位输出信号作为参考信号进行对消的后置干扰抑制方法，在提高干扰抑制效果的同时避免了回波等有用信息的损失，但是该算法需要先对干扰进行测向；另外水声信道中，信号的纵向相关性下降较快[9]，为了保证算法性能，需要对阵元接收信号的相关性进行补偿。

另有一类方法是通过设计信号波形进行直达波抑制。代表性的方法是文献[10]提出的声屏蔽技术抑制直达波，可以在消除直达波的同时，有效保留回波信息，具体方法是根据测量的信道设计波形，使信号在接收点处形成零点，达到抑制直达波的目的。这种方法适合固定的声呐系统，并且由于水文环境的变化，固定的水声信道也会存在时变，影响了这一方法的应用效果。文献[11]在声屏蔽基础上引入了旁瓣消除技术进一步提高直达波抑制效果，但存在与文献[10]相同的应用局限性。

综上所述，复杂时变的水声信道和主动声呐中直达波与回波间的强相干性，是直达波抑制技术所面临的主要困难。现有的直达波抑制方法针对以上问题进行了一系列的设计和改进工作，但是仍然存在一些方法上的不足或者应用条件受限的情形。

考虑到主动声呐中，发射波形信息是已知的，可以利用已知的发射信号波形设计匹配滤波器直接测量信道响应，然后利用信道响应重构直达波的波形，与接收信号中的直达波相减抵消，这样可以避免回波等有用信号被抵消。因此，直达波抑制问题可以转化为信道估计问题进行解决。

信道估计技术主要应用在无线通信中来消除码间串扰或获取分集增益。已有研究表明水声信道为稀疏信道，采用贪婪算法如匹配追踪(Matching pursuit,MP)、正交匹配追踪(Orthogonal matching pursuit,OMP) 等估计信道的稀疏结构，可以获得较高的估计精度[12−14]。常规的匹配追踪类算法在每一迭代中处理一个响应值，在信道稀疏度较高时(稀疏度>64)，需要反复计算接收信号与拷贝信号的互相关矩阵，这造成算法的收敛速度慢。为了提高跟踪效率，有学者提出了循环硬门限法(Iterative hard thresholding,IHT)[15]、分步匹配追踪算法(Stagewise orthogonal matching pursuit,StOMP)[16]等算法，可以根据设定阈值，一次跟踪多个响应值。但是IHT、StOMP等算法需要信号具备足够的带宽，来保证时延测量精度，一般用以处理高频信号。而低频主动声呐探测信号的带宽有限，这导致了这类改进算法在估计响应值时破坏了信道的稀疏性，降低了重构精度。为了满足实际应用需求，需要重新设计信道估计算法在提升重构效率的同时兼顾重构精度。

为了抑制双基地声呐中的直达波干扰，本文研究了通过测量信道响应重构直达波进行抵消的方法，并提出了一种通过动态因子控制阈值的匹配追踪算法，称为动态阈值匹配追踪(Dynamic thresholding matching pursuit,DTMP)算法，提高了重构波形抑制干扰的效率。与传统的OMP 算法相比，该算法可以在有限的迭代次数中快速收敛，减小运算时间；与StOMP 算法相比，在信号带宽有限的应用情形下，保证估计信道响应精度，避免过度重构导致回波波形被破坏的情形。仿真与海试处理结果都证明了该算法快速有效，具有实用价值。

1 直达波干扰重构抵消方法

本节利用浅海水声信道的模型，说明通过测量直达波信道响应，进行信号波形重构的原理。分析采用传统OMP算法和StOMP算法的局限性，介绍所提出的DTMP算法的原理，以及该算法在直达波抑制中的应用。

1.1 水声信道模型及直达波波形重构

直达波的传播信道可以采用抽头延迟线模型描述，信道的脉冲响应为

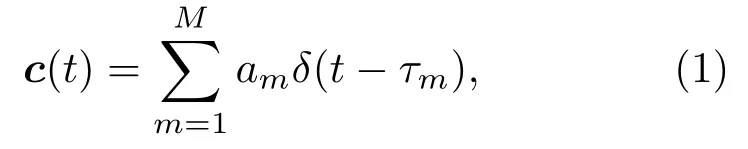
式(1)中，m表示路径的序号，共有M条路径，τm表示第m条路径的时延，am表示相应路径的响应强度。

如果主动探测中采用的带限信号为s(t)，经过浅海声信道后的直达波可以表示为

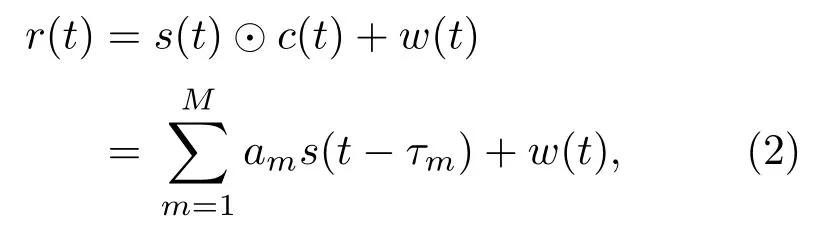
式(2)中的符号⊙表示卷积运算，w(t)表示背景噪声。

式(2)表明，信噪比足够高的情形下，通过测量信道响应c(t)并与发射的波形s(t)卷积，可以近似重构直达波波形，接收信号与重构波形相消，即可抑制直达波干扰，该过程的原理框图如图1所示。

图1 直达波波形重构抵消方法原理框图Fig.1 Schematic diagram of DBS based on waveform reconstruction

在主动声呐中，发射信号的波形s(t)是已知的，并且可以利用已知的发射信号波形信息，测量信道响应。由于水声信道具有稀疏性，信道估计器一般采用压缩感知类算法实现[14]。传统的OMP算法在信道估计中具有较高的精度，但是该算法每次迭代匹配一个最大响应值，在信道稀疏度较高时，需要反复计算接收信号与拷贝信号的互相关矩阵，运算量巨大，算法收敛速度慢。

为了提升收敛速度，所提出的IHT 算法、StOMP 等改进算法，需要信号有足够的带宽，保证较高的时延精度，才能有较好的重构效果。在低频主动声呐中，信号的带宽有限，限制了这类改进算法的应用。下面通过理论与算例简要分析带宽有限的低频信号限制上述算法应用效果的原因。带限信号的带宽为B，载频为fc，该频带内的信道响应可以表示为

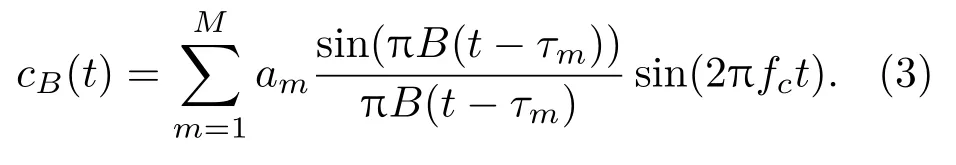
式(1)描述的信道冲击响应与式(3)描述的频带内sinc函数近似响应的包络如图2所示。

从式(3)描述的带通信道响应以及图2 可以看出，带宽有限信号进行匹配滤波或脉冲压缩处理后，时延分辨率有限(脉冲峰值宽度为1/B)，直接设置阈值提取的响应值破坏了信道的稀疏结构，降低了信道估计精度。以StOMP 算法和OMP 算法为例，阈值设置为1 时，两种算法在单次迭代中估计的信道响应结果如图3 所示。OMP 算法在单次迭代中搜索最大响应值，而StOMP 算法在单次迭代中会提取出所有超过阈值大小的响应值，实际是若干段的连续响应序列值。StOMP 的估计结果会导致重构的直达波信号失真，在抵消干扰的同时破坏了直达波以外的信号，尤其是回波信息。

图2 信道冲击响应与频带内近似响应Fig.2 The channel impulse response and its response in-band

图3 OMP 与StOMP 单次信道估计对比示意图Fig.3 Schematic diagram of channel estimation(single iteration) by OMP and StOMP

1.2 动态阈值匹配追踪

要想提升信道估计算法收敛速率的同时保证估计精度，关键是要估计每个信道响应值的准确位置。如果能够取出响应值的区间信息，在每个区间内检索最大值，就能克服信号带宽限制引起的时延精度不足所导致的估计性能受限的问题。该过程可以利用符号函数实现：依据预设的阈值将信号匹配滤波输出包络转换为符号序列；符号序列差分运算后可以得到多个响应值的区间信息；遍历每个区间，搜索最大响应值及其响应时刻，得到信道估计值。由此可以实现在单次迭代中准确估计多个响应值，保证估计精度的同时，提高收敛效率。另外需要注意的是，该实现过程，每一次迭代都需要设置一个合适的阈值，以有效提取响应值所在的区间信息。该阈值可以根据每次迭代中最大响应值，按照固定比例动态调整。基于以上思路，本文提出了DTMP算法。

下面给出DTMP算法估计信道响应、重构抵消干扰的处理流程：

算法初始时，设接收信号为r；拷贝信号为s，对拷贝信号补零使其与接收信号等长，进行Fourier变换后为S。设已进行的前p −1 次得到的响应值索引集合为Ip−1，信号残差为rp−1。

(1)在第p次迭代时，通过匹配滤波计算响应值。由于探测信号是带通信号，对响应幅值取包络，去除载波引起的周期性起伏，这可以提高后续操作中的时延估计精度：

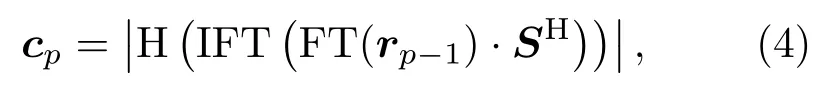
其中，运算符H(·)表示Hilbert 变换，FT(·)、IFT(·)表示Fourier 变换和反变换。进行频域变换的目的是为了提高计算互相关向量的效率。

(2)按照cp最大值的比例设定第p步的阈值Thresp：

其中，α为阈值的控制参数，其取值0<α1。运算符max(·)意为取最大值。

(3)将cp中的值按照选定阈值转化为符号函数：

式(6)将cp大于Thresp的值置1，小于Thresp的值置−1。

(4)对θp求导得到，具有以下性质：在cp大于Thresp区间的起始时刻值为+2，在结束时刻为−2，其余时刻的值恒为0。利用该性质分离得到所有可行区间的起始时刻和终止时刻：

其中，in+中的每个元素记录的是响应值所在区间的起始时刻，in−中的每个元素记录的是响应值所在区间的结束时刻；响应值对应区间[]内的最大值，角标k表示第k个区间，k= 1,2,···,K，K表示单次迭代中搜索到的所有响应值。

(5) 搜索所有K个区间内的最大值即可估计得到第p次迭代中的相干向量响应值与响应位置：

(6) 利用估计的索引集合构造第p次迭代的支持矩阵ΦJp={s(t −j)|j∈Jp}，并采用最小二乘法更新残差：

以上为DTMP 算法流程，算法终止时，可以近似认为残差中不包含直达波信号。

阈值控制参数α的取值对算法主要存在以下影响：α在1 附近取值时，DTMP 算法与OMP 算法等价；α取值过小会导致式(6)提取的有效区间数量过少，降低算法收敛速度，也会受到信号自相关旁瓣的影响产生估计误差。在应用中可以在0.4∼0.7间取值，具体参数根据直达波信号的自相关特性，以及接收信噪比设置：自相关旁瓣低、信噪比较高时，设置较小的α；自相关旁瓣高或信噪比较低时，设置较大的α值。

2 仿真分析与海试数据处理

本节对所提算法与OMP 以及StOMP 算法进行计算机仿真实验，对比3 种算法的收敛速度、干扰抑制效果以及波形信息保留效果等方面的性能。最后，再用3 种算法处理海试数据，对比3 种算法在试验环境中的性能差异，验证算法的实用性。

2.1 数值仿真分析

令信道扩展宽度M= 0.3 s，响应路径个数为K=8，每个路径的响应强度随机。信道冲击响应和带宽100 Hz 的响应的包络分别如图4(a)所示。仿真中设定阈值为1，利用式(5)、式(6)、式(7)中的方法，分割得到的区间示意图如图4(b)所示，红色线条是对符号函数差分的结果，该差分函数的非零时刻可以完整地描述响应值所在区间的起始时刻信息。在每个区间内搜索最大值，本次仿真中可以同时估计得到7个响应值。

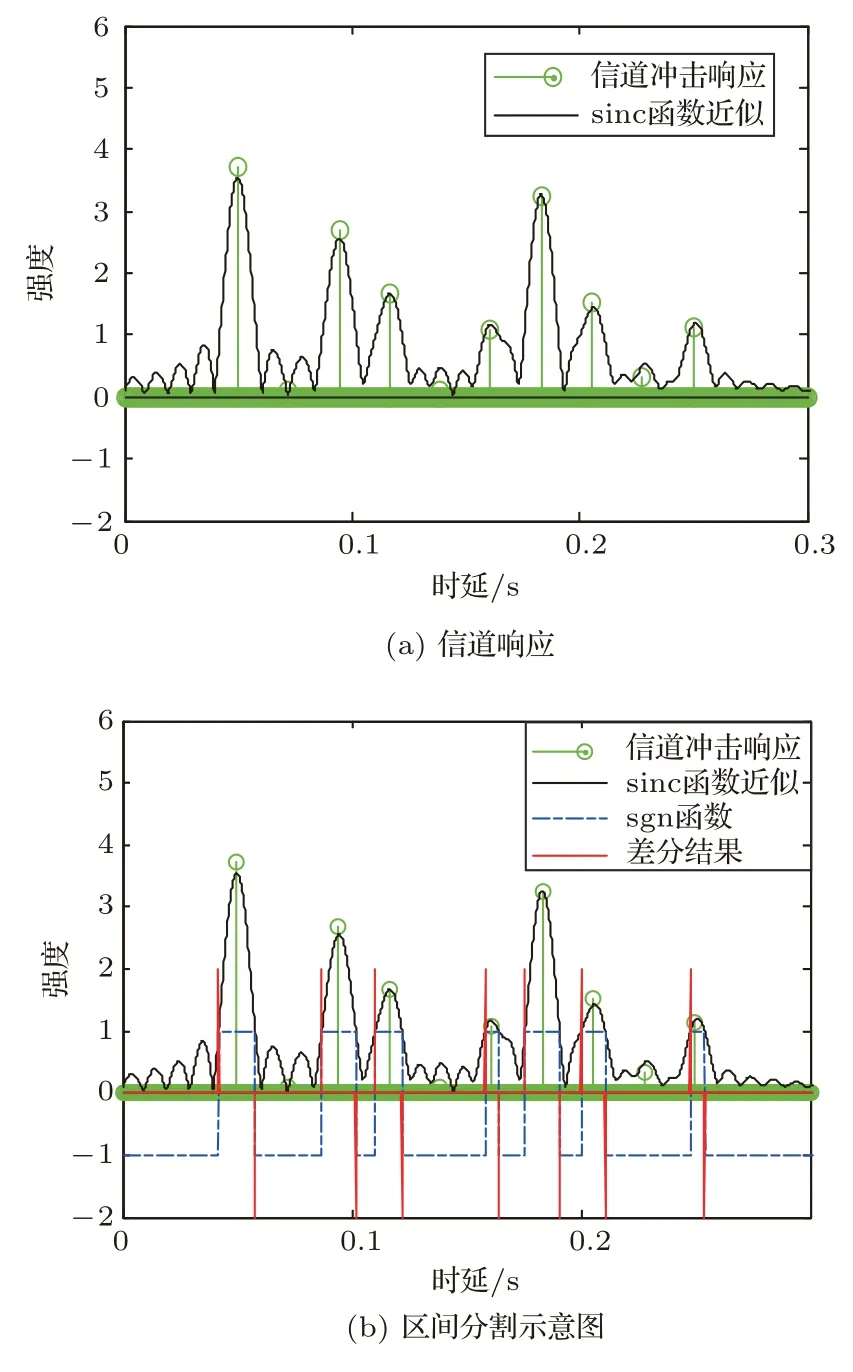
图4 信道响应及区间分割示意图Fig.4 Schematic diagram of channel response and interval grouping

接下来进行重构抵消仿真，验证所提算法在直达波抑制中的性能，并与既有方法做对比。采用声源信号为时长为18 s的伪随机信号，带宽为100 Hz；在声源信号后第4 s加入一段弱信号模拟回波，加入的信号与发射信号波形相同，根据声源信号能量强度设置加入信号的幅值为0.005，计算得到该情形下声源信号能量与模拟回波的能量相差约33 dB。由于伪随机信号的自相关主旁瓣比约为25 dB，因此模拟回波信号将被直达波信号完全掩蔽。图5(a)是仿真信号的波形情况，图5(b) 是分别将声源信号和模拟回波信号匹配滤波输出的结果，模拟回波信号的检测输出幅度为0.21，回波完全淹没在声源信号的旁瓣中。

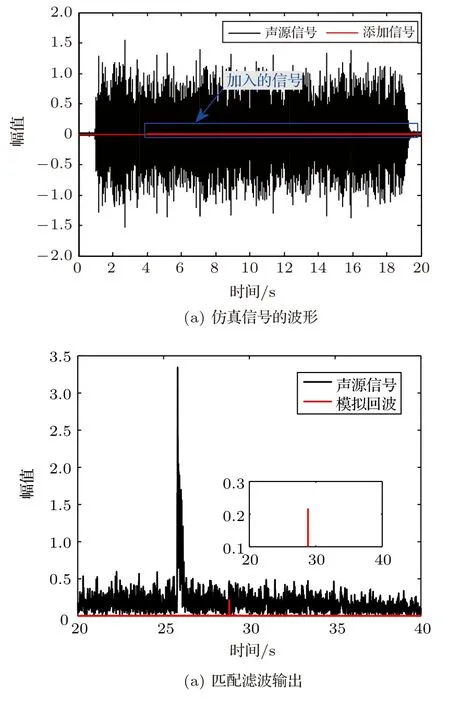
图5 仿真信号波形及匹配滤波输出Fig.5 Signal waveform in simulation and output of matched filter

分别采用OMP 算法、DTMP算法(α= 0.5)和StOMP 算法抵消直达波后进行匹配滤波并输出包络。图6(a)是OMP 算法迭代100 次后的重构抵消的结果，图6(b)是DTMP 算法迭代25 次后的处理的结果，图6(c)是StOMP 算法迭代25 次后的抵消结果。

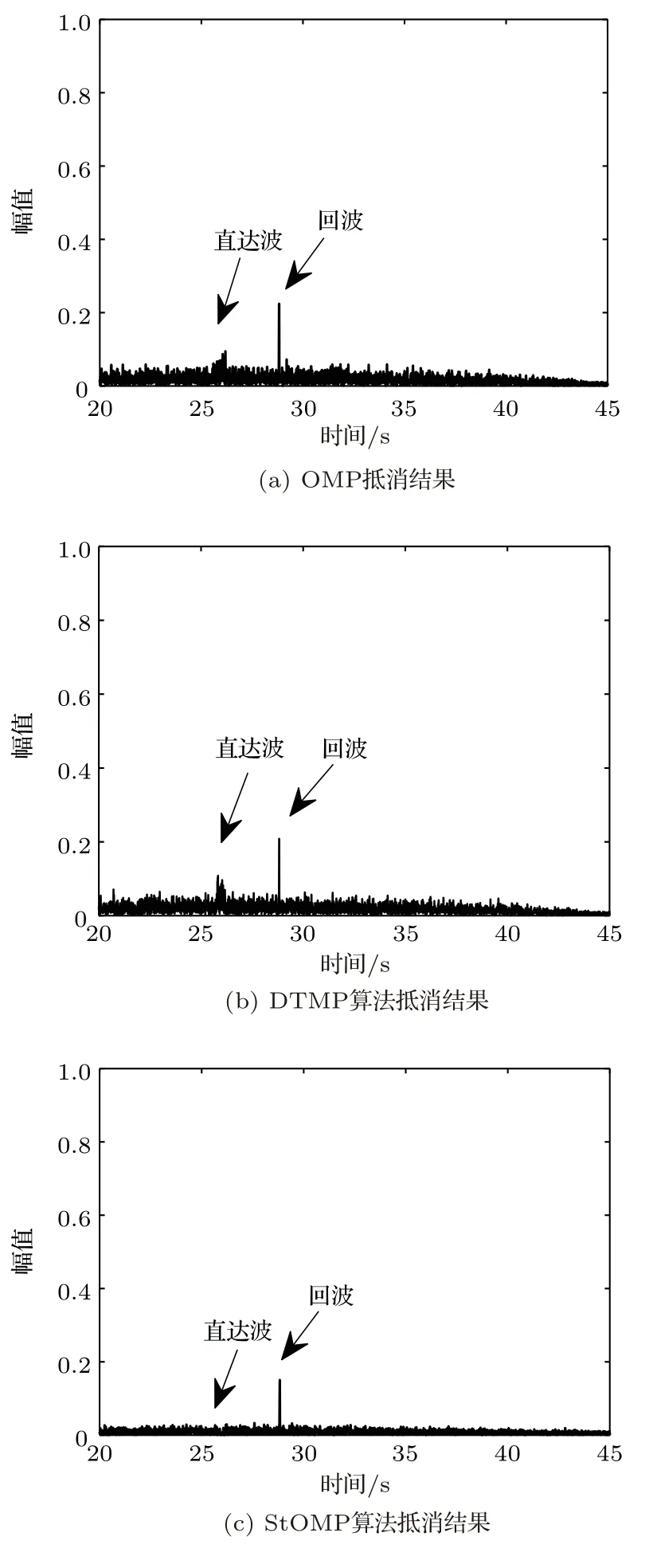
图6 直达波抑制后匹配滤波结果Fig.6 Result of matched filter after DBS

下面分析直达波抑制算法的性能，并以干扰抑制水平对比两种算法的性能差异。本文定义干扰抑制水平(Direct blast suppress level,DBSL)为

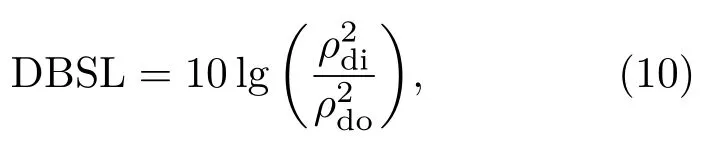
其中，ρdi为原始信号匹配滤波后的最大响应强度，ρdo为残差信号匹配滤波后的最大响应强度。

将本文提出的算法与传统的OMP 算法及其改进后的StOMP 算法进行对比。根据式(10)计算干扰抑制水平，OMP 算法为29.6 dB，DTMP 算法为28.7 dB，StOMP算法为33 dB。

分析算法保留回波信息的性能。回波损失水平(Echo loss,EL)定义为

其中，ρe是期望回波响应幅值，ρDBS是直达波抑制后的回波响应幅值。

仿真中期望响应幅值为0.21，OMP 算法的模拟回波响应幅值为0.197，DTMP 算法为0.194，StOMP算法为0.12。根据式(11)计算3种算法的回波损失水平，OMP 算法为−0.54 dB，DTMP 算法为−0.67 dB，StOMP 算法为−4.9 dB。对比发现，OMP 算法和DTMP 算法具有相近的抑制效果，两者的回波响应与期望回波响应相比几乎没有损失，较为理想地保留了回波信息；StOMP 算法虽然干扰波抑制水平更高，但是回波损失水平为−4.9 dB。表1是各算法的输出结果对比。

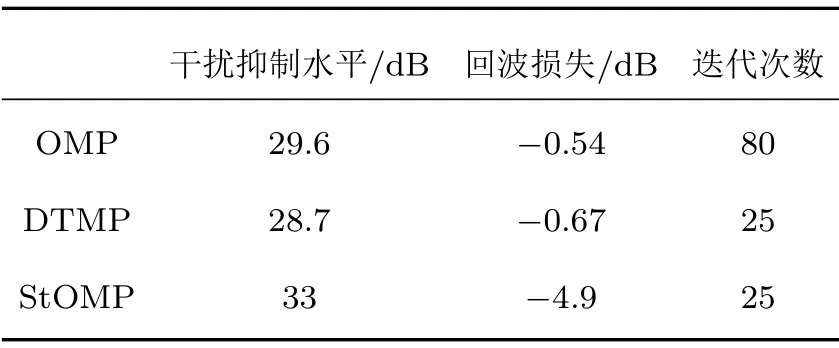
表1 算法仿真结果对比Table 1 Result of simulation

通过直达波响应估计结果进一步分析造成3 种算法性能差异的原因。图7 是3 种算法的信道估计结果，其中OMP算法和DTMP算法的估计结果，保持了良好的稀疏性，而StOMP 算法的估计结果是非稀疏的。实际直达波信道为稀疏的，因而StOMP算法估计的结果存在大量的冗余响应。这些冗余响应造成的估计偏差虽然能使信号的总能量衰减，但是由于与实际直达波信道响应失真，在抵消直达波信号的同时也破环了直达波以外的信号，造成了回波信号失真。

对比3种算法的收敛性能，图8是3种算法的迭代次数与信号残余能量的对比图。首先分析OMP算法和DTMP 算法，OMP算法和DTMP算法在迭代到一定次数时，信号的能量衰减趋于零。仿真实验条件下DTMP 算法迭代25 次即可有效收敛，而OMP 算法达到相近的抑制效果需要迭代100 次左右。由于匹配追踪类算法的计算量主要集中在互相关向量的计算上，通过每次迭代中跟踪多个向量，可以获得计算速度的提升。

StOMP 算法在经历快速衰减之后，信号的残余能量仍然会在每次迭代中小幅衰减，这种衰减实际是降低了信号整体的能量，会造成回波信号的损失。另外，由于StOMP算法估计的信道响应是非稀疏的，大量的冗余响应会降低算法的计算速度。

图7 直达波抑制前后波形对比Fig.7 Comparison diagram of channel estimation results

图8 OMP、DTMP 与StOMP 算法迭代次数对比Fig.8 Comparison diagram of OMP,DTMP,StOMP in iterations of convergence

2.2 海试数据处理

本小节对2018年4月在南中国海进行的主动探测实验获得的数据进行处理，验证直达波抵消算法的有效性。实验期间，信号发射船位于观测阵187◦方位，距离约10.2 km处；合作探测目标为一水面船，位于观测阵230◦方向，距离10.8 km 处，其相对方位如图9所示。实验中采用宽带伪随机信号，信号带宽为100 Hz，脉冲持续时间为18 s，这种信号具有很高的时延多普勒分辨力，但主旁瓣比为25 dB。实测数据中，直达波时延为6.7 s，理论回波时延约12.2 s，相对时延为5.5 s，而直达波时间长度为18 s，这在探测中形成了较长时间的直达波覆盖。

图9 直达波抑制前后匹配滤波结果Fig.9 Working location of trail ships

回波信号与直达波信号声传播损失相差约60 dB，由于采用的信号主旁瓣比值约为25 dB，波束形成、匹配滤波后的处理增益无法弥补由声传播损失引起的能量差异，需要进行直达波抑制。

分别采用OMP 算法、DTMP 算法和StOMP算法重构直达波信号抵消干扰。输出直达波抑制后的波形信息，对比3 种算法的性能差异。图10 是直达波抑制前后的时域波形对比，根据式(10)计算干扰3 种算法的抑制水平分别为33.9 dB、35.6 dB 和38.7 dB，仅从直达波干扰抑制水平上比较，OMP算法和DTMP 算法的抑制程度相当，StOMP 算法的抑制效果好于OMP算法和DTMP算法。从图10干扰抑制后的输出波形中很明显地可以看出这一点。

图11 是分别采用3 种算法处理数据时的收敛曲线。OMP 算法迭代80 次左右有效收敛，DTMP算法需要20 次左右，StOMP 算法迭代15 次左右有效收敛；OMP 算法和DTMP 算法的收敛曲线在快速收敛后趋于水平，而StOMP 算法则在快速收敛后，信号能量仍然随着迭代次数的继续减小。

图10 直达波抑制前后波形对比Fig.10 Waveform of direct blast before and after DBS

对未进行直达波抑制的阵列信号处理，进行常规波束形成后输出波形，进行多普勒补偿和匹配滤波得到的结果如图12(a)所示，回波信号完全淹没在直达波的旁瓣中。设置OMP算法迭代次数为80，DTMP 算法迭代次数为20，StOMP 算法迭代次数为15，直达波抑制处理后进行多普勒补偿并匹配滤波。对阵列数据处理，对每个通道接收的信号抑制直达波，阵列通道数量为60 通道。直达波抑制后的信号进行常规波束形成，获取阵增益，补偿多普勒后进行匹配滤波，输出结果如图12(b)、12(c)、12(d)所示。

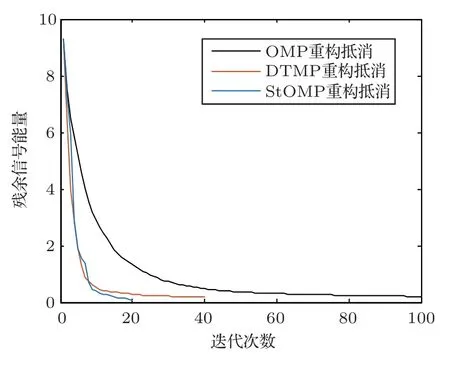
图11 OMP、DTMP 与StOMP 算法迭代次数对比Fig.11 Comparison diagram of OMP,DTMP,StOMP in iterations of convergence

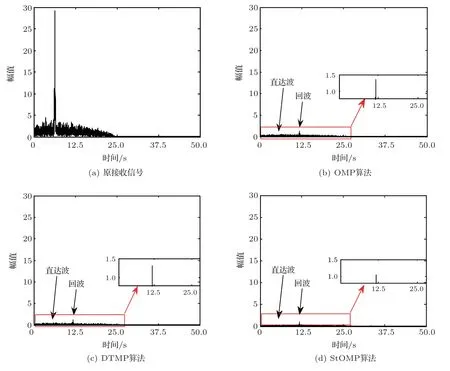
图12 直达波抑制前后匹配滤波结果Fig.12 Result of matched filter before and after DBS

对比3 种算法中的回波响应强度，OMP 算法的回波响应强度为1.37，DTMP算法的回波响应强度1.31，两者的回波响应强度接近；而StOMP 算法的回波响应强度为1.04，相比前两种算法，回波损失较为严重。实验环境中，无法获得回波的期望响应幅度，因此计算各算法间输出回波强度的比值。DTMP 算法输出结果与StOMP 算法的比值为2 dB，与OMP算法的输出结果的比值为−0.38 dB。对比后可以看出，在保留回波信息方面，DTMP 算法与OMP算法相近，优于StOMP算法。

回波检测结果说明，StOMP 算法输出结果中的干扰的能量虽然更低，但是由于信道估计结果存在失真，反而破坏了回波的波形，导致回波的处理增益存在严重损失；而OMP 算法和DTMP 算法估计的信道响应更接近直达波真实信道，在抑制直达波干扰的同时很好地保留了回波的信息，这与仿真中的结论吻合。海试数据处理结果说明了本文方法兼具抑制效果和收敛速度优势。

3 结论

针对双基地声呐中的直达波干扰，本文基于信号波形重构的思想，研究了通过估计直达波的信道响应重构直达波波形，对接收信号进行直达波抑制的方法，这种重构抵消算法几乎不影响直达波以外的信号。针对现有信道估计算法存在的问题，提出了一种DTMP算法估计直达波信道响应，兼顾重构精度和重构效率。数值仿真与海试数据处理结果表明与传统算法相比，所提算法在几乎不损失重构精度的情况下，大幅提高了直达波重构效率，有效地消除了双基地声呐中的直达波干扰，具有很强的实用价值。