基于路径选择的深海水下运动目标被动深度估计∗

刘炎堃 郭永刚 李整林 李风华 张 波

(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)

(2 中国科学院大学 北京 100049)

0 引言

深海水下运动目标被动定位一直是水声研究的重点内容之一。匹配场算法已在声源定位领域中获得了广泛应用，其基本原理是已知声速和海底深度等参数，对声场进行建模，通过比较测量场和拷贝场来对声源进行定位[1]。匹配场算法的分辨率受海洋水文、海底底质等环境参数影响[2]。当海洋的声速剖面未知时且信号记录时间足够长的情况下，McCargar 等[3]、Kniffin 等[4]基于深度的信号分离技术，可以利用直达波和海面反射波的信号相关结构来对声源定位；该方法使用了改进的傅里叶变换来还原目标的位置。Lei 等[5]利用布放在深海的两个水听器之间的互相关函数，对所有可能的位置进行扫描，使互相关函数值达到最大的位置即被视为是声源位置。匹配场技术和相关结构定位技术均需要两个或多个水听器同时进行工作，且需对空间进行扫描，往往有很大的计算量。

海洋声道的多径特性同样可以被用于定位声源。孙梅等[6]研究了在射线模型下，水平振速与垂直振速的传播损失与声线到达接收点处的掠射角以及收发水平距离之间的关系，分析了深海直达波区域声传播特性。王梦圆等[7]在此基础上，提出利用脉冲声信号的直达波和海面反射波的到达时延，研究了估计水下声源距离的方法。Gong 等[8]分析了使用拖曳水平阵进行被动目标定位的方法，并验证了卡尔曼滤波器方法对于运动声源的良好效果。Baggeroer等[9]与Duan等[10]研究了在深海可靠声路径中，位于临界深度以下的水听器可以在高信噪比的条件下接收到信号直达波和海面反射波，从而可以准确获得声传播的多径时延。Yang等[11−13]研究了在可靠声路径下，使用布设于深海的水听器或水听器阵列，利用直达波和海面反射波的到达时延和信噪比等信息对声源进行定位。在使用宽带信号时，仅仅使用单水听器就能通过自相关函数获得信号传播的时延信息；利用扩展卡尔曼算法，使用时延信息进行位置估计可以大大减少计算量[13]。然而在该方法中，定位算法需要先定义声源的初始状态，再进一步对声源进行定位算法的迭代。对声源的初始状态的定义不同将导致最后算法的定位效果的不同。

本文在多径时延算法[13]的基础上，提出了一种利用直达-海面反射波时延来对运动目标进行深度估计的算法，对声源可能的运动路径预先进行了选择，从而避免了对初始状态的定义，减少了需要的先验信息。对于每条运动路径，都可以看作是卡尔曼滤波的算法的观测输入，进而得到对运动的预测。通过比较预测位置的时延和理论计算出的时延，可以选择出最优的路径组，从而完成对目标深度的估计。

1 路径预选择与估计

根据射线模型，由声源位置到达接收位置的声线将经历水体折射和边界反射。图1 为从声源发出，到达间距为∆d的两个接收点的直达声线与海面反射声线的传播示意图。其中，S为声源点，S′为声源关于海面的镜像点；R1、R2为接收点。利用声线跟踪技术可以确定到达目标参考点的一系列特征声线。柱面坐标(r,z)系下的高斯射线方程[14]表示为

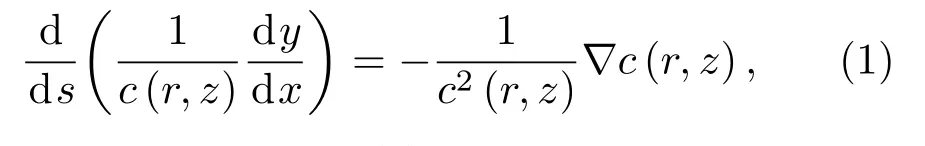
其中，r=r(s)及z=z(s)是射线的柱坐标，它们是弧长s的函数；c(r,z)为声速。设声线的曲率为p(s)，宽度为q(s)，单条高斯射线可以被表示为

其中，A为常数，n为与中心射线的垂直距离，ω为声源信号的角频率。τ(s)为传播时间即相位延迟，满足：

据此，可以从理论上得到射线的传播时间，从而计算出直达波和海面反射波之间到达时间的时延。

图1 声源-接收器声线示意图Fig.1 Schematic diagram of source-receiver acoustic rays

图2 为海深5500 m、位于深度4500 m 的水听器对应的仿真时延图，仿真中使用的是Munk 声速剖面。从图2 中可以看到，给定一个时延，有无数个可能的深度、距离与该时延值对应，这些深度、距离形成的位置组成了一条时延线；整个时延图呈现出明显的随深度变化的趋势。当声源目标运动时，水听器能接收到一系列的直达、海面反射波信号，从而可以计算得到一系列的时延线。每条时延线可以看作是所有点的一个子集，一个可能的路径可以看作是在n条时延线上的点的连线；每条路径都可以看作是时延线之间的一条连线，对运动路径的预选择即寻找可能表示目标运动的连线，这可以通过动态规划的方法实现。

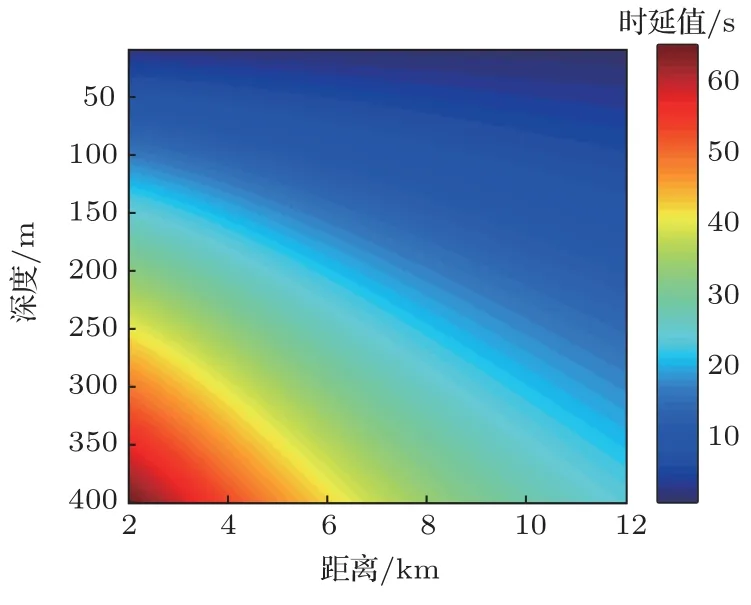
图2 水听器对应的直达-海面反射波时延图Fig.2 Time-delay map of direct-to-surface reflection waves for hydrophones

1.1 路径的预选择

为了确定所有时延线之间的连线中哪些可以更好地表示目标的运动，假设某个由N条时延线组成的路径为S，定义代价函数如下：

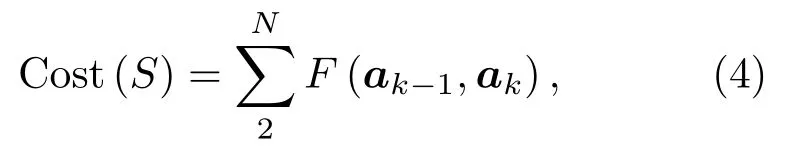
其中，Cost(S)为路径S的代价函数，ak为包含一个点的距离Rk、深度Dk和速度vk的矩阵，即

其中，、分别为在ak状态下的水平、垂直速度。函数F(ak−1,ak)为ak−1和ak两个点之间的代价。为了限制运动的速度、方向变化，函数F(ak−1,ak)定义如下：

其中，F(ak−1,ak)中的第一项α|vk−1−vk|2是对速度矢量变化的限制，而第二项是对垂直方向位移的限制。参数α和β体现了对目标运动的大致推测：α设置的越大，趋于匀速的连线代价越小；β设置的越大，趋于水平的连线代价越小。这样设置的目的是为了让路径趋于水平、匀速运动的路径，以模拟真实的目标运动。

假设已经获取了M个时延，对应在时延图上有着M个点集。设每个点集Am(m=1,2,···,M)上都有N个点，记为Am,km(km=1,2,···,N)。设以Am,km为终点的路径为Sm,km，Sm,km上的所有的点可以表示为从m个点集上各取一个点后所形成的集合：

则代价函数的计算可以表示为

涉身的含义是什么？莱考夫涉身心智观中的“‘涉身’是指人类‘依据生物性的能力以及身体与社会经验在外部环境中运作’，‘心智’则包括理性与概念，因此心智涉身性就是指人类理性和概念的建构都是涉身的，它们通过人类身体、大脑以及与外部世界的互动式运作而形成。”[3]30

公式(8)显示了每一个以Am,km为终点的候补路径的代价函数计算都仅与以前一个点集中的点为终点的候补路径代价函数Cost(Sm−1,km−1)(km−1= 1,2,···,N)有关。至此，对于任意的km(km= 1,2,···,N)，都可以在O(N)的时间内计算出Cost(Sm,km)。在深度上均匀选取q条候选路径进行运动估计。q越大，路径越密集，深度分辨率越高；q越小，路径越稀疏，深度分辨率越低。在实际实验中，q被设置为50，路径终点之间的深度间隔约为3∼5 m。在计算代价函数时记录下该轮计算里的每一个点对应的上一轮计算中的点，即可直接回溯得到路径。在给定km时，回溯的公式如下：

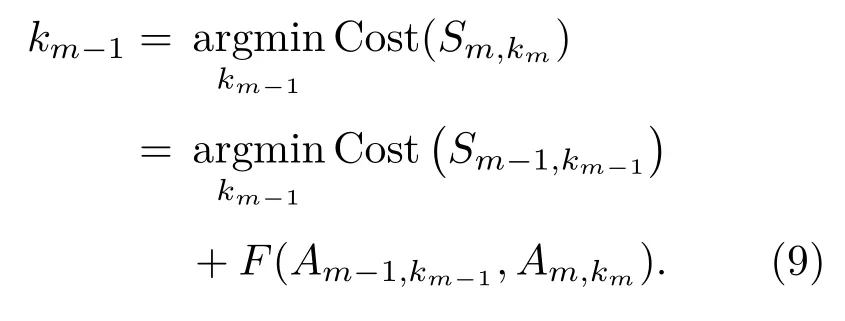
图3 为通过回溯计算后得到的部分候选路径，实际使用的候选路径均匀分布在选定的深度范围(从最浅的时延线深度到300 m)内，为了图片的清晰并未全部画出。计算路径代价的算法时间复杂度为O(MN)，路径回溯的算法时间复杂度为O(qM)。由于qN，O(qM)O(MN)，因此，路径的预选择算法的时间复杂度为O(MN)，和整个空间中点的个数呈线性关系，而当每次迭代更新路径时，需要的计算时间复杂度仅为O(N)。这种只与前一轮计算的结果相关的无后效性有利于减少大数据集和在线运算情况下的计算复杂度。

图3 由路径预选择算法得到的部分候选路径Fig.3 Candidate paths pre-selected by path choosing algorithm

1.2 基于卡尔曼滤波进行运动状态估计

卡尔曼滤波器是一种线性系统中高效的自回归滤波器[15]。在假设噪声为高斯过程的情况下，卡尔曼滤波可以给出满足最小均方误差的结果。由于选择的运动路径中的点是离散的，且运动可以看作是一个线性的系统，卡尔曼滤波器可以很好地对运动进行估计。

设状态向量为xk，xk的定义如下：

设状态对应的白噪声为ωk，则状态方程为

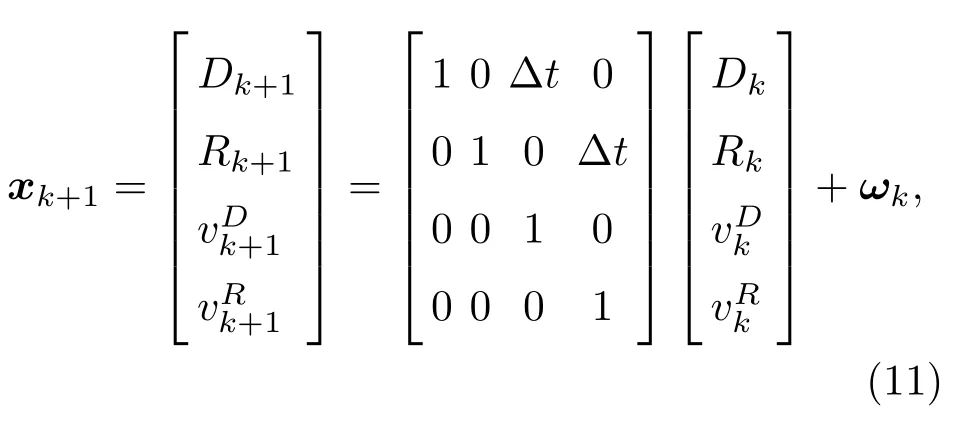
其中，∆t为接收到信号的时间间隔，ωk服从分布N(0,Q)，Q为状态误差的协方差为

其中，和为测量误差在深度和距离方向的标准差，B的值为

以每一个预选择路径上的点ak作为目标状态的观测，设测量误差为uk，则ak可以表示为

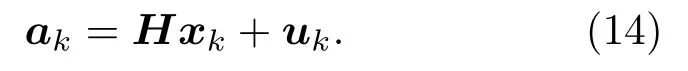
使用多条预选路径组成的集合P 来进行声源的深度估计。P 里的路径有着所有预选路径中最小的时延误差，即对于任意的p ∈P和qP，有

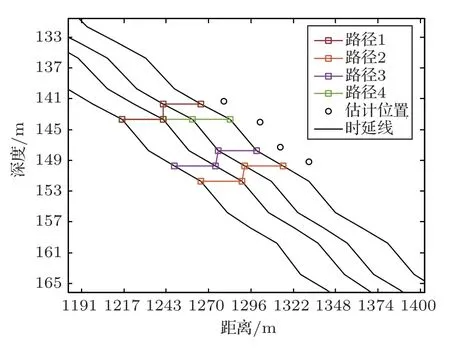
图4 卡尔曼滤波做运动估计示意图Fig.4 Schematic diagram of Kalman filter results

图5 算法流程图Fig.5 Algorithm flow chart

随着算法的进行，每一条预选路径在每接收到一个新的时延时都会进行伸展，向外扩展出一个新的点。对新的点使用方程(10)进行计算，会得到新的路径组。因此，每得到一个时延，都会对估计的深度进行一次迭代。完整的算法流程见图5。

2 实验介绍

实验的数据来自2018年春季在南中国海某次海上声学实验。实验采用单船结合接收阵垂直潜标的方式，接收阵为非均匀分布在120∼3408 m深度范围的24 阵元的水听器阵列，如图6 所示。实验过程中，实验船以大致3 n mile/h 的速度远离接收阵(图7)。拖曳换能器声源的深度大致保持在150 m左右，声源发射的信号中心频率为300 Hz，带宽为100 Hz。

图6 实验示意图Fig.6 Schematic of the experiment

实验过程中的距离水听器2 km∼35 km的海深分布如图8(a)所示，可见海底较为平坦，平均海深约为3300 m，接收水听器阵列所在海深为3500 m。计算使用的数据为船距离接收阵1.9 km∼9.6 km 的信号数据。实验期间测得的声速剖面见图8(b)。海底声学参数被设置为声速1565 m/s，密度1.6 g/cm3，吸收系数0.3 dB/λ[16]，用于本征声线的计算。图9 为基于声速剖面计算得到的深度位于3020 m、3370 m 的水听器的本征声线，可见声源到接收点的直达波和海面反射波的声线路径。在实验过程中使用同水听器固定在一起的压力传感器得到的位于2320 m、2370 m、3020 m、3370 m的水听器深度较稳定，可忽略接收深度变化的影响。在实验中对接收到的信号使用脉冲压缩方法进行截取。对4 个不同深度的水听器同一时刻接收到的信号处理如图10所示，可以看出信号到达的时间清晰的分为几组，与利用射线模型仿真的结果一致，其中，4 条线上起伏的幅度代表了脉冲压缩后的能量大小，直达波和一次海面反射的声波位于图10 中红色方框标示部分。直达波与海面反射波的到达时延值可以从接收信号的自相关函数的峰值中获得[13]。自相关函数的定义如下：

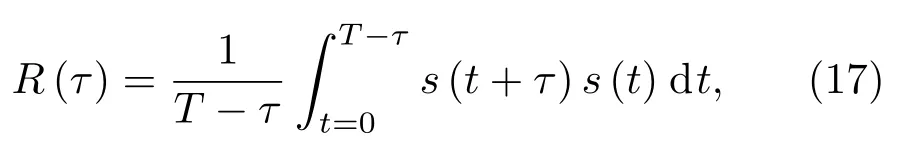
其中，T为选取的时间窗长，s(t)为接收信号。

图7 航行中“实验1 号”的速度变化Fig.7 Speed change of ship “Shiyan No.1”

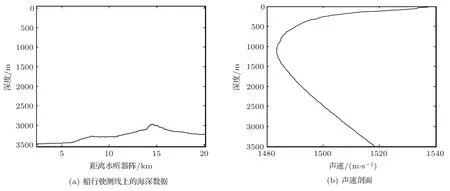
图8 实验测得海深及声速剖面Fig.8 Sea depth and sound profile

图9 不同接收深度的本征声线图Fig.9 Acoustic rays in different receiver depth

图10 4 个不同深度的潜标信号进行脉冲压缩后的结果Fig.10 Pulse compression of four submersible signals at different depths

利用声速剖面，预先计算得到2320 m、2370 m、3020 m、3370 m 深的水听器对应的直达波与海面反射波的时延图，参见图11。获得接收信号时延之后，即可对不同深度的水听器在图11上寻找对应的时延线。根据接收信号中得到的时延信息，利用公式(9)计算获得路径，并将路径看作是卡尔曼滤波的一次观测进行运动估计。将运动估计的结果与预先计算的时延图中进行比对，可以得到最接近的路径，从而迭代一次估计的声源深度。在迭代的过程中，不同深度的水听器接收到的信号在计算上是完全独立的。由于少数时延值不一定能获取到稳定的最优路径组，在第一次迭代之前预先使用了10 个时延值进行了路径选择算法。

图12 为实验中使用的各个深度水听器信号中得到的前40个时延值。从图12中可以看出，随着声源逐渐远离水听器阵，各水听器接收到的直达波和海面反射波之间的时延值逐渐下降，且越深的水听器对应的时延值越高，与图11一致。其中，由于噪声干扰，位于2370 m的水听器计算时延值出现了错误的峰值的情况，使时延值曲线产生了较大起伏。

图11 不同接收深度下的直达波与海面反射波的时延图Fig.11 Time delay map of direct waves and sea reflections under different receiver depth

图12 使用互相关得到的实验中各深度水听器前40 个时延值Fig.12 The first 40 delay values of each depth hydrophone in the experiment using cross correlation

图13 比较了用线性插值替换异常的时延值与异常时延值对应的时延线，可见异常值将导致目标可能的位置出现偏差，使路径产生一定程度的畸变，导致公式(8)定义的代价函数值突增。图14展示了算法对实验数据进行深度估计的结果。图14(a)为单独使用某个水听器的数据计算的深度迭代图，其中蓝色带星号的曲线是由与拖曳声源固定在一起的测深仪提供的深度数据；从图14(a)可以看到，当使用深度位于2320 m、3020 m、3370 m处的水听器接收到的信号进行声源深度估计时，估计的相对误差大致在10%以内。使用深度为2370 m 的水听器接收到信号进行深度估计时，由于时延数据的不准确，迭代初期的最优路径选择并不稳定，估计深度变化较大，导致在前20次深度迭代总深度估计的误差大，最大值为第一次估计，相对误差的绝对值达到70%；在第23 次迭代后，深度估计的误差下降到了15%以内。去除异常的时延值后，2370 m 深水听器的深度估计曲线见图14(b)。图14(b)说明在时延值计算出现较大误差时，将使估计的深度变得不准确；而后在时延值计算准确时，2370 m 深水听器的深度估计结果误差变小。因此，计算过程中可以在每次迭代前预先抛弃一定迭代次数以前的时延值来进行下一步计算，避免原异常数据对后续计算的影响。利用4 个水听器的数据同时对目标深度进行估计，把每次估计迭代中代价函数值最低的前5 个深度都统计进结果中，则深度估计呈现的离散序列针状图见图15。图15 中每一列的深度宽度范围为5 m。由于直达波与海面反射波的时延在时延图上对应的是一条线，在数据量少的时候可能出现深度偏差比较大的估计。在图15中，深度位于区间[0 m,100 m]和[200 m,300 m]的估计点数约占所有点数的25.9%。对整个估计的离散点序列进行高斯曲线拟合：

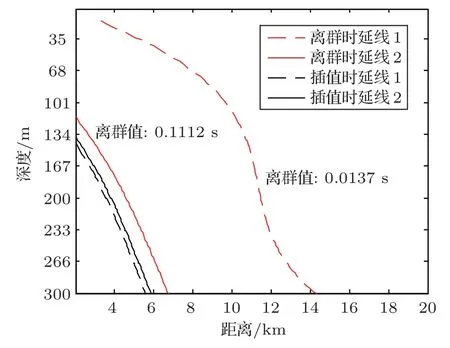
图13 2370 m 水听器的时延异常值产生的时延线偏移Fig.13 Time delay line offset due to the outliers value of 2370 m hydrophone

图14 深度估计结果Fig.14 Depth estimation results

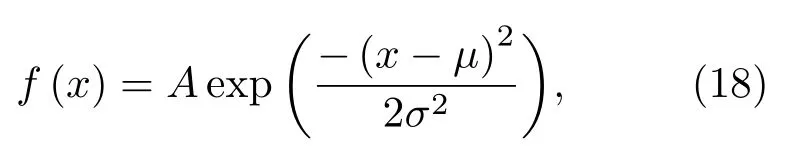
得到的置信水平在95%下的拟合参数见表1。从曲线的拟合结果来看，多次迭代中对声源运动中的深度估计值大致分布在真实深度的附近，分布的均值为145.8 m。

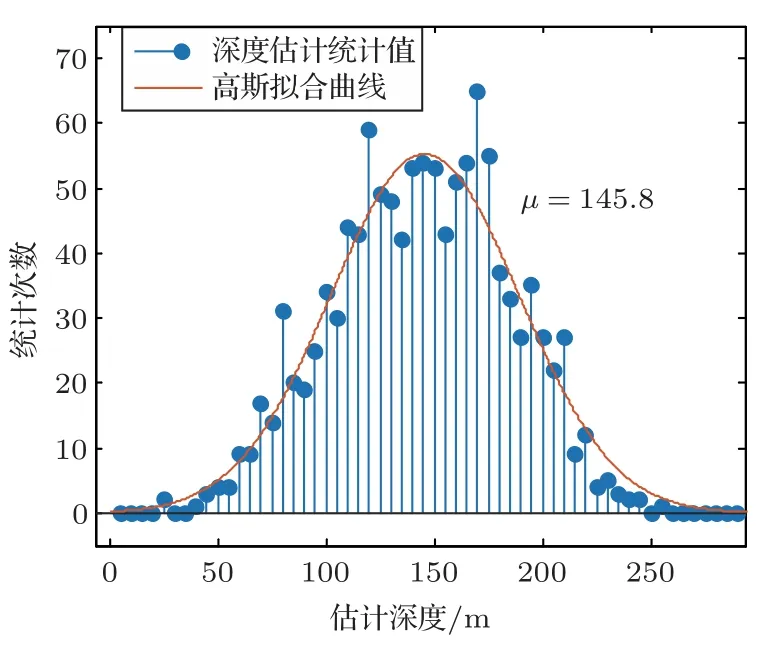
图15 各水听器每次估计中代价值前五的深度统计结果Fig.15 Statistical results of hydrophones in top five depth estimation

表1 置信水平为95% 的深度估计曲线拟合参数Table 1 Curve fitting parameters for depth estimation with a confidence level of 95%

3 结论

本文提出了一种基于单水听器进行水下运动目标深度估计方法。利用直达-海面反射波时延预先构建出候选运动路径，避免了对目标初始状态的定义；使用候选路径对目标运动的轨迹进行模拟，从而实现了对目标的深度估计。使用候选路径的方法可以避免每次迭代在整个空间进行搜索，减少了计算复杂度。实验结果验证了该方法的有效性。由于需要获取信号的到达时延值，该算法仅适用于深海直达声区。若运动目标在深度或运动速度大小上变化较大，将导致路径选择算法的失效，后续研究将进一步分析路径选择对最终深度估计的影响。致谢 感谢参与2018年4月南中国海调查全体实验人员，他们的辛勤劳动为本文提供了珍贵可靠的实验数据。