双细胞光声信号的有限元分析∗
赵荣荣 杨 鹏 韩建宁
(中北大学信息与通信工程学院 太原 030051)
0 引言
光声检测作为一种高分辨率无标签的光学成像技术,结合了光学成像的高对比度和声学成像的深度,可实现对处于自然状态的生物粒子形态进行无损伤测量,近年来发展迅速。光声成像的本质是光声效应,脉冲激光照射生物颗粒,生物颗粒由于吸收光能而温度升高,体积发生膨胀和缩小,产生声波,通过分析声波,得到生物粒子的相关信息,细胞的频域声压级曲线可用于评估细胞大小和形态等特征,作为疾病早期诊断的一种有前景的手段。红细胞(Erythrocyte/red blood cell,RBC)中的血红蛋白,凭借较高的光吸收系数,成为体内光声成像的理想内源性造影剂[1]。根据红细胞的频域声压级曲线可以得到红细胞的尺寸和形态等信息。细胞的形状和功能之间有着密切的关系,因而细胞和细胞器形态的光声测量,为了解细胞功能和疾病诊断提供重要的信息。
文献[2]通过单细胞的频域声压级曲线,可以实现对单个红细胞的大小和形态的检测,对正常细胞与异形细胞进行定性鉴别。文献[3]研究了红细胞聚集体,用光声信号的参数评估人体血液中红细胞的聚集水平。然而,前者研究的对象是单个细胞,后者的研究对象是细胞聚集体,讨论的内容是光声信号与细胞聚集程度的关系,并没有关注细胞间光声信号的相互影响。所以,一个细胞对另一个细胞在不同距离下的影响还没有被关注。
人体内正常红细胞的存在状态是游离的单个细胞,但细胞之间距离较近,信号会相互影响和干扰,且细胞间的距离是随机的。在一项研究中[2],提出了一种光声快速定量单个红细胞形态变化的方法,此方法比电阻抗和光散射方法更准确,比血液涂片和光学干涉方法更快速简便。这项研究表明,不同大小、形状、取向和成分的红细胞,在100 MHz 以上的光声光谱中观察到独特的周期性变化的最小值和最大值,但是研究只提及光声成像在测量大量样本上的潜力,并没有进一步分析多细胞条件下的单细胞检测情况。本文的目的是补充和拓展单细胞光声检测的内容,讨论距离对细胞光声信号的影响,找到细胞间相互影响最小的距离。
1 分析方法
1.1 方法介绍
为了能够在两个细胞的光声信号相互影响的条件下,通过调节细胞间的距离,获得相互干扰最小的光声信号,本文对单细胞和不同距离的双细胞进行有限元分析,研究建立了单细胞信号模型和不同距离的双细胞信号模型。在理论模型中,一个红细胞位于球形水环境的中心,称其为主体红细胞,另一个相同细胞位于其正上方,以400 MHz 的频率计算单位波长,按照波长的倍数设置上方红细胞与主体红细胞的距离,得到了不同距离下主体红细胞不同角度的频域声压级曲线。另外,通过单细胞信号模型,计算出了没有上方红细胞干扰时,单个红细胞不同角度的频域声压级曲线。
判断曲线相似性的方法主要有特征值法和相似性函数定义法。特征值法是对曲线特征参数进行比较来度量两个曲线的相似性,而相似性函数定义法是比较两个曲线之间的距离来度量两个曲线的相似性,相似性函数定义法在比较两条曲线形状的相似性上优于特征值法。不同距离下红细胞的频域声压级曲线振幅相差不大,差异主要体现在曲线的斜率上,于是本文选择了基于形状判断曲线相似性的离散frechet 距离的方法。基于离散frechet 距离的方法,以45◦位置为例,通过frechet 数值度量细胞频域声压级曲线的相似性,且假设frechet数值越小,相似性越高[4]。结果表明,frechet 数值最小的曲线与观察得到的最相似的曲线是同一条曲线,即frechet 数值可以很好地度量频域声压级曲线的相似性。
1.2 参数设置
本文利用COMSOL Multiphysics 实现了细胞的有限元分析,以检测两个红细胞在不同距离下的光声信号。研究建立了二维轴对称模型,相比于三维模型,二维模型的计算量更小,且能产生有效的结果[5−7]。利用基本图形的组合和分割,得到了双凹形红细胞几何模型。同时,添加了压力声学瞬态物理场,建立了全局笛卡尔坐标系。
正常红细胞的形状是双凹形的圆饼状,中间两面微凹,边缘较厚。红细胞平均直径约为7.8 µm,高为1∼2 µm,体积为94 µm3。本文的理论模型是由Evans 等[8]开发的模型(双凹形细胞位于10 µm 半径球形系统)扩展得到。根据红细胞的几何物理参数,确定了红细胞模型的几何形状,模型中的红细胞直径确定为7.82 µm,双凹形细胞处于圆形的水环境中。为了进行有限元分析,将细胞模型的几何形状划分成自由剖分三角形网格,采用网格尺寸为标准。

表1 模型参数Table 1 Model parameters
在以往的研究中,已经找到了红细胞的最佳光吸收的激光束的波长,在血液样本中,红细胞可以被看作是入射光的主要吸收体和光声信号的主要辐射源[9]。因此,本研究将细胞和水环境设置为理想状态,只将红细胞作为入射光辐射的吸收体和光声信号辐射源,忽略外围水对入射光的吸收和光声信号的对外辐射,且红细胞均匀吸收激光。激光束照射之前,细胞的初始压力值为0 Pa,水的初始压力值为0 Pa,激光束照射之后,细胞的初始压力值为1 Pa,水的初始压力值为0 Pa。红细胞内的质量密度和声速分别为1110 kg/m3和1650 m/s,与先前研究中测量的数据一致[10−11]。细胞外围水环境的质量密度和声速分别为1000 kg/m3和1520 m/s。模型参数设置如表1 所示。时域的检测范围是0∼10 ns,频域的检测范围是0∼1000 MHz,数据由COMSOL Multiphysics生成,数据的后处理由MATLAB R2014a完成。
1.3 单个红细胞模型
在二维仿真模型中,以(0,0)点为圆心,以90 µm 为半径,建立了水环境,红细胞处于水环境中。如图1(a)所示,双凹形红细胞处于圆形水环境的中心,在细胞的一侧设置探测点。细胞模拟图是细胞的侧视图,在侧视图中,建立直角坐标系,设置水平的X轴和垂直的Y轴,X轴是细胞长直径的方向,Y轴是细胞的厚度方向,且红细胞的中心与圆形水环境的中心相互重合,x轴和y轴是主体红细胞的对称轴。红细胞的尺寸和取向是影响单个红细胞的光谱特征的因素,于是,选择直径为7.82 µm的双凹形红细胞平置于圆形水环境的中心。
图1(b)是水环境中的细胞部分放大图,以细胞中心为圆心,建立极坐标系,以10 µm 为半径,以−75◦∼75◦为范围,每隔15◦布置一个探测点,检测红细胞的频域声压级曲线。声压是大气压受到声波扰动后产生的变化,在大气压强上的叠加一个声波扰动引起的压强变化,通过声压可以描述光声信号的传播情况。声压级定义为被测光声信号的声压与基准参考声压之比取以10为底的对数再乘以20,单位是分贝(dB)。

图1 单细胞二维模型Fig.1 Single cell two-dimensional model
图2 分别是单个细胞0◦∼75◦、−15◦∼−75◦的时域声压分布,通过观察,由于曲线间重叠严重,很难得到曲线的相关规律,也难以得到细胞的形态特征。但是细胞的频域声压级分布通过周期性变化的极大值和极小值来反映细胞的形态特征[12]。于是,对不同角度采集到的时域声压信号进行傅里叶变换,得到频域声压级分布[13]。
图3 分别是单个红细胞0◦∼75◦、−15◦∼−75◦的频域声压级分布。探测点的角度不同,检测到的频域声压级曲线有着明显的不同。观察图3(a)和图3(b),对比曲线15◦与−15◦、30◦与−30◦、45◦与−45◦、60◦与−60◦、75◦与−75◦,发现它们有着较高的相似度,这是因为单个红细胞的形状关于x轴对称。但是,完全重合的部分大约是在0∼500 MHz,超出500 MHz的范围出现一些差异,这是由于声波的散射。声波的频率越高,波长越短,个别分子或原子的运动会影响声波,且频率越高,散射越强,导致在较高频率时,对称探测位置的仿真曲线不重合。
这里只分析从0◦∼75◦的频域声压级曲线分布情况。在0◦方向,大约从200 MHz开始,出现周期性变化的最小值和最大值。在75◦方向,整个频谱只在800 MHz 左右出现了最小值。在15◦、30◦、45◦、60◦方向,大约分别从220 MHz、250 MHz、350 MHz、450 MHz开始,出现周期性变化的最小值和最大值。可以发现,从0◦∼75◦,开始出现最小值的位置在x轴上不断后移,在200 MHz∼800 MHz 之间依次分布,且每条曲线的最小值之间的距离在不断增大。在单个细胞的光声频谱中,0◦位置可以观察到最多的最小值点,75◦位置观察到最少的最小值点。同时,在这些曲线的第一个最小值(200 MHz)出现前,从0◦∼75◦,曲线的振幅在不断地增大。

图2 单个红细胞时域声压分布Fig.2 Time domain sound pressure distribution of a single RBC

图3 单个红细胞频域声压级分布Fig.3 Sound pressure level distribution in frequency domain of a single RBC
1.4 不同距离的两个红细胞模型
在单个红细胞模型的基础上,以中心的红细胞为主体红细胞,添加另一个红细胞。在本研究中,为了使细胞间的距离作为影响主体红细胞光声特征的唯一因素,需要将主体红细胞的尺寸及取向和另一个红细胞设置为相同状态。主体红细胞处于圆形水环境的圆心。另一个红细胞处于主体红细胞上方正对位置,其中心在y轴上。主体红细胞在水环境中的位置固定,通过控制另一个细胞在y轴上位置,调节两个细胞之间的距离,且两个细胞的距离是两个细胞中心之间的距离。如图4(a)所示,是处于圆形水环境中两个细胞距离为19 µm时的二维模型图。
利用波的干涉原理,即两个相同的波源,它们的两列波叠加,在传播区域会形成稳定的加强区和稳定的减弱区,加强区与减弱区相间分布,以此来调节两个细胞之间的距离,使探测点的位置尽可能多地设置在加强区,使探测的光声信号干扰最小。观察图3(a)和图3(b) 可以发现,单个红细胞的光声频谱在频率是400 MHz 时,几乎各个角度光谱振幅处于最大值或者最大值的附近,同时也表明,红细胞的光声频谱信息在400 MHz 时最为丰富。细胞的光声信号在37◦C 水中传播,水在37◦C 的声速是1520 m/s,根据频率与波长的关系可知,400 MHz 的波长为3.8 µm。以3.8 µm 为单位,设置11组不同距离,分别是2.85µm(3/4波长)、3.8 µm、7.6 µm、11.4 µm、15.2 µm、19µm、22.8 µm、26.6 µm、30.4 µm、34.2 µm、38 µm。同样,与单个红细胞探测点的设置相同,以10 µm 为半径,以−75◦∼75◦为范围,每隔15◦布置一个探测点,如图4(b)所示,描述了两个细胞在距离为19 µm 时的相关设置。这样,可以得到主体红细胞在与另一个红细胞不同距离时,各个角度的探测点的光声信号。

图4 双细胞二维模型Fig.4 Two-cell two-dimensional model
2 分析结果
以主体红细胞45◦位置探测点的频域声压级曲线为例,演示了在11 个不同的距离下,寻找与单个红细胞最相似的曲线的过程,并进行了效果对比。图5(a)是主体红细胞在45◦位置下,距离为3/4λ ∼4λ的频域声压级曲线,将单个主体红细胞与6 个不同距离下的频域声压级曲线进行对比。图5(b)是主体红细胞在45◦位置下,距离为5λ ∼10λ的频域声压级曲线,将单个主体红细胞与5 个不同距离下的频域声压级曲线进行对比。对比图5(a)和图5(b)可以发现,图5(b)中有更多的曲线与红色的单细胞曲线相似与重合,说明细胞间相互影响最小的距离,分布在5λ∼10λ的可能性更高。
进行频域声压级曲线的定量分析时,主要尺度是曲线的振幅和斜率。根据图5(a)和图5(b) 可得,在26.6 µm距离下的曲线与单个红细胞的曲线相似度最高,不论是振幅还是斜率都有着极高的相似度,两个曲线几乎重合,如图6(a)所示,是主体红细胞在45◦位置下,距离为26.6 µm 的曲线与单个红细胞45◦位置的曲线进行比较的结果。

图5 45◦位置不同距离与单细胞比较Fig.5 The different distances and at 45◦position compared with single cells

图6 45◦位置最佳相似比较结果Fig.6 The best similarity comparison results of 45◦position
图6(b)是主体红细胞在45◦位置时,不同距离下的频域声压级曲线与单个红细胞的曲线进行比较,得到的frechet 数值。此时,假设frechet 数值越小,相似度越高,通过观察单个红细胞在45◦时的曲线与不同距离下主体红细胞45◦位置的曲线的相似程度,判断假设是否正确。由图6(b)可得,在26.6 µm 的距离下,frechet 数值最小。结果表明,frechet 数值最小的距离正是曲线相似度最高的距离,frechet数值可以很好地度量光声曲线的相似度。
图7 是主体红细胞分别在0◦、15◦、30◦、60◦、75◦位置时的最佳相似对比的结果。主体红细胞的5 个位置执行与上述45◦位置相同的操作,即每个位置,将主体红细胞11 个不同距离的频域声压级曲线与单个红细胞同位置的频域声压级曲线对比,计算出11 个距离中frechet 数值最小的曲线,以曲线图的方式呈现单个红细胞同位置的频域声压级曲线与frechet数值最小的曲线对比的结果。
图7(a)是0◦位置单个红细胞与主体红细胞34.2 µm 距离的对比结果;图7(b) 是15◦位置单个红细胞与主体红细胞30.4 µm 距离的对比结果;图7(c)是30◦位置单个红细胞与主体红细胞26.6µm距离的对比结果;图7(d)是60◦位置单个红细胞与主体红细胞19 µm 距离的对比结果;图7(e)是75◦位置单个红细胞与主体红细胞26.6 µm 距离的对比结果。除60◦位置外,其他4 个位置曲线的重合度较高。
图8 是主体红细胞分别在−15◦、−30◦、−45◦、−60◦、−75◦位置时的最佳相似对比的结果。主体红细胞的5 个位置执行与上述45◦位置相同的操作,即每个位置,将主体红细胞11 个不同距离的频域声压级曲线与单个红细胞同位置的频域声压级曲线对比,计算出11 个距离中frechet 数值最小的曲线,以曲线图的方式呈现单个红细胞同位置的频域声压级曲线与frechet 数值最小的曲线对比的结果。图8(a)是−15◦位置单个红细胞与主体红细胞30.4 µm 距离的对比结果;图8(b)是−30◦位置单个红细胞与主体红细胞30.4 µm 距离的对比结果;图8(c)是−45◦位置单个红细胞与主体红细胞38 µm 距离的对比结果;图8(d)是−60◦位置单个红细胞与主体红细胞38 µm 距离的对比结果;图8(e)是−75◦位置单个红细胞与主体红细胞26.6 µm 距离的对比结果。除−60◦位置外,其他4个位置曲线的重合度较高。
在双细胞模型中,主体红细胞与另一个相同的细胞共有11 个不同的距离,每个距离下,有11 个不同角度的探测位置。将每个距离下的11 个角度的频域声压级曲线设置为一组,计算11 个角度的频域声压级曲线与同位置单个红细胞频域声压级曲线的frechet 数值,求取每组11 个角度的frechet 数值的均值。图9 是主体红细胞11 个距离下frechet数值的均值,随着距离的增大,frechet均值整体呈现先下降后上升的趋势,在26.6µm时达到最小值。即随着距离的增大,主体红细胞频域声压级曲线与单个红细胞同位置频域声压级曲线的相似度先增大后减小,在26.6 µm 处相似度达到最高。由此可得,双细胞模型中,两个细胞在26.6 µm 时,光声信号相互影响最小,且在30◦、45◦、75◦、−75◦位置达到最佳相似,有较高的相似度。
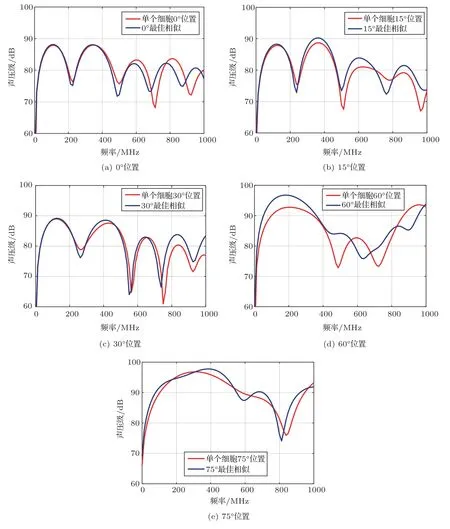
图7 0◦、15◦、30◦、60◦、75◦最佳相似对比Fig.7 The optimum similarity comparison of 0◦,15◦,30◦,60◦and 75◦

图8 −15◦、−30◦、−45◦、−60◦、−75◦最佳相似对比Fig.8 The optimum similarity comparison of −15◦, −30◦, −45◦, −60◦, −75◦

图9 不同距离下frechet 数值的均值Fig.9 Mean value of frechet values at different distances
3 结论与讨论
在先前的研究中,已经实现了光声快速定量单个红细胞的形态,但是没有进一步讨论在多细胞条件下如何检测单细胞的光声信号,即没有考虑细胞信号之间的相互影响。而且,对光声谱进行定量分析时,采用的方法是分析光声谱中某频率的振幅和某段频率的斜率,只提取了光声谱的部分信息,适用于被测细胞的形状有较大差异的情况。为此,本文讨论了两个红细胞在不同距离下光声信号之间的影响。对单个红细胞和不同距离的两个红细胞进行了有限元分析。以圆形水环境中心的红细胞为主体红细胞,在主体红细胞右侧的不同角度布置探测点,调整另一个红细胞与主体红细胞的距离,计算得到主体红细胞不同距离不同角度下的频域声压级曲线。引入frechet 距离来度量曲线的相似性,分析全部频率段,量化曲线间的细微差异,将frechet 距离作为分析光声曲线有力的工具。利用frechet数值来度量两条光声曲线的相似性,frechet 数值越小,两条曲线越相似。其中,计算细胞间信号的相互影响,使用相似性函数定义法度量光声曲线的相似性,在以往的研究中还没有被讨论过。
当主体红细胞的检测角度一定时,在不同距离的主体红细胞的光声曲线中,存在frechet 数值最小的曲线,即这条曲线是此角度下的最佳相似曲线。同样,观察可得,当两个细胞距离为26.6 µm时,11 个角度的frechet 数值的均值最小,曲线相似度最高。
本文的实验原理是声波干涉,这种方法不仅可以应用于红细胞,几乎任何含有内源性和外源性造影剂的细胞,都可以通过此方法找到细胞间光声信号干扰最小的距离。由于实验条件的限制,本文研究的背景为体外检测,首先讨论了两个相同红细胞之间光声信号的相互影响,再次,将研究多个不同细胞之间光声信号的相互影响,最终实现体外同时检测多个不同细胞的光声信号的目标,目的是补充和拓展光声显微技术中多细胞光声检测的内容。

