斜坡海底波导中随机声源的信道盲解卷积∗

张雪冬 牛海强 吴立新

(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)

(2 中国科学院大学 北京 100049)

0 引言

水下声源和接收阵之间的信道脉冲响应(Channel impulse response,CIR，也称为格林函数)在海洋声学研究中有重要的作用[1]。信道响应的估计有基于主动信号和被动信号两种方法。基于主动信号的方法用已知的声源发射的信号对接收信号数据进行解卷积来估计信道响应，这种方法得到的信道响应比较精确，缺点是需要预先知道声源的频谱信息。基于被动信号的方法利用随机声源(例如船舶噪声)来对信道响应进行估计，由于无法预知声源频谱，仅从阵列接收到的信号中对信道响应和声源频谱进行估计，会遇到难解的盲解卷积问题。然而，如果已知关于信道响应结构的部分先验信息(例如，由于海洋信道多途效应使声场呈现射线到达结构)，则盲解卷积问题变得可解[2]。最近的研究已经证明了基于射线的盲解卷积方法(Ray-based blind deconvolution,RBD)估计信道响应的可靠性。当声源为可控通信声源或船舶噪声时，RBD 方法可以只利用接收阵阵型信息和阵列位置处的声速剖面(Sound speed profile,SSP)信息来估计信道响应。

已有的研究已验证了RBD 方法在水平面海底的海洋波导环境中估计到的信道响应(以下简称为RBD-CIR)的准确性。例如，在相位方面，利用RBD-CIR 的到达时间信息，可进行声源定位[3−5]、接收阵阵型检测[6−7]以及被动声层析[6]等。在幅度方面，张雪冬等[8−9]通过RBD-CIR 的直达波与海底反射波幅度之比并对偶极子效应修正得到了海底反射损失，反演了海底参数，验证了RBD-CIR幅度信息的准确性。以上研究均基于海洋波导为水平面海底的情况，本文对于斜坡海底(海深随距离变化)环境下，RBD 方法估计得到的信道响应的准确性和有效性进行验证和讨论。主要内容分为以下几个部分：首先介绍了基于射线的盲解卷积方法的基本原理；然后利用仿真数据，验证了水平面海底时RBD 方法的有效性；接着仿真比较了海底坡度不同时RBD 方法所得信道响应，并对海底坡度和信噪比(Signal-to-noise ratio,SNR)对RBD-CIR的影响进行了讨论；另外还对具有一定粗糙度的海底斜坡波导中或存在海底山丘的波导中，RBD 方法的有效性进行了讨论；最后对本文进行了总结。

1 RBD方法[2]

利用基于射线的盲解卷积方法估计CIR。假设未知源发出的角频率为ω的信号可表示为

其中，Φs(ω)为声源相位谱。那么第j个接收水听器的接收信号频谱为

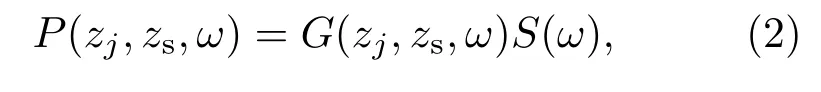
其中，G是频域信道响应函数，zs是声源深度，zj是由N个阵元组成的接收阵中第j(j= 1,2,···,N)个水听器的深度。当海洋信道多途效应使声场呈现射线到达结构时，该信道响应可以表示为多条射线路径的叠加[10]，

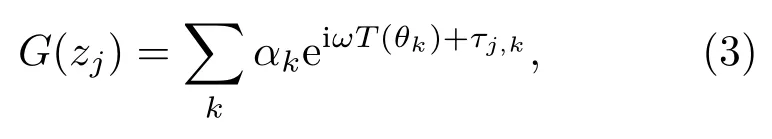
其中，αk表示第k条射线路径的幅度；T(θk)为从声源到接收阵的第k条射线路径的传播时间，θk为第k条射线的到达角；τj,k表示第k条射线路径到达第j个阵元与到达参考阵元的时间差。因此，与特定到达角θk相关联的特定入射波可以在接收端通过宽带波束形成(例如常规波束形成[11])被分离出来。假设该阵列具有足够的空间分辨率，使得其他射线路径上的能量旁瓣最小，则有

其中，B(ω;θk)为接收信号在第k条射线到达角θk方向上的波束形成结果。令

利用公式(5)，可得归一化信道响应

在浅海中，通常假设公式(6)中的分母在频率上足够恒定，通过平方根项的归一化消除了声源信号幅度的影响。此外，通过将估计的信道响应Ge(zj,zs,ω;θk)与接收数据P(zj,zs,ω)(j= 1,···,N)做解卷积可以估计原始声源的波形，即声源波形可以表示为

其中，∗表示取共轭。

2 水平面海底信道

首先验证水平面海底信道时RBD 方法的有效性。利用射线模型对2016年美国圣巴巴拉海峡实验进行仿真，仿真环境如图1(a)所示。假设海底斜坡坡度ϕ=0◦，即信道为深600 m的水平不变波导。声源位于海面以下10 m 处，发射带宽150∼500 Hz的白噪声信号。31 元的垂直接收阵(Vertical line array,VLA)深度为510∼540 m，阵元间隔为1 m。以接收阵处为0 点，水面舰船从距接收阵1.0 km处逐渐航行至3.5 km 处。声速剖面由16 个温盐深仪(Conductivity,temperature,depth,CTD)所测数据的平均值所得，如图1(a)中蓝线所示。海底为半无限空间，海底声速cb、密度ρb和吸收系数αb分别设为1600 m/s、1.6 g/cm3和0.5 dB/λ。利用Bellhop[12]对声场进行仿真。当声源-接收阵距离r为2.5 km 时，其CIR 如图1(b)所示，此时可以看出明显的3 条射线路径：直达波、海底反射波以及海底-海面反射波。

图1 仿真环境示意图及利用Bellhop 产生的CIR 图Fig.1 The environment model and the CIR synthesized by Bellhop

以声源-接收距离r=2.5 km为例，图2介绍了利用RBD 方法估计信道响应的详细的步骤。将声源发出的白噪声信号与CIR 理论值在频域做乘法(公式(2))，得到接收信号。图2(a)为VLA 上第一个阵元(510 m)处的接收信号。对VLA所有阵元的接收信号做常规波束形成所得波束图如图2(b)所示，其中红点表示的直达波到达角和海底反射波到达角分别为θ1=−13◦和θ2= 16◦(其坐标定义见图2(e))。对VLA 所有阵元的接收信号在直达波到达方向θ1上做波束形成(公式(4))，将波束形成后的信号与接收信号做匹配滤波，然后对幅度进行归一化(公式(5)∼(6))，得到RBD-CIR如图2(c)所示。其对应的VLA 接收深度上的CIR 理论值如图2(d)所示。为了便于比较，将RBD-CIR 的直达波在第一个VLA 阵元上的到达时间人工平移到1 s 处。可以看出，CIR 与RBD-CIR 在幅度和相位上均符合得很好。由于RBD方法通过对接收信号做波束形成(公式(4)) 来估计随机声源的相位，因此无法估计出声源与接收阵之间的绝对到达时间，所以图2(c)与图2(d)时间轴是不同的。

对声源-接收阵之间不同距离上的接收信号进行空间滤波，对应的波束形成结果见图3(a)，并利用Bellhop 计算直达波到达角θ1和海底反射波到达角θ2的理论值，用+表示(图3(a))。利用不同声源-接收距离上的直达波到达角θ1的波束形成结果得到RBD-CIR，并将RBD-CIR 与其对应的CIR理论值做相关，并将互相关系数在深度上做平均，得到平均互相关系数，

图2 利用RBD 方法估计信道响应的实现步骤及到达角坐标系定义Fig.2 The steps for estimating CIR using RBD method and the coordinate for arrival angle

其中，xcorr 表示求互相关系数。所得的平均互相关系数随距离的变化关系如图3(b)中蓝线所示。图3(b)中其他曲线为对接收信号增加不同SNR 的噪声时，其平均互相关系数随距离的变化关系。可以看出，随着SNR 的减小，平均互相关系数也在随之减小。一般认为，归一化相关系数大于0.7时，两点间的声场相关性较好，所以这里两信道响应间相关性的判别也选取了0.7 作为参考依据，李整林等[13]也有类似处理。当SNR小于10 dB时，平均互相关系数小于0.7，表明RBD-CIR与CIR的相关性非常小或不相关，RBD 对CIR 的估计无效。当SNR 不同时，随着声源-接收距离r的增加，平均互相关系数均逐渐增大，这意味着估计到的RBD-CIR 越准确。这是由于随着声源-接收距离r的增加，声源所发出的信号在接收阵上越接近平面波，波束形成的结果越精确，从而估计的RBD-CIR越精确。

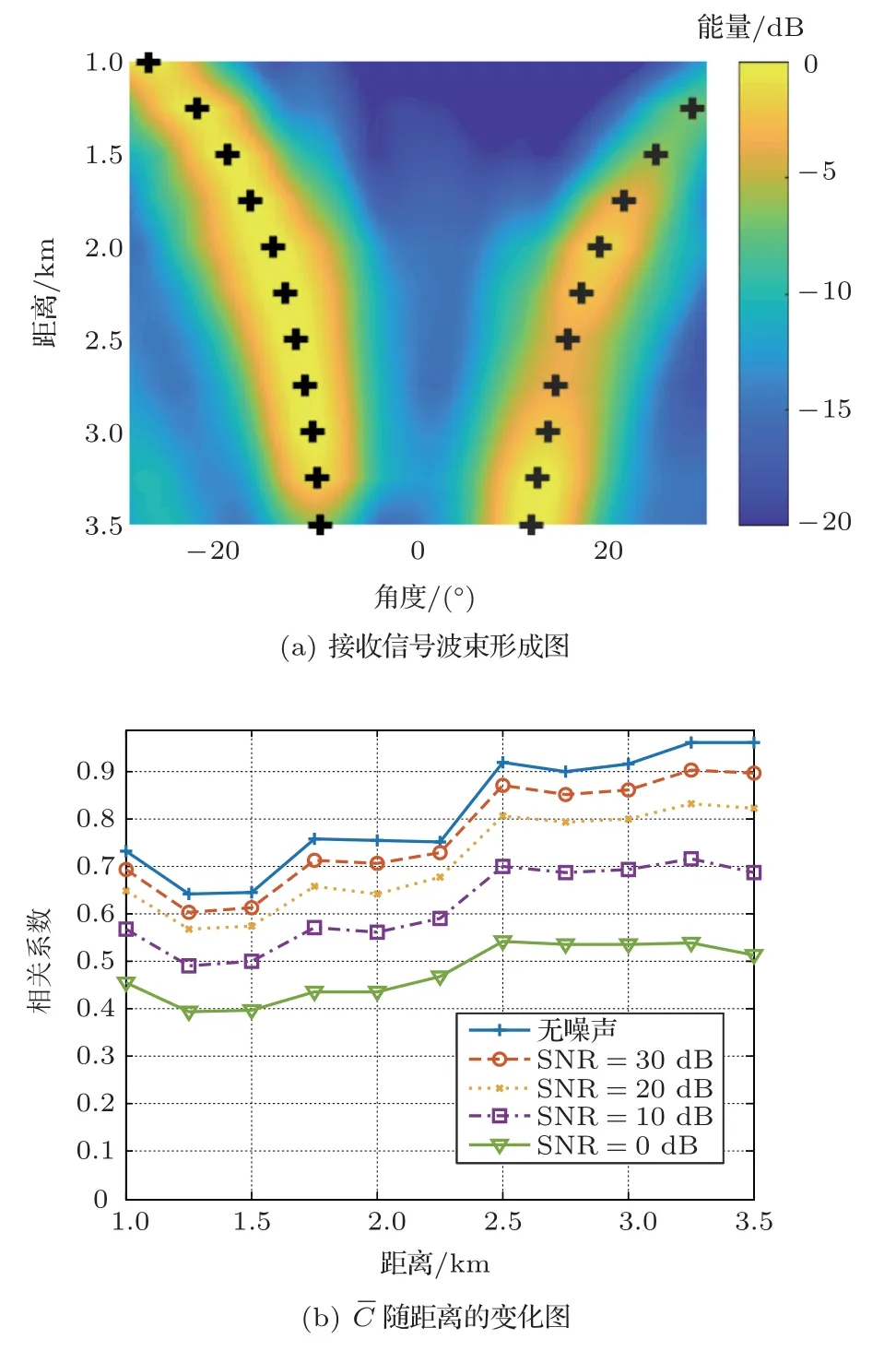
图3 ϕ=0◦时波束形成结果及随距离的变化图Fig.3 Evolution of the beamforming patterns andalong increasing source-receiver distances when ϕ=0◦

3 平斜坡海底信道

RBD 方法在水平海底时对CIR 的估计效果已被很多研究验证[1−9]，但在斜坡海底时的研究还很欠缺。这一部分介绍了当海洋环境的海底坡度ϕ不等于0◦时(如图1(a)所示)，RBD 方法对CIR 的估计效果。图4(a)为声源-接收距离r为2.5 km，海底坡度ϕ分别为−2◦、0◦、1◦和5◦时，对接收信号做常规宽带波束形成的结果。受VLA 深度的限制，这里仅对>−2◦的平海底斜坡进行了讨论。如图4(a)所示，直达波的到达角θ1=−13◦不随海底坡度ϕ变化；但海底反射波的到达角θ2随海底坡度的增加而增大，且由于海底反射损失的影响，其在θ2处的幅度随着坡度的增加ϕ而减小。对于半无限空间的海底，其海底反射损失(Reflection loss,RL)[10]可表示为

其中，cw、ρw、θw和θb分别表示在接近海底处海水的声速、密度，声线入射角和透射角。透射角和入射角的关系根据Snell定律[10]得到

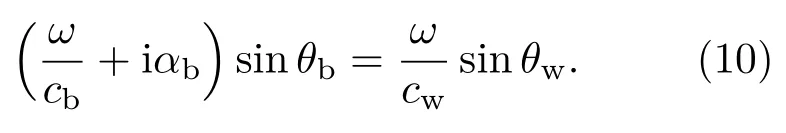
由于αb与ω成正比，所以RL与ω无关。根据图1(a)海底参数所得到的海底反射损失与声线入射角θw的关系如图4(b)所示。当海底坡度ϕ越大时，其入射角θw越小，海底反射损失RL 越大，导致海底反射波的幅度越小。

图4 不同海底坡度ϕ 下的波束图及海底反射损失随入射角的变化图Fig.4 Beamforming pattern for different slope angle ϕ and the relationship between RL and the incident angle

对比海底坡度ϕ分别为−2◦、1◦和5◦时的CIR(图5 第 一 列)与RBD-CIR(图5 第 二 列)在 声源-接收间距r为2.5 km 处的结果可以看出，当海底坡度不同时，RBD均可以对CIR的幅度和相位进行较为准确的估计。在这里，与水平面海底的情况类似，也将RBD-CIR 的直达波在第一个VLA 阵元上的到达时间人工平移到1 s处。由于RBD 方法无法估计出声源与接收阵之间的绝对到达时间，所以图5的第一列与第二列的时间轴是不同的。

当海底坡度ϕ分别为−2◦、1◦和5◦时，对所有不同声源-接收距离r的信号做波束形成(见图6)，并利用Bellhop 计算直达波到达角θ1和海底反射波到达角θ2，用+表示(见图6)。利用不同声源-接收距离r上的直达波到达角θ1的波束形成结果估计其对应的RBD-CIR。当SNR和海底坡度ϕ不同时，其RBD-CIR 与CIR理论值的平均互相关系数随距离的变化关系如图7所示。可以看出，对于所有的海底坡度情况，均随着声源-接收距离r的增加而增加，并随着SNR的减小而减小。当SNR<10 dB时，平均互相关系数0.7，表明RBD-CIR 与CIR的相关性非常小或不相关，RBD对CIR的估计无效。

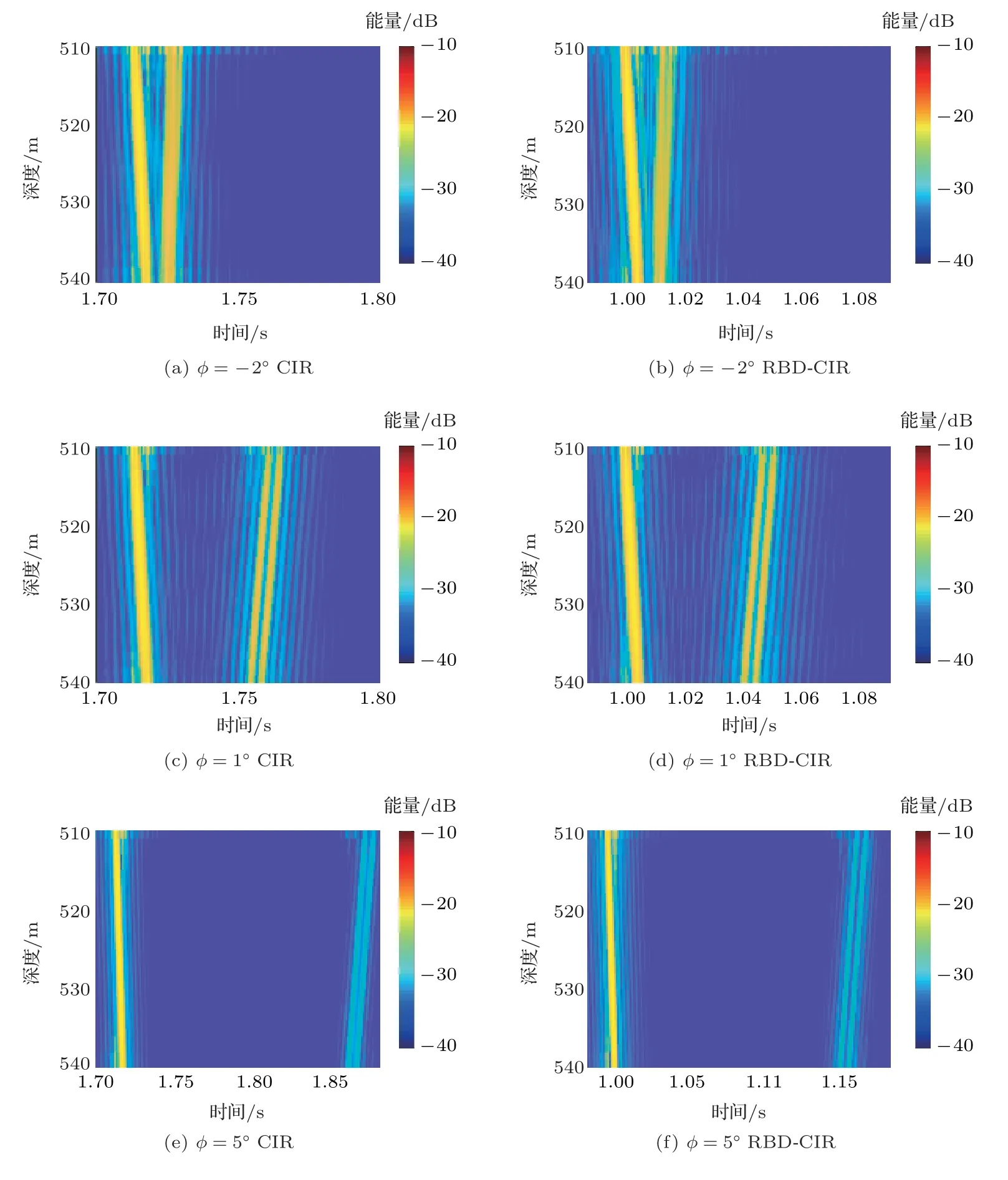
图5 当r =2.5 km 时，CIR 理论值及其对应的RBD-CIR 在不同海底坡度ϕ 下的结果Fig.5 The CIRs and their corresponding RBD-CIRs for different slope angle ϕ at the source-receiver distance r of 2.5 km

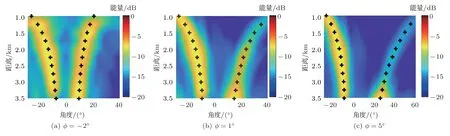
图6 海底坡度ϕ 不同时，波束形成结果及由Bellhop 得到的到达角理论值(黑色加号)随距离的变化关系Fig.6 Evolution of the beamforming patterns along increasing source-receiver distances and their corresponding arrival angle calculated by Bellhop (dark plus signs) with different slope angle ϕ

图7 海底坡度ϕ 不同时，CIR 与RBD-CIR 的平均互相关系数随距离的变化关系Fig.7 Evolution of mean correlation coefficients along increasing source-receiver distances with different SNR for different slope angle ϕ

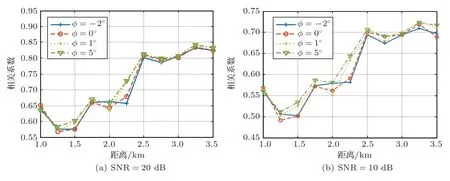
图8 海底坡度ϕ 不同时，CIR 与RBD-CIR 平均互相关系数随距离的变化关系Fig.8 Evolution of mean correlation coefficients along increasing source-receiver distances for different slope angle ϕ

为了比较同一SNR时，不同海底坡度ϕ对平均互相关系数的影响，以SNR 为20 dB 和10 dB，海底坡度ϕ分别为−2◦、0◦、1◦和5◦为例，其随声源-接收距离r的变化关系如图8 所示。可以看出，对于不同的SNR，随着ϕ的增加而略微增大，尤其在r=2.25 km 处，最大增值可以达到0.07。这是由于当海底坡度较大时，海底反射损失越大，其他路径(例如海底反射波)的接收信号对直达波路径的接收信号干扰越小，从而使得估计的RBD-CIR 越准确，越大。

4 粗糙斜坡信道

当海底坡度ϕ为1◦时，为了对粗糙平海底斜坡情况进行仿真，令海底在每距声源的水平距离为50 m 处发生一次随机起伏，该起伏服从均值为0 m、方差分别为0.5 m 和2.5 m 的正态分布，所得海底斜坡地形分别如图9(a)和图9(d)所示，来模拟相对平滑和相对粗糙的海底情况，其他环境参数与图1(a)中相同。利用Bellhop 得到的信道响应理论值分别如图9(b)和图9(e)所示。海底相对平滑时，海底反射波较为清晰；海底相对粗糙时，海底反射波受到较大影响，能量降低。利用RBD 方法对随机声源(在这里选取为白噪声)在150∼500 Hz产生的接收信号进行处理，所得RBD-CIR 分别如图9(c)和图9(f) 所示。利用公式(8)得到CIR 理论值与相应RBD-CIR 的平均互相关系数分别为0.93 和0.94，可以看出不同海底粗糙度情况下，RBD-CIR与CIR均符合得很好。由于该RBD 方法在对接收信号进行波束形成时，利用直达波的到达角来得到声源的相位，所以不受海底情况的影响，RBD 方法依然是有效的。

图9 海底斜坡较光滑(第一行)和较粗糙(第二行)情况下的海底地形图、CIR 理论值和RBD-CIR 结果Fig.9 The bottom geometry,the CIRs,and their corresponding RBD-CIRs for smooth (upper panel) and rough (lower panel) bottoms,respectively

5 信道中存在山丘的情况

对海底存在较小幅度的山丘的情况进行讨论，海底分布如图10(a)所示。在离VLA 水平距离0.15∼0.40 km 处存在一个海底山丘，其高度随距离的变化服从正弦函数的半周期，幅值为110 m。当声源-接收距离为2.5 km、接收深度分别为510 m和551 m 时，由Bellhop 所得的直达波如图10(a)所示。由图10(a)可以看出，当接收深度为551 m 时，直达波声线与山丘相切，当接收深度大于551 m 时直达波无法抵达接收阵元处，即在此距离上直达波最深可抵达深551 m 的接收阵元。图10(b)为31阵元的VLA 深度分别为510∼540 m、540∼570 m以及570∼600 m，声源-接收距离为2.5 km 时，对接收信号做常规宽带波束形成的波束图结果。当VLA深度为510∼540 m时，波束图在直达波方向上(−13◦)的能量最高；当VLA 深度为540∼570 m 时，波束图在直达波(−13◦)和海底-海面反射波(−36◦)方向上具有相当的能量；当VLA深度为570∼600 m时，波束图在海底-海面反射波方向上(−36◦)的能量最高。

图11 为VLA 深度分别为510∼540 m 和540∼570 m 时，在声源-接收距离为2.5 km 处的CIR 理论值(第一列)和其对应的RBD-CIR(第二列)，这里RBD 方法所使用的波束形成角度为直达波到达角(−13◦)，两种情况所得RBD-CIR 与其理论值的平均互相关系数分别为0.93和0.71，估计结果有效。

图10 海底山丘地形图及VLA 深度不同时的波束图Fig.10 The bottom geometry with a hill and the beamforming pattern for different VLA depth

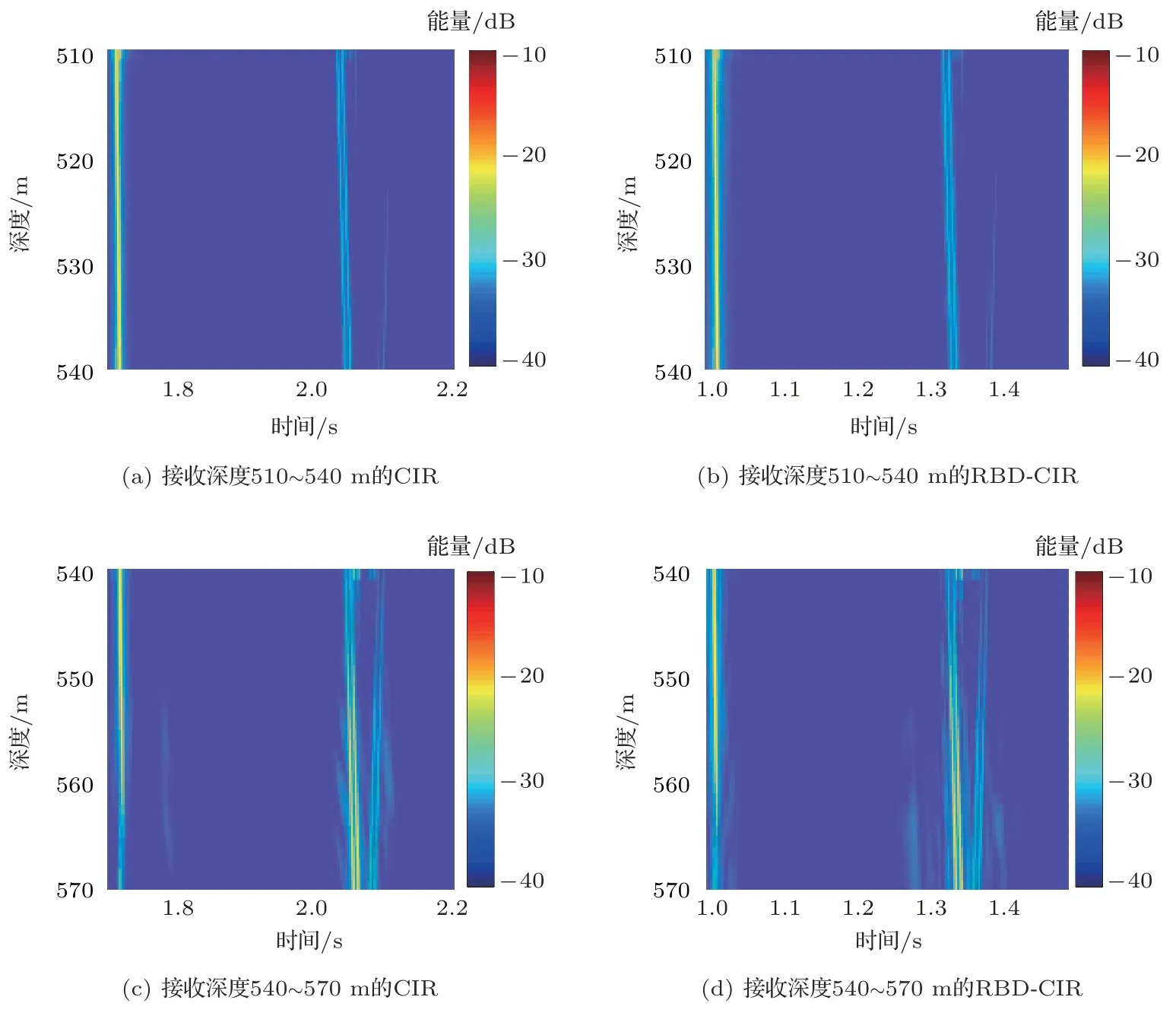
图11 当VLA 深度不同时，在声源-接收距离r = 2.5 km 处的CIR 理论值(第一列)及其对应的RBD-CIR(第二列)结果，其中波束形成角度(θ =−13◦)为直达波到达角Fig.11 The CIRs (first column) and their corresponding RBD-CIRs (second column) for different VLA depth with the source-receiver distance r of 2.5 km,where the beamforming angle (θ =−13◦) is the direct arrival angle

图12 当VLA 深度不同时，在声源-接收距离r =2.5 km 处的CIR 理论值(第一列)及其对应的RBD-CIR(第二列)结果，其中波束形成角度(θ =−36◦)为海底-海面反射波到达角Fig.12 The CIRs (first column) and their corresponding RBD-CIRs (second column) for different VLA depth with the source-receiver distance r of 2.5 km,where the beamforming angle (θ = −36◦) is the bottom-surface arrival angle

6 结论

本文对2016年美国圣巴巴拉海峡实验进行仿真，验证了水平面海底和斜坡海底时，利用RBD 方法来估计信道CIR 的有效性，并讨论了不同信噪比和坡度下，RBD-CIR 与CIR 理论值之间的平均互相关系数随声源-接收距离的变化关系。可以看出，对于不同坡度的平斜坡海底信道，RBD方法估计到的CIR 在幅度与相位上均与实际CIR 符合得较好。对于同一坡度的海底，平均互相关系数随着信噪比和声源-接收距离的增大而增大。当信噪比大于10 dB 时，RBD 方法可以对CIR 进行有效估计。当信噪比固定时，海底坡度的增加会使得海底反射损失增大，令其他路径的信号对直达波路径信号的干扰减小，从而导致平均互相关系数增大。在斜坡信道比较粗糙或信道中存在海底山丘的情况下，RBD方法仍可对CIR进行有效的估计。由于本文主要基于仿真数据，对于实际应用时RBD 方法在斜坡海底波导中的有效性仍需进一步验证与讨论。图12 为VLA 深 度 分 别 为540∼570 m 和570∼600 m 时，在声源-接收距离为2.5 km 处的CIR 理论值(第一列)和其对应的RBD-CIR(第二列)，这里RBD方法所使用的波束形成角度为海底-海面反射波到达角(−36◦)，两种情况所得RBD-CIR 与其理论值的平均互相关系数分别为0.71 和0.84，估计结果依然有效。因此当海底山丘对直达波有遮挡作用时，RBD方法可以利用其他射线路径的到达角度对接收信号做波束形成，以估计随机声源的相位，进而对CIR进行有效估计。