随钻声波测井隔声体刻槽影响的数值模拟研究∗
杨培年 陈德华 潘 钥 张 咪
(1 中国科学院声学研究所 声场声信息国家重点实验室 北京 100190)
(2 中国科学院大学 北京 100049)
(3 北京市海洋深部钻探研究中心 北京 100190)
0 引言
随钻测井技术可用于常规电缆测井无法适用的大斜度井、水平井等复杂井况,而且“边钻边测”的工作模式可大幅节省海洋油气资源探测过程中钻井平台占用所产生的高额成本,加之随钻测井技术可实时测量未受泥浆污染的原始地层的信息,因而在近年来得到了快速发展,并已在国内外得到广泛的应用;随钻声波测井得到的地层参数信息可以用来预测地层压力、判断井壁稳定性以及估计地层孔隙压力等;在油气探测和评价过程中,随钻测井技术相比于随钻中子和密度测井,测量孔隙度时更安全环保,是近年来国内的一个研究热点。与电缆测井相比,随钻声波测井中会有直接沿着钻铤传播的钻铤波,钻铤波会严重干扰接收到的地层波信息,因此,隔声体的设计是随钻声波测井的关键技术之一[1]。它用于阻隔钻头在钻井过程中所产生的噪声以及发射换能器工作时在钻铤中所产生的钻铤波。
国内外学者对随钻声波测井中的钻铤波传播特性以及隔声体设计进行了很多研究工作。Tang等[2]提出钻铤波在频率域中存在一个固有阻带,频谱阻带的位置与钻铤的尺寸相关,但是这个固有阻带的带宽比较小,难以满足测量地层波的需求。Aron等[3]提出在声源发射器和接收器之间的钻铤上进行刻槽来衰减直接在钻铤上传播的钻铤波,可以拓宽隔声体的频率域的阻带。杨勇等[4]利用三维有限差分法对随钻声波测井隔声体的隔声效果进行数值模拟,结果发现周期性交错排列的凹槽结构的隔声体在测量地层纵波速度时具有较好的效果。闫向宏等[5]利用二维有限元方法数值模拟研究了周期性轴对称凹槽的尺寸和结构对隔声效果的影响。刘彬等[6]对周期性非对称空槽结构隔声性能进行数值模拟,给出了隔声效果与空槽结构尺寸的关系。Su 等[7]提出了一种在钻铤上变径隔声技术。Zheng 等[8]通过计算声场函数极点和支点的贡献单独分析了钻铤波和纵波的激发强度,并指出在地层的影响下钻铤波固有阻带将会消失。Wang 等[9]分析了钻铤波的参数对钻铤波的影响并提出波阻抗大的材质制作的钻铤有利于实现钻铤波和地层纵波的分离。Yang 等[10]利用有限差分模拟了不同钻铤的随钻声场并通过对比表明钻铤波的一些传播特性:(1) 内刻槽在一定频率范围内好于外刻槽;(2) 干扰波不仅有直达的钻铤波,还有反射的钻铤波和转化的斯通利波等。Wang 等[11]创造性地提出了广义钻铤波理论,该理论认为接收器接收到的钻铤波包括两部分:一部分是直接沿着钻铤传播到达的直接钻铤波,另一部分是由于井孔的作用而产生的间接钻铤波。He 等[12]通过波场分离计算了两种钻铤波的波形,揭示了两种钻铤波的传播机制。Ji等[13]研究不同频率段钻铤波在径向的激发幅度,表明高频(17 kHz 以上)时外刻槽要好于内刻槽,但是并没有考虑均匀凹槽深度对结果的影响。
虽然很多学者通过理论和数值模拟结果揭示了钻铤波的传播规律[14],但是仍然还有部分问题尚未解决或者还有部分争议的地方。He 等[12]和Ji等[13]的研究工作表明钻铤波径向位置激发幅度峰值偏向内径,则说明内刻槽要好于外刻槽,实际上考虑的只是凹槽深度为2 cm 的情形。刻槽隔声体虽然可以衰减钻铤波,同时也会产生幅度较大的散射波,这些波同样会干扰后续的地层横波、伪瑞利波以及斯通利波。所以也有必要研究散射波是怎么形成的,以及不同隔声体刻槽的影响。
本文利用二维有限元数值模拟方法首先研究了单个凹槽隔声体在无限大流体中的散射波,分析了凹槽界面散射波的类型。然后研究了不同频率下均匀内外刻槽衰减钻铤波的效果,同时考虑槽深的变化对均匀内外刻槽效果的影响。最后研究了不同刻槽结构对散射波的影响,对比分析了均匀凹槽和渐变凹槽后散射波对后续波的影响。
1 井孔模型和参数
随钻声波测井模型可以简化为如图1所示的柱状径向分层结构。整个径向分层结构从内到外分别是钻铤内部的内环流体、钻铤、钻铤外部的外环流体以及地层,介质参数和尺寸如表1所示。本文以文献[15]使用的二维柱坐标时域有限差分法(Finitedifference time-domain,FDTD)研究地层各向异性的算法为基础,研究随钻情况下的井孔声场。由置于钻铤外表面的单极子声源激发轴对称波场,声源波形为余弦包络脉冲,具体表达式见文献[16]。本文有限差分计算模型的参数如下:径向R方向最大为0.75 m,轴向Z方向最大为5.1 m。隔声体尺寸如表1 所示。R方向和Z方向的采样空间间隔均为0.002 m。声源与接收器的径向位置为0.09 m,接收器阵列的轴向位置无特殊说明为3.0∼4.0 m,相邻接收器间距为0.05 m,采样时间长度为4 ms。需要说明的是,本文假设井内流体为理想流体,地层为各向同性均匀弹性固体。由于模拟过程中地层没有设置Q值衰减,实际随钻声波测井的钻铤波对地层波的干扰更加显著。
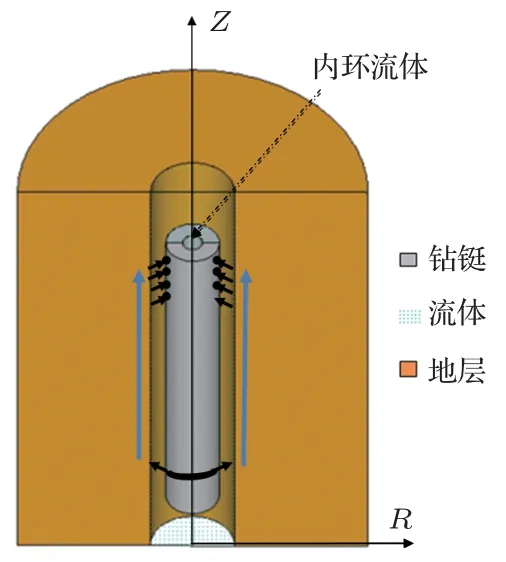
图1 随钻声波测井示意图Fig.1 The diagram of acoustic logging while drilling

表1 随钻声波测井的介质参数和尺寸Table 1 Medium parameters and dimensions of acoustic logging while drilling
2 钻铤在无限大流体中的数值模拟
隔声体刻槽以后,钻铤波会在刻槽界面进行来回的反射。Yang 等[10]通过计算假想截断钻铤模型的波场,分析表明钻铤波在刻槽界面透射的斯通利波同样会掩盖地层纵波。但是截断后的钻铤与刻槽的钻铤并不一样,钻铤刻槽后钻铤波的散射更加符合实际隔声体的情况。因为钻铤在有地层时,除了钻铤波以外还有地层波、伪瑞利波和斯通利波,此时钻铤波的散射波会与地层波混叠,不容易分析其类型。为了便于分析钻铤波的传播特征以及在刻槽界面的散射特性,本文假想了如图2(a)所示的只刻一个较深凹槽的钻铤隔声体结构,并且假想钻铤在无限大流体中,然后计算整个波场。为了方便显示散射波波形,接收器阵列源距选取为4∼5 m。
图2(a)为只刻一个小槽的隔声体模型,槽宽为0.1 m,槽深5 cm,刻槽起始位置在与声源相距1.5 m。声源中心频率为8 kHz,脉冲宽度为0.5 ms。图2(b)为钻铤在无限大流体中刻单个凹槽隔声体后5 m 源距处全波波形。图2(c)为不刻槽时5 m源距处全波波形,由于没有地层,在无限大流体模型中,光滑钻铤模型中的全波波形只有钻铤波和斯通利波。很明显,在图2(b)中钻铤波和斯通利波之间还有一个由刻槽后引起的散射波波形。图3(a)为不同源距波形叠加在一起,相邻波形源距为0.05 m。容易看出,“多余”的波包本身包含多模式频散,其主要部分和斯通利波的速度很接近。然后通过时间相关叠加,得到上述波形的时间慢度图,如图3(b)所示。从慢度图中也可以看出,该波的慢度基本与斯通利波的慢度一致。经以上分析可知,该波主要是钻铤波在刻槽界面散射形成的斯通利波。

图2 钻铤在无限大流体中单个凹槽隔声体模型及5 m 源距全波波形Fig.2 Acoustic insulation model with a single groove in infinite fluid and full waveform at source distance of 5 m

图3 钻铤在无限大流体中单个凹槽隔声体后数值模拟Fig.3 Numerical simulation of drill collars with a single groove acoustic isolator in an infinite fluid
3 钻铤在井孔地层中的数值模拟
为了突出刻槽对钻铤波的散射特征,上述算例中只考虑钻铤放在无限大流体中,但是实际上地层也会影响钻铤波的幅度[12],所以下面考虑钻铤在地层井孔中的情况。文献[10,12]表明内刻槽在特定频率范围内好于外刻槽,这个结论实际上只是考虑了凹槽深度在2 cm 的情况。本文研究凹槽深度变化时内外刻槽在一定频段内的隔声性能好坏。
图4 为钻铤放置于无限大地层中的均匀内外刻槽的计算模型。图4(a)为均匀内刻槽模型;图4(b)为均匀外刻槽模型,凹槽宽度和凹槽间隔均为0.1 m,凹槽个数同为10。图5(a)给出中心频率8 kHz 时钻铤波波能量在钻铤中的分布,波场快照中的能量用波场计算结果中的径向应力来表征。图5(b)为图5(a)中红框区域的能量分布放大图。此时声源主频为8 kHz,频率范围主要在4 kHz∼12 kHz。钻铤波能量的传播速度主要取决于群速度,而钻铤波在4 kHz∼12 kHz 范围内的群速度是高度频散的,不同频率部分钻铤波的能量传播速度也就不同,而能量幅度主要取决于该频率成分在频谱中的幅度。由于接收波形的频谱幅度在11 kHz附近达到最大,而钻铤波在11 kHz时的群速度约为3500 m/s,所以在1 ms 时刻时的波场快照中,钻铤波在钻铤3.5 m处附近有最大能量。钻铤内径为0.027 m,钻铤外径为0.09 m。由图5(b)可以明显看到,钻铤波能量分布的峰值确实是偏向于钻铤内径。
本文首先计算了凹槽深度为2 cm 时内外刻槽后钻铤外表面4 m 源距处接收波形。为了便于比较内外刻槽对钻铤波的衰减,图5 中只考虑前1.6 ms波形。图6(a)为声源中心频率7 kHz∼10 kHz 时内外刻槽后的前1.6 ms 接收波形,图6(b)为声源中心频率11 kHz∼14 kHz时的接收波形。图中c代表钻铤波,p 代表地层纵波。图中可以看到,内刻槽后的钻铤波波形幅度在7 kHz∼10 kHz范围内要略小于外刻槽,在10 kHz 以上频率范围内明显要小于外刻槽。为了更加直观地比较内外刻槽在不同频率下隔声性能,分别计算内外刻槽在凹槽深度为2 cm时的频谱曲线,如图6(c)所示。频谱曲线的计算方法可参考隔声量计算的方法。图6(c) 显示,内刻槽的频谱幅度在7 kHz∼10 kHz频率范围内与外刻槽相当,在10 kHz∼15 kHz 范围内明显低于外刻槽,这与波形幅度的结果是一致的。所以在凹槽深度为2 cm 的内刻槽在本文考虑的频率范围内隔声效果是要好于外刻槽的。该结果与之前的结论是一致的。

图4 井孔地层中均匀内刻槽和外刻槽的隔声体计算模型Fig.4 Acoustic isolator calculation model of uniform internal and external grooves in borehole formation
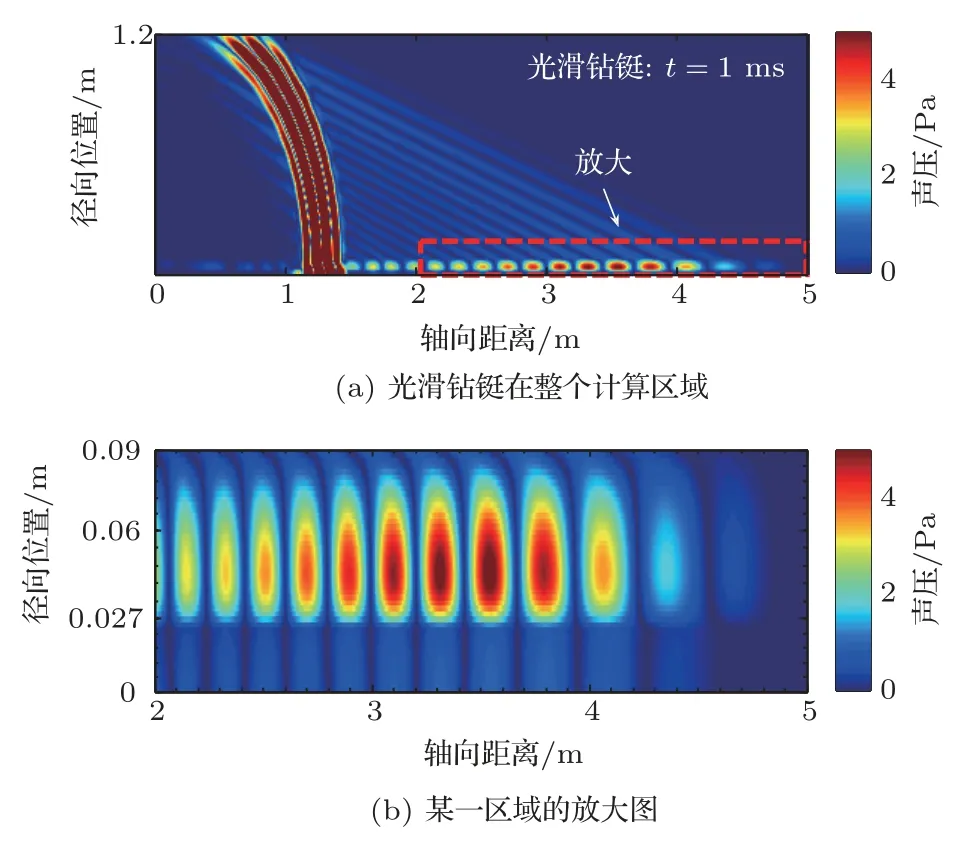
图5 波场快照图Fig.5 Snapshot of wave field
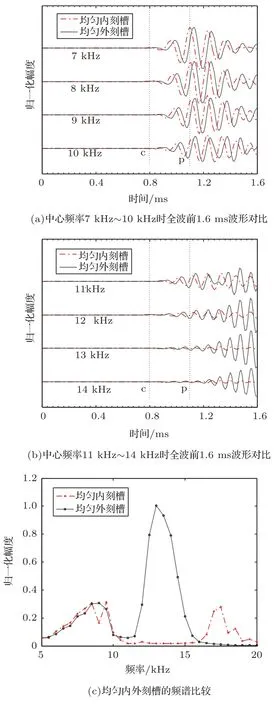
图6 硬地层中FDTD 模拟的均匀内刻槽与外刻槽槽深2 cm 时波形和频谱对比Fig.6 Waveform and spectrum comparison of uniform internal grooves simulated by FDTD with external grooves 2 cm deep in hard formation
本文还计算了凹槽深度为2.5 cm 时内外刻槽后钻铤外表面4 m源距处接收波形。图7(a)为声源中心频率7 kHz∼10 kHz时内外刻槽后的前1.6 ms接收波形,图7(b)为声源中心频率11 kHz∼14 kHz时的接收波形,图7(c)为内外刻槽在凹槽深度为2.5 cm 时的频谱曲线。此时在7 kHz∼10 kHz 频率范围内,外刻槽后的钻铤波波形略小于内刻槽。图7(c)的频谱曲线表面,外刻槽在10 kHz 以下的频谱幅度要略小于内刻槽,在11 kHz∼16 kHz频率范围内要大于外刻槽。频谱曲线的结果与波形比较的结果也是一致的。所以在凹槽深度为2.5 cm 时,外刻槽在10 kHz 频率以下时要好于内刻槽的。此结果与凹槽深度为2 cm时是不一样的,说明凹槽变化会影响内外刻槽的隔声性能好坏比较。为进一步研究凹槽深度变化是会怎么影响两者隔声好坏的,下面再考虑凹槽深度为3 cm的情况。
最后计算了凹槽深度为3 cm 时内外刻槽后钻铤外表面4 m源距处接收波形。图8(a)为声源中心频率7 kHz∼10 kHz时内外刻槽后的前1.6 ms接收波形,图8(b)为声源中心频率11 kHz∼14 kHz时的接收波形,图8(c)为内外刻槽在凹槽深度为3 cm时的频谱曲线。此时在7kHz∼11 kHz频率范围内,外刻槽后的钻铤波波形明显小于内刻槽。尤其中心频率为10 kHz时,外刻槽后的钻铤波形相比于内刻槽小很多。图8(c)的频谱曲线显示,外刻槽在10 kHz以下的频谱幅度要小于内刻槽,在11 kHz∼16 kHz频率范围内要大于外刻槽。频谱曲线的结果与波形比较的结果也是一致的。槽深在2.5 cm 以上时,均匀内刻槽和外刻槽对钻铤波衰减的结论确实与钻铤波能量峰值偏向钻铤内径不相符合。原因可能是与外径变化相比,钻铤内径变化使得钻铤波能量峰值在钻铤上的分布更加显著地向右偏移,即钻铤外表面接收到的钻铤波幅度相对较大。
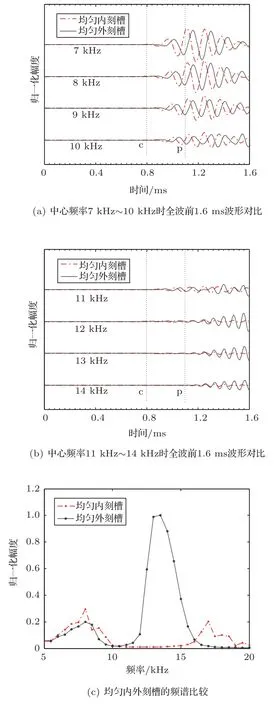
图7 硬地层中FDTD 模拟的均匀内刻槽与外刻槽槽深2.5 cm 时波形和频谱对比Fig.7 Waveform and spectrum comparison of uniform internal grooves simulated by FDTD with external grooves 2.5 cm deep in hard formation

图8 硬地层中FDTD 模拟的均匀内刻槽与外刻槽槽深3 cm 时波形和频谱对比Fig.8 Waveform and spectrum comparison of uniform internal grooves simulated by FDTD with external grooves 3 cm deep in hard formation
通过上面的分析可知,当凹槽深度较小(2 cm)时,在整个7 kHz∼15 kHz 频率范围里外刻槽的效果都不如内刻槽,尤其是在11 kHz 以上,内刻槽相比于外刻槽的隔声性能好很多。当增加槽深到2.5 cm 时,外刻槽在7 kHz∼10 kHz 频率范围内的隔声性能优于内刻槽。对比内刻槽和外刻槽情形下的波形频谱,其结果与波形对比结论是一致的。当进一步增加槽深至3 cm 时,外刻槽在7 kHz∼10 kHz 频率范围内的隔声效果明显好于内刻槽,尤其在10 kHz附近,外刻槽相比于内刻槽的衰减钻铤波幅度更加明显。图9 给出均匀内刻槽和均匀外刻槽在刻槽深度为3 cm时在1 ms时刻的波场快照图,可以明显看到,图9(b)中均匀外刻槽后钻铤波能量明显小于图9(a)中的均匀内刻槽,此结果与前面分析的结论是一致的。所以本文在考虑内外刻槽的隔声效果好坏时,不仅要考虑中心频率的影响,还要考虑凹槽深度的变化的影响。另外,通过对比内刻槽和外刻槽对钻铤波的衰减可以看出,内刻槽可以有效地同时衰减钻铤波高频和低频部分,而外刻槽可以有效衰减钻铤波的低频部分,但对钻铤波高频部分的衰减并不理想。
通过对比图6∼图8,还可发现,槽深逐渐增加,内外刻槽后的波形频谱阻带都逐渐拓宽,钻铤波衰减幅度越来愈大。中心频率较高(11 kHz以上)时钻铤波的衰减随槽深变化更加明显,且外刻槽相对于内刻槽钻铤波波形衰减随槽深变化更明显。

图9 波场快照图Fig.9 Snapshot of wave field
4 刻槽后钻铤波的衰减及散射波
前面考虑了钻铤波导结构对钻铤波传播的影响,但是实际上刻槽后的散射波也会影响后续地层横波和斯通利波的影响。这里着重研究刻槽后的散射波对后续波的影响。
图10(a)为均匀凹槽隔声体,凹槽宽度和间隔都为102 mm,共计12个。图10(b)为前面所述渐变梯度凹槽结构,每段凹槽包括前5 个3 mm 槽宽后6个5 mm槽宽增加的11个小槽,共有6 组。模拟计算中所采用的空间间隔在轴向方向为0.5 mm,径向方向为2 mm。图10(c)为渐变梯度凹槽结构的单个凹槽单元,其中L3= 0.11 m,保持均匀刻槽与渐变刻槽的刻槽长度相同。图11 分别为中心频率13 kHz和15 kHz 时槽宽为0.102 m 和槽宽为0.051 m 的均匀凹槽隔声体的全波波形对比,槽宽较小的均匀刻槽情况下,散射波幅度更小但钻铤波幅度更大。钻铤波在1/4 波长相当的槽宽中传播容易发生谐振,故衰减钻铤波幅度较大,相应的散射波幅度也较大。图12(a)为中心频率是13 kHz时FDTD模拟的渐变梯度凹槽隔声体与均匀凹槽隔声体内刻槽接收器3 m 源距处的全波波形。渐变刻槽后衰减钻铤波的幅度大于均匀刻槽,图12(b)显示渐变刻槽后可以提取得到地层纵波慢度,地层参数见表1 中地层I。图12(b)中还给出了声源放在流体中不刻槽时的全波波形,此时的波形几乎无钻铤波和散射波干扰。可以看到渐变梯度凹槽刻槽后的全波波形中3 ms 处斯通利波之前几乎没有散射波的影响,只有在斯通利波波形后才有散射波的存在。而均匀刻槽后的全波波形中明显会有杂乱波的影响。地层横波波形已经发生明显变化,且在横波与斯通利波之间有幅度非常明显的散射波影响。散射波对地层横波、伪瑞利波以及斯通利波的干扰势必会影响到声波速度信息的提取。均匀刻槽后的散射波比较强,这是因为均匀刻槽的槽宽较大,声波在槽的位置中传播时来回散射形成幅度较大的散射波,而渐变梯度凹槽由于发生局域共振,声波能量主要局限在凹槽里面,所以形成的散射波幅度较小。

图10 均匀凹槽隔声体和渐变凹槽隔声体的二维轴对称模型Fig.10 A two-dimensional axisymmetric model of a uniformly groove insulator and a graded groove isolator

图11 均匀内凹槽与均匀外刻槽4 m 源距处不同中心频率全波波形对比Fig.11 Comparison of the full waveform between the uniform internal groove and the uniform external groove at a source distance of 4 m at the center frequency of 13 kHz and 15 kHz
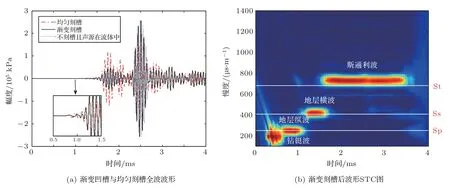
图12 渐变刻槽和均匀刻槽中心频率13 kHz 时3 m 源距处全波波形Fig.12 Full waveform at the center frequency of 13 kHz at a 3 m source distance for the uniform groove and graded groove
5 结论
本文利用有限差分法对随钻声波隔声体相关声场进行了数值模拟,考察了内外刻槽槽深对隔声性能的影响,研究了钻铤波在刻槽界面的散射以及钻铤波能量在钻铤上的分布特征,得到以下主要结论:
(1) 对于钻铤位于无限大流体中且只刻一个凹槽的情况,可以通过波场快照图直观地观察钻铤波、斯通利波及其散射波,刻槽后部分钻铤波会在刻槽界面转化为斯通利波继续向前传播。
(2) 对于钻铤位于井孔地层中的情况,可以发现槽深较小(2 cm)时,内刻槽在7 kHz∼15 kHz整个频率范围衰减钻铤波的幅度都要大于外刻槽;但是当增加槽深至2.5 cm 时,外刻槽在中心频率7 kHz∼10 kHz 范围内的隔声效果要优于内刻槽。也就是说,槽深变化会影响比较内外刻槽隔声性能的结果。当进一步增加槽深至3 cm 时,外刻槽在中心频率7 kHz∼10 kHz范围内衰减钻铤波的幅度明显大于内刻槽。所以当槽深大于2.5 cm 时,外刻槽在10 kHz频率以下的隔声性能要优于内刻槽。
(3) 槽深逐渐增加,内外刻槽后的波形频谱阻带都逐渐拓宽,钻铤波衰减幅度越来愈大。中心频率较高(11 kHz 以上)时钻铤波的衰减随槽深变化更加明显,且外刻槽相对于内刻槽钻铤波波形衰减随槽深变化更明显。
(4) 相比于均匀凹槽,渐变凹槽隔声体刻槽后的散射波幅度较小,对后续的地层横波、伪瑞利波和斯通利波影响较小。
针对以上结论,在工作频率低于10 kHz 时选择均匀外刻槽好于内刻槽。尽量刻更多槽宽较小的渐变凹槽,可以使得刻槽后衰减钻铤波幅度较大,同时也能减小刻槽后散射波的影响。

