谐振式传感器高精度频率测量技术研究*

王 健，杨 挺

（航天长征火箭技术有限公司传感器与系统集成事业部 北京 100076）

引 言

随着MEMS（Micro-Electro-Mechanical System）传感器成本的下降和性能的提升，传统传感器逐渐被淘汰，MEMS 传感器被越来越多的应用于各领域。石英振梁压力传感器、石英振梁加速度传感器、硅谐振压力传感器以及硅振梁加速度传感器等谐振式传感器一般采用自激振荡电路，用频率的变化表征物理量的变化，对频率测量技术提出了更高的要求。例如，压力传感器在某些应用领域需要在20ms的响应时间内达到1ppm 的相对频率精度；加速度传感器在某些应用领域需要在5ms 的响应时间达到1ppm 的相对频率精度。现有的基于单片机的测频方案，利用单片机内部的定时器，基准频率最高只能到60MHz，频率测量精度不能满足要求。因此，有必要研制一种高精度、快响应的频率测量技术。本文提出一种基于FPGA 的测频方案，它具有测量精度高、易于多路扩展、算法易于移植等优点，可满足谐振式传感器的应用需求。

1 硬件架构

硬件系统由晶振、FPGA（Field Programmable Gate Array）和电源模块组成，其中，晶振选用高精度温补晶振（全温区频率稳定性1ppm），FPGA 选用Altera 的Cyclone 系列（内部PPL 模块可以倍频到400MHz），如图1 所示。

由于基于FPGA 的测频算法需要通过边沿检测的时序逻辑电路实现，因此，要将被测信号转换为方波信号。另外，被测信号电平要满足FPGA 的接口电平，该硬件系统利用转换芯片将被测信号转换为3.3V 的方波信号。

基准时钟越高，频率测量精度越高，但需要满足的时序约束也越严格，应该根据需要的频率测量精度选择合适的基准频率。该测频方案利用FPGA 的片上PLL 将外部20MHz 时钟倍频到340MHz，作为测频的基准频率。

由于FPGA 中的乘除法运算需消耗较多资源，因此，该方案利用UART 模块将被测信号周期数和基准信号周期数发给上位机，结合基准信号频率就可以计算出被测信号频率。

测频模块是该频率测量系统的核心。系统采用的基本方法是等精度测频算法，即在采样时间内，同时对被测信号和基准信号进行计数，再计算出被测信号频率。等精度测频算法的相对频率精度只与采样时间和基准频率有关，与被测信号频率无关。

图1 硬件系统框图Fig.1 Hardware system block diagram

2 测频算法

2.1 单边沿检测测频算法

单边沿检测测频算法即为传统的等精度频率测量，是在采样时间内，同时对被测信号fx和基准频率f0进行计数，得到周期数Nx和N0，则由式（1）可以计算出被测频率fx[1]。

假设被测频率计数周期数Nx和基准频率f0恒定，则等精度频率法的相对频率测量精度为

式中，R为相对频率测量精度，Ts为采样周期。

2.2 双边沿检测测频算法

双边沿检测测频算法同时以被测频率的上升沿和下降沿作为实际闸门的开启时间，对基准频率进行计数，如图2 所示。

由式（3）可以计算出被测频率fx。

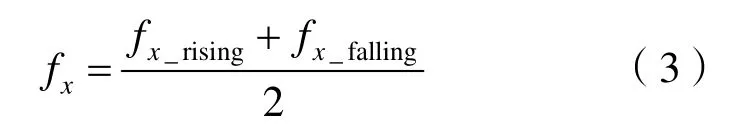
图2 双边沿检测时序图Fig.2 Sequence diagram of double edges detection

式中，fx_rising为上升沿检测的被测频率，fx_falling为下降沿检测的被测频率。

当基准频率信号不是被测频率的整数倍时，由于被测信号和基准信号的相位关系，对基准频率的计数有时会向上取整，有时会向下取整，表现出来就是1 个基准时钟周期的抖动。双边沿检测时，上升沿检测和下降沿检测其中一个是向上取整时，另一个一定是向下取整，两者取平均值就能将1 个基准时钟周期的误差降低一半。例如，当采用上升沿触发时，图2 所示中上升沿检测的基准时钟周期数是3 个，下降沿检测的基准时钟周期数是4 个，取平均值是3.5 个周期。

2.3 改进的双边沿检测测频算法

在实际测试中发现，只采用被测信号的双边沿测频算法不能达到测量精度提升一倍的效果，原因可能是基准频率由FPGA 的PLL 模块倍频产生，会引入额外的抖动，另外，被测频率也存在一定的抖动。

解决措施为在被测信号双边沿检测的基础上，加入基准频率信号的双边沿检测。具体做法为在被测信号上升沿触发的模式下对被测信号进行双边沿检测得到频率fx_rising和fx_falling，同时在基准信号下降沿触发的模式下对被测信号进行双边沿检测得到频率fx_rising和fx_falling，最终被测信号fx为

在上述双边沿检测测频算法的基础上，通过将闸门时间延时一个被测信号周期，可以进一步提高测频精度。将实际闸门开启时间定为被测信号第一个上升沿时，通过上述双边沿测频算法得到被测信号频率fx1；同时，将实际闸门开启时间延时一个被测信号周期，通过上述双边沿测频算法得到被测信号频率fx2。最终被测信号fx为

一般地，实际闸门时间为被测信号周期的整数倍，会小于采样间隔，将闸门延时一个被测信号周期后，实际测频周期会超过采样间隔，但误差不会超过一个被测信号周期，可以忽略。

3 试验与结论

对某频率输出传感器，用单边沿测频、双边沿检测、延时闸门等各种测频算法以及安捷伦频率计53220A 进行测频，用ALLAN 方差分析方法对结果进行分析[2]。以下测频结果均为相对频率测量精度，采样时间为5ms。

3.1 频率计测频结果分析

对某频率输出传感器，用安捷伦频率计53220A 进行测频，闸门时间选择5ms，结果用ALLAN 方差进行分析，如图3 所示。

频率计测频数据在高频段主要表现为白噪声，0.005s 和1s 的相对频率精度分别为9.3e-8 和4.7e-9；相对频率的不稳定性（即ALLAN 方差双对数曲线斜率为0 处）为2.3e-9，但响应速度慢，要超过10s 才能达到该指标。

3.2 单边沿检测测频算法结果分析

单边沿检测测频结果的ALLAN 方差分析如图4 所示。

和频率计测频数据不同的是，单边沿测频数据在高频段主要表现为量化噪声，0.005s 和1s 的相对频率精度分别为3.4e-7 和1.9e-9；相对频率不稳定性为4.6e-9。

3.3 双边沿检测测频算法结果分析

双边沿检测测频结果的ALLAN 方差分析如图5 所示。

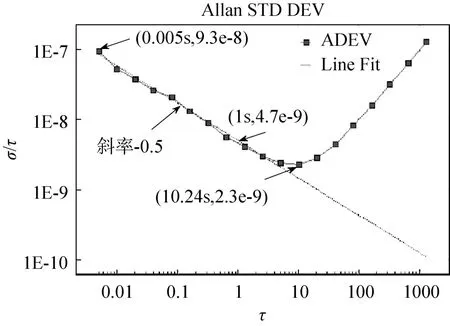
图3 安捷伦频率计测频结果ALLAN 方差分析Fig.3 Allan variance of frequency counting based on Agilent frequency counter

图4 单边沿测频结果ALLAN 方差分析Fig.4 Allan variance of frequency counting based on single-edge detection

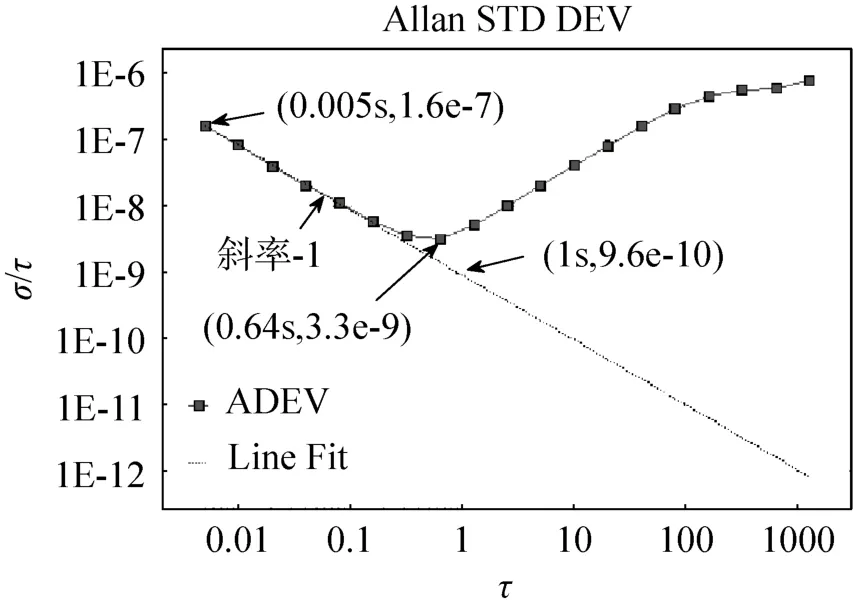
图5 双边沿测频结果ALLAN 方差分析Fig.5 Allan variance of frequency counting based on double-edge detection

双边沿测频数据在高频段主要表现为量化噪声，0.005s 和1s 的相对频率精度分别为1.6e-7 和9.6e-10，均为单边沿测频精度的一半；相对频率不稳定性为3.3e-9，和单边沿测频结果对比也有改善。

3.4 闸门延时测频算法结果分析

闸门延时测频结果的ALLAN 方差分析如图6 所示。

闸门延时测频数据在高频段主要表现为量化噪声，0.005s 和1s 的相对频率精度分别为1.2e-7和7.1e-10，和双边沿测频数据相比有改善；相对频率不稳定性为3e-9，和双边沿测频结果对比稍有改善。

图6 闸门延时测频结果ALLAN 方差分析Fig.6 Allan variance of frequency counting based on delayed sampling interval

3.5 总结

将各种测频方法的结果总结，如表1 所示。

表1 各种测频方法结果汇总Table 1 Allan variance measured by various frequency counting method

频率计和基于FPGA 的等精度测频的数据在高频段的噪声表现形式不同，前者表现为白噪声，后者表现为量化噪声。5ms 处的ALLAN 方差，FPGA 测频方案比频率计稍差；1s 处的ALLAN 方差，FPGA 测频方案远优于频率计；不稳定性，频率计稍优于FPGA 测频方案，但频率计测试时间超过了10s，FPGA 测频方案均不到1s。

基于FPGA 的高精度测频方案和频率计测频方案相比测频精度在同一量级。

4 结束语

基于FPGA 的高精度测频方案满足谐振式传感器的应用需求，且体积小、功耗低、易于多路扩展、算法灵活易于移植。另外，该方案也为ASIC 电路的研制提供了参考。