基于摩尔-库仑理论的沥青混合料抗剪强度研究

谢祥雄 李丽民 唐 琪 彭添柱 罗 成

（湖南科技学院 土木与环境工程学院，湖南 永州 425199）

随着超载、重载和交通量的增加，我国沥青路面车辙破坏日益严重。为解决路面的车辙问题，国内开展了大量研究。李丽民等[1-4]对抗车辙级配、车辙性能影响因素、路面车辙性能及剪应变影响规律等进行了研究。李文良[5]对沥青路面的车辙预估问题进行了研究。董泽蛟等[6]研究了沥青路面结构的抗车辙性能。以上这些研究都是从沥青混合料的高温性能和路面结构等方面对沥青路面抗车辙性能进行研究。实际上，路面的车辙破坏是剪切破坏，基于摩尔-库仑理论研究沥青路面的抗剪强度，是一种解决路面车辙破坏问题更为有效的方法。张慧鲜[7]从抗剪强度的角度研究沥青混合料高温性能的影响因素，并提出了相应解决措施。吴帮伟等[8]从抗剪强度的角度研究了沥青混合料高温性能，得到了车辙变形的产生机理与主要影响因素。这些研究获得了不少新的成果，但基于抗剪性能，对沥青混合料级配高温性能的研究不多，有待进一步深入研究。为此，基于土力学中摩尔-库仑理论，从级配角度对沥青混合料的抗剪强度能进行研究是十分必要的。

1 试验材料

试验采用级配见图1 和表1。为研究级配对沥青混合料抗剪强度的影响，对试验级配的分维数D 进行计算，得到1#，2#，3#的分维数D 分别为2.4507，2.4569，2.5171。沥青采用SBS 改性沥青，其性能指标见表2，粗、细集料采用石灰岩，矿粉采用磨细的石灰粉，各项指标检测均满足规定要求。

图1 试验用级配

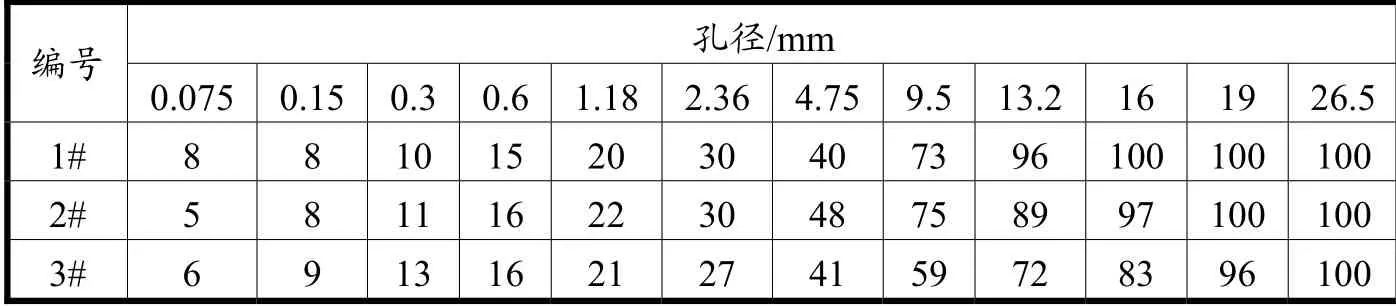
表1 试验用级配的筛孔通过率 单位：%

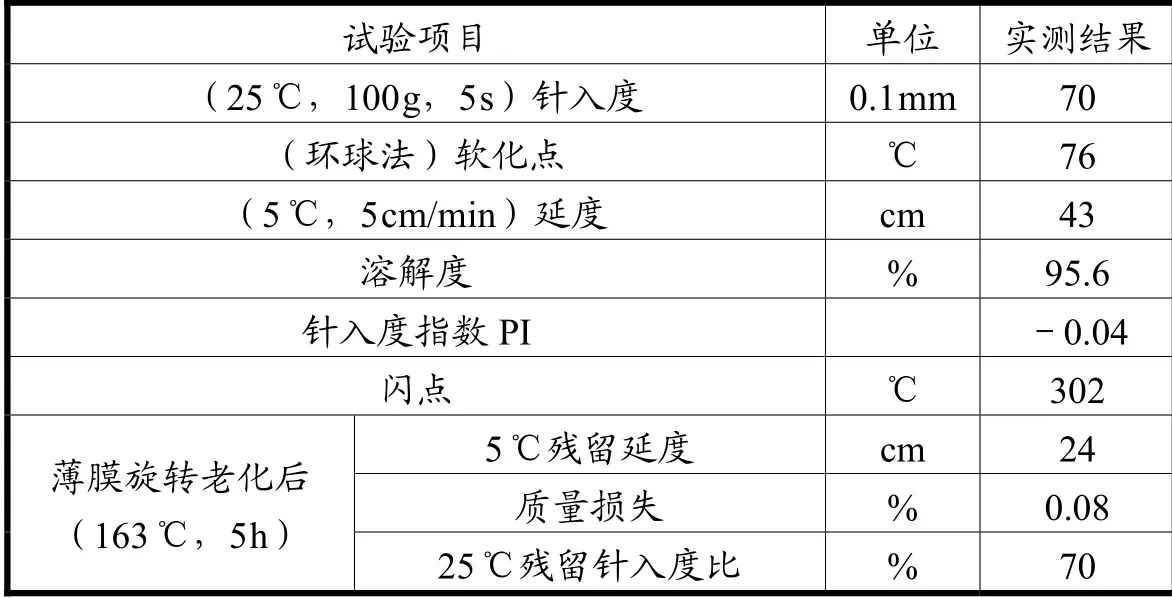
表2 SBS 沥青性能指标

对三种试验级配采用马歇尔法确定沥青混合料的最佳油石比。根据土力学中摩尔-库仑理论τf= c+σ tanφ ，如图2 所示，式中τf为抗剪强度，c 为黏聚力，φ 为内摩擦角，σ 为正应力，可知沥青混合料的抗剪强度取决于黏聚力c 和内摩擦角φ 。为得到沥青混合料的c 和φ ，根据图2，对每种级配最佳油石比的沥青混合料进行劈裂试验和无侧限抗压强度试验，得到劈裂试验应力圆和无侧限抗压强度试验应力圆，做两圆的公切线，根据式(1)和式(2)计算便得到沥青混合料的抗剪强度两个指标参数c 和φ[7]。

2 沥青混合料抗剪强度

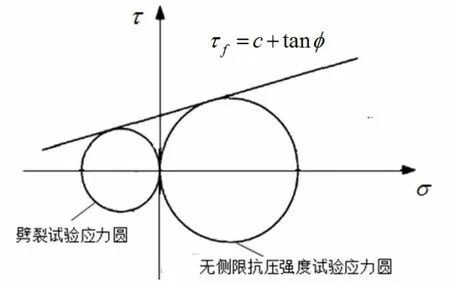
图2 土力学中摩尔-库仑理论

式(1)和式(2)中：1σ 为间接抗拉强度，pσ 为抗压强度。进行无侧限抗压强度试验、劈裂试验、车辙试验，表1 中三种样品的车辙深度、间接抗拉强度1σ 、抗压强度 pσ 的试验结果见表3。根据式(1)和式(2)计算得到级配的抗剪强度指标参数c 和φ ，结果见表3。对试验结果进行计算，级配分维数与内摩擦角、内摩擦角与车辙深度、级配分维数与车辙深度、级配分维数与黏聚力以及黏聚力与车辙深度的线性相关性结果见图3～图7。

表3 三种试验级配试验结果

图3 级配分维数与内摩擦角

图5 级配分维数与车辙深度

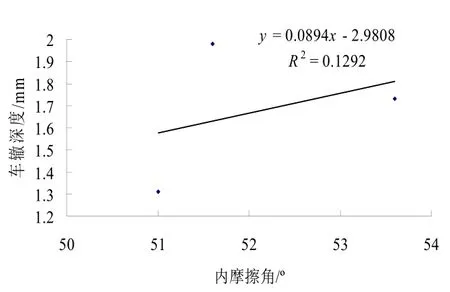
图4 内摩擦角与车辙深度

图6 级配分维数与黏聚力

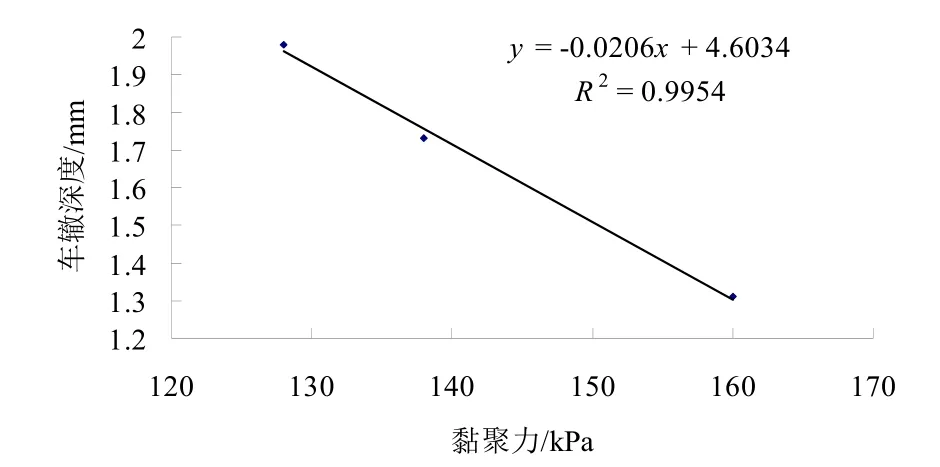
图7 黏聚力与车辙深度

图3 表明级配分维数D 与沥青混合料的内摩擦角相关性较差。从图4 可以看出沥青混合料的内摩擦角与沥青混合料的车辙深度相关性也较差，内摩擦角对沥青混合料的抗剪强度影响较小。图5 和图6 表明级配的分维数D 与沥青混合料的车辙深度及黏聚力有很好的线性相关性。从图7 可以看出黏聚力与沥青混合料的车辙深度也有很好的线性相关性，沥青混合料的黏聚力c 直接影响沥青混合料的抗剪强度。级配的分维数D 能很好地反应沥青混合料的抗剪强度，从抗车辙性能选择沥青混合料的级配时，可以从级配的分维数D 入手，通过车辙试验和维数D 进行级配的优选，级配的分维数D 可以作为沥青混合料级配抗剪强度的评价指标。

3 结 语

（1）级配的分维数D 与沥青混合料的车辙深度有良好的线性关系，级配的分维数D 与黏聚力也有良好的线性关系，级配的分维数D 能用作沥青混合料抗剪强度的表征指标。

（2）沥青混合料的内摩擦角与级配的分维数D 性相关性不强，沥青混合料的内摩擦角与车辙深度线性相关性也不强，沥青混合料的内摩擦角对沥青混合料的抗剪强度影响不如黏聚力明显。

（3）研究只采用了单一沥青，并且采用的级配不多，今后应进行更多沥青和级配的沥青混合料的抗剪强度的深入研究，并通过实体工程进行验证。