巧用符号表征过程 构建模型提升素养

马骏 鲁艺

[摘要]感悟建模过程、发展模型思想是提升学生核心素养，促成深度学习的重要方式之一。小学数学建模的教学可归纳为四个步骤：模型准备、模型假设、模型构成、检验应用。四个步骤相辅相成、缺一不可。

[关键词]小学数学;倒水问题;数学模型;数学语言

[中图分类号]

G623.5

[文献标识码]A

[文章编号] 1007-9068（ 2020）29-0023-03

“倒水问题”是一类典型的运用丢番图方程进行解答的问题。在小学阶段，倒水问题的教学往往被两点所困扰，一是如何简明直观地向学生呈现倒水的各项操作过程，二是如何引导他们剖析其中的过程并找出解题之法。笔者从芬兰“无电脑编程”的算法思维教学中得到启示，参考西南师范大学出版社出版的《数学文化》五年级下册的“分饮料”一课，从培養学生的模型思想出发，设计了相应的数学文化课例。

一、模型准备——根据问题，构建符号表征系统

数学模型是应用具象化数学语言来表现抽象化数学知识的方式。因此，构建数学模型首先要充分收集并整理相关信息，在学生了解了这一类问题的基础上，探索用更简单明了的方式来描述。

（例1：现有一大一小两个水桶，但都没有刻度，大桶能盛放5L水，小桶能盛放4L水，假设现在有无限多的水，请问如何才能通过这一大一小两个桶准确得到3L水呢？）

生1：先把小桶灌满水，然后倒入大桶，大桶里就有4L水。再把小桶灌满水，接着往大桶里倒，直到大桶灌满（即大桶里倒入了1L水），这时小桶里就有3L水。

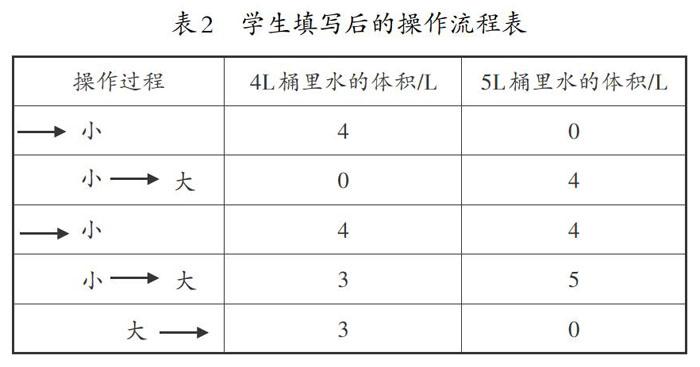
师：这里有一个表格（如表1），大家能不能用一种简单明了的方法来展示每一步的操作过程呢？

生2：可以用“一小”表示把小桶接满水，用“小一大”表示把小桶的水倒给大桶，用“大一”表示把大桶里的水倒出去。

师：请同学们根据自己设计的方法来填写。

师：一大一小两个桶的倒水问题，还可能会出现哪几种操作？

生3：除了上面三种外，还有“→大”“大→小”和“小→”。

师：如果把一大一小两个桶看成一个整体，这六种操作可以分为几类？

生4：分为三类。一是进水，总水量增加;二是水从一个桶到另一个桶，总水量不变;三是把水倒出去，总水量减少。

师：水从一个桶到另一个桶，总水量不变，我们可以称为内部操作;另外两类总水量发生变化，我们可以称为外部操作。

在模型准备阶段，需要给予学生充分的空间，使他们初步认识、感知这类问题，发挥创作才能，设计出符合自身认知的符号化语言。接着，让学生在教师的引导下，对操作进行分类，为下一步的模型假设和构成奠定基础。

二、模型假设——简化过程，分析提炼内涵规律

模型假设是将收集到的信息进行简化的过程，要抓住其主要矛盾，忽略无关信息的影响。在教学过程中，要充分利用模型准备阶段所确立的表征系统，丰富学生对于倒水问题的感受，再从内部操作和外部操作两个维度来简化问题。

师：将上面的题目稍加修改，变成一个新问题。

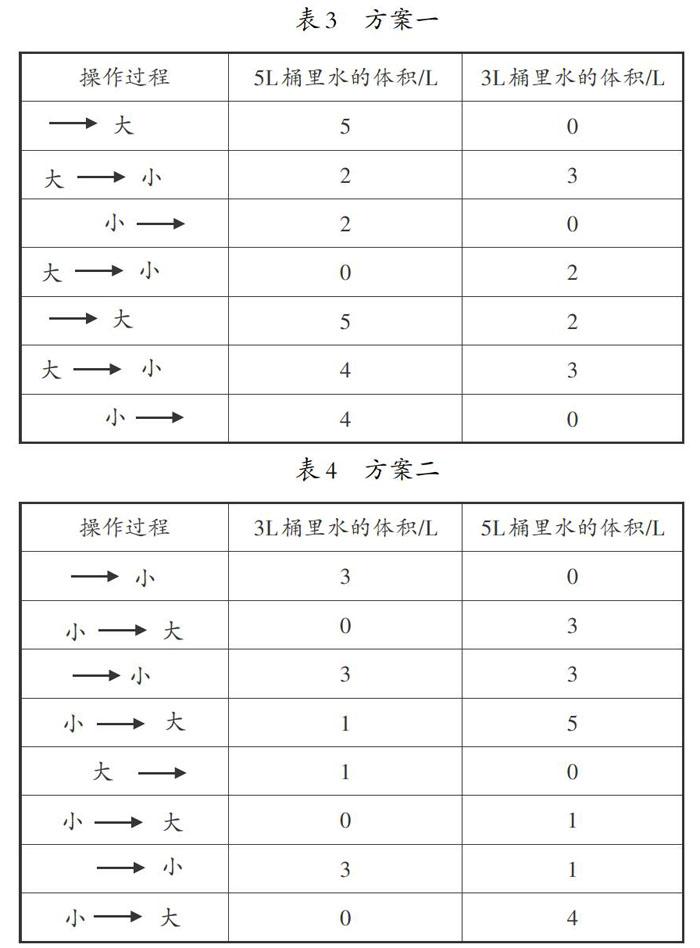
（例2：现有一大一小两个水桶，但都没有刻度，大桶能盛放5L水，小桶能盛放3L水，假设现在有无限多的水，请问如何才能通过这一大一小两个桶准确得到4L水呢？）学生方案如下：

师：请仔细观察表3、表4，说说你有什么发现？

生1：我发现方案一的水都是从大桶到小桶，方案二的水都是从小桶到大桶。也就是说，每种方案的内部操作只有一种。

师：真棒！刚才研究了内部操作，那外部操作呢？又有什么发现？

生2：我发现，同一个方案里，一个桶只负责进水，另一个桶只负责倒水。

师：为了方便起见，我们把进水的桶称为1号桶，倒水的桶称为2号桶。在同一个方案里，内部操作是从1号桶到2号桶，水的流向是单一的;外部操作都是从1号桶进，2号桶出，功能唯一。

通过对两种方案的对比分析，从看似繁杂的步骤中捕捉共同点，逐渐梳理出内部操作和外部操作规律的唯一性，从高处着眼，总结并简化了问题的操作步骤。

三、模型构成——建立联系，数学语言概括表达

教师需引导学生利用数学工具来描述信息以及信息中各种对象之间的关系，逐步串联起内部操作和外部操作，透过现象看本质，从局部跃迁到整体，建构出数学模型。

师：回顾一下，无论是哪个方案，第一步是什么操作？第二步呢？

生1：第一步是外部操作，第二步是内部操作，第三步又是外部操作，第四步又是内部操作……内外部操作交替进行。

师：观察方案一，第一步给1号桶装满水，第二步将水从1号桶倒入2号桶里，如果2号桶里的水没装满，看看下面又是什么操作？

生2：继续给1号桶装满水，再往2号桶里倒。

师：如果2号桶的水装满了，还没得到想要的4L水，这时该怎么办？

生3：把2号桶里的水倒掉，然后把1号桶里剩下的水倒入2号桶。

师：再继续看剩下的步骤，你有什么发现？

生4：剩下的操作其实一直在重复之前的步骤，直到出现4L水。其实当1号桶确定之后，整个操作一直在重复如图1所示的步骤。因此，只要明确1号桶进几次水，2号桶倒几次水，中间的步骤就按照2号桶已满和未满两种情况来处理，直到得到4L水。

师：按生4所说，只看外部操作和最后结果（如表5），你有什么发现？

生5：我列了一个算式3x3-5x1=4，其中“3x3”表示3L的桶进水3次，“5X1”表示5L的桶倒水1次。

师：用同样的方法，你们能给方案一也列出一个这样的算式吗？

生6：5x2-3x2=4，其中“5x2”表示5L的桶进水2次，“3x2”表示3L的桶倒水2次。

师：我们可以总结出“进水桶的容积×进水次数一倒水桶的容积×倒水次数=目标体积”的公式。

以问题为引导，结合板书，以数形结合的形式启发学生观察并梳理其中所蕴含的规律，得出倒水问题其实是在交替进行内外部操作，两种操作是非此即彼的关系。因此，只需将目光聚焦于外部操作，就可以把整个过程用数学算式表示出来，并在此基础上进一步总结出数量关系式，得出数学模型。

四、检验应用——投入实践，内化模型推广延伸

模型思想是一种高层次的数学思维方式。在应用形象化的数学语言将相对抽象的数量关系初步描述之后，再对模型进行检验并利用模型求解，完成从理论到实践的跨越，这也是数学学科严谨性和实用性的体现。

师：总结得到的这个数量关系式有什么用途呢？

生1：可以根据数量关系式，列算式并算出进水次数和倒水次数，进而解决倒水问题。

师：那就按照大家的说法来试一试，看可不可行。

（例3：现有容积为7L和11L的桶各一个，但都没有刻度，假设现在有无限多的水，想要准确量出IOL水，你会怎么办？）

生2：经过尝试，我发现选择7L的桶来进水比较容易，算式是7x进水次数-11X倒水次数=10，进水3次，倒水1次，就能得到10L水，具体步骤如表6所示。

师：同学们，像倒水问题这样总是循环往复操作的问题，谁比较擅长呢？

生3：计算机。

师：没错！在生产中常使用计算机编程来解决类似的问题，而今天我们的研究思路和编程语言里的if语句不谋而合。

师：大家看，针对同一个问题，既可以用口头语言来叙述每个操作过程，也可用表格来展示，还可以用数学算式来表达。说到这里，你有什么感受吗？

生4：我觉得数学算式是其中最简单的表达方式。

师：这就是数学的简洁之美！

以上教学环节，先让学生验证模型的实用性，再将数学语言与编程语言相联系，拓宽了课堂的视野和格局，最后通过几种表达方式的对比，让学生体会到数学语言简洁的特点。

综上所述，模型思想是体现数学逻辑思维价值，提升学生数学素养，帮助人们掌握并发现事物本质，深层理解核心关键的重要思想方法。同样，以培养学生数学建模素养为驱动的教学设计也是实现课堂深度学习的重要方式，值得一线教师进行深耕。

（責编李琪琦）