远程导弹的自适应反步姿态控制系统设计

梅瀚桐，麻黎娟，吴光辉，邵 翔，许朋亚

(1. 西北工业大学航天学院，陕西 西安 710072； 2. 火箭军装备部驻北京地区第一军事代表室，北京 100076； 3. 上海机电工程研究所，上海 201109)

0 引 言

远程导弹飞行包线大，飞行特性在包线内快速大范围变化，飞行环境复杂多变，受到来自环境和敌方的各种干扰，远程导弹的控制精度会下降甚至失稳。另一方面，作为一个复杂的被控对象，随着其机动性能的提高，姿态控制系统具有高不确定性、强耦合、快时变以及强非线性等特征，传统的线性控制方法难以满足姿态控制系统对精确度和稳定性的要求[1]。近年来，各种非线性控制方法成为研究热点，如鲁棒控制[2]、滑模自适应控制、自抗扰控制[3]等，并取得了诸多进展。

王嫡[4]针对3个子系统分别设计了反步滑模变结构控制器，以解决导弹姿态控制中的全局鲁棒性问题。蒋瑞民等[5]针对存在非线性和不确定性的倾斜转弯导弹姿态控制问题，提出了基于干扰估计的鲁棒方差控制方法，将姿态运动中非线性项和不确定项作为总干扰，采用干扰观测器进行估计，并引入控制系统进行补偿，使得鲁棒方差姿态控制器能够保证良好的控制效果。丁力等[6]为了提高复杂干扰情况下的姿态稳定控制，设计了一种自抗扰无源控制器，达成姿态控制和有效抑制外部干扰的目的，提高了控制精度和系统的鲁棒性。文献[7]针对范数有界的不确定性和有界连续的未知干扰，通过设计一个滑模状态观测器和一个自适应参数估计器，基于获得的状态估计值和未知参数估计值，提出了一种基于自适应动态面的跟踪控制律，通过仿真证明了自适应滑模动态面控制策略具有更好的跟踪效果。唐硕[8]引入自抗扰控制器(active disturbance rejection controller，ADRC)技术，并针对飞行减载控制对其进行改进，不仅通过状态观测器将误差补偿引入自抗扰回路，还改进了自抗扰控制器中的控制律，给出了控制方程中增益的选择方法，证明了系统的稳定性，提高了系统的鲁棒性。常怡鹏等[3]设计了一款基于神经网络在线补偿动态逆误差的控制器，为降低导弹的强非线性以及强耦合性，采用两个回路相应的姿态控制器以及神经网络在线补偿逆误差的方法，以提高控制系统的鲁棒性。荆家玮等[9]在参数时变不确定的条件下，面向具有故障的制导火箭执行机构，采用基于神经网络观测器的故障估计方法设计了一种鲁棒自适应容错补偿控制器。

为了提高复杂干扰情况下的姿态控制精度，本文提出了一种自适应反步姿态控制器。首先，建立了远程导弹的模型，为了避免姿态奇异问题，将基于欧拉角的模型转化为基于四元数的刚体运动学模型；然后，在此基础上设计了一种自适应反步姿态控制器，对外界干扰进行自适应估计和补偿，并基于Lyapunov函数方法证明了系统的稳定性；最后，通过仿真验证了本文所提方法的有效性。

1 姿态控制系统状态空间模型建立

远程导弹的运动是刚体运动和非刚体运动高度耦合的复合运动，其中刚体运动是导弹的基本运动，控制系统的主要任务就是控制刚体运动并抑制非刚体运动。本文主要讨论远程导弹的姿态控制，因此重点研究绕3个惯量主轴的角度运动，并忽略质心运动参数偏差对绕质心运动的影响。本文假设远程导弹飞行过程中的弹性变形位移及转角较小，动力学建模忽略导弹的非刚体运动，将远程导弹简化为刚体，其质心位置不发生改变，同时忽略结构参数误差(如质量和惯量偏差等)对干扰运动的影响，也不考虑高度对气动系数和推力的影响。

定义研究对象的四个芯级发动机分别为Cj(j=1,2,3,4)，对应的发动机摆角为δj(j=1,2,3,4)，rc代表芯级发动机的摆动喷管距离导弹轴向中心线的距离。本文假设发动机的各个推力大小一致，即P1=P2=P3=P4。导弹的发动机摆角示意如图1所示，摆角幅值限制为±18°。

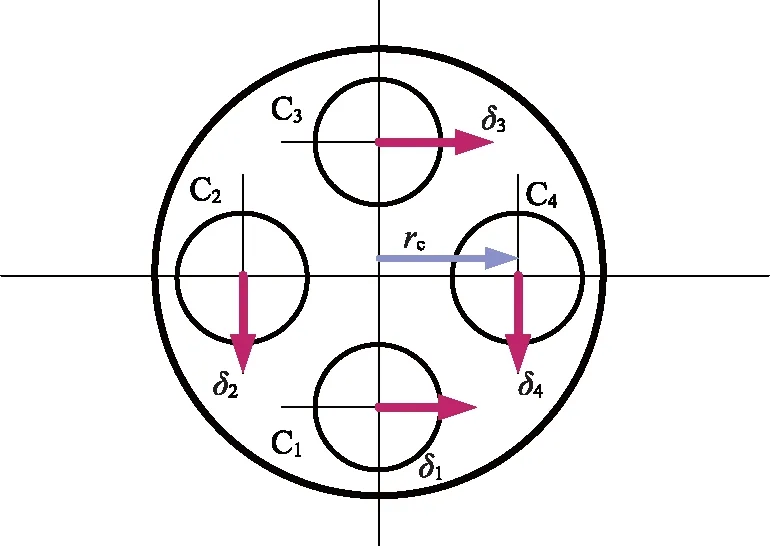
图1 导弹的发动机摆角示意图Fig.1 The engine swing angle of the missile

1.1 基于欧拉角的导弹运动学动力学模型

根据导弹绕质心转动动力学方程和导弹的运动学方程，定义如式(1)所示的状态变量。

(1)

式中：状态变量X0代表描述弹体坐标系相对导航坐标系的姿态角(俯仰角φT、偏航角ψT、滚转角γT)；状态变量X2是在弹体坐标系中表达的系统相对导航坐标系的角速度矢量(滚转角速度ωTx1、偏航角速度ωTy1、俯仰角速度ωTz1)。

根据导弹的姿态运动学方程和姿态动力学方程，建立基于欧拉角的远程导弹运动方程组，如式(2)所示。

(2)

式中：

f=MRst+MRD+Mδ+M′k；

式中：J是弹体坐标系中的惯量张量式；u是输入的摆角矩阵；B是控制分配矩阵，xR为芯级发动机铰链点位置距导弹弹体理论尖端的距离，xg为导弹质心距导弹弹体尖点的距离；f是系统的非线性项力矩，MRst是气动稳定力矩，MRD是气动阻尼力矩，Mδ是发动机摆动惯性力矩，M′k是附加哥氏力矩；dext是模型的干扰力矩，MB是导弹力学环境中的结构干扰力矩或其他外部干扰力矩。

1.2 基于四元数的导弹运动学动力学模型

采用姿态角描述运动模型，无法保证从坐标转换矩阵求出唯一姿态角φT、ψT、γT的性质，即存在欧拉角的奇异性。为了统一导弹飞行的动力学模型并避免姿态角奇异，远程导弹在空间运动中一般采用四元数进行姿态描述。因此，本文对四元数的姿态描述方法进行讨论，进而完成基于四元数的控制系统设计。

重新定义基于标准四元数的状态变量X1为

X1=[q1q2q3q0]T=[qTq0]T

(3)

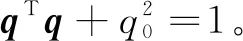
在式(2)的基础上，得到面向标称状态的执行机构，基于四元数的导弹运动学模型为

(4)

式中：

现定义矩阵S(x)∈R3×3是一个斜对称矩阵，且满足对于任意矢量x,y∈R3，S(x)y=x×y。则S(q)可以表达为

(5)

将式(5)代入式(4)，整理得到基于四元数的导弹刚体运动学模型为

(6)

式中：I3为3×3的单位矩阵。

2 自适应反步姿态控制方法

2.1 姿态跟踪误差动态方程

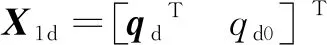
姿态跟踪误差X1e被定义为

(7)

角速度误差X2e可以被描述为

X2e=X2-R(X1e)X2d

(8)

式中：X2d是弹体坐标系下的期望角速度；R(X1e)为姿态转移矩阵。

姿态转移矩阵R(X1e)被定义为

R(X1e)=(qe02-qeTqe)I3+2qeqeT-2qe0S(qe)

(9)

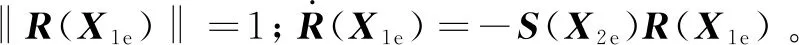
因此，姿控系统的姿态跟踪误差动态方程可以用式(10)描述，即

(10)

本文的控制目标是在远程导弹存在外部干扰的情况下，设计自适应反步姿态控制器，实现精确的姿态稳定和跟踪。为了证明所提方法的稳定性，提出以下合理假设：

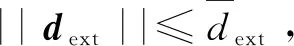
2.2 自适应反步姿态控制律设计

设计内环虚拟控制律为

X2e,virtual=-kqe

(11)

式中，k是一个待设计的参数，k>0。

定义姿态角速度跟踪误差的估计误差为

(12)

设计包括非线性反馈项和自适应补偿控制律的外环理论控制律，表达为

(13)

d=dext

(14)

考虑以下l2最优控制分配问题[10]来计算理论控制输入u,即

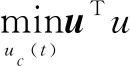
(15)

根据文献[11]，可以直接得到式(15)的求解，为

(16)

(17)

式中，η0为自适应更新率参数。

姿态角将会精确地收敛到期望值，从而实现精准的姿态跟踪。这个结果将在下一节中得到证明。

2.3 稳定性证明

我们将自适应参数估计误差定义为

(18)

式(18)等号两边同时对时间求导可得

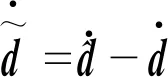
(19)

由式(10)～(16)，闭环系统的动态方程可以推导为

(20)

考虑一个Lyapunov函数候选，如式(21)所示。

(21)

显然，这个Lyapunov函数是正定的。

V1的导数为

(22)

结合式(20)中的第一个方程，可以得到

(23)

V2的导数是

(24)

再利用式(20)中的第二个方程，可以得到

(25)

将自适应参数更新律式(17)代入式(25)，再将其与式(23)合并，可得

(26)

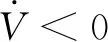
(27)

3 仿真及结果分析

为验证上述反步控制器的控制性能，首先选择某一特征点处数据进行单点测试仿真分析。

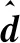
假设外部干扰dext=[0.1;0.1;0.1]。设计的控制增益与参数如表1所示。

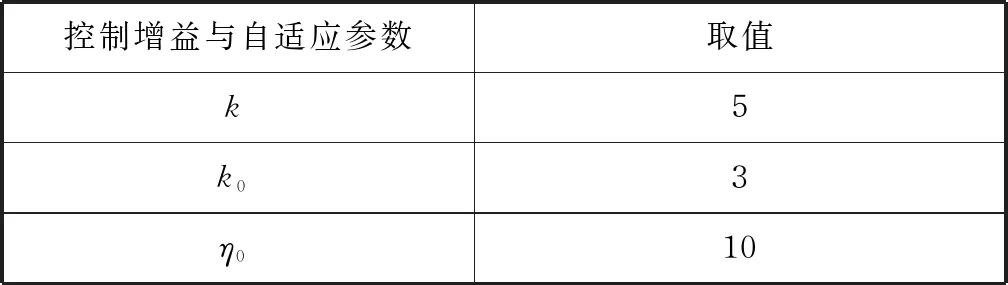
表1控制增益与自适应参数的设计Tab.1 Control gain and adaptive parameter design

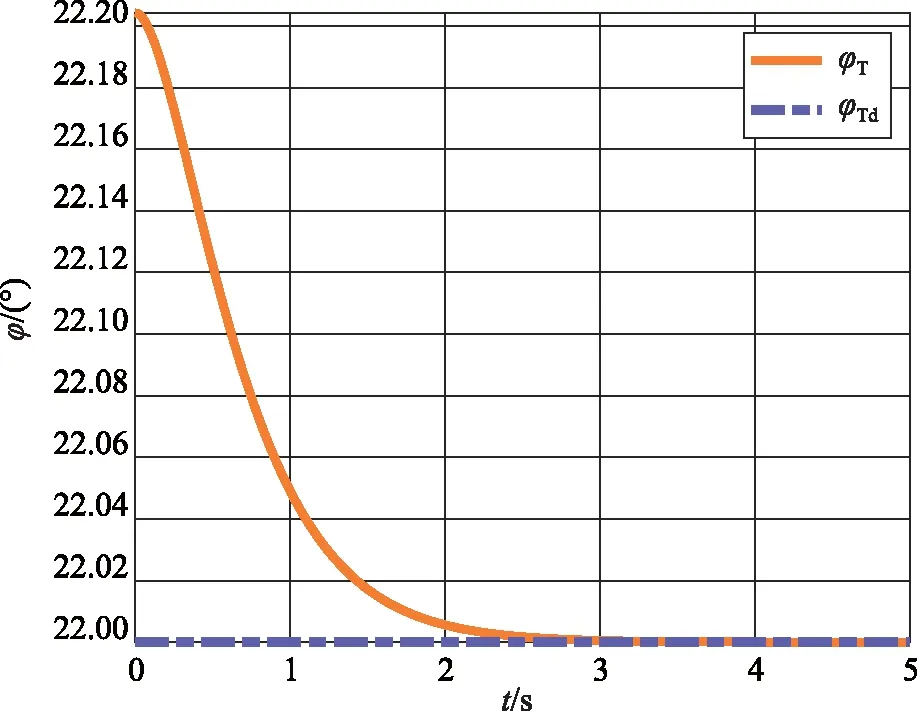
图2 俯仰角及期望俯仰角输出Fig.2 Pitch angle and expected pitch angle

图3 偏航角及期望偏航角输出Fig.3 Yaw angle and expected yaw angle

图4 滚转角及期望滚转角输出Fig.4 Roll angle and expected roll angle

图5 俯仰角速度及期望角速度输出Fig.5 Angular velocity and expected angular velocity of pitch

图6 偏航角速度及期望角速度输出Fig.6 Angular velocity and expected angular velocity of yaw

图7 滚转角速度及期望角速度输出Fig.7 Angular velocity and expected angular velocity of roll

图8 自适应参数输出Fig.8 Adaptive parameters

图9 舵偏角δ输出Fig.9 Rudder deflection angle δ

由图3～9可知，针对存在有界外部干扰的远程导弹，采用自适应反步姿态控制器可使导弹三轴的姿态角及角速度在3 s左右收敛，显示出优良的控制性能，可以保证导弹姿态稳定控制的要求。

4 结束语