基于滑模控制的多弹分布式视线协同制导律设计
赵 斌,黄晓阳,周 军,郭 玥
(西北工业大学精确制导与控制研究所,陕西 西安 710072)
0 引 言
近年来,受生物集群现象启发,个体协同控制研究受到广泛重视[1]。相比于传统单一系统执行任务模式,多分系统(个体)协同执行任务可以提高系统行为的智能化程度,从而完成单一系统无法完成的复杂任务[2]。在飞行器集群控制领域,协同制导律由于可降低成本并且可以通过信息交互使飞行器有效配合完成复杂飞行任务,已经受到广泛关注。协同制导已在无人机编队[3]、战术导弹集群[4]、卫星编队控制[5]等多个领域得到应用,涌现出大量成果。在协同制导与控制领域中,多智能体理论是主要的研究手段,其主要思想是通过智能体与相邻智能体之间的信息交互,不断调整自身的状态从而使所有智能体的某些状态实现一致性[6]。
基于多智能体一致性解决飞行器协同制导问题时,常见的协调变量有遭遇时间[7-12]、剩余距离与视线角[13-17]和速度[18-19]等。这些研究采用的数学模型主要是一阶和二阶质心运动学,以作用于质心的加速度为控制量。战术导弹末制导段通常进行无动力飞行,因此很难通过调整速度大小来实现遭遇时间、剩余距离以及速度等协同变量的一致,相比之下实现视线角的一致则是可行的方案。文献[20-21]针对平面运动目标,以脱靶量、相对视线角偏差和控制能量为性能指标,基于最优控制理论设计了协同制导律。文献[22]在平面比例导引基础上增加了视线角协同项,设计了一种视线角协同导引律。文献[14]提出了基于领弹-从弹的协同制导律。文献[7-17]针对固定目标设计多弹自主协同制导律。文献[17-19]提出了基于领弹-从弹拓扑的协同制导律,将目标视为“领弹”,弹群采用一阶一致性算法实现对目标的跟踪,从而把协同拦截问题转换为一致性跟踪问题。
以上研究的前提是将导弹运动模型简化为一阶或二阶运动模型,并且忽略重力、气动力等因素,采用的控制输入为质心过载加速度,而非对导弹进行飞行控制的舵偏角。然而,大气层内战术导弹在末制导阶段通常进行无动力飞行,通过舵偏角进行姿态调整以实现对需用过载的调节。因此,现有文献中的相关研究由于模型过于理想化,无法真正用于战术导弹末制导段的协同制导中。
针对此问题,本文对现有协同制导方法的数学模型进行了改进,将舵偏角作为控制输入,建立了考虑重力、气动力以及姿态变化的战术导弹协同制导模型,提出了一种二维纵向平面内的视线角一致协同制导算法。本文采用领弹-从弹的一致性协同策略,设计了稳定精度高、收敛速度快的分布式滑模制导律,其中,领弹采用有限时间收敛的滑模制导律结合干扰观测器以实现对机动目标的精确打击;从弹则在分布式的自适应连续化滑模控制协议下跟踪领弹对目标视线角,以实现目标的协同攻击。
相比于已有的协同制导律,本文所设计的分布式协同控制算法具有以下优点:①采用以舵偏角为控制输入的导弹飞行模型直接进行控制律的设计,更接近于实际的物理系统,具有良好的工程应用价值;②采用领弹-从弹的一致性协同策略,可以将领弹与从弹分开进行设计来实现对目标的协同攻击;③采用领弹-从弹结构,可以降低从弹弹载计算和对探测设备的要求,具有传递信息少、协调时间短等优势,节约了成本。
1 数学建模
本文考虑纵向平面内N枚从弹与一枚领弹协同攻击运动目标的场景。为方便描述,将第i枚导弹记作Mi,领弹记作M0,目标记作T。
考虑二维纵向平面内一枚领弹与多枚从弹对运动目标进行协同攻击。导弹Mi与目标的相对位置关系如图1所示,其中xoy为地面坐标系,vi表示导弹飞行速度,vT为目标飞行速度,ηi、qi分别表示导弹相对目标的速度偏向角与视线角,ηiT表示目标相对于导弹Mi的速度偏向角,ri为弹目距离。
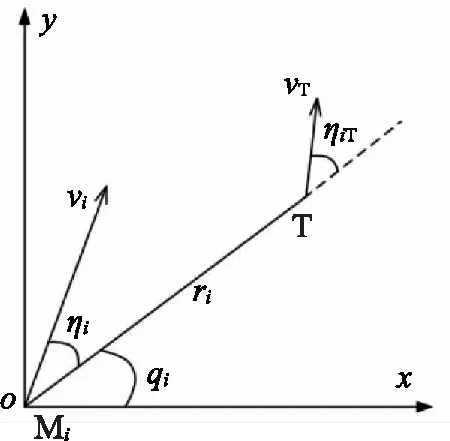
图1 导弹与目标相对运动关系Fig.1 Relative motion between missile and target
根据图1可以建立导弹Mi运动方程以及弹-目相对运动模型为
(1)

(2)
1) 领弹制导模型
(3)
式中:g(t)为模型不确定性;aM为导弹加速度。
2) 从弹制导模型
基于式(1)所示模型,对视线角进行二阶微分可得从弹制导模型为
(4)


(5)
式中:ζ1=rmaxg;ζ2=2vmax;rmax表示飞行过程从弹与目标的最大距离;vmax表示从弹的最大速度。
(3) 领弹-从弹通讯拓扑
对于一枚领弹与多枚从弹构成的协同制导体制,用G=(V,ε)表示其通讯拓扑结构,其中V={1,2,...,N}为导弹节点构成的集合,ε⊆V×V表示导弹间的通讯链路构成的集合,记矩阵A=[aij], 1≤i,j≤N为该通讯拓扑结构图的邻接矩阵,记矩阵L=[lij](1≤i,j≤N)为该通讯拓扑结构图的Laplace矩阵。图2给出通讯拓扑结构的示意图。

图 2 导弹组网通讯拓扑结构图Fig.2 Communication topology structure of missile networking
2 引理及定义
基于式(4)所示模型,给出领弹-从弹制导体制中关于视线角渐近协同追踪的定义。

为进一步解决视线角的协同追踪问题,在式(4)所示模型的基础上定义集总追踪误差
(6)
式中:lij∈L(i,j=1,...,N),L为从弹间的通讯拓扑图的Laplacian矩阵;bi(i=1,2,...,N)表示领弹与从弹之间的通讯拓扑,如果bi=0,则表示第i枚从弹接收不到领弹的视线角信息,若bi=1,则表示第i枚从弹可以接收到领弹的视线角信息。

(7)
定义
(8)
因此集总误差系统的动力学形式可表示为
(9)
当领弹与从弹构成的通讯拓扑结构图存在一个有向生成树时,L+B是可逆矩阵[23]。根据式(6)可知,各从弹的视线角跟踪误差都收敛到0等效于集总误差收敛到0。故有如下引理:
引理1[24]:如果由式(3)表示的领弹-从弹模型下的通讯拓扑结构含有一个有向生成树,则由式(3)表示的领弹-从弹系统的视线角渐近(或最终有界一致)协同追踪问题等效于由式(7)表示的集总误差系统的渐近(或最终一致有界)稳定问题。
为方便后续证明,引入下列引理。
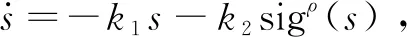
(10)
引理3[26]:考虑一阶的单输入单输出非线性系统

(11)
式(11)表示沿系统轨线的滑模动态特性。s=0定义了系统在滑模面上的运动;u∈R为连续控制输入;g(t)为充分光滑的不确定函数且m-1次可微;gm-1(t)具有已知Lipschitz常数L。针对该模型,引出非齐次干扰观测器
(12)
式(12)中,函数hi可表示为
(13)
式中:λi>0,μi>0,i=0,1,...,m。
假设式(11)所示系统中的s(t)和u(t)可以测量得到,所对应的参数λi、μi在逆序上充分大,则系统状态经历有限时间的暂态过程后,将满足
z0=s(t),z1=g(t),…,zi=vi-1=g(i-1),i=1,…,m
(14)
引理4[27]:考虑时变信号y(t)满足
(15)
其中,f(y(t),t)对y(t)满足Lipschitz条件,对所有t≥0连续。如果连续函数x(t)的上右导数在t∈[t0,T)时满足微分不等式
D+x(t)≤f(x(t),t),x(t0)≤y0
(16)
则对所有t∈[t0,T0),均有x(t)≤y(t)。
3 领弹滑模制导律设计
针对式(3)所示系统,选取有限时间收敛的滑模面
(17)
式中:td>t为期望的滑模收敛时间;n>1为设计参数。为使td>t,取td=tf,tf为领弹攻击目标的结束时刻。于是td-t=tf-t=tgo为剩余飞行时间,取
(18)
对式(3)所示系统中的不确定干扰项g(t),根据引理3设计非线性齐次干扰观测器进行估计。
(19)
基于式(2)系统、式(13)滑模面以及式(19)干扰观测器,直接给出领弹控制过载aM的表达式如下
(20)
定理1: 考虑到式(3)所示领弹的制导模型,在式(20)的控制过载下,领弹可以实现在给定视线角约束下对运动目标的精确打击。
证明:对所选取的式(17)滑模面进行求导,可得

(21)
将式(20)代入式(21)中,可得
=-k1s-k2sigρ(s)
(22)

(23)
即
(24)
(25)
进一步有
(26)

因此理论上可以证明该导引律能够在有限时间内使得领弹在视线角约束下击中目标。
4 从弹分布式协同制导律设计
基于集总追踪误差系统模型(式(6)所示)选取滑模面为
si=μe1i+e2i,i=1,2,...,N
(27)
其中,μ>0。将N个从弹滑模写为向量形式
s=μe1+e2,s=[s1,s2,...,sN]T
(28)

在式(28)滑模面与式(4)模型基础上直接给出以舵偏角为控制输入的从弹Mi的制导律为
(29)
式中:
(30)
式中:ξ>0;βi由式(31)自适应律给出。
(31)
式中:χ>0;γ>0。定义
(32)
得到紧凑形式
aδz=(L+B)-1(-μe2+b⊗aM+g(s))-aα
(33)
定理2:考虑到式(4)领弹-从弹系统模型,在式(29)自适应连续化滑模追踪算法下,从弹可以实现对领弹视线角的一致有界协同追踪。
证明:首先证明式(28)定义的滑模变量可以在有限时间内到达滑模面的一个边界层。
考虑Lyapunov函数
(34)

对式(34)求微分并结合式(9)可得
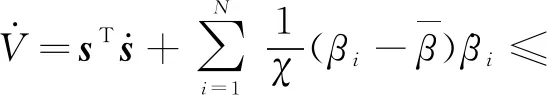
(35)


情况1: ∀i=1,2,...,N,βi‖si‖≥ξ,由式(30)得
(36)

情况2:若∀i=1,2,...,N,βi‖si‖<ξ,由式(30)得
-β0‖s‖+η2
(37)
式中,η2=η1+Nξ/4
情况3:如果一部分从弹节点满足βi‖si‖<ξ,另一部分从弹节点满足βi‖si‖≥ξ,则结合情况1与情况2,可以得到
(38)
综合上述情况,对任意βi‖si‖(i=1,2,...,N),有
(39)

(40)
下面证明式(4)领弹-从弹模型能够在式(29)自适应连续化滑模控制协议下实现视线角的最终一致有界追踪问题。在式(40)边界层内有
(41)

(42)
式中,0<θ1<1。所以式(6)追踪误差系统的轨迹能够在有限时间内到达式(43)边界内。
(43)
综上可知,式(6)追踪误差系统最终有界。根据引理1,式(4)领弹-从弹模型能够在式(29)自适应连续化滑模控制协议下实现视线角的最终一致有界追踪。
5 数学仿真与分析
设有5枚战术导弹对一匀速运动目标进行协同攻击,其中包含1枚领弹与4枚从弹。领弹的制导律参数及观测器参数如表1、表3所示,4枚从弹制导律参数、初始状态如表2、表4所示,领弹与目标的初始状态如表5所示,领弹的理想弹道倾角qd=0.5rad。

表1 领弹制导律参数Tab.1 Parameters of the leader’s guidance law

表2 从弹制导律参数Tab.2 Parameters of the followers’ guidance law

表3 干扰观测器参数Tab.3 Parameters of the disturbance observer

表4 各从弹初始条件Tab.4 Initial conditions of the followers

表5 领弹与目标初始条件Tab.5 Initial conditions of the Leader and Target
领弹与从弹间的通讯拓扑如图3所示,领弹采用有限时间收敛制导律结合干扰观测器对目标进行攻击,从弹则在分布式的自适应连续化滑模控制协议下追踪领弹的视线角以实现对目标的协同攻击。仿真结果如图4~5所示。

图 3 仿真实例中的多弹通讯拓扑结构图Fig.3 Communication topology structure of missiles in simulation

图4 场景1下的仿真结果Fig.4 Simulation results in scenario 1

图5 场景2下的仿真结果Fig.5 Simulation results in scenario 2
场景1:无气动拉偏。从图4中可以看出,各从弹与领弹飞行状态稳定,其控制舵偏角以及攻角、弹道倾角满足实际物理系统需求,并且在所设计的舵偏控制输入下,被控从弹可以对领弹视线角进行有效跟踪,并最终跟踪至领弹约束视线角从而实现对目标的精确协同攻击。
场景2:考虑20%气动拉偏。从图5中可以看出整个飞行过程仍然是稳定的。虽然对领弹视线角的跟踪效果相比于无拉偏情况存在一定的偏差,但误差仍然在可以容忍的合理范围内,并且各从弹在所设计的舵偏控制输入下与领弹一同趋向于理想的视线角命中目标,实现了良好的协同攻击效果。
综合以上仿真分析,可以验证所设计的领弹-从弹协同制导律的有效性,证明其能够实现对目标的协同有效打击。
5 结束语
针对多导弹集群分布式协同目标打击问题,本文以舵偏角为控制输入的战术导弹末制导段无动力飞行作为研究对象,在领弹-从弹的编队构架下,首先基于导弹动力学建立了关于弹目二阶视线角的分布式非线性协同制导律设计模型;其次,基于滑模控制和干扰观测器设计了带有视线角约束的领弹对运动目标精确打击的制导律;第三,针对从弹提出了一种分布式非连续协同制导律,给出了其参数的自适应规律。同时给出了相关定理的数学证明以及仿真验证,证明了所设计制导律的有效性。
与已有的视线角协同制导律相比,本文所设计并使用的分布式滑模追踪算法可以对干扰进行有效的抑制,并能应用于舵偏控制下的动力学模型,更符合工程实际情况。

