可规定性能的自适应滑模制导律
付 昊,周波华,马萌晨
(1. 海装驻上海地区第六军事代表室,上海 201109; 2. 上海航天技术研究院,上海 201109; 3. 哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001)
0 引 言
近年来,随着高马赫数飞行器等先进武器的发展,针对高速大机动目标的制导律设计得到了越来越多的关注。制导律的设计是决定导弹性能好坏的关键。在一些作战场景中,可以通过特定的攻击角来增加导弹的作战效能[1-2]。KIM等基于传统的比例导引,通过附加时变偏置项来补偿目标的加速度信息和传感器噪声,设计了具有攻击角度约束的偏置比例制导律[3]。PARK等考虑到导引头视场角约束和导弹过载约束,设计了具有角度约束的比例制导律,并且分析了导弹在物理约束下的最大可实现攻击角度[4]。文献[5-7]设计了具有角度约束的最优制导律,将制导系统的攻击角约束问题转换为最优控制的约束问题。然而偏置比例导引和最优制导律主要是针对静止或低速移动目标。近几十年来,滑模控制理论由于其对外界干扰和系统参数不确定性具有较强的鲁棒性,在拦截机动目标的制导律设计中得到了广泛的应用。文献[8]针对机动目标,设计了具有攻击角度约束的滑模制导律。文献[9]设计了有限时间收敛的终端滑模制导律。文献[10]设计了非奇异终端滑模制导律来解决滑模面的奇异问题。
综合上述文献,虽然诸多学者对带有攻击角度约束的制导律进行了大量的研究,但大多数方法都只能保证末端的攻击角度约束,并不能限制视线角的收敛过程。某些作战场景需要对导弹的制导过程进行约束,如在导弹拦截隐身目标的情形中,由于目标的雷达反射面积通常在某一特定的位置易被识别,因此要求制导系统的视线角在末制导过程中快速收敛并保持在特定角度。在多导弹协同作战情形中,由于通信技术或协同探测的约束,要求多导弹之间的空间构型满足一定的约束,这也可以通过限制视线角收敛过程来实现。在预设性能控制方面,文献[11-12]提出了Funnel控制方法,该方法是自适应高增益控制方法的延续,用时变函数来代替单调递增的控制增益。当系统的输出误差接近性能边界时,Funnel控制方法调整出较高的控制增益值,从而保证满足约束条件。BECHLIOULIS和ROVITHAKIS提出了规定性能控制(prescribed perfarmance controller, PPC)理论。在设计的约束性能函数基础上,通过误差变换,将系统跟踪误差转化为等效的无约束系统,设计了PPC控制器[13]。针对高速大机动目标的拦截,本文设计了具有预设性能的自适应滑模制导律,具有形式简单、鲁棒性强等优点。
1 问题描述
1.1 期望的性能指标约束函数
考虑非线性控制系统形式如式(1)所示。
(1)
式中:x1、x2表示系统状态;u表示系统的控制输入;b为系统输入与状态变量间的转换系数;f为包含系统状态的变量;d表示系统的外界干扰。在非线性系统跟踪控制问题的研究中,一种典型的控制指标为在控制过程中设计控制输入u使得系统状态x1收敛到x1d,x2收敛到零并且收敛过程中系统状态的跟踪误差e=x1-x1d能够满足给定的指标约束。设期望的性能指标函数为λ(t),即控制目标转换为
(2)
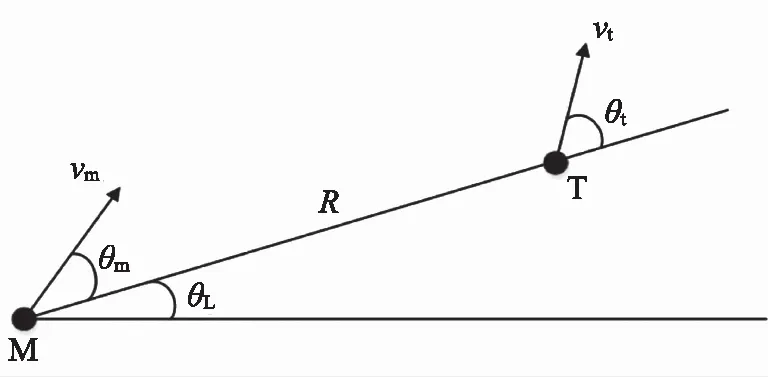
式中: 0 期望的性能约束函数设计为 λ(t)=(λ(0)-λ(∞))e-lt+λ(∞) (3) 式中:l为正常数;λ(0)为性能约束函数的初值;e(0)表示式(1)所示系统中的状态跟踪误差初值;λ(0)满足0<|e(0)|<λ(0),λ(∞)<λ(0),λ(∞)>0。 期望的性能约束过程如图1所示。 图1 期望的性能约束函数Fig.1 Desired performance constraint function 图1给出了期望的控制系统性能指标约束函数示意图。在控制系统的设计中,希望控制指标按规定的约束条件收敛。其中:l的值决定了性能约束函数收敛的速度,l越大,收敛速度越快;λ(∞)决定了性能约束函数稳态时的界;m表示跟踪误差的最大超调量。 设计中间函数为 (4) 式中:kh>0。 期望的性能约束过程可以表示为 (5) 由于0<|e(0)|<λ(0),且h(0)存在,故在定义域内可以对h(t)求导。 对h(t)求导可得 (6) 注1: 为了保证式(1)所示系统中的状态在收敛过程中系统误差能满足预设性能,由于h(0)存在,只需要确保系统在收敛过程中h(t)是有界的。 因此,我们将非线性系统跟踪控制问题中的状态约束转换为设计控制器,使得系统状态收敛过程中满足h(t)有界。 考虑二维平面内制导系统模型,如图2所示。 图2 二维制导系统示意图Fig.2 Guidance system in two-dimensional space 图2中:M表示导弹;T表示目标;R表示目标和导弹之间的相对距离;vm和vt分别表示导弹的速度和目标的速度,这里导弹和目标速度大小保持不变;θm和θt分别表示导弹速度和目标速度与视线之间的夹角;θL表示视线角;am表示导弹的法向加速度;at表示目标的法向加速度。这里以导弹作为坐标原点,则导弹目标的相对运动方程组为 (7) (8) (9) (10) (11) 为了方便制导律设计,给出下面的引理和假设。 (12) 式中:μ>0;λ>0和0<α<1是常数;x(t0)=x0,其中,t0是初始值。那么系统状态到达平衡点的时间ts满足 (13) 也就是说系统状态是有限时间收敛的。 1)V(x)为正定函数; 则系统为实际有效时间稳定的。 假设1:假设目标加速度at对于所有的t≥0是有界的并且满足|at|≤dmax,其中dmax是目标加速度的上界。 假设2[16]: 假设当R=R0≠0时导弹可成功拦截目标,R0属于区域[Rmin,Rmax]=[0.1 m,0.25 m]。 在满足性能指标约束的前提下,设计制导律使得系统能够以期望的角度拦截目标。令 设计滑模面S为 (16) 式中:k1,k2,k3和ρ均为正常数。对滑模面S进行求导可得 (17) 利用tanh(·)函数的有界性,设计能够保证函数h(t)有界的制导律。在满足假设1和假设2的情况下,如果目标干扰上界dmax已知,适用于拦截机动目标且具有性能指标约束的制导律设计为 (18) 式中:k4、k5为正常数,并且满足k5>ρk1dmax。 下面对非奇异制导律的稳定性进行证明。首先证明不等式(19)。 由假设1和双曲余弦函数cosh(·)的性质可得 (19) 选择李雅普诺夫函数V1为 (20) 对V1沿着式(7)~(10)所示的系统轨线求导,可得 (21) 将式(18)所示的控制器代入式(21),并结合不等式(19)可得 -k4S2-k5S·sign(S)+k1ρ|S|dmax≤ -k4S2-(k5-k1ρdmax)|S|≤ (22) 下面证明系统状态在滑模面S=0上的运动。 (23) 对V2求导可得 (24) 由h(t)>0和式(14)的性质可得 (25) 由李雅普诺夫稳定性理论可知,系统视线角误差渐近收敛到零,进而视线角速率渐近收敛到零。 注2:在以上的设计过程中,我们利用了tanh(·)函数的有界性,进而得到h(t)在系统收敛过程中始终有界,这意味着只要|e(0)|<λ(0),则整个系统收敛过程中始终满足性能约束条件。但在设计过程中,如果e(t)太过逼近λ(t),会导致h(t)较大,对控制器的控制性能要求较高,因此对控制器u中h(t)前面的参数k2不应选取过大。 注3:在假设1中,我们对系统的外部干扰做了假设,也就是|at| (26) (27) 下面对自适应滑模制导律的稳定性进行证明。选取李雅普诺夫函数V3为 (28) 对V3沿着式(7)~(10)所示的系统轨线求导,将式(17)和式(27)代入可得 -k4S2-k5|S|≤0 (29) 选择李雅普诺夫函数V4为 (30) 对V4求导可得 (31) 由于滑模面有限时间收敛到区域Δ,故由式(16)可得 (32) 式中,|Δ1|≤Δ。式(32)可以转化为 (33) 注4:由于存在符号函数,这在一定程度上会带来抖振现象。为了削弱该问题对闭环系统的影响,运用一个连续的饱和函数来近似符号函数,其具体形式为 (34) 式中,σ为一个小的正常数。 通过数值仿真来验证本文所设计的制导律的有效性。为了分析制导律的性能,目标的机动形式选择为蛇形机动at=5gcos(2t),其中,g=9.8 m/s2为重力加速度。 为了验证所设计制导律的性能,选择比例导引制导律(proportion navigation guidance law, PNGL)和之前设计的快速非奇异终端滑模制导律(fast nonsingular terminal sliding mode guidance law, FNTSMGL)[17-19]进行对比。PNGL的具体形式为 (35) 快速非奇异终端滑模的具体形式为 (36) (37) r1=(2-r)ηr-1 (38) r2=(r-1)ηr-2 (39) 式中,r、α1、α2和η都是待设计的正常数,0 对应的FNTSMGL形式为 (40) (41) 考虑两组不同的初始场景参数,具体如表1所示。 表1 导弹目标初始仿真条件Tab. 1 Initial simulation conditions for the missile and target 实际导弹的动力学执行机构的能力有限,即导弹所能提供的最大法向过载有限,具体形式为 其中,aM max=25g。 制导律u0中的参数选择为α1=0.02,α2=0.39,r=0.9,η=0.25,k1=6,k2=2。PNGL中的参数为N=5。 制导律u1参数选择为ρ=2.45,k1=0.5,k2=0.000 5,k3=1,k4=0.6,k5=2.7,饱和函数中的参数选择为σ=0.005,性能约束函数参数为λ(0)=12,λ(∞)=0.5,l=0.8,m=0.3,kh=0.01。 当at=5gcos(t)时,选择表1中的数据作为仿真初始参数,仿真结果如图3所示。由图3可知,3种制导律均能成功地拦截目标,但比例导引律不能保证视线角收敛,而制导律u1和u0均能保证导弹的视线角成功收敛到期望的视线角,且制导律u1能够使得视线角按期望性能指标进行收敛。u0和u1在制导开始阶段存在法向加速度饱和现象,这是因为选取的滑模面保证快速收敛的同时势必会造成较大的控制量,而比例导引因为有效导航比的选择产生的导弹法向加速度较小。 图3 制导律u1仿真图Fig. 3 Simulation under u1 考虑到实际目标有关参数并不容易精确得到,因此,开展自适应性能约束制导律设计。仿真初始参数选择表1中的第2组数据,制导律u2参数选择同u1:ρ=2.45,k1=0.5,k2=0.000 5,k3=1,k4=0.6,k5=2.7,自适应增益为δ=ρk1,饱和函数中的参数选择为σ=0.005,性能约束函数参数为λ(0)=12,λ(∞)=0.5,l=0.8,m=0.3,kh=0.01。仍选择比例制导律以及制导律u0与制导律u2进行对比,参数同上。 当at=5gcos(t)时,初始参数选择为表1中的数据,3种制导律下的仿真结果如图4所示,3种制导律均能成功地拦截目标,制导律u2和u0均能保证视线角成功地收敛到期望的视线角,且制导律u2亦能使视线角按期望性能指标进行收敛,这有利于进一步提高导弹的作战性能。 图4 目标蛇形机动下制导律u2仿真图Fig.4 Responses under u2 本文针对非线性系统中的性能约束问题,通过引入中间函数设计新的滑模面,将制导系统的视线角跟踪误差与期望的性能约束函数结合并引入到滑模面的设计中,通过滑模面的有界性设计了满足期望性能约束的制导律。本文所用方法的控制器形式简单,且具有较好的鲁棒性与实用性。仿真对比验证了本文所设计制导律的有效性和优越性。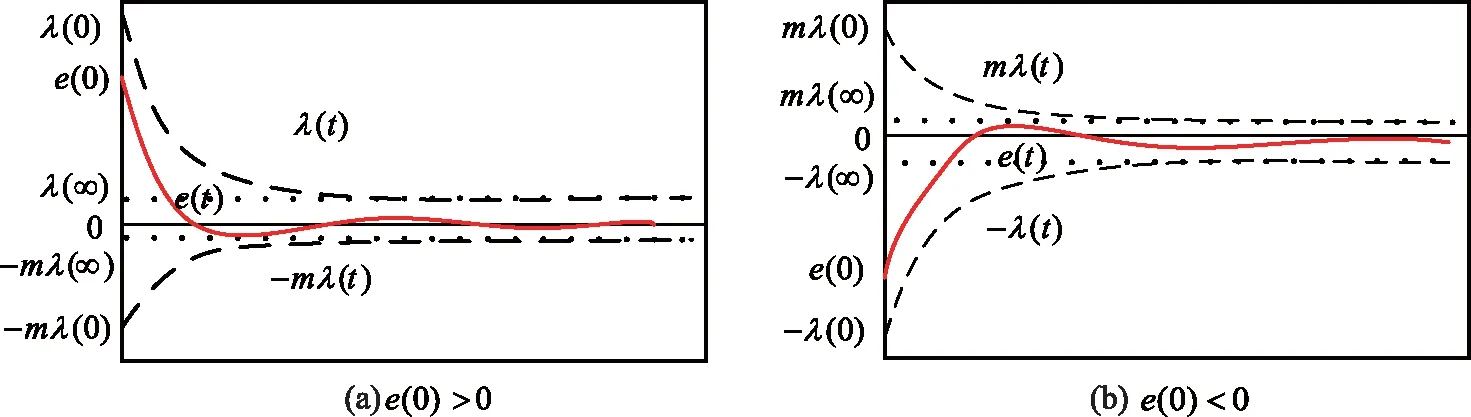
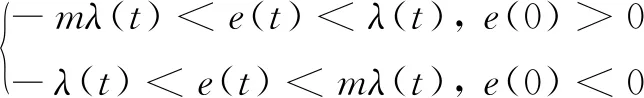
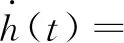
1.2 制导系统模型
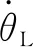

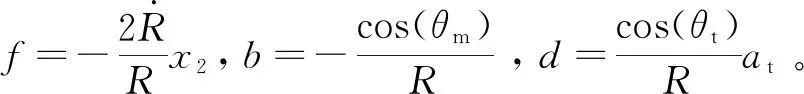
1.3 相关假设和引理
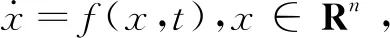
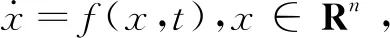
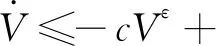
2 制导律设计
2.1 快速非奇异制导律设计
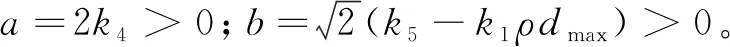
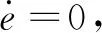

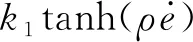
2.2 快速非奇异自适应制导律设计
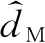
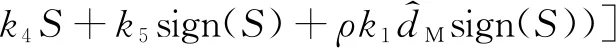
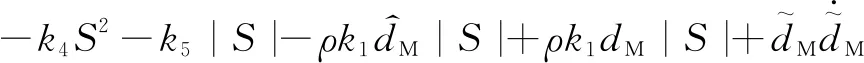
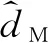
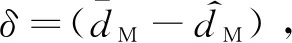

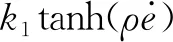
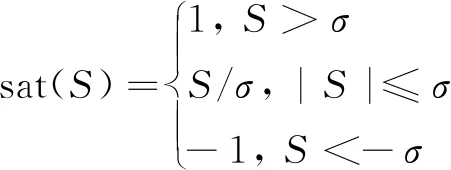
3 仿真验证

3.1 非奇异滑模制导律的仿真验证
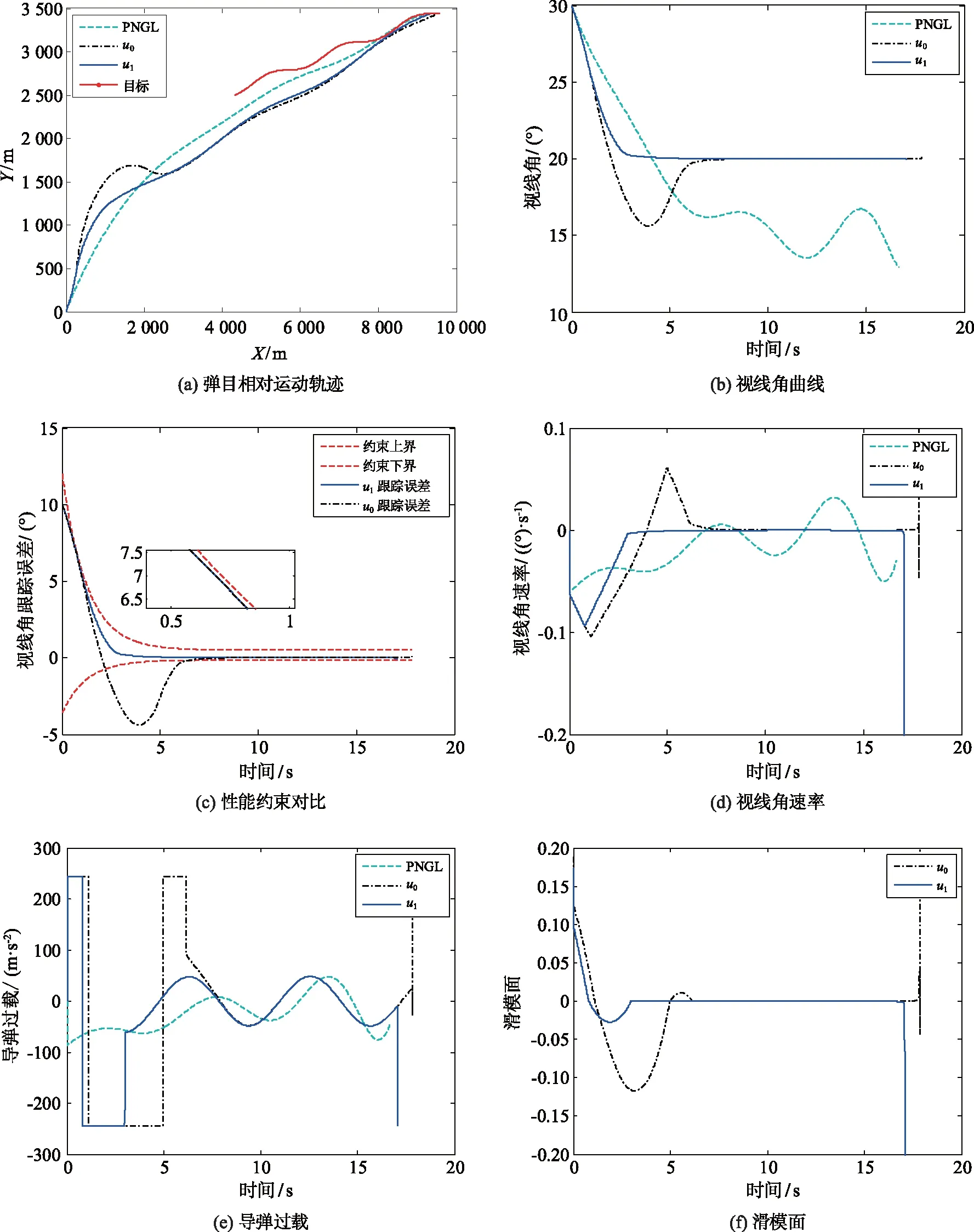
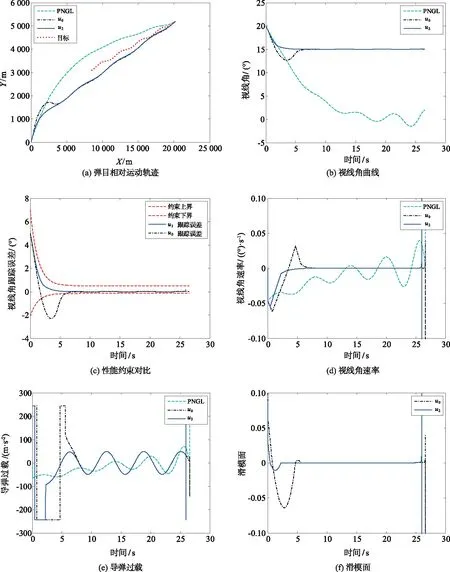
3.2 快速非奇异自适应制导律的仿真验证
4 结束语

